9 การรู้จำรูปแบบเชิงลำดับในโลกการประมวลผลภาษาธรรมชาติ

9.1 การประมวลผลภาษาธรรมชาติ

ภาษา หรือในบริษทของคอมพิวเตอร์ จะเรียกว่า ภาษาธรรมชาติ (natural language) เพื่อเน้นความแตกต่างจากภาษาโปรแกรม (programming language) ที่ใช้สำหรับเขียนโปรแกรมให้กับคอมพิวเตอร์. ภาษาธรรมชาติ เป็นภาษาที่คนใช้พูดสื่อสารกัน เช่น ภาษาไทย ภาษาจีน ภาษาสเปน ภาษาอังกฤษ. ภาษาธรรมชาติ ¹ มีการเกิด การพัฒนา การวิวัฒนาการตามธรรมชาติ. วิวัฒนการของภาษาเกิดจากคนจำนวนมาก และผ่านผู้คนหลายรุ่น แม้ว่าอาจมีบางครั้งที่ได้รับการควบคุม ปรับปรุง ผ่านกลุ่มคนจำนวนน้อย ๆ ที่มีอำนาจหรือที่ได้รับมอบหมายบ้าง. ส่วนภาษาโปรแกรม เป็นภาษาที่ออกแบบจากคนหรือกลุ่มคน (จำนวนไม่มาก) เพื่อใช้สั่งงานคอมพิวเตอร์. ตัวอย่างภาษาโปรแกรม เช่น ภาษาซี ภาษาซีพลัสพลัส ภาษาจาวา ภาษาอาร์ ภาษาไพธอน. ภาษาโปรแกรม จะมีไวยากรณ์ที่ตายตัว ใช้ควบคุมโครงสร้างของคำสั่งต่าง ๆ. ขณะที่ไวยากรณ์ของภาษาธรรมชาติ มักจะยืดหยุ่น และมีข้อยกเว้นอยู่มาก.

ไวยากรณ์ (syntax) คือกฎเกณฑ์ที่เกี่ยวกับโทเค็น และโครงสร้าง. โทเค็น (token) เป็นหน่วยพื้นฐานของภาษาที่มีความหมาย เช่น ในภาษาธรรมชาติ โทเค็น หมายถึง คำ. ในภาษาโปรแกรม โทเค็น หมายถึง คำ, ตัวแปร, ค่าตัวแปร, ค่าคงที่, นิพจน์, ฟังก์ชัน, ออปเจ็ค, เมท็อด เป็นต้น. โครงสร้างไวยากรณ์ คือการนำโทเค็นไปประกอบกันเพื่อสื่อความหมาย. ความสัมพันธ์ระหว่างโทเค็นและโครงสร้างไวยากรณ์ อาจแสดงได้ด้วยตัวอย่าง เช่น ในภาษาอังกฤษ “This 1s @ท Englisก s3nteทce.” มีการใช้โทเค็นที่ไม่ถูกต้อง. ส่วน “is.sentence ThisEnglish an” แม้จะใช้โทเค็นที่ถูกต้องทั้งหมด แต่เป็นการประกอบกันที่ไม่ถูกต้องตามไวยากรณ์ภาษาอังกฤษ. ประโยค “This is an English sentence.” ถูกไวยากรณ์ภาษาอังกฤษ (โทเค็นถูกต้องทั้งหมด และประกอบกันเป็นโครงสร้างที่ถูกต้อง). การวิเคราะห์โครงสร้างไวยากรณ์ของข้อความหรือประโยค จะเรียกว่า การแจกส่วน (parsing). เวลาที่เราอ่านข้อความต่าง ๆ เราทำการแจกส่วน เพื่อเข้าใจรูปประโยค ประกอบการทำเข้าใจความหมายของข้อความ.

นอกจากที่ภาษาโปรแกรมมีไวยากรณ์ที่ตายตัวมากกว่าภาษาธรรมชาติแล้ว ยังมีประเด็นที่แตกต่างกันดังนี้ (1) ความกำกวม (ambiguity) ที่ภาษาธรรมชาติมักอาศัยบริบทและสามัญสำนึกประกอบในการทำความเข้าใจข้อความ ในขณะที่ภาษาโปรแกรม ถูกออกแบบให้มีความชัดเจนโดยสมบูรณ์ ตีความได้อย่างเดียว ไม่มีความกำกวมเลย, (2) ความซ้ำซ้อน (redundancy) ที่พบได้บ่อย ๆ ในภาษาธรรมชาติ แต่ภาษาโปรแกรมจะกระชับและไม่ซ้ำซ้อน, (3) ความตรงตามตัวอักษร (literalness) ที่ภาษาโปรแกรมบอกความหมายที่เจาะจง ตรงตามตัวอักษร ในขณะที่ภาษาธรรมชาติ มีการใช้สำนวน โวหาร คำเปรียบเปรย.

ด้วยความแตกต่างระหว่างภาษาธรรมชาติและภาษาโปรแกรม ทำให้การประมวลผลภาษาธรรมชาติต้องการเครื่องมือ แนวทาง และกลไกเฉพาะ ที่นอกเหนือไปจากการยืมมาจากวิธีการต่าง ๆ ในการประมวลผลโปรแกรม.

การประมวลผลภาษาธรรมชาติ (Natural Language Processing คำย่อ NLP) เป็นศาสตร์ที่ใช้วิธีการต่าง ๆ เพื่อให้คอมพิวเตอร์สามารถนำข้อความในภาษาธรรมชาติไปประมวลผล และให้ผลลัพธ์ตามจุดประสงค์ของภาระกิจที่ต้องการ.

ภาระกิจของการประมวลผลภาษาธรรมชาตินั้นมีหลากหลายมาก เช่น ระบบตรวจสอบภาษา (spelling and grammar correction), ระบบช่วยจบคำอัตโนมัติ (autocompletion), ระบบตอบคำถามอัตโนมัติ (question answering system), การสรุปข้อความ (text summarization), แชทบอต (chatbot), การจำแนกอารมณ์ (sentiment classification), ระบบแปลภาษาอัตโนมัติ (machine translation), การค้นหาเนื้อหาในเอกสาร (content searching), การตรวจสอบการลอกเลียนวรรณกรรม (plagiarism detection) และการสร้างข้อความอัตโนมัติ (text generation). ลักษณะเฉพาะของภาษาเอง มีส่วนอย่างมากต่อความต้องการและความจำเป็นของภาระกิจต่าง ๆ เช่น ภาษาอังกฤษมีขอบเขตคำและขอบเขตประโยคที่ชัดเจน. การตัดคำ (word segmentation) และตัดประโยค (sentence segmentation) ในภาษาอังกฤษทำได้ง่ายมาก เมื่อเทียบกับภาษาไทย. ดังนั้นในขณะที่ ระบบอัตโนมัติสำหรับการตัดคำและการตัดประโยคในภาษาอังกฤษมีความสมบูรณ์เต็มที่และพร้อมใช้งาน ความสามารถของการตัดคำและการตัดประโยคอัตโนมัติในภาษาไทย กลับอยู่ในระดับเริ่มต้น และยังต้องการการพัฒนาอีกมาก. การตัดคำและการตัดประโยค นอกจากจะใช้ประกอบการจัดแสดงหน้าเอกสาร (ในการตัดคำขึ้นบรรทัดใหม่) การตัดคำและการตัดประโยค จัดเป็นภาระกิจพื้นฐานของการประมวลผลภาษาธรรมชาติ ที่จะช่วยให้งานที่มีความซับซ้อนอื่น ๆ สามารถประมวลผลต่อไปได้อย่างมีประสิทธิภาพ.

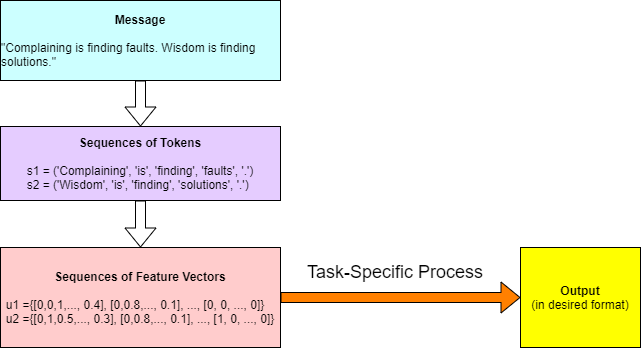
ภาพรวมของการประมวลผลภาษาธรรมชาติ โดยเฉพาะภาษาอังกฤษ ² คือ อินพุตที่ข้อความ จะถูกแปลงเป็นชุดลำดับของโทเค็น ซึ่งแต่ละโทเค็นเป็นคำ. จากนั้นแต่ละโทเค็น จะถูกแปลงเป็นเวกเตอร์ลักษณะสำคัญ ซึ่งเป็นเวกเตอร์ของค่าต่าง ๆ ที่เป็นตัวเลข ก่อนจะเข้ากระบวนการประมวลผลตามแต่ภาระกิจ. รูป 1.1 แสดงแนวทางการประมวลผลภาษาธรรมชาติ โดยทั่วไป ที่แปลงข้อความภาษาธรรมชาติ ไปเป็นชุดลำดับต่าง ๆ ของค่าเวกเตอร์ลักษณะสำคัญ ก่อนจะเข้าประมวลผล. แนวทางเช่นนี้ ทำให้สามารถใช้แบบจำลองเชิงลำดับต่าง ๆ ที่ทำงานกับข้อมูลที่มีค่าเป็นตัวเลข มาช่วยการประมวลผลตามแต่ภาระกิจได้.

รูป 1.2 แสดงลักษณะภารกิจการระบุหมวดคำ (Part-Of-Speech Tagging) ที่รับอินพุตเป็นข้อความ (ลำดับของคำ) แล้วให้เอาต์พุต ออกมาเป็นลำดับของหมวดคำ โดยลำดับของเอาต์พุตจะสอดคล้องกับลำดับของอินพุต. ในภาพ ข้อความอินพุตถูกแบ่งออกเป็นโทเค็น ซึ่ง ณ ที่นี้ แต่ละโทเค็นคือ คำ และเอาต์พุต ก็เป็นชุดลำดับข้อมูล ที่แต่ละจุดข้อมูลจะสอดคล้องกับแต่ละโทเค็น.

9.2 โครงข่ายประสาทเวียนกลับ

โครงข่ายประสาทเวียนกลับ (Recurrent Neural Network คำย่อ RNN) เป็นแบบจำลองโครงข่ายประสาทเทียม ที่อินพุตของแต่ละหน่วยย่อย นอกจากจะเป็นค่าของเอาต์พุตจากหน่วยย่อยในชั้นคำนวณก่อนหน้าแล้ว ยังสามารถเป็นค่าของเอาต์พุตของหน่วยย่อยในชั้นคำนวณเดียวกัน สำหรับจุดข้อมูลลำดับก่อนหน้าได้. เช่นเดียวกับการวิเคราะห์การคำนวณของโครงข่ายเป็นชั้นคำนวณ ดังอภิปรายในบทที่ [chapter: Convolution] โครงข่ายประสาทเวียนกลับ ก็สามารถมองเป็นการประกอบกันของชั้นคำนวณเวียนกลับ (recurrent layer) ได้.

การคำนวณของหน่วยย่อยในชั้นคำนวณเวียนกลับที่ \(q^{th}\) อาจเขียนได้ดังนี้ \[\begin{eqnarray} a_j^{(q)}(t) &=& \sum_{i=1}^D w_{ji}^{(q)} \cdot z_{i}^{(q-1)}(t) + \sum_{m=1}^M v_{jm}^{(q)} \cdot z_m^{(q)}(t-1) + b_j^{(q)} \label{eq: RNN feedforward a} \\ z_j^{(q)}(t) &=& h(a_j^{(q)}(t)) \label{eq: RNN feedforward z} \end{eqnarray}\] เมื่อ \(a_j^{(q)}(t)\) คือค่าตัวกระตุ้นของหน่วยย่อยที่ \(j^{th}\) สำหรับจุดข้อมูลลำดับที่ \(t^{th}\). ตัวแปร \(z_j^{(q)}(t)\) คือ ผลการ หรือบางครั้งอาจเรียก ว่าเป็น สถานะซ่อน ของหน่วยที่ \(j^{th}\) ในชั้นคำนวณ \(q^{th}\) สำหรับจุดข้อมูลลำดับเวลา \(t^{th}\) โดย \(D\) คือจำนวนหน่วยย่อยในชั้น \((q-1)^{th}\) และ \(M\) คือจำนวนหน่วยย่อยในชั้น \(q^{th}\). ตัวแปร \(w_{jd}^{(q)}\) เป็นค่าน้ำหนักของการเชื่อมต่อระหว่างหน่วยที่ \(d^{th}\) ของชั้น \((q-1)^{th}\) กับหน่วยที่ \(j^{th}\) ของชั้นคำนวณ \(q^{th}\). ตัวแปร \(v_{jm}^{(q)}\) เป็นค่าน้ำหนักของการเชื่อมต่อของหน่วยที่ \(m^{th}\) เวียนกลับมาเข้าหน่วยที่ \(j^{th}\) ของชั้นคำนวณเดียวกัน. ส่วน \(b_j^{(q)}\) คือค่าไบอัสของหน่วยที่ \(j^{th}\) และ \(h(\cdot)\) คือฟังก์ชันกระตุ้น.

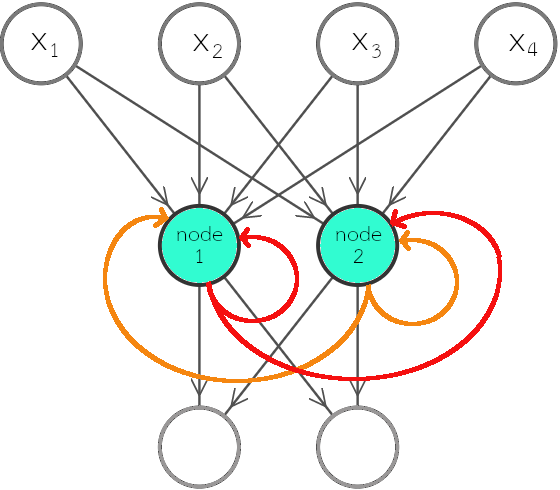
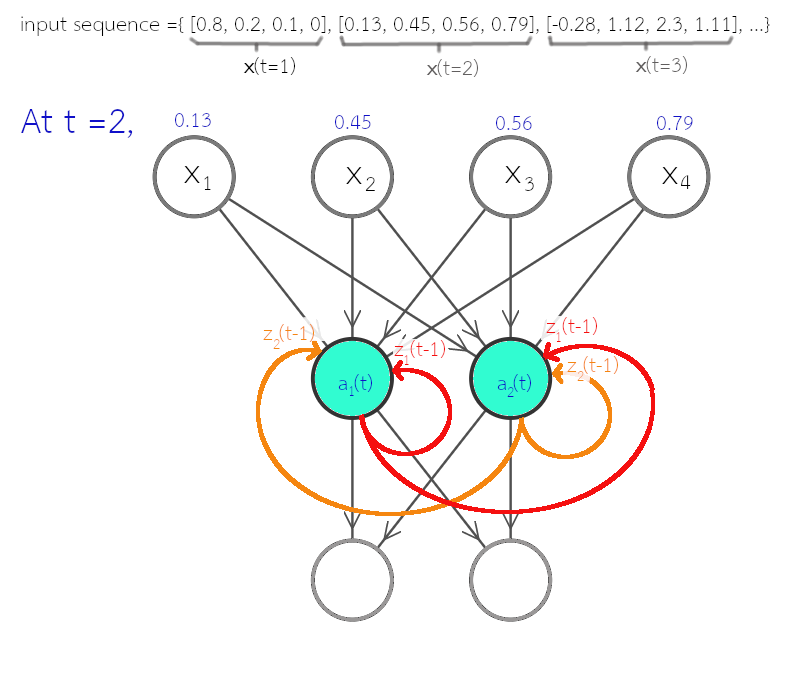
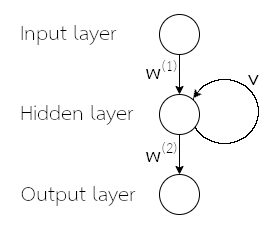
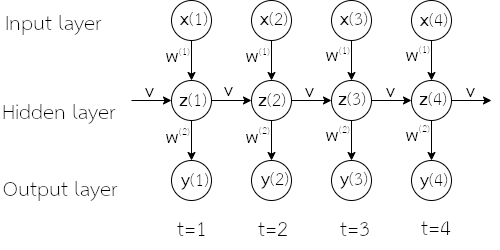
เมื่อเปรียบเทียบสมการ \(\eqref{eq: RNN feedforward a}\) กับสมการ \(\eqref{eq: mlp feedforward a}\) ซึ่งเป็นการคำนวณของโครงข่ายแพร่กระจายไปข้างหน้า จะเห็นว่าจุดต่างที่สำคัญ คือ พจน์ \(\sum_{m=1}^M v_{jm}^{(q)} \cdot z_m^{(q)}(t-1)\) ซึ่งเป็นการนำผลการกระตุ้นที่ลำดับเวลาก่อน เข้ามาคำนวณด้วย. รูป 1.3 แสดงตัวอย่างโครงสร้างการเชื่อมต่อของโครงข่ายประสาทเวียนกลับ ที่อินพุตมีสี่มิติ และเอาต์พุตมีสองมิติ โดยชั้นคำนวณที่สอง ซึ่งเป็นชั้นเวียนกลับ มีหน่วยย่อยสองหน่วย. รูป 1.4 แสดงตัวอย่างโครงข่ายประสาทเวียนกลับ พร้อมตัวอย่างชุดข้อมูลลำดับ และตัวแปรที่สำคัญ.

รูป 1.3 แสดงโครงข่ายประสาทเวียนกลับ โดยเน้นการแสดงโครงสร้าง. อย่างไรก็ตาม หากชั้นเวียนกลับมีจำนวนหน่วยมาก ๆ การเขียนแผนภาพเช่นนี้ จะดูยุ่งเหยิงมาก (แต่ละหน่วยส่งค่าเวียนกลับไปให้ทุก ๆ หน่วยในชั้น). บ่อยครั้ง แผนภาพโครงข่ายประสาทเวียนกลับ จึงม้ักถูกแสดงโดยใช้วงกลมแค่หนึ่งวงแทนชั้นคำนวณทั้งชั้น (ไม่ว่าภายในชั้นจะใช้จำนวนหน่วยเท่าใด) ดังแสดงในรูป 1.5. นอกจากนั้น ในบางสถานการณ์ การใช้แผนภาพคลี่ลำดับ (unfolding diagram) ที่แสดงข้อมูลการเวียนกลับ ด้วยการกระจายออกตามลำดับเวลา อาจช่วยให้เข้าใจแนวคิดได้ดีกว่า. แผนภาพคลี่ลำดับ อาจแสดงดังรูป 1.6.

จากแผนภาพคลี่ลำดับ ในรูป 1.6 สังเกต (1) ทุก ๆ ลำดับเวลา การคำนวณใช้ค่าน้ำหนักชุดเดียวกัน (ที่เวลา \(t\) ต่าง ๆ ใช้ค่า \(\boldsymbol{w}^{(1)}\), \(\boldsymbol{w}^{(2)}\) และ \(\boldsymbol{v}\) เหมือนกัน) (2) ผลการกระตุ้นของจุดข้อมูลลำดับเวลาใด ๆ \(\boldsymbol{z}(t)\) จะส่งผลต่อเอาต์พุตผ่านหลายเส้นทาง (เส้นทางตรง ส่งผลต่อ \(\boldsymbol{y}(t)\) และเส้นทางเวียนกลับเอาต์พุตอื่น ๆ หลังจากลำดับเวลานั้น ๆ ผ่านเส้นทางการเวียนกลับ).

9.3 โครงข่ายประสาทเวียนกลับสองทาง

โครงข่ายประสาทเวียนกลับ นำจุดข้อมูลลำดับก่อนหน้ามาร่วมพิจารณาผลการทำนายที่ลำดับเวลาปัจจุบัน ช่วยให้เราสามารถสร้างแบบจำลองความสัมพันธ์ของจุดข้อมูลลำดับปัจจุบัน กับจุดข้อมูลต่าง ๆ ในลำดับก่อนหน้าได้. อย่างไรก็ตาม ภารกิจกับข้อมูลเชิงลำดับหลายอย่าง อาจต้องการจำลองความสัมพันธ์ระหว่างจุดข้อมูลลำดับปัจจุบันกับจุดข้อมูลในลำดับหลัง ๆ เช่น กรณีภารกิจการระบุหมวดคำ ในรูป 1.2 การระบุหมวดคำของโทเค็น one ที่ถูกต้อง ต้องการรู้โทเค็นต่าง ๆ ที่ตามมาในภายหลัง นั่นคือ สำหรับ “... if one has the courage to admit them.” คำว่า “one” ทำหน้าที่เป็นสรรพนาม แต่ถ้าสำหรับ “... if one day you can let it go.” คำว่า “one” ทำหน้าที่เป็นตัวเลข. โครงข่ายประสาทเวียนกลับ ที่อาศัยเฉพาะแต่ความสัมพันธ์กับลำดับที่ผ่านมา ไม่อาจแก้ปัญหาลักษณะนี้ได้.

วิธีบรรเทาปัญหาลักษณะนี้อย่างง่าย ๆ ก็คือ การใช้กลไกหน้าต่างเวลา (time-window) ที่จับกลุ่มโทเค็นหลาย ๆ โทเค็นรวมกันเป็นจุดข้อมูลแต่ละจุด สำหรับโครงข่ายประสาทเวียนกลับ. อย่างไรก็ตาม แนวทางการใช้กลไกหน้าต่างเวลานี้ อาศัยกรอบหน้าต่างเวลา ที่มีความยาวคงที่ ทำให้จำกัดความสัมพันธ์ระยะยาวระหว่างจุดข้อมูล. อีกแนวทางง่าย ๆ ก็คือ การหน่วงเวลาระหว่างจุดข้อมูลลำดับของอินพุต กับจุดข้อมูลลำดับของเอาต์พุต แต่แนวทางนี้ ก็ยังต้องอาศัยการเลือกระยะเวลาหน่วงที่เหมาะสม.

แนวทางหนึ่ง ที่ถูกออกแบบและพบว่า ใช้ได้ดี สำหรับกรณีเช่นนี้ คือ โครงข่ายประสาทเวียนกลับสองทาง (bidirectional recurrent neural networks). กลไกที่สำคัญของโครงข่ายประสาทเวียนกลับสองทาง คือ เพิ่มชั้นคำนวณเวียนกลับที่รับชุดลำดับที่เรียงกลับหลัง. การคำนวณเอาต์พุตสุดท้ายของโครงข่าย จะรอจนกว่าชั้นคำนวณเวียนกลับ (ทั้งชั้นที่รับชุดลำดับเรียงหน้าไปหลัง และชั้นที่รับชุดลำดับเรียงหลังไปหน้า) จะได้ประมวลผลครบทุกจุดข้อมูลในชุดลำดับก่อน.

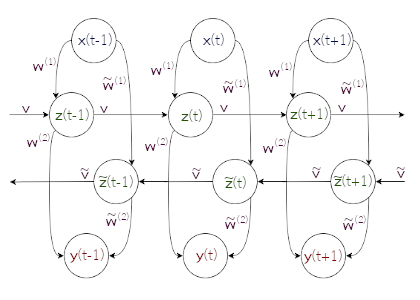
รูป 1.7 แสดงแผนภาพคลี่ลำดับของโครงข่ายประสาทเวียนกลับสองทาง. การคำนวณของหน่วยย่อยในชั้นคำนวณเวียนกลับทิศทางย้อนกลับที่ \(q^{th}\) อาจเขียนได้ดังนี้ \[\begin{eqnarray} \tilde{a}_j^{(q)}(t) &=& \sum_{i=1}^{\tilde{D}} \tilde{w}_{ji}^{(q)} \cdot \tilde{z}_{i}^{(q-1)}(t) + \sum_{m=1}^{\tilde{M}} \tilde{v}_{jm}^{(q)} \cdot \tilde{z}_m^{(q)}(t+1) + \tilde{b}_j^{(q)} \label{eq: BRNN backward direction layer a} \\ \tilde{z}_j^{(q)}(t) &=& h(\tilde{a}_j^{(q)}(t)) \label{eq: BRNN backward direction layer z} \end{eqnarray}\] เมื่อ \(\tilde{a}_j^{(q)}(t)\) และ \(\tilde{z}_j^{(q)}(t)\) คือ ค่าตัวกระตุ้นและผลการกระตุ้น ของหน่วยย่อยที่ \(j^{th}\) ในชั้นคำนวณ \(q^{th}\) สำหรับจุดข้อมูลลำดับที่ \(t^{th}\) โดย \(\tilde{D}\) คือจำนวนหน่วยย่อยในชั้น \((q-1)^{th}\) และ \(\tilde{M}\) คือจำนวนหน่วยย่อยในชั้น \(q^{th}\). ตัวแปร \(\tilde{w}_{jd}^{(q)}\) เป็นค่าน้ำหนักของการเชื่อมต่อระหว่างหน่วยที่ \(d^{th}\) ของชั้น \((q-1)^{th}\) กับหน่วยที่ \(j^{th}\) ของชั้นคำนวณ \(q^{th}\). ตัวแปร \(\tilde{v}_{jm}^{(q)}\) เป็นค่าน้ำหนักของการเชื่อมต่อของหน่วยที่ \(m^{th}\) เวียนกลับมาเข้าหน่วยที่ \(j^{th}\) ของชั้นคำนวณเดียวกัน, \(\tilde{b}_j^{(q)}\) คือค่าไบอัสของหน่วยที่ \(j^{th}\) และ \(h(\cdot)\) คือฟังก์ชันกระตุ้น.

สังเกตสมการ \(\eqref{eq: BRNN backward direction layer a}\) เปรียบเทียบกับสมการ \(\eqref{eq: RNN feedforward a}\) ซึ่งเป็นการคำนวณค่าตัวกระตุ้น ในชั้นคำนวณเวียนกลับ ทิศทางปกติ (ทิศทางไปข้างหน้า) จะเห็นว่า จุดสำคัญคือ การที่ค่าตัวกระตุ้น ในชั้นคำนวณเวียนกลับ ทิศทางย้อนกลับ ได้รับอิทธิพลจาก ผลการกระตุ้นของลำดับเวลาอนาคต \(\tilde{z}_m^{(q)}(t+1)\).

การคำนวณของหน่วยย่อยในชั้นรวมผลของทั้งสองทิศทาง (เช่น ชั้นเอาต์พุต ที่คำนวณค่า \(\boldsymbol{y}\) ในรูป 1.7) ก็สามารถดำเนินการได้ เช่นเดียวกับการคำนวณหน่วยย่อยในชั้นคำนวณเชื่อมต่อเต็มที่ทั่ว ๆ ไป นั่นคือ \[\begin{eqnarray} \hat{a}_j^{(q)}(t) &=& \sum_{i=1}^D w_{ji}^{(q)} \cdot z_{i}^{(q-1)}(t) + \sum_{i=1}^{\tilde{D}} \tilde{w}_{ji}^{(q)} \cdot \tilde{z}_{i}^{(q-1)}(t) + \hat{b}_j^{(q)} \label{eq: BRNN combine layer a} \\ \hat{z}_j^{(q)}(t) &=& h(\hat{a}_j^{(q)}(t)) \label{eq: BRNN combine layer z} \end{eqnarray}\] เมื่อ \(\hat{a}_j^{(q)}(t)\) และ \(\hat{z}_j^{(q)}(t)\) คือ ค่าตัวกระตุ้นและผลการกระตุ้น ของชั้นที่รวมผลจากการคำนวณเวียนกลับทั้งสองทิศทาง โดย \(z_{i}^{(q-1)}(t)\) และ \(\tilde{z}_{i}^{(q-1)}(t)\) คือผลการกระตุ้น จากชั้นเวียนกลับทิศทางไปข้างหน้า และทิศทางย้อนกลับ ตามลำดับ. ส่วน \(w_{ji}^{(q)}\), \(\tilde{w}_{ji}^{(q)}\) และ \(\hat{b}_j^{(q)}\) คือพารามิเตอร์ของชั้นคำนวณ.

เพื่อให้การคำนวณค่าเอาต์พุตของโครงข่ายประสาทเวียนกลับสองทาง เป็นไปโดยเรียบร้อย การคำนวณ (การแพร่กระจายไปข้างหน้า) ดำเนินการตามลำดับดังนี้

• คำนวณค่าผลการกระตุ้น จากชั้นเวียนกลับทิศทางไปข้างหน้า โดยคำนวณตามลำดับเวลาจาก \(t = 1\) ไป \(t = T\). นั่นคือ คำนวณค่า \(z_{i}^{(q-1)}(t)\) สำหรับ \(t = 1, \ldots, T\) ตามลำดับ.

• คำนวณค่าผลการกระตุ้น จากชั้นเวียนกลับทิศทางย้อนกลับ โดยคำนวณตามลำดับเวลาจาก \(t = T\) ไป \(t = 1\). นั่นคือ คำนวณค่า \(\tilde{z}_{i}^{(q-1)}(t)\) สำหรับ \(t = T, \ldots, 1\) ตามลำดับ.

• คำนวณชั้นที่รวมผลจากสองทิศทาง. นั่นคือ คำนวณค่า \(\hat{z}_j^{(q)}(t)\) สำหรับทุก ๆ ค่าของ \(t\) (ลำดับใดก็ได้).

การฝึกโครงข่ายประสาทเวียนกลับสองทาง ก็สามารถทำได้ในลักษณะเดียวกับการฝึกโครงข่ายประสาทเวียนกลับ เพียงมีความซับซ้อนเพิ่มขั้น เนื่องจาก (1) การเวียนกลับมีสองทิศทาง และ (2) การเวียนกลับทั้งสองทิศทาง เปรียบเสมือนส่วนประกอบในชั้นคำนวณเดียวกัน เพราะรับอินพุตจากชั้นเดียวกัน และให้เอาต์พุตออกไปที่ชั้นเดียวกัน.

การคำนวณในการฝึกชั้นเวียนกลับสองทาง (ชั้น \(q^{th}\)) สรุปได้ดังนี้

• (1) คำนวณการแพร่กระจายไปข้างหน้า

  • (1.0) คำนวนชั้น \((q-1)^{th}\)
    ได้ \(\hat{z}_i^{(q-1)}(t)\) สำหรับทุก ๆ \(i\) และทุก ๆ \(t\).
    ถ้าชั้น \((q-1)^{th}\) เป็นชั้นอินพุต \(\hat{z}_i^{(q-1)}(t) = x_i(t)\).

  • (1.1) คำนวณการเวียนกลับทิศทางไปข้างหน้า (\(t = 1, \ldots, T\) ตามลำดับ)
    ได้ \(a_j^{(q)}(t)\) และ \(z_j^{(q)}(t)\) สำหรับทุก ๆ \(j\) (สมการ \(\eqref{eq: RNN feedforward a}\) และ \(\eqref{eq: RNN feedforward z}\))

  • (1.2) คำนวณการเวียนกลับทิศทางกลับหลัง (\(t = T, \ldots, 1\) ตามลำดับ)
    ได้ \(\tilde{a}_j^{(q)}(t)\) และ \(\tilde{z}_j^{(q)}(t)\) สำหรับทุก ๆ \(j\) (สมการ \(\eqref{eq: BRNN backward direction layer a}\) และ \(\eqref{eq: BRNN backward direction layer z}\))

  • (1.3) คำนวณชั้น \((q+1)^{th}\)
    ได้ \(\hat{a}_k^{(q+1)}(t)\) และ \(\hat{z}_k^{(q+1)}(t)\) สำหรับทุก ๆ \(k\) และทุก ๆ \(t\).
    (สมการ \(\eqref{eq: BRNN combine layer a}\) และ \(\eqref{eq: BRNN combine layer z}\) ถ้าชั้น \((q+1)^{th}\) เป็นชั้นเชื่อมต่อเต็มที่)

  • คำนวณชั้นต่อ ๆ ไป จนได้เอาต์พุตสุดท้าย

• (2) คำนวณการแพร่กระจายย้อนกลับ

  • (2.0) คำนวณการแพร่กระจายย้อนกลับจนถึงชั้น \((q+1)^{th}\)
    ได้ \(\hat{\delta}_k^{(q+1)}(t) \equiv \frac{\partial E}{\partial \hat{a}_k^{(q+1)}(t)}\) สำหรับทุก ๆ \(k\) และทุก ๆ \(t\).

  • (2.1) คำนวณการแพร่กระจายย้อนกลับสำหรับทิศทางไปข้างหน้า (แต่การคำนวณต้องทำจาก \(t=T\) ไป \(t=1\))
    ได้ \(\delta_j^{(q)}(t)\), \(\frac{\partial E}{\partial w_{ji}^{(q)}}\), \(\frac{\partial E}{\partial v_{jm}^{(q)}}\) และ \(\frac{\partial E}{\partial b_j^{(q)}}\) สำหรับทุก ๆ \(i\), \(j\) และ \(m\) (สมการ \(\eqref{eq: RNN delta}\), \(\eqref{eq: RNN derivative dE/dw refined}\), \(\eqref{eq: RNN derivative dE/dv refined}\) และ \(\eqref{eq: RNN derivative dE/db}\))

  • (2.2) คำนวณการแพร่กระจายย้อนกลับสำหรับทิศทางกลับหลัง (การคำนวณต้องทำจาก \(t=1\) ไป \(t=T\))
    \[\begin{eqnarray} \tilde{\delta}_j^{(q)}(t) &\equiv& \frac{\partial E}{\partial \tilde{a}_j^{(q)}(t)} \nonumber \\ &=& h'(\tilde{a}_j^{(q)}(t)) \cdot \left(\sum_k \hat{\delta}_k^{(q+1)}(t) \cdot \tilde{w}_{kj}^{(q+1)} + \sum_m \tilde{\delta}_m^{(q)}(t-1) \cdot \tilde{v}_{mj}^{(q)}\right) \nonumber \\ \label{eq: BRNN backprop delta} \\ % \frac{\partial E}{\partial \tilde{w}_{ji}^{(q)}} &=& \sum_t \tilde{\delta}_j^{(q)}(t) \cdot \hat{z}_i^{(q-1)}(t) \label{eq: BRNN backprop dEw} \\ % \frac{\partial E}{\partial \tilde{v}_{jm}^{(q)}} &=& \sum_t \tilde{\delta}_j^{(q)}(t) \cdot \tilde{z}_m^{(q)}(t-1) \label{eq: BRNN backprop dEv} \\ \frac{\partial E}{\partial \tilde{b}_j^{(q)}} &=& \sum_t \tilde{\delta}_j^{(q)}(t) \label{eq: BRNN backprop dEb} \end{eqnarray}\] สำหรับทุก ๆ \(i\), \(j\) และ \(m\)

  • แพร่กระจายย้อนกลับต่อไปจนครบทุกชั้น
    ถ้าชั้น \((q-1)^{th}\) เป็นชั้นเชื่อมต่อเต็มที่ แล้ว \[\begin{eqnarray} \hat{\delta}_i^{(q-1)}(t) &\equiv& \frac{\partial E}{\partial \hat{a}_i^{(q-1)}(t)} \nonumber \\ &=& h'(\hat{a}_i^{(q-1)}(t)) \cdot \left(\sum_j \delta_j^{(q)}(t) \cdot w_{ji}^{(q)} + \sum_j \tilde{\delta}_j^{(q)}(t) \cdot \tilde{w}_{ji}^{(q)} \right) \nonumber \\ \label{eq: BRNN backprop previous delta}. \end{eqnarray}\]

• (3) ปรับค่าน้ำหนักตามเกรเดียนต์ที่คำนวณได้

โครงข่ายประสาทเวียนกลับสองทาง มีความสามารถในการเชื่อมความสัมพันธ์ ทั้งความสัมพันธ์กับลำดับในอดีต และลำดับในอนาคต. อย่างไรก็ตาม การใช้งานโครงข่ายประสาทเวียนกลับสองทาง เหมาะกับ (1) ลักษณะชุดข้อมูลที่ต้องการจำลองความสัมพันธ์กับลำดับในอนาคต และ (2) ภารกิจที่ต้องการเอาต์พุต หลังจากได้เห็นชุดข้อมูลครบทุกลำดับแล้ว. หากลักษณะชุดข้อมูลไม่ได้ต้องการความสัมพันธ์กับลำดับในอนาคต การคำนวณที่เพิ่มขึ้นของโครงข่ายประสาทเวียนกลับสองทาง จะกลายเป็นภาระที่ไม่จำเป็น. หากภารกิจต้องการเอาต์พุตก่อนที่แบบจำลองจะได้เห็นข้อมูลครบลำดับ โครงข่ายประสาทเวียนกลับสองทาง (ในรูปแบบดั้งเดิมนี้) จะไม่เหมาะสมกับภารกิจนั้น และอาจพิจารณาทางเลือกอื่น เช่น กลไกหน้าต่างเวลา หรือ การหน่วงเวลาระหว่างอินพุตและเอาต์พุต.

9.4 แบบจำลองความจำระยะสั้นที่ยาว

ดังข้อดีข้อเสียของโครงข่ายประสาทเวียนกลับ ที่ได้อภิปรายไปว่า โครงข่ายประสาทเวียนกลับ มีปัญหาการเลือนหายของเกรเดียนต์ ที่ทำให้โครงข่ายประสาทเวียนกลับ ไม่สามารถเชื่อมโยงความสัมพันธ์ระยะยาว (ความสัมพันธ์ระหว่างจุดข้อมูลที่ลำดับต่างกันมาก).

ปัญหาเรื่องนี้ นำไปสู่การพัฒนาวิธีแก้ต่าง ๆ มากมาย และหนึ่งในนั้น คือ แบบจำลองความจำระยะสั้นที่ยาว ที่ปัจจุบัน ได้รับการยอมรับอย่างกว้างขวาง.

แบบจำลองความจำระยะสั้นที่ยาว (long short-term memory model ที่มักย่อ LSTM) คือ โครงข่ายประสาทเวียนกลับ ที่เพิ่มกลไกควบคุมความจำค่าใหม่ ควบคุมการลืมค่าเก่า และควบคุมการระลึกความจำไปใช้ อย่างชัดเจน. รูป 1.8 แสดงโครงสร้างของแบบจำลองความจำระยะสั้นที่ยาว. แบบจำลองความจำระยะสั้นที่ยาว มีกลไกภายในหน่วยคำนวณย่อยที่ซับซ้อนกว่า หน่วยย่อยของโครงข่ายประสาทเทียมทั่วไปอยู่มาก ดังนั้น เพื่อกันการสับสน หน่วยคำนวณย่อยที่ครอบคลุมแนวคิดแบบจำลองความจำระยะสั้นที่ยาว จะเรียกว่า บล็อกความจำ (LSTM block). ภายในบล็อกความจำ มีหน่วยความจำ เรียก เซลล์ (cell) หรือเซลล์ความจำ (memory cell). กลไกการเก็บความจำของเซลล์นี้ คือ จุดเด่นของแบบจำลองความจำระยะสั้นที่ยาว ซึ่งบรรยายดังสมการ \(\eqref{eq: LSTM forget gate}\) ถึง \(\eqref{eq: LSTM cell output}\).

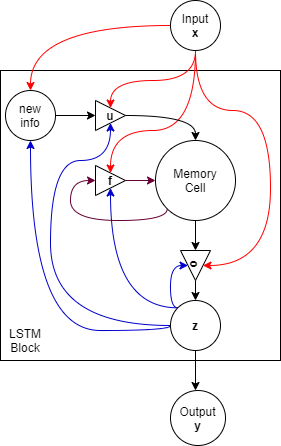
เมื่อ ชุดลำดับอินพุต คือ \([\boldsymbol{x}(1), \ldots, \boldsymbol{x}(T)]\) การคำนวณของบล็อกความจำ ดำเนินการดังนี้ \[\begin{eqnarray} \boldsymbol{f}(t) &=& \sigma(\boldsymbol{W}_f \cdot [\boldsymbol{z}(t-1); \boldsymbol{x}(t)] + \boldsymbol{b}_f) \label{eq: LSTM forget gate} \\ \boldsymbol{u}(t) &=& \sigma(\boldsymbol{W}_u \cdot [\boldsymbol{z}(t-1); \boldsymbol{x}(t)] + \boldsymbol{b}_u) \label{eq: LSTM input gate} \\ \boldsymbol{o}(t) &=& \sigma(\boldsymbol{W}_o \cdot [\boldsymbol{z}(t-1); \boldsymbol{x}(t)] + \boldsymbol{b}_o) \label{eq: LSTM output gate} \\ \tilde{\boldsymbol{c}}(t) &=& \mathrm{tanh}(\boldsymbol{W}_c \cdot [\boldsymbol{z}(t-1); \boldsymbol{x}(t)] + \boldsymbol{b}_c) \label{eq: LSTM new cell} \\ \boldsymbol{c}(t) &=& \boldsymbol{f}(t) \odot \boldsymbol{c}(t-1) + \boldsymbol{u}(t) \odot \tilde{c}(t) \label{eq: LSTM update cell} \\ \boldsymbol{z}(t) &=& \boldsymbol{o}_t \odot \mathrm{tanh}(\boldsymbol{c}(t)) \label{eq: LSTM cell output} \end{eqnarray}\] เมื่อ ตัวดำเนินการ \(\odot\) หมายถึง การคูณแบบตัวต่อตัว (element-wise product) และตัวดำเนินการ \([\;\cdot\; ; \;\cdot\;]\) หมายถึงการนำค่าเวคเตอร์ต่อกัน นั่นคือ ถ้า \(\boldsymbol{v}^{(1)} = [v^{(1)}_1, \ldots, v^{(1)}_M]^T\) และ \(\boldsymbol{v}^{(2)} = [v^{(2)}_1, \ldots, v^{(2)}_N]^T\) แล้ว \([\boldsymbol{v}^{(1)}; \boldsymbol{v}^{(2)}]\) \(= [v^{(1)}_1, \ldots, v^{(1)}_M, v^{(2)}_1, \ldots, v^{(2)}_N]^T\). ตัวแปร \(\boldsymbol{z}(t)\) เป็นผลลัพธ์ของบล็อค (สำหรับลำดับเวลา \(t\)).

ตัวแปร \(\boldsymbol{c}(t)\) ทำหน้าที่เป็นค่าความจำของเซลล์ ที่ลำดับเวลา \(t\). ส่วนตัวแปร \(\tilde{\boldsymbol{c}}(t)\) เป็นสารสนเทศใหม่ ที่ลำดับเวลา \(t\). ตัวแปร \(\boldsymbol{f}(t)\), \(\boldsymbol{u}(t)\) และ \(\boldsymbol{o}(t)\) ทำหน้าที่เป็นเสมือนประตูควบคุมการไหลของสารสนเทศ. ประตูลืม (forget gate) และประตูรับค่าใหม่ (update gate) ซึ่งคือ \(\boldsymbol{f}(t)\) และ \(\boldsymbol{u}(t)\) ตามลำดับ ควบคุมว่า จะให้เซลล์รับจำสารสนเทศใหม่ \(\tilde{\boldsymbol{c}}(t)\) หรือคงความจำเดิม \(\boldsymbol{c}(t-1)\). ประตูผลลัพธ์ (output gate) \(\boldsymbol{o}(t)\) ควบคุมว่า ควรจะระลึกความจำออกมาหรือไม่. ค่าอินพุต \(\boldsymbol{x}(t)\) และค่าผลลัพธ์ที่ผ่านมา \(\boldsymbol{z}(t-1)\) ควบคุมการทำงานของประตูต่าง ๆ. รูป 1.9 แสดงแผนภาพคลี่ลำดับของบล็อกความจำ.

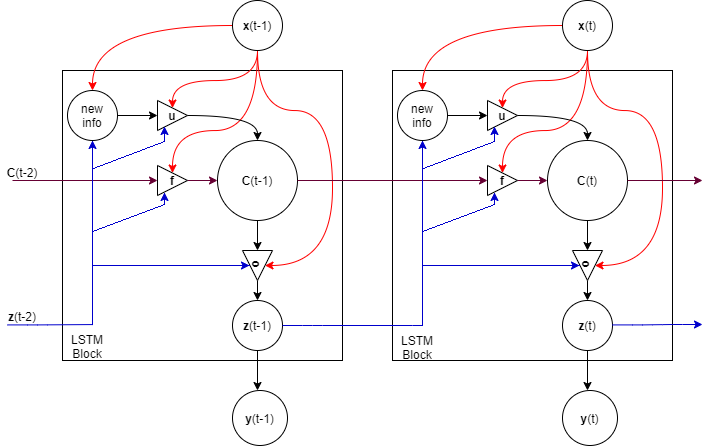
นอกจากนั้น เพืื่อปรับการควบคุมประตูได้แม่นยำยิ่งขึ้น โครงสร้างของบล็อกความจำ อาจมีกลไกช่องแอบมอง (peephole connections) เพิ่มเข้ามาด้วย. กลไกของช่องแอบมอง จะเพิ่มค่าของความจำที่ผ่านมา เข้ามาเป็นส่วนในการควบคุมประตูต่าง ๆ ด้วย ดังสมการ \(\eqref{eq: LSTM forget gate peephole}\) ถึง \(\eqref{eq: LSTM output gate peephole}\). \[\begin{eqnarray} \boldsymbol{f}(t) & = \sigma(\boldsymbol{W}_f \cdot [\boldsymbol{z}(t-1); \boldsymbol{x}(t); \boldsymbol{c}(t-1)] + \boldsymbol{b}_f) \label{eq: LSTM forget gate peephole} \\ \boldsymbol{u}(t) & = \sigma(\boldsymbol{W}_u \cdot [\boldsymbol{z}(t-1); \boldsymbol{x}(t); \boldsymbol{c}(t-1)] + \boldsymbol{b}_u) \label{eq: LSTM input gate peephole} \\ \boldsymbol{o}(t) & = \sigma(\boldsymbol{W}_o \cdot [\boldsymbol{z}(t-1); \boldsymbol{x}(t); \boldsymbol{c}(t-1)] + \boldsymbol{b}_o) \label{eq: LSTM output gate peephole}. \end{eqnarray}\]

9.5 การใช้งานโครงข่ายประสาทเวียนกลับ

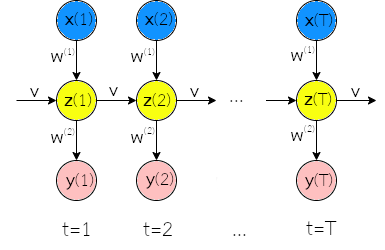
โครงข่ายประสาทเวียนกลับ ³ สามารถใช้เป็นแบบจำลองในการรู้จำรูปแบบเชิงลำดับแบบต่าง ๆ ดังอภิปรายในหัวข้อ [sec: seq data]. ตัวอย่างเช่น กรณีที่ทั้งอินพุตและเอาต์พุตเป็นชุดลำดับ และมีจำนวนลำดับเท่ากัน เช่น การระบุหมวดคำ (ดูแบบฝึกหัด [ex: nlp POS]) โครงข่ายประสาทเวียนกลับ สามารถนำมาใช้ในกรณีนี้ได้อย่างตรงไปตรงมา. กระบวนการฝึก อาจกำหนดให้ \(\mathcal{M}(t) = 1\) สำหรับทุก ๆ ลำดับเวลา \(t\). แผนภาพคลี่ลำดับ สำหรับกรณีนี้ แสดงในรูป 1.10.

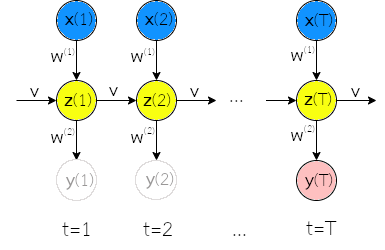
กรณีการจำแนกลำดับ เช่น การจำแนกอารมณ์ (ดูแบบฝึกหัด [ex: nlp sentiment analysis]) ที่อินพุตเป็นข้อมูลชุดลำดับ แต่เอาต์พุตไม่ได้เป็นชุดลำดับ นั่นคือ อินพุต \(\boldsymbol{X} =\{\boldsymbol{x}(1), \ldots, \boldsymbol{x}(T)\}\) และเอาต์พุต \(\boldsymbol{y}\). กรณีนี้อาจดำเนินการโดยกำหนดให้ ค่าทำนายที่ลำดับเวลาสุดท้าย เป็นเอาต์พุต และค่าทำนายต่าง ๆ ที่ลำดับเวลาอื่น ๆ ไม่มีความสำคัญ. กระบวนการฝึก ในกรณีการจำแนกลำดับ ก็สามารถทำได้สะดวก โดยการใช้กลไกหน้ากาก ที่กำหนดให้ \(\mathcal{M}(T) = 1\) และ \(\mathcal{M}(t \neq T) = 0\). รูป 1.11 แสดงแผนภาพคลี่ลำดับ สำหรับกรณีการจำแนกลำดับ.

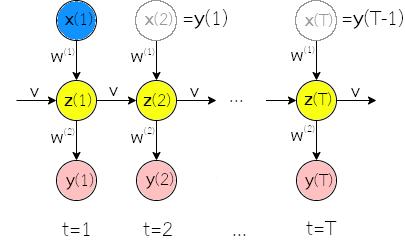
กรณีที่เอาต์พุตเป็นชุดลำดับ แต่อินพุตไม่ใช่ เช่น ระบบแต่งเพลงอัตโนมัติ (ดูแบบฝึกหัด [ex: seq music generation]) โครงข่ายประสาทเวียนกลับ ก็อาจสามารถนำมาประยุกต์ใช้ได้โดยจัดโครงสร้างดังแสดงในรูป 1.12. การจัดโครงสร้างที่นิยม สำหรับกรณีเช่นนี้ คือ ใช้อินพุตของระบบ เป็นอินพุตที่ลำดับเวลาแรกสุดของโครงข่ายประสาทเวียนกลับ และหลังจากนั้น ใช้เอาต์พุตที่คำนวณได้ มาเป็นอินพุตสำหรับลำดับเวลาถัดไป. การฝึกโครงข่ายประสาทเวียนกลับ สำหรับกรณีเช่นนี้ ซึ่งเป็นลักษณะของการใช้งานแบบจำลองก่อกำเนิด ก็สามารถใช้แนวทางของงานแบบจำลองก่อกำเนิด เช่น แนวทางของโครงข่ายปรปักษ์เชิงสร้างได้ (ดูหัวข้อ [sec: convapp fix enhance gen images] ประกอบ).

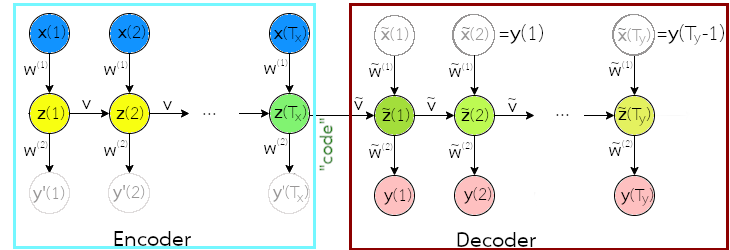
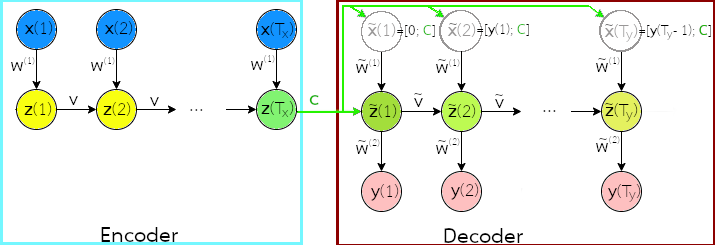
สุดท้าย กรณีที่ทั้งอินพุตและเอาต์พุตเป็นชุดลำดับ แต่มีจำนวนลำดับอาจไม่เท่ากัน เช่น ภารกิจการแปลภาษาอัตโนมัติ ที่จำนวนคำในประโยคของภาษาต้นทาง อาจไม่เท่ากับจำนวนคำในประโยคของภาษาเป้าหมาย. กรณีนี้ บ่อยครั้งอาจถูกอ้างถึงเป็น ภารกิจจำลองแบบชุดลำดับเป็นชุดลำดับ (sequence-to-sequence modeling task) เป็น สถานการณ์ที่ท้าทายอย่างมาก โดยเฉพาะ เมื่อการทำนายชุดลำดับของเอาต์พุต จำเป็นต้องเห็นอินพุตครบทุกลำดับก่อน. แนวทางหนึ่ง คือการใช้สถาปัตยกรรมตัวเข้ารหัสตัวถอดรหัส (encoder-decoder architecture) หรือบางครั้งอาจเรียก สถาปัตยกรรมแปลงชุดลำดับไปชุดลำดับ (sequence-to-sequence architecture) ดังแสดงในรูป 1.13 (ดูแบบฝึกหัด [ex: seq encoder-decoder configuration] เพิ่มเติม).

สถาปัตยกรรมตัวเข้ารหัสตัวถอดรหัส คล้ายการรวมแบบจำลองสองตัว. ตัวแรก สำหรับชุดลำดับอินพุต (เรียก ตัวเข้ารหัส) และตัวที่สอง สำหรับชุดลำดับเอาต์พุต (เรียก ตัวถอดรหัส). สถาปัตยกรรมตัวเข้ารหัสตัวถอดรหัส อาศัยกลไกของรหัสเนื้อความ (code) หรืออาจเรียก บริบท (context) ในการสรุปความหมายของชุดลำดับอินพุตไว้ แล้วค่อยถอดรหัสเนื้อความออกมาเป็นอีกชุดลำดับ.

โดยทั่วไป ผลการกระตุ้นลำดับสุดท้ายของตัวเข้ารหัส เช่น \(\boldsymbol{z}(T_x)\) ในรูป 1.13 จะถูกใช้เป็นรหัสเนื้อความ. ตัวถอดรหัส อาจรับรหัสเนื้อความ มาเป็นส่วนหนึ่งของผลการกระตุ้นเริ่มต้นของตัวถอดรหัส เช่น \(\tilde{\boldsymbol{z}}(0) = [\boldsymbol{z}(T_x); \boldsymbol{0}]\) โดย \(\boldsymbol{0}\) อาจเป็นค่าเริ่มต้นที่เติมเข้าไป เพื่อให้เต็มขนาด (ขนาดสถานะภายในของตัวถอดรหัส อาจใหญ่กว่าขนาดของรหัสเนื้อความได้). อินพุตลำดับแรกของตัวถอดรหัส \(\tilde{\boldsymbol{x}}(1)\) อาจกำหนดด้วยค่า \(\boldsymbol{0}\). ดูแบบฝึกหัด [ex: seq encoder-decoder configuration] เพิ่มเติม สำหรับการอภิปรายโครงสร้างของสถาปัตยกรรมตัวเข้ารหัสตัวถอดรหัสแบบอื่น.

โดยทั่วไป ขนาดสถานะภายในของตัวถอดรหัส ไม่เล็กกว่าขนาดสถานะภายในของตัวเข้ารหัส นั่นคือ \(|\boldsymbol{z}(t)| \leq |\tilde{\boldsymbol{z}}(t)|\). การกำหนดขนาดสถานะภายในของตัวถอดรหัส ให้ใหญ่กว่าขนาดรหัส ช่วยให้ตัวถอดรหัสเสมือนมีความจำเหลือพอที่จะใช้งานอื่น ๆ ได้ (เช่น อาจจะเก็บสถานะของการทำงาน ณ ลำดับเวลาปัจจุบัน).

แม้สถาปัตยกรรมตัวเข้ารหัสตัวถอดรหัส จะสามารถช่วยให้ชุดลำดับของเอาต์พุตมีจำนวนลำดับที่เป็นอิสระจากจำนวนลำดับของอินพุต และยังช่วยให้การทำนายชุดลำดับของเอาต์พุต ได้เห็นอินพุตครบทุกลำดับก่อน แต่สถาปัตยกรรมตัวเข้ารหัสตัวถอดรหัส ใช้กลไกของรหัส ในการส่งผ่านความหมายสรุปจากชุดลำดับอินพุต ไปสร้างชุดลำดับเอาต์พุต. ดังนั้น ขนาดของรหัส มีผลโดยตรงต่อความสามารถในการแทนความหมาย. ในกรณีของระบบการแปลภาษาอัตโนมัติ ขนาดของรหัสที่เล็กเกินไป จะส่งผลลบต่อคุณภาพการแปลอย่างชัดเจน โดยเฉพาะกับการแปลประโยคยาว ๆ (ดูแบบฝึกหัด [ex: seq encoder-decoder code length] เพิ่มเติม. หัวข้อ 1.6 อภิปรายกลไกความใส่ใจ ซึ่งพัฒนามาเพื่อแก้ข้อจำกัดนี้).

9.5.0.0.1 การจัดโครงสร้างเชิงลึกของโครงข่ายประสาทเวียนกลับ.

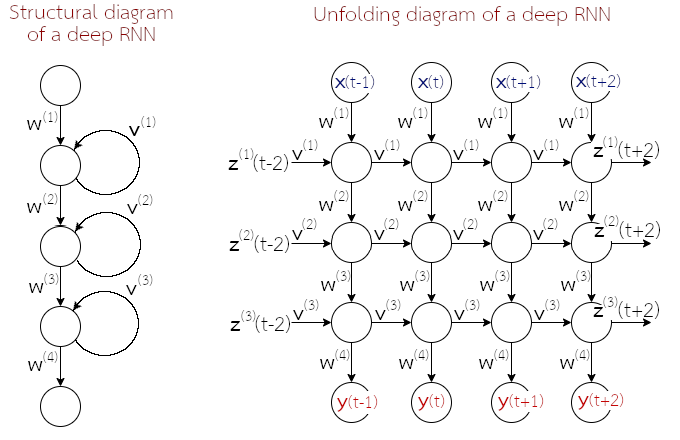
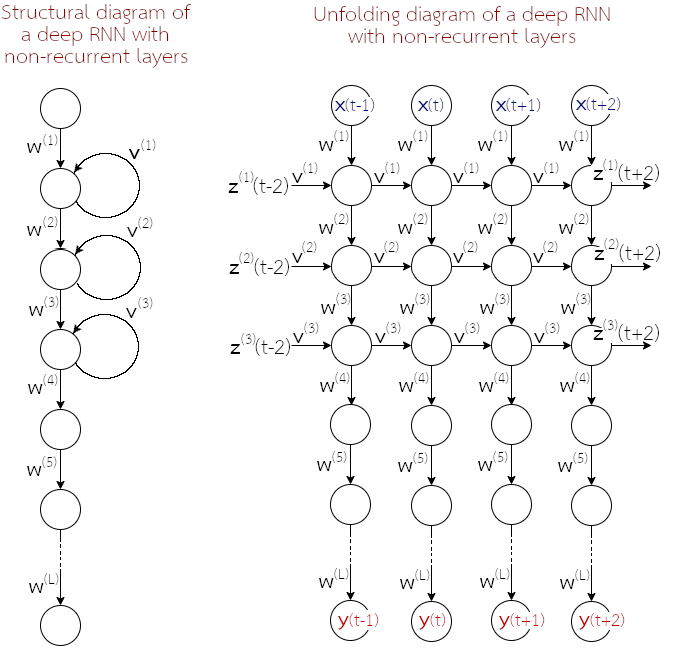
โครงข่ายประสาทเวียนกลับ (สมการ \(\eqref{eq: RNN feedforward a}\) และ  \(\eqref{eq: RNN feedforward z}\)) สามารถถูกจัดโครงสร้างแบบลึกได้ (รูป 1.14). อย่างไรก็ตาม ผู้เชี่ยวชาญศาสตร์การเรียนรู้ของเครื่อง แอนดรูว์ อึ้ง ให้ข้อสังเกตว่า แม้ปัจจุบัน โครงข่ายประเทียมเชิงลึกอาจมีจำนวนชั้นคำนวณเป็นหลักร้อยชั้นได้ (เช่น เรสเน็ต) แต่สำหรับโครงข่ายประสาทเวียนกลับ โดยเฉพาะชั้นคำนวณเวียนกลับ มักต่อกันไม่เกินสามชั้น ⁴ เหตุผลส่วนหนึ่ง อาจเป็นพราะกลไกการเวียนกลับได้เพิ่มความสามารถของแบบจำลองขึ้นอย่างมาก (รวมถึงเพิ่มความต้องการการคำนวณขึ้นอย่างมหาศาล โดยเฉพาะในกระบวนการฝึก). แต่โครงสร้างเชิงลึกมักพบ คือการใช้โครงข่ายประสาทเวียนกลับ ที่มีชั้นเวียนกลับ (หนึ่งถึงสามชั้น) แล้วต่อด้วยชั้นคำนวณ (ที่ไม่มีกลไกเวียนกลับ) หลาย ๆ ชั้น (รูป 1.15).

9.6 กลไกความใส่ใจ

สำหรับภารกิจจำลองแบบชุดลำดับเป็นชุดลำดับ เช่น การแปลภาษาอัตโนมัติ (machine translation), การสรุปข้อความ (text summarization), แชทบอต (chatbot) และระบบตอบคำถาม (question answering) สถาปัตยกรรมตัวเข้ารหัสตัวถอดรหัส สามารถทำงานได้ดี แต่ความสามารถของระบบลดลงอย่างมาก เมื่อชุดลำดับอินพุตมีความยาวมาก ๆ. คณะของบาห์ดาโน เชื่อว่าข้อจำกัดนี้ เกิดจากปัญหาคอขวดที่การใช้รหัสเนื้อความ ซึ่งมีความยาวจำกัด และได้เสนอวิธีการแก้ด้วยกลไกความใส่ใจ.

แนวคิดของกลไกความใส่ใจ พัฒนาจากภารกิจการแปลภาษาอัตโนมัติ ซึ่งสังเกตว่า เวลาที่คนแปลภาษา แม้จะเป็นการแปลจากประโยคยาว ๆ ในภาษาต้นทาง แต่เวลาแปล ถอดความออกมาเป็นคำ ๆ ในภาษาปลายทาง ผู้แปล แม้จะเห็นทั้งประโยค แต่เวลาพิจารณาเลือกคำ แต่ละคำ ที่จะใช้สำหรับประโยคปลายทาง ผู้แปลจะใส่ใจกับเฉพาะบางส่วนของประโยคต้นทางเท่านั้น.

ตัวอย่างเช่น ประโยคต้นทาง (ภาษาอังกฤษ) คือ “Knowing that what is cannot be undone—because it already is — you say yes to what is or accept what isn’t.” ⁵
ประโยคปลายทาง (ภาษาไทย) คือ “การรู้ว่า สิ่งที่เป็น ไม่สามารถเปลี่ยนแปลงได้ (เพราะว่ามันเป็นไปแล้ว) คุณยอมรับกับ สิ่งที่เป็น หรือยอมรับ สิ่งที่ไม่ได้เป็น.”

เอาต์พุต “การรู้ว่า” อาจมาจากโทเค็น “Knowing” และโทเค็น “that” เป็นหลัก โดยส่วนอื่น ๆ ของประโยคต้นทางมีความเกี่ยวข้องต่ำ.

9.6.0.0.1 การทำงานของกลไกความใส่ใจ.

แทนที่จะอาศัยการส่งเนื้อความจากชุดลำดับอินพุต ไปชุดลำดับเอาต์พุต ผ่านรหัสเนื้อความที่มีความยาวจำกัด และให้อิสระกับตัวถอดรหัสในการจัดเรียงเอาต์พุตเอง กลไกความใส่ใจ (attention mechanism) กำหนดบริบทสำหรับแต่ละลำดับ ให้กับตัวถอดรหัสโดยตรง.

ด้วยชุดลำดับอินพุต \(\boldsymbol{X} = [\boldsymbol{x}(1), \ldots, \boldsymbol{x}(T_x)]\) สถาปัตยกรรมตัวเข้ารหัสตัวถอดรหัส คำนวณรหัสเนื้อความ \[\begin{eqnarray} \boldsymbol{c} = e'(\boldsymbol{z}(1), \ldots, \boldsymbol{z}(T_x)) \label{eq: encoder-decoder encoding context} \end{eqnarray}\] เมื่อ \[\begin{eqnarray} \boldsymbol{z}(t) = e(\boldsymbol{z}(t-1), \boldsymbol{x}(t), \boldsymbol{z}(t+1)) \label{eq: encoder-decoder encoding hidden states} \end{eqnarray}\] โดย \(e'(\cdot)\) และ \(e(\cdot)\) เป็นฟังก์ชันของตัวเข้ารหัส ที่ทำหน้าที่สรุป และจำลองแบบเชิงลำดับ. ตัวอย่างเช่น \(e'(\boldsymbol{z}(1), \ldots, \boldsymbol{z}(T_x)) = \boldsymbol{z}(T_x)\) และ \(e(\cdot)\) เป็นโครงข่ายประสาทเวียนกลับสองทาง.

ในสถาปัตยกรรมตัวเข้ารหัสตัวถอดรหัสแบบดั่งเดิม (รูป 1.16) ตัวถอดรหัสรับรหัสเนื้อความ \(\boldsymbol{c}\) และระบบประมาณความน่าจะเป็นของเอาต์พุตที่ลำดับ \(t\) ด้วย \[\begin{eqnarray} p(\boldsymbol{y}(t) | \{\boldsymbol{y}(1), \ldots, \boldsymbol{y}(t-1)\}, \boldsymbol{X}) \approx \mathcal{D}(\boldsymbol{y}(t-1), \tilde{\boldsymbol{z}}(t), \boldsymbol{c}) \label{eq: encoder-decoder decoding context} \end{eqnarray}\] เมื่อ \(\mathcal{D}(\cdot)\) เป็นฟังก์ชันที่อนุมานความน่าจะเป็นของเอาต์พุต ⁶ และ \(\tilde{\boldsymbol{z}}(t)\) เป็นสถานะซ่อน ของโครงข่ายประสาทเวียนกลับ ที่ลำดับเวลา \(t\).

จากสมการ \(\eqref{eq: encoder-decoder decoding context}\) เราจะเห็นว่า ตัวถอดรหัสรับรู้ชุดลำดับอินพุต \(\boldsymbol{X}\) ผ่านรหัสเนื้อความ \(\boldsymbol{c}\) ตลอดการประมาณเอาต์พุตทุก ๆ ลำดับ. ดังนั้น ชุดลำดับอินพุตที่มีความยาวมาก อาจจะยัดเยียดสารสนเทศจำนวนมากลงไปในรหัสเนื้อความ \(\boldsymbol{c}\) ซึ่งแม้โดยแนวคิด รหัสเนื้อความไม่ได้ถูกจำกัดขนาด แต่ในทางปฏิบัติ การนำแนวคิดสถาปัตยกรรมตัวเข้ารหัสตัวถอดรหัสไปใช้งาน จะกำหนดขนาดของรหัสเนื้อความนี้ และขนาดของรหัสเนื้อความที่จำกัด อาจทำให้เกิดปัญหาคอขวดกับชุดลำดับยาว ๆ ได้.

กลไกความใส่ใจ เสนอใช้บริบทตามตำแหน่งลำดับ แทนที่จะใช้รหัสเนื้อความเดียวกันทุก ๆ ลำดับ. นั่นคือ ตัวถอดรหัส ประมาณความน่าจะเป็นของเอาต์พุตที่ลำดับ \(t\) ด้วย \[\begin{eqnarray} p\left(\boldsymbol{y}(t) | \{\boldsymbol{y}(1), \ldots, \boldsymbol{y}(t-1)\}, \boldsymbol{X}\right) \approx \mathcal{D}\left(\boldsymbol{y}(t-1), \tilde{\boldsymbol{z}}(t), \boldsymbol{c}_t\right) \label{eq: attention decoding context} \end{eqnarray}\] โดย \(\boldsymbol{c}_t\) เป็นบริบทสำหรับเอาต์พุตที่ลำดับเวลา \(t\). ค่าสถานะซ่อนคำนวณได้จาก \[\begin{eqnarray} \tilde{\boldsymbol{z}}(t) &=& d(\tilde{\boldsymbol{z}}(t-1), \boldsymbol{y}(t-1), \boldsymbol{c}_t) \label{eq: attention decoder z} \end{eqnarray}\] เมื่อ \(d(\cdot)\) เป็นส่วนของตัวถอดรหัสที่ทำหน้าที่จำลองแบบเชิงลำดับ ⁷ .

บริบท \(\boldsymbol{c}_t\) ควรจะขึ้นกับชุดลำดับของเนื้อความย่อย \(\{\boldsymbol{z}(1), \ldots, \boldsymbol{z}(T_x)\}\) ที่ตัวเข้ารหัสได้วิเคราะห์มาจากชุดลำดับอินพุต. เนื่องจากตัวเข้ารหัสเป็นโครงข่ายประสาทเวียนกลับสองทาง แต่ละเนื้อความย่อย \(\boldsymbol{z}(t)\) จึงถูกสรุปมาจากอินพุตทั้งชุดลำดับ โดยเน้นลำดับต่าง ๆ บริเวณรอบ ๆ ลำดับ \(t\) (ของชุดลำดับอินพุต).

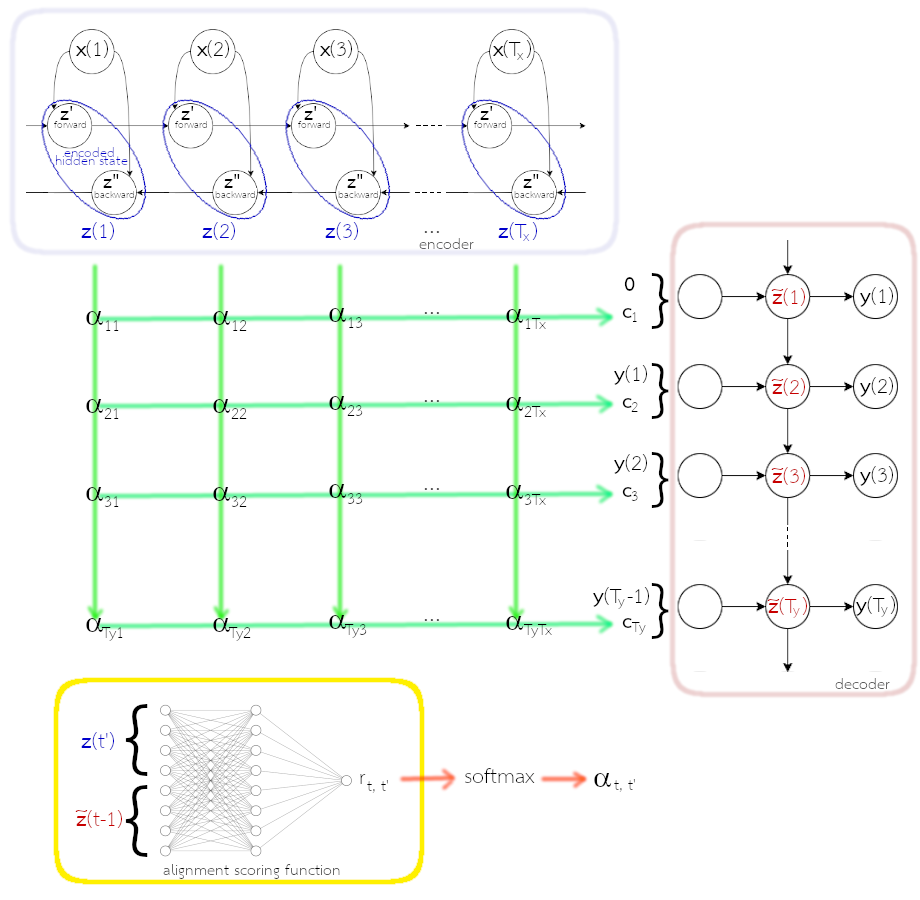
คณะของบาห์ดาโน กำหนดให้บริบทของเอาต์พุตที่ลำดับเวลา \(t\) เป็นผลรวมตามน้ำหนักของเนื้อความย่อยต่าง ๆ. นั่นคือ \[\begin{eqnarray} \boldsymbol{c}_t &=& \sum_{t'=1}^{T_x} \alpha_{t,t'} \cdot \boldsymbol{z}(t') \label{eq: attention context} \end{eqnarray}\] โดย \(\alpha_{t,t'}\) เรียกว่า ค่าน้ำหนักความใส่ใจ (attention weight) เป็นค่าน้ำหนักที่ระบุการจัดตำแหน่งแบบอ่อน ๆ (soft alignment) ของลำดับเอาต์พุต เทียบกับลำดับอินพุต. และเพื่อให้การคำนวณมีเสถียรภาพ ค่าน้ำหนักความใส่ใจ \(\alpha_{t,t'}\) จะถูกควบคุมให้ \(0 \leq \alpha_{t,t'} \leq 1\) สำหรับทุก ๆ \(t\) และ \(t'\) และ \(\sum_{t'} \alpha_{t,t'} = 1\) ด้วยฟังก์ชันซอฟต์แมกซ์ \[\begin{eqnarray} \alpha_{t,t'} &=& \frac{\exp(r_{t,t'})}{\sum_{\tau=1}^{T_x} \exp(r_{t,\tau})} \label{eq: attention attention weights} \end{eqnarray}\] เมื่อ \(r_{t,t'}\) เป็นแบบจำลองการจัดเรียงตำแหน่ง (alignment model) ที่ระบุคะแนนว่าอินพุตลำดับ \(t'\) ควรมีผลกับเอาต์พุตลำดับ \(t\) มากน้อยขนาดไหน. แบบจำลองการจัดเรียงตำแหน่ง ควรขึ้นอยู่กับสถานะซ่อนจากคู่ลำดับอินพุตและเอาต์พุต ดังนั้น \[\begin{eqnarray} r_{t,t'} &=& f(\tilde{\boldsymbol{z}}(t-1), \boldsymbol{z}(t')) \label{eq: attention attention scores} \end{eqnarray}\] โดย \(f(\cdot)\) เป็นฟังก์ชันคำนวณคะแนนความสัมพันธ์ระหว่างลำดับ \(t'\) ของอินพุต กับลำดับ \(t\) ของเอาต์พุต. สมการ \(\eqref{eq: attention attention scores}\) ใช้ \(\tilde{\boldsymbol{z}}(t-1)\) แทนที่จะเป็น \(\tilde{\boldsymbol{z}}(t)\) เพราะว่า \(\tilde{\boldsymbol{z}}(t-1)\) คือสถานะซ่อนล่าสุดของตัวถอดรหัส (ดูลำดับการคำนวณประกอบ). ฟังก์ชันคะแนน \(f(\cdot)\) ก็สามารถทำได้จากโครงข่ายประสาทเทียม โดยทำการฝึกโครงข่ายไปพร้อม ๆ กับแบบจำลองส่วนอื่น ๆ ของระบบ.

สังเกต ฟังก์ชัน \(f(\cdot)\) คำนวณคะแนน โดยใช้ค่าเวคเตอร์จากสถานะซ่อน ไม่ได้ใช้ค่าดัชนี \(t\) หรือ \(t'\) โดยตรง. ดังนั้น (1) ไม่ต้องกังวลเรื่องความยาวของลำดับ และ (2) การเชื่อมโยงระหว่างลำดับอินพุต และลำดับเอาต์พุต ทำผ่านสถานะซ่อน ไม่ได้ขึ้นกับตำแหน่งสัมบูรณ์.

รูป 1.17 แสดงโครงสร้าง เมื่อใช้กลไกความใส่ใจ. สถานะซ่อนของตัวเข้ารหัสทุก ๆ ลำดับเวลา จะถูกนำไปประกอบเป็นบริบท โดยสถานะซ่อนที่ลำดับเวลาใด จะถูกผสมเข้าไปมากน้อยเท่าไร ขึ้นกับน้ำหนักความใส่ใจ. สถานะซ่อนของตัวเข้ารหัส \(\boldsymbol{z}(t) = [\boldsymbol{z}'(t); \boldsymbol{z}''(t)]\) เมื่อ \(\boldsymbol{z}'(t)\) และ \(\boldsymbol{z}''(t)\) คือ ผลกระตุ้นในทิศทางไปข้างหน้า และกลับหลัง ตามลำดับ.

ด้วยกลไกความใส่ใจ ไม่ว่าชุดลำดับอินพุตจะยาวเท่าไร แต่ละลำดับเวลาของเอาต์พุต จะเสมือนมองเห็นทั้งชุดลำดับอินพุต เพียงแต่เน้นความหมายจากเฉพาะส่วนที่เกี่ยวข้องเท่านั้น ซึ่งแม้ขนาดของบริบทที่ลำดับ \(\boldsymbol{c}_t\) จะไม่ได้ใหญ่ไปกว่าขนาดของรหัสเนื้อความ \(\boldsymbol{c}\) แต่การที่ค่าของบริบทเปลี่ยนไปตามลำดับของเอาต์พุตได้ ช่วยแก้ปัญหาคอขวดของภารกิจจำลองแบบชุดลำดับเป็นชุดลำดับได้อย่างดี. ปัจจุบัน กลไกความใส่ใจ เป็นศาสตร์และศิลป์ของการเรียนรู้เชิงลึก โดยเฉพาะภารกิจเกี่ยวกับการประมวลผลภาษาธรรมชาติ มีการประยุกต์ใช้อย่างกว้างขวาง (รวมถึงภารกิจนอกเหนือจากงานประมวลผลภาษาธรรมชาติทั่วไปด้วย เช่น ) และเป็นแรงบันดาลใจให้เกิดการพัฒนาอย่างต่อเนื่อง จนเป็นแนวทางของตัวแปลง (transformer).

9.7 อภิธานศัพท์

โครงข่ายประสาทเวียนกลับ (Recurrent Neural Network คำย่อ RNN):

โครงข่ายประสาทเทียม ที่โครงสร้างการคำนวณมีการเชื่อมต่อ ที่นำค่าที่คำนวณแล้วในลำดับเวลาก่อนกลับเข้ามาคำนวณในลำดับเวลาปัจจุบันด้วย.

แผนภาพคลี่ลำดับ (unfolding diagram):

แผนภาพโครงสร้างของโครงข่ายประสาทเทียม ที่กระจายการแสดงการเวียนกลับเชิงลำดับเวลา ออกเป็นลักษณะเดียวกับโครงสร้างตรรกะกายภาพ. แผนภาพคลี่ลำดับ นิยมใช้แสดงการเชื่อมต่อของโครงข่ายประสาทเวียนกลับ.

การแพร่กระจายย้อนกลับผ่านเวลา (backpropagation through time คำย่อ BPTT):

ขั้นตอนวิธีการคำนวณเกรเดียนต์ สำหรับโครงข่ายประสาทเวียนกลับ.

ปัญหาการระเบิดของเกรเดียนต์ (exploding gradient problem):

ปัญหาที่อาจพบกับการฝึกโครงข่ายประสาทเวียนกลับ ที่เกรเดียนต์มีค่าเพิ่มขั้นอย่างมาก เมื่อเวียนกลับย้อนลำดับเวลา.

การเล็มเกรเดียนต์ (gradient clipping):

วิธีแก้ปัญหาการระเบิดของเกรเดียนต์ ด้วยวิธีจำกัดขนาดของ ที่จะใช้คำนวณปรับค่าน้ำหนัก.

โครงข่ายประสาทเวียนกลับสองทาง (bidirectional recurrent neural network คำย่อ BRNN):

โครงข่ายประสาทเวียนกลับ ที่ใช้นำค่าสถานะทั้งในลำดับก่อนหน้า (ทิศทางปกติ) และลำดับหลัง (ทิศทางย้อนกลับ) เวียนมาคำนวณผลลัพธ์ในลำดับปัจจุบัน.

แบบจำลองความจำระยะสั้นที่ยาว (long short-term memory model คำย่อ LSTM):

แบบจำลอง โครงข่ายประสาทเวียนกลับ ที่มีการใช้กลไกของประตูควบคุมการปรับเปลี่ยนค่าสถานะและค่าผลลัพธ์ของหน่วยคำนวณ เพื่อช่วยเพิ่มประสิทธิผลในการรู้จำความสัมพันธ์ระยะยาวของข้อมูล.

ช่องแอบมอง (peephole connections):

กลไกเพิ่มเติม สำหรับแบบจำลองความจำระยะสั้นที่ยาว เพื่อช่วยให้การควบคุมเปลี่ยนค่าสถานะและค่าผลลัพธ์ของหน่วยคำนวณ ทำได้แม่นยำมากขึ้น โดยนำค่าสถานะเข้าไปเป็นส่วนหนึ่งในการพิจารณาการเปิดปิดของประตูด้วย.

สถาปัตยกรรมตัวเข้ารหัสตัวถอดรหัส (encoder-decoder architecture):

โครงสร้างการต่อเชื่อมที่ใช้โครงข่ายประสาทเวียนกลับสองตัวต่อกัน โดยให้ตัวหนึ่งประมวลผลชุดลำดับอินพุต และอีกตัวประมวลผลชุดลำดับเอาต์พุต สำหรับภารกิจจำลองแบบชุดลำดับเป็นชุดลำดับ.

การประมวลผลภาษาธรรมชาติ (Natural Language Processing คำย่อ NLP):

ศาสตร์ที่ใช้วิธีการต่าง ๆ เพื่อให้คอมพิวเตอร์สามารถนำข้อความในภาษาธรรมชาติไปประมวลผล และให้ผลลัพธ์ตามจุดประสงค์ของภาระกิจที่ต้องการ.

โทเค็น (token):

หน่วยพื้นฐานของภาษาที่มีความหมาย เช่น โทเค็น อาจหมายถึง คำ.

ไวยากรณ์ (syntax):

กฎเกณฑ์ที่เกี่ยวกับโทเค็น และโครงสร้าง.

การแจกส่วน (parsing):

การวิเคราะห์โครงสร้างไวยากรณ์ของข้อความหรือประโยค.

การระบุหมวดคำ (Part-Of-Speech Tagging):

ภารกิจที่ระบุว่า คำต่าง ๆ ในข้อความ แต่ละคำอยู่ในหมวดคำใด จากหมวดคำ เช่น นาม สรรพนาม กริยา วิเศษณ์ คุณศัพท์ สันธาน บุพบท อุทาน.

ภารกิจจำลองแบบชุดลำดับเป็นชุดลำดับ (sequence-to-sequence modeling task):

ภารกิจที่ทั้งอินพุตและเอาต์พุตเป็นชุดลำดับ แต่จำนวนลำดับของชุดอินพุต อาจไม่เท่ากับจำนวนลำดับในชุดเอาต์พุต

กลไกความใส่ใจ (attention mechanism):

กลไกสำหรับภารกิจจำลองแบบชุดลำดับเป็นชุดลำดับ เพื่อช่วยบรรเทาปัญหา เมื่อทำงานกับชุดลำดับที่ยาว.