8 แบบจำลองสำหรับข้อมูลเชิงลำดับ
“Failure comes only when we forget our ideals and objectives and principles.”
—Jawaharlal Nehru
“ความล้มเหลวมาก็แต่เฉพาะตอนที่เราลืมอุดมการณ์ เป้าหมาย และหลักการของเรา.”
—ชวาหะร์ลาล เนห์รู
รูปแบบของข้อมูลในเนื้อหาที่ผ่าน ๆ มา เป็นลักษณะที่เป็นอิสระในตัวเอง นั่นคือ แต่ละจุดข้อมูลมีความหมายสมบูรณ์แบบในตัวเอง หรือหากเจาะจงลงไป อาจกล่าวว่า ที่ผ่านมา แต่ละจุดข้อมูลเป็นอิสระต่อกันและมีการแจกแจงเหมือนกัน ที่เรียกว่า ไอ.ไอ.ดี. (independent and identically distributed คำย่อ i.i.d.). อย่างไรก็ตาม มีข้อมูลหลายประเภทที่จุดข้อมูลต่าง ๆ มีความสัมพันธ์ระหว่างกัน. เนื้อหาในบทนี้อภิปรายแนวทางและแบบจำลอง ที่ออกแบบมาสำหรับการทำงานอย่างมีประสิทธิภาพกับข้อมูลเชิงลำดับ.
8.1 ข้อมูลเชิงลำดับ
ข้อมูลประเภทที่จุดข้อมูลมีความสัมพันธ์เชิงลำดับระหว่างกัน จะเรียกว่า ข้อมูลเชิงลำดับ (sequential data). นั่นคือ แม้ว่าจุดข้อมูลจะมีค่าเหมือนกัน แต่หากลำดับที่ปรากฏต่างกัน ก็อาจทำให้ความหมายต่างกัน หรือแม้จุดข้อมูลหนึ่งจะมีค่าเท่าเดิมและปรากฏที่ตำแหน่งเดิม แต่หากจุดข้อมูลอื่น ๆ ในลำดับเปลี่ยนค่า ก็อาจจะทำให้ความหมายนั้นเปลี่ยนไปได้.
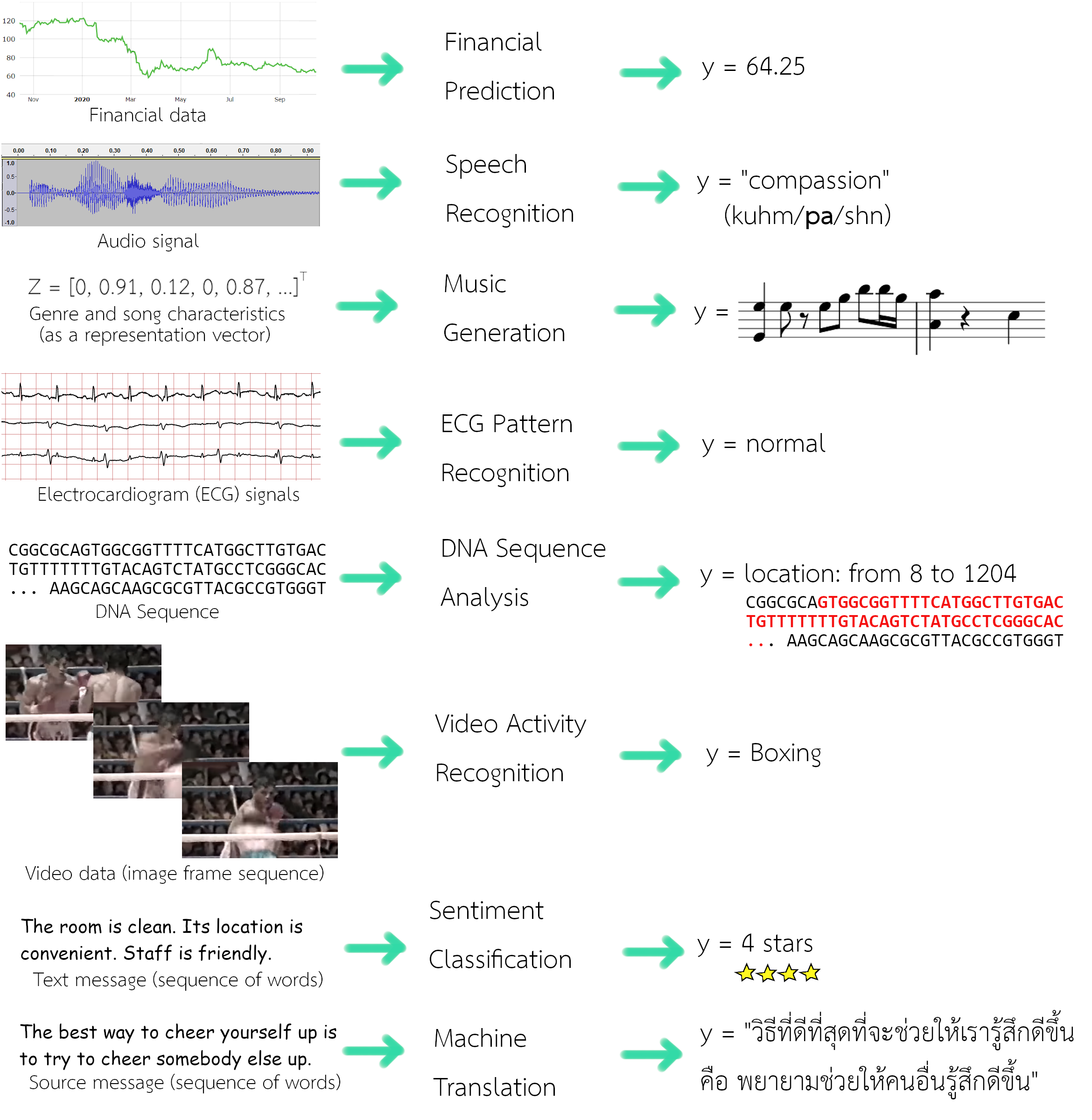
ข้อมูลหลากหลายชนิด เป็นข้อมูลเชิงลำดับ และงานการรู้จำรูปแบบกับข้อมูลเชิงลำดับ ก็มีหลากหลายประเภท เช่น การทำนายข้อมูลทางการเงิน (financial data prediction) ซึ่งอาจรับอินพุตเป็นลำดับของราคาปิดของหุ้นในวันก่อน ๆ และทำนายราคาปิดของวันถัดไป, การรู้จำเสียงพูด (speech recognition) ที่รับอินพุตเป็นสัญญาณเสียง (ลำดับค่าแอมพลิจูดต่อเวลา) และให้เอาต์พุตเป็นลำดับของคำ, ระบบแต่งเพลงอัตโนมัติ (music generation) ที่อาจรับอินพุตเป็นประเภทของเพลง และให้เอาต์พุตเป็นลำดับของโน๊ตดนตรี, การรู้จำรูปแบบสัญญาณคลื่นไฟฟ้าหัวใจ (ECG pattern recognition) ที่รับอินพุตเป็นสัญญาณคลื่นไฟฟ้าหัวใจ (ลำดับแอมพลิจูดหลาย ๆ ช่องสัญญาณต่อเวลา) และอาจจะให้เอาต์พุตเป็นค่าระบุว่า ปกติหรือผิดปกติ หรืออาจระบุตำแหน่งและชนิดที่ผิดปกติออกมาด้วย, ระบบวิเคราะห์ลำดับดีเอ็นเอ (DNA sequence analysis) ที่รับอินพุตเป็นลำดับของชนิดฐานนิวคลีโอไทด์ และอาจจะให้เอาต์พุตเป็นตำแหน่งต่าง ๆ ในลำดับที่สัมพันธ์กับโปรตีนที่สนใจ, การรู้จำกิจกรรมจากวีดีโอ (video activity recognition) ที่รับอินพุตเป็นข้อมูลวีดีโอ (ลำดับของภาพต่าง ๆ ตามเวลา) และให้เอาต์พุตเป็นฉลากของกิจกรรม, การจำแนกอารมณ์ (sentiment classification) ที่อาจรับอินพุตเป็นข้อความ (ลำดับของคำต่าง ๆ) และให้เอาต์พุตเป็นคะแนนประเมินความพอใจ, การแปลภาษาอัตโนมัติ (machine translation) ที่รับอินพุตเป็นข้อความในภาษาหนึ่ง (ลำดับของคำในภาษาต้นทาง) และให้เอาต์พุตเป็นข้อความในอีกภาษาหนึ่ง (ลำดับของคำในภาษาเป้าหมาย). สำหรับข้อมูลเชิงลำดับบางชนิด ตัวลำดับอาจเป็นตัวแทนของเวลา เช่น สัญญาณเสียง หรืออาจเป็นเพียงลำดับที่ไม่ได้เกี่ยวกับเวลาก็ได้ เช่น ลำดับของคำต่าง ๆ ในข้อความ. อย่างไรก็ตาม เพื่อความสะดวก เนื้อหาในบทนี้อาจใช้คำว่า เวลา ในการอ้างถึงลำดับ. รูป 1.1 แสดงตัวอย่างข้อมูลเชิงลำดับ และตัวอย่างภาระกิจการรู้จำรูปแบบที่เกี่ยวข้อง.
หากจำแนกภาระกิจออกตามลักษณะอินพุตและเอาต์พุต การรู้จำรูปแบบเชิงลำดับ อาจจำแนกได้ดังนี้. (1) ประเภทแรกคือ ภาระกิจที่อินพุตเป็นข้อมูลลำดับ \(\{\boldsymbol{x}_n\}_{n=1,\ldots, N}\) เมื่อ \(N\) คือจำนวนจุดข้อมูลทั้งหมดในลำดับ แต่เอาต์พุตไม่ได้เป็นข้อมูลลำดับ \(y \in \mathbb{R}^K\) เมื่อ \(K\) คือจำนวนมิติของเอาต์พุต. ในรูป 1.1 ตัวอย่างในกลุ่มนี้คือ การทำนายข้อมูลทางการเงิน, การรู้จำรูปแบบสัญญาณคลื่นไฟฟ้าหัวใจ, การรู้จำกิจกรรมจากวีดีโอ และการจำแนกอารมณ์. ระบบวิเคราะห์ลำดับดีเอ็นเอ ก็อาจจัดอยู่ในกลุ่มนี้ หากให้เอาต์พุตออกมาเป็นค่าดัชนีของจุดเริ่มต้นและจุดจบของส่วนลำดับที่สนใจ. (2) ประเภทสองคือ ภาระกิจที่อินพุตเป็นข้อมูลลำดับ \(\{\boldsymbol{x}_n\}_{n=1,\ldots, N}\) และเอาต์พุตก็เป็นข้อมูลลำดับ \(\{\boldsymbol{y}_n\}_{n=1,\ldots, N}\) โดยทั้งสองลำดับมีจำนวนจุดข้อมูลในลำดับเท่ากัน. รูป 1.1 ไม่ได้แสดงตัวอย่างของภาระกิจในกลุ่มนี้. ตัวอย่างภาระกิจในกลุ่มนี้ ได้แก่ การระบุหมวดคำ (Part-Of-Speech Tagging) ที่วิเคราะห์ข้อความแล้วระบุหมวดคำของคำทุกคำในข้อความ ว่าอยู่ในหมวดคำใดในกลุ่ม (ซึ่งมักประกอบด้วย คำนาม, คำกริยา, คำคุณศัพท์, คำกริยาวิเศษณ์, คำบุพบท, คำสันธาน, คำสรรพนาม, คำอุทาน และคำนำหน้านาม สำหรับภาระกิจการระบุหมวดคำในภาษาอังกฤษ) และการรู้จำชื่อเฉพาะ (Named-Entity Recognition) ที่ต้องการระบุว่าคำไหนบ้างในข้อความที่เป็นชื่อเฉพาะ และเป็นชื่อเฉพาะของสิ่งประเภทใด (ซึ่งมักกำหนดประเภทที่สนใจไว้ เช่น ชื่อคน, ชื่อองค์กร หน่วยงาน หรือบริษัท, ชื่อตราสินค้า, ชื่อสถานที่, เวลา, ปริมาณหรือจำนวน) เป็นต้น. (3) ประเภทสามคือ ภาระกิจที่อินพุตเป็นข้อมูลลำดับ \(\{\boldsymbol{x}_n\}_{n=1,\ldots, N}\) และเอาต์พุตก็เป็นข้อมูลลำดับ \(\{\boldsymbol{y}_n\}_{n=1,\ldots, M}\) เมื่อ \(M\) เป็นจำนวนจุดข้อมูลในลำดับของเอาต์พุต แต่ลำดับทั้งสองอาจมีจำนวนจุดข้อมูลในลำดับไม่เท่ากัน. ตัวอย่างที่แสดงในรูป 1.1 คือ การแปลภาษาอัตโนมัติ ที่ข้อความของภาษาต้นทาง อาจมีจำนวนคำต่างจากข้อความของภาษาปลายทาง. (4) ประเภทสี่คือ ภาระกิจที่อินพุตไม่ใช่ข้อมูลลำดับ แต่เอาต์พุตเป็นข้อมูลลำดับ. ตัวอย่างที่แสดงในรูป 1.1 คือ ระบบแต่งเพลงอัตโนมัติ ที่อินพุตอาจจะเป็นเวกเตอร์ หรืออาจจะเป็นค่าสเกล่าร์ แต่ให้เอาต์พุตออกมาเป็นลำดับของดนตรี. สุดท้าย หากภาระกิจที่ทั้งอินพุตและเอาต์พุตไม่ใช่ข้อมูลลำดับ ภาระกิจนี้ไม่จัดอยู่ในการรู้จำรูปแบบเชิงลำดับ และโดยทั่วไป ภาระกิจประเภทนี้จะสามารถดำเนินการได้ โดยวิธีการต่าง ๆ ที่ได้อภิปรายไปในบทก่อน ๆ.
ข้อมูลเชิงลำดับ อาจแบ่งออกได้เป็นสองประเภท คือ ข้อมูลเชิงลำดับแบบคงที่ กับ ข้อมูลเชิงลำดับแบบไม่คงที่. ข้อมูลเชิงลำดับแบบคงที่ (stationary sequential data) ที่แม้ค่าต่าง ๆ ของจุดข้อมูลอาจผันแปรไปตามเวลา แต่การแจกแจงเบื้องหลังลำดับข้อมูลนั้นคงที่ ไม่ได้มีการเปลี่ยนแปลงตามเวลา. ส่วนกรณีของข้อมูลเชิงลำดับแบบไม่คงที่ (nonstationary sequential data) การแจกแจงเบื้องหลังลำดับข้อมูลนั้นมีการเปลี่ยนแปลงตามเวลาด้วย. หากอธิบายง่าย ๆ อาจเปรียบเทียบจาก ตัวอย่างของข้อมูลปริมาณน้ำฝนในแต่ละวัน ตลอดหลาย ๆ ปี โดยที่ระยะเวลาเหล่านั้นฟ้าฝนตกต้องตามฤดูกาล เป็นตัวอย่างของข้อมูลเชิงลำดับแบบคงที่. ส่วนตัวอย่างของข้อมูลปริมาณน้ำฝนในแต่ละวัน ในหลาย ๆ ปีให้หลังมานี้ ซึ่งสังเกตได้ชัดว่าฟ้าฝนตกผิดเพี้ยนจากฤดูกาลที่คุ้นเคย. การเปลี่ยนแปลงเกิดที่ตัวของฤดูกาลเองอย่างมาก ที่อาจจะเกิดจากหลาย ๆ สาเหตุรวมถึงภาวะโลกร้อนสภาพภูมิอากาศเปลี่ยนแปลง. กรณีหลังนี้ เป็นตัวอย่างของข้อมูลเชิงลำดับแบบไม่คงที่ ซึ่งการเปลี่ยนแปลงตามเวลาของข้อมูล เกิดจากกระบวนการเบื้องหลังที่มีการเปลี่ยนแปลงตัวกระบวนการไปตามเวลาด้วย. เนื้อหาในบทนี้ใช้สมมติฐานของกรณีข้อมูลเชิงลำดับแบบคงที่เป็นหลัก ยกเว้นแต่จะระบุเป็นอื่น.
การสร้างแบบจำลองสำหรับข้อมูลเชิงลำดับ สามารถทำได้หลายแนวทาง. หัวข้อ 1.2 และ 1.3 อภิปรายแนวทางการใช้ความน่าจะเป็นด้วยแบบจำลองมาร์คอฟ และแบบจำลองมาร์คอฟซ่อนเร้น. แนวทางของโครงข่ายประสาทเวียนกลับ จะถูกอภิปรายในหัวข้อ [sec: RNN].
8.2 แบบจำลองมาร์คอฟ
การสร้างแบบจำลองสำหรับข้อมูลเชิงลำดับ โดยรองรับความสัมพันธ์เชิงลำดับระหว่างลำดับต่าง ๆ อย่างสมบูรณ์ อาจทำให้การคำนวณทำได้ยาก. ตัวอย่างเช่น สำหรับภารกิจการทำนายค่าในอนาคต นั่นคือ การทำนายจุดข้อมูลลำดับต่อไป \(\boldsymbol{x}_{T+1}\) ของข้อมูลชุดลำดับ \(\{\boldsymbol{x}_t\}_{t=1,\ldots, T}\). การใช้แบบจำลองความน่าจะเป็น 1 ด้วย \(p(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_T)\) อาจอาศัยทฤษฎีของเบส์ (หัวข้อ [sec: cond prob]) เพื่อประมาณค่าในอนาคตด้วย \(p(\boldsymbol{x}_{T+1}|\boldsymbol{x}_1, \boldsymbol{x}_2,\) \(\ldots, \boldsymbol{x}_T) = p(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_T, \boldsymbol{x}_{T+1})/p(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_T)\). ค่า \(p(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_T)\) เอง ก็ประมาณได้ยากในทางปฏิบัติ และถึงแม้จะรู้ แต่ค่าของ \(p(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots\) \(,\boldsymbol{x}_T, \boldsymbol{x}_{T+1})\) ยิ่งยากกว่าที่จะประมาณ หากยังใช้แบบจำลองที่รองรับความสัมพันธ์เชิงลำดับระหว่างลำดับต่าง ๆ อย่างสมบูรณ์.
แนวทางการแก้ปัญหาเชิงคำนวณหลาย ๆ ครั้ง ที่การคำนวณค่าอย่างแม่นตรง (exact calculation) ไม่สามารถทำได้หรือทำได้ยาก การประมาณหรือการเพิ่มเงื่อนไขที่สมเหตุสมผล มักถูกนำมาใช้. วิธีหนึ่งคือ เลือกการประมาณที่สุดขอบ เช่น การประมาณโดยไม่สนใจความสัมพันธ์เชิงลำดับเลย (ใช้สมมติฐาน ไอ.ไอ.ดี.) ซึ่งวิธีนี้ทำให้เราสามารถเลือกแบบจำลองต่าง ๆ ที่ไม่มีความสามารถเชิงลำดับ เช่น โครงข่ายประสาทเทียม (บทที่ [chapter: ANN]) มาใช้ก็ได้. แต่การประมาณที่สุดขอบเช่นนี้ เท่ากับเราทิ้งสารสนเทศความสัมพันธ์เชิงลำดับไปทั้งหมดเลย. เราไม่สามารถใช้ประโยชน์จากสารสนเทศเชิงลำดับได้เลย.
ยืดหยุ่นขึ้นมาบ้าง แบบจำลองมาร์คอฟ (Markov models หรืออาจเรียก Markov chain) ประมาณความสัมพันธ์เชิงลำดับโดยจำกัดเฉพาะลำดับที่ผ่านมาไม่กี่ลำดับ. จุดสำคัญ คือ (1) แบบจำลองมาร์คอฟ จำกัดความสัมพันธ์เชิงลำดับ โดยจำกัดให้ค่าของจุดข้อมูลมีความสัมพันธ์เฉพาะกับค่าของจุดข้อมูลลำดับก่อนหน้า. จุดข้อมูลลำดับหลังไม่จำเป็น. นั่นคือ \(p(\boldsymbol{x}_t| \boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_{t-1}, \boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T)\) \(=p(\boldsymbol{x}_t| \boldsymbol{x}_1, \boldsymbol{x}_2, \ldots,\) \(\boldsymbol{x}_{t-1})\). (2) แบบจำลองมาร์คอฟ จำกัดความสัมพันธ์เชิงลำดับกลับไปเพียงจำนวนลำดับที่กำหนดเท่านั้น. ไม่ได้ย้อนกลับไปจนถึงจุดข้อมูลที่ลำดับแรกสุดทุกครั้ง. นั่นคือ แบบจำลองมาร์คอฟประมาณ \(p(\boldsymbol{x}_{T+1}|\boldsymbol{x}_1, \boldsymbol{x}_2,\) \(\ldots, \boldsymbol{x}_T) = p(\boldsymbol{x}_{T+1}|\boldsymbol{x}_{T+1-\tau}, \ldots, \boldsymbol{x}_T)\) เมื่อ \(\tau\) เป็นจำนวนจุดข้อมูลในลำดับก่อนหน้าที่แบบจำลองมาร์คอฟถือว่ามีความสัมพันธ์. อภิมานพารามิเตอร์ \(\tau\) ที่นิยมเลือกใช้คือ \(\tau = 1\) ซึ่งแบบจำลองมาร์คอฟที่ใช้ \(\tau = 1\) จะเรียกว่า แบบจำลองมาร์คอฟอันดับหนึ่ง (first-order Markov model). นั่นคือ \[\begin{eqnarray} p(\boldsymbol{x}_{T+1}|\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_T) &=& p(\boldsymbol{x}_{T+1}|\boldsymbol{x}_T) \label{eq: seq first-order markov criteria} \end{eqnarray}\] เมื่อลำดับ \(\{\boldsymbol{x}_t\}\) มีความสัมพันธ์เชิงลำดับตามเงื่อนไขของมาร์คอฟ. รูป 1.2 แสดงเงื่อนไขมาร์คอฟ เปรียบเทียบกับสมมติฐานอื่น ๆ. เนื่องจากแบบจำลองมาร์คอฟอันดับหนึ่งเป็นที่นิยมเป็นอย่างมาก ทำให้หลาย ๆ ครั้งการอ้างถึงแบบจำลองมาร์คอฟ หมายถึงแบบจำลองมาร์คอฟอันดับหนึ่ง. เพื่อความกระชับ เนื้อหาต่อไปนี้ก็จะอ้างถึงแบบจำลองมาร์คอฟอันดับหนึ่งว่า แบบจำลองมาร์คอฟ ยกเว้นแต่จะระบุเป็นอื่น.

ด้วยแบบจำลองมาร์คอฟ การแจกแจงร่วมของลำดับข้อมูลสามารถวิเคราะห์ได้จาก \[\begin{eqnarray} p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_T) &=& p(\boldsymbol{x}_1) \cdot \prod_{t=2}^T p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1}) \label{eq: seq markov chain} . \end{eqnarray}\]
การแจกแจงแบบมีเงื่อนไข \(p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})\) สามารถถูกกำหนดให้มีค่าเท่ากันทุก ๆ ดัชนีลำดับ \(t\) ตามสมมติฐานข้อมูลเชิงลำดับแบบคงที่. การกำหนดเช่นนี้ ช่วยให้เราสามารถใช้ค่าพารามิเตอร์ร่วมกันได้ 2 ซึ่งมีผลช่วยลดความซับซ้อนของการคำนวณ และช่วยลดปริมาณข้อมูลที่ต้องการสำหรับการฝึกแบบจำลองด้วย. แบบจำลองมาร์คอฟ ช่วยให้การประมาณการแจกแจงร่วมของข้อมูลลำดับคำนวณได้สะดวกขึ้น.
แต่อย่างไรก็ตาม เงื่อนไขการขึ้นอยู่กับค่าจุดข้อมูลก่อนหนึ่งเพียงหนึ่งลำดับ ก็เป็นปัจจัยจำกัดความสามารถของแบบจำลองมาร์คอฟลงด้วย. เราอาจจะเพิ่มอันดับ (เพิ่มค่า \(\tau\)) ของแบบจำลองมาร์คอฟขึ้น ซึ่งก็จะอาจจะช่วยบรรเทาข้อจำกัดลงได้บ้าง ในเรื่องความสามารถที่จะเชื่อมโยงความสัมพันธ์เชิงลำดับระยะที่ยาวขึ้น. แต่แนวทางนี้ กลับส่งผลลบต่อประสิทธิภาพการคำนวณเป็นอย่างมาก (ศึกษารายละเอียดเพิ่มเติมจาก ).
เพื่อแบบจำลองจะไม่ถูกจำกัดจำนวนลำดับย้อนหลังที่สัมพันธ์กันจากเงื่อนไขของมาร์คอฟ และก็ยังสามารถคำนวณได้อย่างมีประสิทธิภาพ เราสามารถดัดแปลงแบบจำลองได้โดยกำหนดให้ จุดข้อมูล \(\boldsymbol{x}_t\) สัมพันธ์กับสถานะ \(\boldsymbol{z}_t\) และสถานะ \(\boldsymbol{z}_t\) เป็นไปตามเงื่อนไขของมาร์คอฟ. เงื่อนไขเช่นนี้ ช่วยให้แบบจำลองมีความยืดหยุ่น สามารถรองรับความสัมพันธ์ของจุดข้อมูลย้อนหลังกี่ลำดับก็ได้ โดยผ่านกลไกของตัวแปรสถานะ และยังคงรักษาการคำนวณที่มีประสิทธิภาพไว้ได้.
ค่าของสถานะ \(\boldsymbol{z}_t\) อาจมีความหมายชัดเจนหรือไม่ก็ได้ และอาจสามารถสังเกตได้โดยตรงหรือไม่ก็ได้. ดังนั้น สถานะ \(\boldsymbol{z}_t\) จึงถูกเรียกว่า สถานะซ่อนเร้น (latent state) หรือตัวแปรซ่อนเร้น (latent variable) และเงื่อนไขนี้ เรียกว่า เงื่อนไขมาร์คอฟซ่อนเร้น (hidden Markov criteria). บางครั้ง เพื่อลดความสับสน ตัวแปรจุดข้อมูล \(\boldsymbol{x}_t\) อาจถูกเรียกว่า ตัวแปรที่ถูกสังเกต (observed variable). รูป 1.2 แสดงเงื่อนไขมาร์คอฟซ่อนเร้น (ภาพสุดท้าย) เปรียบเทียบกับสมมติฐานอื่น ๆ.
ค่าของสถานะซ่อนเร้น \(\boldsymbol{z}_t\) อาจจะเป็นค่าชนิดเดียวกับค่าของจุดข้อมูล \(\boldsymbol{x}_t\) ก็ได้ หรืออาจจะต่างกันก็ได้ เช่น ค่าของสถานะอาจเป็นค่าวิยุตที่มีจำนวนจำกัด แต่ค่าของจุดข้อมูล \(\boldsymbol{x}_t\) อาจจะเป็นค่าวิยุตที่มีจำนวนจำกัด หรือค่าวิยุตที่มีจำนวนไม่จำกัด หรือค่าต่อเนื่องก็ได้. จำนวนมิติของสถานะซ่อนเร้น อาจจะเท่ากับ หรืออาจจะต่างจากจำนวนมิติของตัวแปรจุดข้อมูลก็ได้. เงื่อนไขมาร์คอฟซ่อนเร้น เพียงระบุว่า ความเป็นอิสระต่อกันแบบมีเงื่อนไข นั่นคือ \(\boldsymbol{z}_t \perp \!\!\! \perp \boldsymbol{z}_{t-2} | \boldsymbol{z}_{t-1}\) และ \(\boldsymbol{x}_t \perp \!\!\! \perp \boldsymbol{x}_{t-1} | \boldsymbol{z}_t\).
ด้วยเงื่อนไขมาร์คอฟซ่อนเร้น การแจกแจงร่วมของลำดับชุดข้อมูลและชุดสถานะ สามารถเขียนได้ \[\begin{eqnarray} p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_T, \boldsymbol{z}_1, \ldots, \boldsymbol{z}_T) &=& p(\boldsymbol{z}_1) \cdot \left( \prod_{t=2}^T p(\boldsymbol{z}_t|\boldsymbol{z}_{t-1}) \right) \cdot \prod_{t=1}^T p(\boldsymbol{x}_t|\boldsymbol{z}_t) \label{eq: seq state space model} . \end{eqnarray}\] แบบจำลองตามเงื่อนไขมาร์คอฟซ่อนเร้น เรียกว่า แบบจำลองปริภูมิสถานะ (state space model). แบบจำลองปริภูมิสถานะ มีแบบจำลองที่เฉพาะเจาะจงลงไปอีก ที่สำคัญได้แก่ แบบจำลองมาร์คอฟซ่อนเร้น ที่เจาะจงสำหรับกรณีสถานะซ่อนเร้นเป็นตัวแปรวิยุต และแบบจำลองพลวัตเชิงเส้น (linear dynamic model หรือ linear dynamic system) ที่เจาะจงสำหรับกรณีที่ทั้งสถานะซ่อนเร้นและตัวแปรที่ถูกสังเกตเป็นตัวแปรต่อเนื่องที่มีการแจกแจงเกาส์เซียน.
8.3 แบบจำลองมาร์คอฟซ่อนเร้น
แบบจำลองมาร์คอฟซ่อนเร้น 3 (hidden Markov model) เป็นแบบจำลองสำหรับข้อมูลเชิงลำดับ ที่ใช้เงื่อนไขมาร์คอฟซ่อนเร้น สำหรับกรณีที่สถานะซ่อนเร้นเป็นตัวแปรวิยุต ที่ค่าวิยุตมีจำนวนจำกัด. เมื่อพิจารณาสมการ \(\eqref{eq: seq state space model}\) ด้วยสมมติฐานสถานะซ่อนเร้นวิยุต เราจะเห็นว่า สำหรับ ระบบที่มีค่าของสถานะซ่อนเร้นได้ \(K\) สถานะแล้ว ความน่าจะเป็น \(p(\boldsymbol{z}_1)\) ที่อาจเรียกว่า ค่าความน่าจะเป็นเริ่มต้น (initial probabilities) สามารถแทนด้วยตารางความน่าจะเป็น โดยแต่ละรายการของตารางระบุค่าความน่าจะเป็น \(p(\boldsymbol{z}_1 =k) = \pi_k\) สำหรับ \(k = 1, \ldots, K\) เมื่อ \(\pi_k\) เป็นความน่าจะเป็นที่ระบบจะเริ่มต้นด้วยสถานะ \(k\). ค่าของ \(\pi_k\) ต่าง ๆ เป็นพารามิเตอร์ของแบบจำลอง (กระบวนการหาค่าพารามิเตอร์เหล่านี้ จะอภิปรายในหัวข้อ 1.3.1.)
ความน่าจะเป็น \(p(\boldsymbol{z}_t|\boldsymbol{z}_{t-1})\) ที่เรียกว่า ความน่าจะเป็นของการเปลี่ยนสถานะ (transition probabilities) สามารถแทนด้วยเมทริกซ์ \(\boldsymbol{A}\) ที่ส่วนประกอบ \(A_{ij}\) แทนความน่าจะเป็นของการเปลี่ยนสถานะจากสถานะ \(i\) ไปเป็นสถานะ \(j\). เมทริกซ์ \(\boldsymbol{A}\) อาจถูกเรียกว่า เมทริกซ์การเปลี่ยนสถานะ (transition matrix).
เพื่อความสะดวก สถานะซ่อนเร้นได้ \(K\) สถานะ สามารถแสดงด้วยรหัสหนึ่งร้อน (one-hot coding ดูหัวข้อ [sec: ann classification]) ซึ่งคือ สถานะซ่อนเร้น \(\boldsymbol{z}_t = [z_{t,1}, \ldots, z_{t,K}]^T \in \{0,1\}^K\) และ \(\sum_{k=1}^K z_{t,k} = 1\). ดังนั้น \(\pi_k \equiv p(z_{1,k} = 1)\) และ \(A_{ij} \equiv p(z_{t,j}=1|z_{t-1,i}=1)\). หมายเหตุ ด้วยสมมติฐานข้อมูลเชิงลำดับแบบคงที่ ความน่าจะเป็นของการเปลี่ยนสถานะ \(p(\boldsymbol{z}_t|\boldsymbol{z}_{t-1})\) จะถูกแทนด้วยเมทริกซ์การเปลี่ยนสถานะ \(\boldsymbol{A}\) เหมือนกันสำหรับทุก ๆ ค่าของลำดับ \(t\). นอกจากนั้น ด้วยคุณสมบัติความน่าจะเป็น ทำให้รู้ว่า \(0 \leq \pi_k, A_{ij} \leq 1\) สำหรับทุก ๆ ค่าของ \(i, j, k\) กับ \(\sum_{k=1}^K \pi_k = 1\) และ \(\sum_{j=1}^K A_{ij} = 1\).
เช่นเดียวกับพารามิเตอร์ \(\boldsymbol{\pi} = [\pi_1, \ldots, \pi_K]^T\) เมทริกซ์ \(\boldsymbol{A}\) ก็เป็นพารามิเตอร์ของแบบจำลอง. เราสามารถเขียนฟังก์ชันการแจกแจงเริ่มต้น และฟังก์ชันการแจกแจงการเปลี่ยนสถานะ โดยเน้นพารามิเตอร์เหล่านี้ได้ 4 \[\begin{eqnarray} p(\boldsymbol{z}_1|\boldsymbol{\pi}) &=& \prod_{k=1}^K \pi_k^{z_{1k}} \label{eq: seq HMM p(z|pi)} . \\ p(\boldsymbol{z}_t|\boldsymbol{z}_{t-1}, \boldsymbol{A}) &=& \prod _{j=1}^K \prod_{i=1}^K A_{ij}^{z_{t-1,i} \cdot z_{t,j}} \label{eq: seq HMM p(z|z,A)} . \end{eqnarray}\] ตัวอย่างเช่น สำหรับระบบที่มีสามสถานะซ่อนเร้น การคำนวณฟังก์ชันการแจกแจงเริ่มต้น สำหรับสถานะที่หนึ่ง (\(\boldsymbol{z}_1 = [1,0,0]^T\)) ทำโดย \(p(\boldsymbol{z}_1 = [1,0,0]^T|\boldsymbol{\pi}) = \pi_1^1 \cdot \pi_2^0 \cdot \pi_3^0 = \pi_1\).
สุดท้ายฟังก์ชันการแจกแจงแบบมีเงื่อนไข สำหรับตัวแปรที่ถูกสังเกต \(p(\boldsymbol{x}_t|\boldsymbol{z}_t)\) มักถูกเรียกว่า ความน่าจะเป็นของการปล่อย (emission probabilities). เช่นเดียวกัน ด้วยสมมติฐานข้อมูลเชิงลำดับแบบคงที่ ความน่าจะเป็นของการปล่อย ไม่ขึ้นกับดัชนีลำดับ \(t\). เราอาจเขียนความน่าจะเป็นของการปล่อยด้วย \(p(\boldsymbol{x}|\boldsymbol{z})\) โดยละดัชนีลำดับออกได้.
ความน่าจะเป็นของการปล่อย อาจถูกนิยามด้วยการแจกแจงที่เหมาะสมกับลักษณะของตัวแปรที่ถูกสังเกต เช่น หากตัวแปรที่ถูกสังเกตเป็นค่าวิยุต เราอาจประมาณความน่าจะเป็นของการปล่อย ด้วยเมทริกซ์แจกแจง \(\boldsymbol{\Phi}\) ที่ส่วนประกอบ \(\phi_{kd}\) ระบุค่าความน่าจะเป็นที่ตัวแปรที่ถูกสังเกตจะเป็นชนิดที่ \(d^{th}\) เมื่อสถานะซ่อนเร้นเป็นสถานะที่ \(k^{th}\). นั่นคือ \(p(\boldsymbol{x}|\boldsymbol{z}, \boldsymbol{\Phi}) = \prod_d \prod_k \phi_{kd}^{z_k \cdot x_d}\) เมื่อ \(\phi_{kd} \equiv p(x_d = 1|z_k =1)\) และทั้ง \(\boldsymbol{x}\) และ \(\boldsymbol{z}\) แสดงด้วยรหัสหนึ่งร้อน. หากตัวแปรที่ถูกสังเกตเป็นค่าต่อเนื่อง เราอาจเลือกการแจกแจงเกาส์เซียน สำหรับประมาณความน่าจะเป็นของการปล่อย. นั่นคือ \(p(\boldsymbol{x}|\boldsymbol{z}, \{\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i\}_{i=1,\ldots,K}) = \prod_{k=1}^K \left(\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)\right)^{z_k}\) เมื่อ \(\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) = \frac{1}{ \sqrt{ (2\pi)^D | \boldsymbol{\Sigma}_k |} } \exp \left( -\frac{1}{2} (\boldsymbol{x} -\boldsymbol{\mu}_k)^T \boldsymbol{\Sigma}_k^{-1} (\boldsymbol{x} -\boldsymbol{\mu}_k) \right)\) โดย \(D\) เป็นจำนวนมิติของเวกเตอร์ \(\boldsymbol{x}\) และ \(\{\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i\}_{i=1,\ldots,K}\) เป็นพารามิเตอร์ของแบบจำลอง. หมายเหตุ ค่า \(\pi\) ในที่นี้หมายถึง ค่าคงที่ไพ (\(\pi \approx 3.1416\)) ซึ่งต่างจาก \(\pi_k\) (เช่นในสมการ \(\eqref{eq: seq HMM p(z|pi)}\)) ที่เป็นพารามิเตอร์ของแบบจำลอง. สังเกตว่า ถึงแม้แบบจำลองมาร์คอฟซ่อนเร้น จะกำหนดให้สถานะซ่อนเร้น \(\boldsymbol{z}\) เป็นตัวแปรค่าวิยุต แต่ตัวแปรที่ถูกสังเกต \(\boldsymbol{x}\) อาจจะเป็นค่าวิยุต หรือเป็นค่าต่อเนื่องก็ได้.
เพื่อความสะดวก ต่อจากนี้ พารามิเตอร์ของฟังก์ชันประมาณความน่าจะเป็นของการปล่อย จะถูกอ้างถึงโดยรวมด้วยสัญกรณ์ \(\boldsymbol{\phi}\) ไม่ว่าจะเลือกใช้การแจกแจงแบบใด และ \(\boldsymbol{\phi}_k\) จะหมายถึงชุดพารามิเตอร์ของการแจกแจง ของสถานะซ่อนเร้น \(k^{th}\) เช่น กรณีเมทริกซ์แจกแจง \(\boldsymbol{\phi}_k \equiv \prod_d \phi_{kd}^{x_d}\) หรือกรณีเกาส์เซีียน \(\boldsymbol{\phi}_k \equiv \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)\). นั่นคือ ฟังก์ชันประมาณความน่าจะเป็นของการปล่อย หรือเรียกย่อ ๆ ว่า ฟังก์ชันการปล่อย (emission function) จะใช้สัญกรณ์ \(p(\boldsymbol{x}|\boldsymbol{z}, \boldsymbol{\phi})\) โดย \(\boldsymbol{\phi}\) หมายถึงพารามิเตอร์ของแบบจำลองที่ใช้ (อาจจะหมายถึง เมทริกซ์ \(\boldsymbol{\Phi}\) หรือเซต \(\{\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i\}_{i=1,\ldots,K}\) หรือชุดพารามิเตอร์อื่น ๆ ตามการแจกแจงที่เลือก). ฟังก์ชันการปล่อย อาจเขียนได้ โดยทั่วไปเป็น \[\begin{eqnarray} p(\boldsymbol{x}_t|\boldsymbol{z}_t, \boldsymbol{\phi}) &=& \prod_{k=1}^K \left( p(\boldsymbol{x}_t| \boldsymbol{\phi}_k ) \right)^{z_{t,k}} \label{eq: seq HMM emission} . \end{eqnarray}\]
การแจกแจงร่วมของข้อมูลหนึ่งลำดับชุด สามารถเขียนได้เป็น \[\begin{eqnarray} p(\boldsymbol{X}, \boldsymbol{Z}| \boldsymbol{\theta}) &=& p(\boldsymbol{z}_1|\boldsymbol{\pi}) \cdot \left( \prod_{t=2}^T p(\boldsymbol{z}_t|\boldsymbol{z}_{t-1}, \boldsymbol{A}) \right) \cdot \prod_{\tau=1}^T p(\boldsymbol{x}_\tau|\boldsymbol{z}_\tau, \boldsymbol{\phi}) \label{eq: seq HMM 1 sequence joint prob} \end{eqnarray}\] เมื่อ \(\boldsymbol{X} = \{\boldsymbol{x}_1, \ldots, \boldsymbol{x}_T\}\), \(\boldsymbol{Z} = \{\boldsymbol{z}_1, \ldots, \boldsymbol{z}_T\}\) และ \(\boldsymbol{\theta} = \{ \boldsymbol{\pi}, \boldsymbol{A}, \boldsymbol{\phi} \}\) เป็นชุดพารามิเตอร์ทั้งหมดของแบบจำลอง.
จากแบบจำลองในสมการ \(\eqref{eq: seq HMM 1 sequence joint prob}\) เป็นแบบจำลองสร้างกำเนิด (generative model) ซึ่งด้วยทฤษฎีความน่าจะเป็น โดยเฉพาะทฤษฎีของเบส์ (หัวข้อ [sec: cond prob]) เราสามารถทำการอนุมานต่าง ๆ ได้หากรู้ค่าของชุดพารามิเตอร์ \(\boldsymbol{\theta}\) เช่น กรณีการทำนายข้อมูลการเงิน การทายค่าลำดับต่อไป \(\hat{\boldsymbol{x}}_{T+1}\) ก็สามารถอนุมานจาก 5 \(\hat{\boldsymbol{x}}_{T+1} \approx E[\boldsymbol{x}_{T+1}|\boldsymbol{X}, \boldsymbol{\theta}]\) \(=\sum_d \sum_k \sum_j \boldsymbol{x}_{T+1,d} \cdot p(\boldsymbol{x}_{T+1,d}|\boldsymbol{z}_{T+1, k}, \boldsymbol{\phi}) \cdot p(\boldsymbol{z}_{T+1, k}|\boldsymbol{z}_{T,j}, \boldsymbol{A}) \cdot p((\boldsymbol{z}_{T,j}|\boldsymbol{X}, \boldsymbol{\theta})\) และ \(p((\boldsymbol{z}_T|\boldsymbol{X}, \boldsymbol{\theta}) = \sum_{\{\boldsymbol{z}_1, \ldots, \boldsymbol{z}_{T-1}\}} p(\boldsymbol{Z}|\boldsymbol{X}, \boldsymbol{\theta})\) โดย \(p(\boldsymbol{Z}|\boldsymbol{X}, \boldsymbol{\theta}) = \frac{p(\boldsymbol{X}, \boldsymbol{Z}|\boldsymbol{\theta})}{\sum_{\boldsymbol{Z}} p(\boldsymbol{X},\boldsymbol{Z}|\boldsymbol{\theta})}\).
8.3.1 การฝึกแบบจำลองมาร์คอฟซ่อนเร้น
การฝึกแบบจำลองมาร์คอฟซ่อนเร้น หรือการหาค่าชุดพารามิเตอร์ \(\boldsymbol{\theta}\) สามารถทำได้ด้วยวิธีค่าฟังก์ชันควรจะเป็นสูงสุด (maximum likelihood ดูแบบฝึกหัด [ex: ann predicts dists]). แนวคิดของวิธีค่าฟังก์ชันควรจะเป็นสูงสุด คือ การหาค่าของชุดพารามิเตอร์ ที่ทำให้ค่าความน่าจะเป็นภายหลัง (posterior) มีค่ามากกว่าที่สุด โดยความน่าจะเป็นภายหลัง คือค่าความน่าจะเป็นที่คำนวณด้วยค่าต่าง ๆ ของชุดข้อมูลที่มีอยู่.
นั่นคือ ด้วยข้อมูลชุดลำดับ \(\boldsymbol{X} = \{\boldsymbol{x}_1, \ldots, \boldsymbol{x}_T\}\) ที่สังเกตได้ ค่าค่าของชุดพารามิเตอร์ \(\boldsymbol{\theta}\) ของแบบจำลองมาร์คอฟซ่อนเร้น สามารถหาได้จาก \(\boldsymbol{\theta}^\ast = \arg\max_{\boldsymbol{\theta}} p(\boldsymbol{X}|\boldsymbol{\theta})\) โดย \(p(\boldsymbol{X}|\boldsymbol{\theta})\) อาจหาได้โดยการสลายปัจจัย (marginalization) \[\begin{eqnarray} p(\boldsymbol{X}|\boldsymbol{\theta}) &=& \sum_{\boldsymbol{Z}} p(\boldsymbol{X}, \boldsymbol{Z}|\boldsymbol{\theta}) \label{eq: seq HMM marginal dist}. \end{eqnarray}\]
ในทางปฏิบัติ การคำนวณสมการ \(\eqref{eq: seq HMM marginal dist}\) โดยตรง ทำได้ยาก เพราะว่า การสลายปัจจัย อาศัยการบวกทุกค่าที่เป็นไปได้ของชุดลำดับสถานะซ่อนเร้น \(\boldsymbol{Z} = \{\boldsymbol{z}_1, \ldots, \boldsymbol{z}_T\}\) และ ที่แต่ละลำดับ สถานะซ่อนเร้นก็มีโอกาสเป็นไปได้หลายค่า. ในที่นี้ กำหนดให้ ค่าของสถานะซ่อนเร้นที่เป็นไปได้ มีจำนวนเป็น \(K\) ค่า. ด้วยความยาวของลำดับเป็น \(T\) ทำให้มีชุดค่าของลำดับสถานะซ่อนเร้นที่เป็นไปได้เท่ากับ \(K^T\) ชุด. จำนวนพจน์ที่ต้องทำการบวก จะเพิ่มขึ้นแบบชี้กำลังตามความยาวของชุดลำดับ.
แนวทางหนึ่งสามารถนำมาใช้คำนวณหาค่าพารามิเตอร์ที่เหมาะสมได้ คือ ขั้นตอนวิธีอีเอ็ม (expectation-maximization algorithm คำย่อ EM algorithm) ซึ่งเป็นขั้นตอนวิธีทั่ว ๆ ไปสำหรับการหาค่าพารามิเตอร์ของแบบจำลอง โดยมีนัยของความน่าจะเป็นประกอบ. กล่าวโดยคร่าว ๆ ขั้นตอนวิธีอีเอ็ม อาศัยการทำงานเป็นสองขั้นตอนหลัก ๆ คือ ขั้นตอนการหาค่าคาดหมาย (expectation phase) และขั้นตอนการหาค่าตัวทำมากที่สุด (maximization phase). ขั้นตอนวิธีอีเอ็ม เริ่มด้วยค่าเริ่มต้นของพารามิเตอร์ \(\boldsymbol{\theta}_0\) แล้วคำนวณความน่าจะเป็นภายหลัง \(p(\boldsymbol{Z}|\boldsymbol{X}, \boldsymbol{\theta}_0)\). จากนั้น ใช้ค่าความน่าจะเป็นภายหลังที่ได้ เพื่อประเมินค่าคาดหมายของลอการิทึมของค่าฟังก์ชันควรจะเป็นของข้อมูล \[\begin{eqnarray} \varepsilon (\boldsymbol{\theta}, \boldsymbol{\theta}_0) &=& \sum_{\boldsymbol{Z}} p(\boldsymbol{Z}|\boldsymbol{X}, \boldsymbol{\theta}_0) \cdot \ln p(\boldsymbol{X},\boldsymbol{Z}|\boldsymbol{\theta}) \label{eq: seq HMM likelihood function} \end{eqnarray}\] เมื่อ \(\boldsymbol{\theta}_0\) เป็นค่าพารามิเตอร์ ณ ปัจจุบัน ส่วน \(\boldsymbol{\theta}\) เป็นตัวแปรของค่าพารามิเตอร์ (ที่ต้องการจะปรับปรุงใหม่). การประเมินฟังก์ชันควรจะเป็น \(\varepsilon (\boldsymbol{\theta}, \boldsymbol{\theta}_0)\) จะใช้ในกระบวนการหาค่าพารามิเตอร์ที่ดีที่สุด. หลังจากได้ค่าพารามิเตอร์ชุดใหม่แล้ว จึงวนซ้ำคำนวณในลักษณะเช่นนี้ต่อไป จนค่าต่าง ๆ ลู่เข้า หรือจนกว่าจะเป็นไปตามเงื่อนไขการจบการคำนวณ.
8.3.1.0.1 ขั้นตอนวิธีอีเอ็ม.
กล่าวโดยละเอียดแล้ว ด้วยค่าพารามิเตอร์ \(\boldsymbol{\theta}_0\) ขั้นตอนวิธีอีเอ็ม เริ่มที่ขั้นตอนการหาค่าคาดหมายใช้ค่าพารามิเตอร์นี้ในการคำนวณค่าคาดหมายของสถานะซ่อนเร้น.
เพื่อความสะดวก นิยามความน่าจะเป็นภายหลังของสถานะซ่อนเร้นด้วย \(\boldsymbol{q}_t\) และนิยามความน่าจะเป็นภายหลังร่วมด้วย \(\boldsymbol{R}^{(t-1,t)}\). นั่นคือ \[\begin{eqnarray} \boldsymbol{q}_t &\equiv& p(\boldsymbol{z}_t|\boldsymbol{X}, \boldsymbol{\theta}_0) \label{eq: seq HMM q} \\ \boldsymbol{R}^{(t-1, t)} &\equiv& p(\boldsymbol{z}_{t-1}, \boldsymbol{z}_t|\boldsymbol{X}, \boldsymbol{\theta}_0) \label{eq: seq HMM r} \end{eqnarray}\] โดย สำหรับแต่ละดัชนีลำดับ \(t\) เวกเตอร์ \(\boldsymbol{q}_t \in [0,1]^K\) ซึ่งส่วนประกอบ \(q_{tk} \equiv p(z_{tk} = 1|\boldsymbol{X}, \boldsymbol{\theta}_0)\) และ เมทริกซ์ \(\boldsymbol{R}^{(t-1,t)} \in [0,1]^{K \times K}\) ซึ่งส่วนประกอบ \(R^{(t-1,t)}_{j,k} \equiv p(z_{t-1,j} = 1, z_{t,k}=1|\boldsymbol{X}, \boldsymbol{\theta}_0)\).
หมายเหตุ เนื่องจาก \(z_{tk}\) เป็นตัวแปรค่าทวิภาค นั่นทำให้ ค่าคาดหมายของสถานะซ่อนเร้น \(E[z_{tk}] = p(z_{tk}=1|\boldsymbol{X}, \boldsymbol{\theta}_0) \cdot 1 + p(z_{tk}=0|\boldsymbol{X}, \boldsymbol{\theta}_0) \cdot 0\) \(= p(z_{tk}=1|\boldsymbol{X}, \boldsymbol{\theta}_0)\) \(=q_{tk}\). ในทำนองเดียวกัน \(E[z_{t-1,j} \cdot z_{tk}]\) \(=p(z_{t-1,j} = 1, z_{t,k}=1|\boldsymbol{X}, \boldsymbol{\theta}_0) \cdot 1 \cdot 1 + 0 + 0 + 0\) \(=R^{(t-1,t)}_{j,k}\). ดังนั้น การประมาณค่าความน่าจะเป็นภายหลัง \(\boldsymbol{q}_t\) และความน่าจะเป็นภายหลังร่วม \(\boldsymbol{R}^{(t-1,t)}\) จึงเทียบเท่ากับการหาค่าคาดหมาย. การคำนวณในขั้นตอนนี้ จึงถูกเรียกว่าเป็น ขั้นตอนการหาค่าคาดหมาย.
ด้วยความน่าจะเป็นภายหลังทั้ง \(\boldsymbol{q}_t\) และ \(\boldsymbol{R}^{(t-1,t)}\) และนำแบบจำลองซ่อนเร้น ในสมการ \(\eqref{eq: seq HMM 1 sequence joint prob}\) มาประกอบ เราจะได้ฟังก์ชันควรจะเป็น (สมการ \(\eqref{eq: seq HMM likelihood function}\)) ว่า \[\begin{eqnarray} \varepsilon (\boldsymbol{\theta}, \boldsymbol{\theta}_0) &=& \sum_{\boldsymbol{Z}} p(\boldsymbol{Z}|\boldsymbol{X}, \boldsymbol{\theta}_0) \cdot \ln \left\{p(\boldsymbol{z}_1|\boldsymbol{\pi}) \cdot \left( \prod_{t=2}^T p(\boldsymbol{z}_t|\boldsymbol{z}_{t-1}, \boldsymbol{A}) \right) \cdot \prod_{\tau=1}^T p(\boldsymbol{x}_\tau|\boldsymbol{z}_\tau, \boldsymbol{\phi}) \right\} \nonumber \\ &=& \sum_{k=1}^K q_{1k} \cdot \ln p(\boldsymbol{z}_1|\boldsymbol{\pi}) + \sum_{j=1}^K \sum_{k=1}^K \sum_{t=2}^T R^{(t-1,t)}_{j,k} \cdot \ln p(\boldsymbol{z}_t|\boldsymbol{z}_{t-1}, \boldsymbol{A}) \nonumber\\ &\;& + \sum_{k=1}^K \sum_{\tau=1}^T q_{\tau k} \cdot \ln p(\boldsymbol{x}_\tau|\boldsymbol{z}_\tau, \boldsymbol{\phi}) \nonumber \\ &=& \sum_{k=1}^K q_{1k} \cdot \ln \pi_k + \sum_{j=1}^K \sum_{k=1}^K \sum_{t=2}^T R^{(t-1,t)}_{j,k} \cdot \ln A_{jk} + \sum_{k=1}^K \sum_{\tau=1}^T q_{\tau k} \cdot \ln p(\boldsymbol{x}_\tau|\boldsymbol{\phi}_k) \nonumber \\ \label{eq: seq HMM likelihood function M step} \end{eqnarray}\] โดย \(\boldsymbol{\pi}\) และ \(\boldsymbol{A}\) เป็นค่าความน่าจะเป็นเริ่มต้น และความน่าจะเป็นของการเปลี่ยนสถานะ ตามลำดับ. ส่วน \(p(\boldsymbol{x}_\tau|\boldsymbol{\phi}_k)\) คือความน่าจะเป็นของการปล่อยของสถานะที่ \(k^{th}\).
ขั้นตอนการหาค่าตัวทำมากที่สุด หาค่าของพารามิเตอร์ \(\boldsymbol{\theta} =\{\boldsymbol{\pi}, \boldsymbol{A}, \boldsymbol{\phi} \}\) จากค่าที่ทำให้ฟังก์ชันควรจะเป็น (สมการ \(\eqref{eq: seq HMM likelihood function M step}\)) มีค่ามากที่สุด (โดยค่า \(\boldsymbol{q}_t\) และ \(\boldsymbol{R}^{(t-1,t)}\) จะใช้ค่าที่ได้จากขั้นตอนการหาค่าคาดหมาย และคิดเสมือนเป็นค่าคงที่). ค่าพารามิเตอร์ \(\boldsymbol{\pi}\) และ \(\boldsymbol{A}\) หาได้จากค่าทำมากที่สุดของฟังก์ชันควรจะเป็น ประกอบกับเงื่อนไขของพารามิเตอร์ ได้แก่ \(\sum_k \pi_k = 1\) และ \(\sum_k A_{jk} = 1\) และได้ผลลัพธ์ (ดูแบบฝึกหัด [ex: seq HMM M step derivatives]) คือ \[\begin{eqnarray} \pi_k &=& \frac{q_{1k}}{\sum_{j=1}^K q_{1j}} \label{eq: seq HMM pi_k} \\ A_{jk} &=& \frac{\sum_{t=2}^T R^{(t-1,t)}_{jk} }{ \sum_{l=1}^K \sum_{t=2}^T R^{(t-1,t)}_{jl} } \label{eq: seq HMM A_jk} . \end{eqnarray}\]
สำหรับพารามิเตอร์ \(\boldsymbol{\phi}\) การหาค่าก็สามารถทำได้ในทำนองเดียวกัน เพียงแต่แบบจำลองมาร์คอฟซ่อนเร้น เปิดกว้างสำหรับการเลือกใช้ฟังก์ชันการปล่อย \(p(\boldsymbol{x}_t|\boldsymbol{\phi}_k)\) ได้หลายแบบ.
หากเลือกฟังก์ชันการปล่อยเกาส์เซียน นั่นคือ \(p(\boldsymbol{x}_t|\boldsymbol{\phi}_k)\) \(\equiv \mathcal{N}(\boldsymbol{x}_t|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)\). เมื่อทำการหาค่าตัวทำมากที่สุด ผลลัพธ์จะได้เป็น \[\begin{eqnarray} \boldsymbol{\mu}_k &=& \frac{\sum_{t=1}^T q_{tk} \cdot \boldsymbol{x}_t }{ \sum_{t=1}^T q_{tk} } \label{eq: HMM M step Gaussian mu} \\ \boldsymbol{\Sigma}_k &=& \frac{\sum_{t=1}^T q_{tk} \cdot (\boldsymbol{x}_t - \boldsymbol{\mu}_k) \cdot (\boldsymbol{x}_t - \boldsymbol{\mu}_k)^T }{ \sum_{t=1}^T q_{tk} } \label{eq: HMM M step Gaussian sigma} . \end{eqnarray}\]
หากเลือกฟังก์ชันการปล่อยอเนกนามวิยุต (discrete multinomial emission function) นั่นคือ การกำหนด \(p(\boldsymbol{x}_t|\boldsymbol{\phi}_k)\) \(\equiv \prod_{d=1}^D \phi_{kd}^{x_{td}}\) เมื่อ พารามิเตอร์ \(\phi_{kd}\) แทนค่าความน่าจะเป็นที่จะพบตัวแปรที่ถูกสังเกต \(\boldsymbol{x}_t\) เป็นชนิด \(d^{th}\) หากสถานะซ่อนเร้นเป็นชนิด \(k^{th}\). ค่าของตัวแปรที่ถูกสังเกต \(\boldsymbol{x}_t\) ใช้รหัสหนึ่งร้อน ซึ่งคือ \(\boldsymbol{x}_t = [x_{t1}, \ldots, x_{tD}]^T\) โดย \(D\) คือจำนวนค่าวิยุต ที่ตัวแปรสามารถแทนได้. ส่วนประกอบ \(x_{td} \in \{0,1\}\) และ \(\sum_{d=1}^D x_{td} = 1\). เมื่อทำการหาค่าตัวทำมากที่สุด ผลลัพธ์จะได้เป็น \[\begin{eqnarray} \phi_{kd} &=& \frac{\sum_{t=1}^T q_{tk} \cdot x_{td} }{ \sum_{t=1}^T q_{tk} } \label{eq: HMM M step multinomial phi}. \end{eqnarray}\]
ค่าเริ่มต้นของพารามิเตอร์ \(\boldsymbol{\pi}\) และ \(\boldsymbol{A}\) อาจกำหนดได้โดยการสุ่ม แต่ต้องควบคุมให้ค่าเป็นไปตามเงื่อนไขของความน่าจะเป็น นั่นคือ \(\pi_k \geq 0\), \(\sum_k \pi_k = 1\), \(A_{jk} \geq 0\) และ \(\sum_k A_{jk} = 1\). ค่าเริ่มต้นของพารามิเตอร์ของ \(\boldsymbol{\phi}\) อาจกำหนดเป็นเสมือนพารามิเตอร์อีกส่วน และใช้กระบวนการเรียนรู้จากข้อมูลเพื่อช่วยกำหนดค่าได้.
ขั้นตอนวิธีอีเอ็ม มีคุณสมบัติความถูกต้องและคุณสมบัติการลู่เข้าที่ดี (ดู เพิ่มเติม). อย่างไรก็ตาม ในขั้นตอนการหาค่าคาดหมาย การประมาณค่าของค่าความน่าจะเป็นภายหลัง \(\boldsymbol{q}_t\) และ \(\boldsymbol{R}^{(t-1,t)}\) แม้อาจสามารถทำได้โดยวิธีการสลายปัจจัย เช่น \(\boldsymbol{q}_t\) \(= p(\boldsymbol{z}_t|\boldsymbol{X}, \boldsymbol{\theta}_0)\) \(= \sum_{ \{\boldsymbol{z}_1, \ldots, \boldsymbol{z}_{t-1}, \boldsymbol{z}_{t+1}, \ldots, \boldsymbol{z}_T \} }\) \(p(\boldsymbol{Z}|\boldsymbol{X}, \boldsymbol{\theta}_0)\) และ \(\boldsymbol{R}^{(t-1, t)} = p(\boldsymbol{z}_{t-1}, \boldsymbol{z}_t|\boldsymbol{X}, \boldsymbol{\theta}_0)\) \(= \sum_{ \{\boldsymbol{z}_1, \ldots, \boldsymbol{z}_{t-2}, \boldsymbol{z}_{t+1}, \ldots, \boldsymbol{z}_T \} } p(\boldsymbol{Z}|\boldsymbol{X}, \boldsymbol{\theta}_0)\) โดย \(p(\boldsymbol{Z}|\boldsymbol{X}, \boldsymbol{\theta}_0)\) ก็อาจจะหาได้จากกฎของเบส์ \(p(\boldsymbol{Z}|\boldsymbol{X}, \boldsymbol{\theta}_0)\) \(= p(\boldsymbol{Z},\boldsymbol{X}| \boldsymbol{\theta}_0) / \sum_{\boldsymbol{Z}} p(\boldsymbol{Z},\boldsymbol{X}| \boldsymbol{\theta}_0)\) แต่วิธีนี้ใช้การคำนวณมหาศาล.
เฉพาะการคำนวณ \(\sum_{ \{\boldsymbol{z}_1, \ldots, \boldsymbol{z}_{t-1}, \boldsymbol{z}_{t+1}, \ldots, \boldsymbol{z}_T \} } p(\boldsymbol{Z}|\boldsymbol{X}, \boldsymbol{\theta}_0)\) เองอย่างเดียว ก็เท่ากับต้องบวกพจน์ทั้งหมด \((T-1) \cdot K\) พจน์เข้าด้วยกัน และค่าของแต่ละพจน์ ก็ต้องผ่านการคำนวณต่าง ๆ ดังอภิปราย. ดังนั้น เมื่อต้องนำมาใช้กับขั้นตอนวิธีอีเอ็ม ซึ่งต้องคำนวณค่าความน่าจะเป็นภายหลังใหม่ทุก ๆ สมัยฝึก การประมาณค่า \(\boldsymbol{q}_t\) และ \(\boldsymbol{R}^{(t-1,t)}\) ด้วยวิธีนี้ จึงไม่เหมาะที่จะนำมาใช้ได้ในทางปฏิบัติ.
ปัญหาการคำนวณค่าความน่าจะเป็นภายหลังอย่างมีประสิทธิภาพ ถูกบรรเทาด้วยขั้นตอนวิธีไปข้างหน้ากับถอยกลับ ที่จะอภิปรายต่อไปในหัวข้อ 1.3.2.
8.3.2 ขั้นตอนวิธีไปข้างหน้ากับถอยกลับ
ขั้นตอนวิธีไปข้างหน้ากับถอยกลับ (forward-backward algorithm) เป็นขั้นตอนวิธี ที่ใช้คำนวณค่าของความน่าจะเป็นภายหลังที่ใช้ในวิธีอีเอ็ม ได้อย่างมีประสิทธิภาพ. จริง ๆ แล้ว ขั้นตอนวิธีไปข้างหน้ากับถอยกลับ มีการศึกษาอย่างกว้าง และวิธีดำเนินการก็มีอยู่หลายแบบ หัวข้อนี้จะอภิปรายแบบหนึ่งที่มีการใช้อย่างกว้างขวาง เรียกว่า ขั้นตอนวิธีแอลฟา-บีตา (alpha-beta algorithm). เนื่องจาก หัวข้อนี้พิจารณาค่าพารามิเตอร์ \(\boldsymbol{\theta}_0\) เป็นเสมือนค่าคงที่ ดังนั้นเงื่อนไข \(\boldsymbol{\theta}_0\) จะถูกละไว้ในฐานที่เข้าใจ เพื่อความกระชับ.
ด้วยเงื่อนไขของแบบจำลองมาร์คอฟซ่อนเร้น ระบบจะมีคุณสมบัติดังนี้ \[\begin{eqnarray} p(\boldsymbol{X}|\boldsymbol{z}_t) &=& p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_t|\boldsymbol{z}_t) \cdot p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T|\boldsymbol{z}_t) \label{eq: alpha-beta prelude property 1} \\ p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{z}_t) &=& p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_{t-1}|\boldsymbol{z}_t) \label{eq: alpha-beta prelude property 2} \\ p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_{t-1}|\boldsymbol{z}_{t-1}, \boldsymbol{z}_t) &=& p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_{t-1}|\boldsymbol{z}_{t-1}) \label{eq: alpha-beta prelude property 3} \\ p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T|\boldsymbol{z}_t, \boldsymbol{z}_{t+1}) &=& p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T|\boldsymbol{z}_{t+1}) \label{eq: alpha-beta prelude property 4} \\ p(\boldsymbol{x}_{t+2}, \ldots, \boldsymbol{x}_T|\boldsymbol{x}_{t+1}, \boldsymbol{z}_{t+1}) &=& p(\boldsymbol{x}_{t+2}, \ldots, \boldsymbol{x}_T|\boldsymbol{z}_{t+1}) \label{eq: alpha-beta prelude property 5} \\ p(\boldsymbol{X}|\boldsymbol{z}_{t-1}, \boldsymbol{z}_{t}) &=& p(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{t-1}|\boldsymbol{z}_{t-1}) \cdot p(\boldsymbol{x}_t|\boldsymbol{z}_t) \cdot p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_{T}|\boldsymbol{z}_{t}) \nonumber \\ \label{eq: alpha-beta prelude property 6} \\ p(\boldsymbol{x}_{T+1}|\boldsymbol{X}, \boldsymbol{z}_{T+1}) &=& p(\boldsymbol{x}_{T+1}|\boldsymbol{z}_{T+1}) \label{eq: alpha-beta prelude property 7} \\ p(\boldsymbol{z}_{T+1}|\boldsymbol{X}, \boldsymbol{z}_{T+1}) &=& p(\boldsymbol{z}_{T+1}|\boldsymbol{z}_{T+1}) \label{eq: alpha-beta prelude property 8} \end{eqnarray}\] เมื่อ \(\boldsymbol{X} = \{ \boldsymbol{x}_1, \ldots, \boldsymbol{x}_T \}\).
พิจารณา \[\begin{eqnarray} \boldsymbol{q}_t &=& p(\boldsymbol{z}_t|\boldsymbol{X}) = \frac{p(\boldsymbol{X}|\boldsymbol{z}_t) \cdot p(\boldsymbol{z}_t)}{p(\boldsymbol{X})} \label{eq: alpha-beta q}. \end{eqnarray}\]
ด้วยสมการ \(\eqref{eq: alpha-beta prelude property 1}\) และกฎผลคูณ เราจะได้ \[\begin{eqnarray} \boldsymbol{q}_t &=& \frac{p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_t,\boldsymbol{z}_t) \cdot p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T|\boldsymbol{z}_t)}{p(\boldsymbol{X})} = \frac{\alpha(\boldsymbol{z}_t) \cdot \beta(\boldsymbol{z}_t) }{p(\boldsymbol{X})} \label{eq: alpha-beta q alpha beta} \end{eqnarray}\] โดยนิยาม \[\begin{eqnarray} \alpha(\boldsymbol{z}_t) & \equiv & p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_t, \boldsymbol{z}_t) \label{eq: alpha-beta alpha} \\ \beta(\boldsymbol{z}_t) & \equiv & p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T| \boldsymbol{z}_t) \label{eq: alpha-beta beta}. \end{eqnarray}\]
ค่า \(\alpha(\boldsymbol{z}_t) \in \mathbb{R}^K\) แทนค่าความน่าจะเป็นร่วม ระหว่างข้อมูลชุดลำดับที่สังเกตจนถึงเวลา \(t\) กับสถานะซ่อนเร้นของเวลา \(t\). ค่า \(\beta(\boldsymbol{z}_t) \in \mathbb{R}^K\) แทนค่าความน่าจะเป็นแบบมีเงื่อนไขของข้อมูลชุดลำดับที่สังเกตตั้งแต่เวลา \(t\) ไปจนจบ เมื่อมีสถานะซ่อนเร้นที่เวลา \(t\) เป็นเงื่อนไข. เพื่อความสะดวก กำหนดให้ \(\alpha(z_{tk}) \equiv p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_t, z_{tk}=1)\) และ \(\beta(\boldsymbol{z}_t) \equiv p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T| z_{tk}=1)\) โดย \(\boldsymbol{z}_t\) แสดงด้วยรหัสหนึ่งร้อน.
ในทำนองเดียวกัน \[\begin{eqnarray} \boldsymbol{R}^{(t-1, t)} &=& p(\boldsymbol{z}_{t-1}, \boldsymbol{z}_t | \boldsymbol{X}) = \frac{p(\boldsymbol{X}|\boldsymbol{z}_{t-1}, \boldsymbol{z}_t) \cdot p(\boldsymbol{z}_{t-1}, \boldsymbol{z}_t)}{p(\boldsymbol{X})} \nonumber \\ &=& \frac{ p(\boldsymbol{x}_1, \ldots,\boldsymbol{x}_{t-1}|\boldsymbol{z}_{t-1}) \cdot p(\boldsymbol{x}_t|\boldsymbol{z}_t) \cdot p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T|\boldsymbol{z}_t) \cdot p(\boldsymbol{z}_t| \boldsymbol{z}_{t-1}) \cdot p(\boldsymbol{z}_{t-1}) }{p(\boldsymbol{X})} \nonumber \\ &=& \frac{ \alpha(\boldsymbol{z}_{t-1}) \cdot p(\boldsymbol{x}_t|\boldsymbol{z}_t) \cdot \beta(\boldsymbol{z}_t) \cdot p(\boldsymbol{z}_t| \boldsymbol{z}_{t-1}) }{p(\boldsymbol{X})} \label{eq: alpha-beta R alpha beta}. \end{eqnarray}\]
แนวคิดของขั้นตอนวิธีไปข้างหน้ากับถอยกลับ คือ จัดรูปการคำนวณ \(\alpha(\boldsymbol{z}_t)\) และ \(\beta(\boldsymbol{z}_t)\) ให้อยู่ในรูปที่สามารถคำนวณได้อย่างมีประสิทธิภาพ โดยอาศัยความสัมพันธ์แบบเรียกซ้ำ (recursive relation). การคำนวณค่า \(\alpha(\boldsymbol{z}_t)\) สามารถจัดรูปใหม่ได้ดังนี้ \[\begin{eqnarray} \alpha(\boldsymbol{z}_t) &=& p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_t, \boldsymbol{z}_t) \nonumber \\ &=& p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_t| \boldsymbol{z}_t) \cdot p(\boldsymbol{z}_t) \nonumber \\ &=& p(\boldsymbol{x}_t|\boldsymbol{z}_t) \cdot p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_{t-1}| \boldsymbol{z}_t) \cdot p(\boldsymbol{z}_t) \nonumber \\ &=& p(\boldsymbol{x}_t|\boldsymbol{z}_t) \cdot p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_{t-1}, \boldsymbol{z}_t) \nonumber \\ &=& p(\boldsymbol{x}_t|\boldsymbol{z}_t) \cdot \sum_{\boldsymbol{z}_{t-1}} p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_{t-1}, \boldsymbol{z}_{t-1}, \boldsymbol{z}_t) \nonumber \\ &=& p(\boldsymbol{x}_t|\boldsymbol{z}_t) \cdot \sum_{\boldsymbol{z}_{t-1}} p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_{t-1}, \boldsymbol{z}_t| \boldsymbol{z}_{t-1}) \cdot p(\boldsymbol{z}_{t-1}) \nonumber \\ &=& p(\boldsymbol{x}_t|\boldsymbol{z}_t) \cdot \sum_{\boldsymbol{z}_{t-1}} p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_{t-1}| \boldsymbol{z}_{t-1}) \cdot p(\boldsymbol{z}_t|\boldsymbol{z}_{t-1}) \cdot p(\boldsymbol{z}_{t-1}) \nonumber \\ &=& p(\boldsymbol{x}_t|\boldsymbol{z}_t) \cdot \sum_{\boldsymbol{z}_{t-1}} p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_{t-1}, \boldsymbol{z}_{t-1}) \cdot p(\boldsymbol{z}_t|\boldsymbol{z}_{t-1}) \nonumber \\ &=& p(\boldsymbol{x}_t|\boldsymbol{z}_t) \cdot \sum_{\boldsymbol{z}_{t-1}} \alpha(\boldsymbol{z}_{t-1}) \cdot p(\boldsymbol{z}_t|\boldsymbol{z}_{t-1}) \label{eq: HMM alpha-beta alpha} \end{eqnarray}\] สำหรับ \(t = 2, \ldots, T\). \[\begin{eqnarray} \alpha(\boldsymbol{z}_1) &=& p(\boldsymbol{x}_1, \boldsymbol{z}_1) = p(\boldsymbol{z}_1) \cdot p(\boldsymbol{x}_1|\boldsymbol{z}_1) = \prod_{k=1}^K \left( \pi_k \cdot p(\boldsymbol{x}_1|\boldsymbol{\phi}_k) \right)^{z_{1k}} \label{eq: HMM alpha-beta alpha t1}. \end{eqnarray}\] นั่นคือ \(\alpha( z_{1k} ) = \pi_k \cdot p(\boldsymbol{x}_1|\boldsymbol{\phi}_k)\).
การคำนวณเริ่มจากลำดับเวลาแรก แล้วค่อย ๆ คำนวณขยับไปทีละลำดับ. การคำนวณสมการ \(\eqref{eq: HMM alpha-beta alpha}\) ทำการบวก \(K\) พจน์ สำหรับแต่ละสถานะซ่อนเร้น ซึ่งสถานะซ่อนเร้นมีจำนวนทั้งหมด \(K\) สถานะ. ดังนั้นที่แต่ละลำดับเวลา การคำนวณจะขยายเป็น \(K^2\) (นั่นคือ \(O(K^2)\)) และการคำนวณจะเป็น \(O(T K^2)\) สำหรับทั้งชุดลำดับ.
ในทำนองเดียวกัน ค่า \(\beta(\boldsymbol{z}_t)\) สามารถจัดรูปการคำนวณใหม่ได้ดังนี้ \[\begin{eqnarray} \beta(\boldsymbol{z}_t) &=& p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T|\boldsymbol{z}_t) \nonumber \\ &=& \sum_{\boldsymbol{z}_{t+1}} p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T, \boldsymbol{z}_{t+1}|\boldsymbol{z}_t) \nonumber \\ &=& \sum_{\boldsymbol{z}_{t+1}} p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T|\boldsymbol{z}_{t+1},\boldsymbol{z}_t)) \cdot p(\boldsymbol{z}_{t+1}|\boldsymbol{z}_t) \nonumber \\ &=& \sum_{\boldsymbol{z}_{t+1}} p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T|\boldsymbol{z}_{t+1})) \cdot p(\boldsymbol{z}_{t+1}|\boldsymbol{z}_t) \nonumber \\ &=& \sum_{\boldsymbol{z}_{t+1}} p(\boldsymbol{x}_{t+2}, \ldots, \boldsymbol{x}_T|\boldsymbol{z}_{t+1})) \cdot p(\boldsymbol{x}_{t+1}|\boldsymbol{z}_{t+1}) \cdot p(\boldsymbol{z}_{t+1}|\boldsymbol{z}_t) \nonumber \\ &=& \sum_{\boldsymbol{z}_{t+1}} \beta(\boldsymbol{z}_{t+1}) \cdot p(\boldsymbol{x}_{t+1}|\boldsymbol{z}_{t+1}) \cdot p(\boldsymbol{z}_{t+1}|\boldsymbol{z}_t) \label{eq: HMM alpha-beta beta} \end{eqnarray}\] สำหรับ \(t = 1, \ldots, T-1\). สำหรับ ลำดับเวลาท้ายสุด เพื่อประเมินค่า \(\beta(\boldsymbol{z}_T)\) พิจารณาสมการ \(\eqref{eq: alpha-beta q}\) และ \(\eqref{eq: alpha-beta q alpha beta}\) เมื่อ \(t = T\). นั่นคือ \[\begin{eqnarray} p(\boldsymbol{z}_T|\boldsymbol{X}) &=& \frac{p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_T,\boldsymbol{z}_T) \cdot \beta(\boldsymbol{z}_T) }{p(\boldsymbol{X})} = \frac{p(\boldsymbol{X}, \boldsymbol{z}_T)}{p(\boldsymbol{X})} \cdot \beta(\boldsymbol{z}_T) \end{eqnarray}\] และจากกฎผลคูณ ซึ่ง ณ ที่นี้ คือ \(\frac{p(\boldsymbol{X}, \boldsymbol{z}_T)}{p(\boldsymbol{X})} = p(\boldsymbol{z}_T|\boldsymbol{X})\) ดังนั้น ค่าของ \(\beta(\boldsymbol{z}_T)\) ต้องเท่ากับหนึ่ง สำหรับทุก ๆ สถานะของ \(\boldsymbol{z}_T\). นั่นคือ \(\beta(z_{Tk}) = 1\) สำหรับ \(k = 1, \ldots, K\). (หมายเหตุ นิยาม \(\beta(\boldsymbol{z}_t) \equiv p(\boldsymbol{x}_{t+1}, \ldots, \boldsymbol{x}_T| \boldsymbol{z}_t)\) ในนิพจน์ \(\eqref{eq: alpha-beta beta}\) ไม่ได้ครอบคลุมลำดับ \(t = T\).)
ตรงกันข้ามกับการคำนวณ \(\alpha(\boldsymbol{z}_t)\) ที่เริ่มจากลำดับเวลาแรก แล้วขยับลำดับไปข้างหน้า การคำนวณ \(\beta(\boldsymbol{z}_t)\) เริ่มจากลำดับเวลาท้ายสุด แล้วขยับย้อนถอยหลังมาเรื่อย ๆ. หลังจากได้ค่าของ \(\alpha(\boldsymbol{z}_t)\) และ \(\beta(\boldsymbol{z}_t)\) สำหรับ \(t = 1, \ldots, T\) แล้วอาจประเมินค่าความน่าจะเป็นภายหลังด้วยสมการ \(\eqref{eq: alpha-beta q alpha beta}\) และ \(\eqref{eq: alpha-beta R alpha beta}\) ในขั้นตอนการหาค่าคาดหมาย ซึ่งต้องการค่า \(p(\boldsymbol{X})\) ประกอบ หรือ อาจนำค่า \(\alpha(\boldsymbol{z}_t)\) และ \(\beta(\boldsymbol{z}_t)\) ที่ได้ ไปใช้ในขั้นตอนการหาค่าตัวทำมากที่สุดโดยตรงเลยก็ได้ เนื่องจากการคำนวณในขั้นตอนการหาค่าตัวทำมากที่สุดนั้น ค่าของ \(p(\boldsymbol{X})\) จะหักล้างกันเอง ตัวอย่างเช่น สมการ \(\eqref{eq: seq HMM pi_k}\) ซึ่งคือ \[\begin{eqnarray} \pi_k &=& \frac{q_{1k}}{\sum_{j=1}^K q_{1j}} = \frac{\alpha(z_{1k}) \cdot \beta(z_{1k})}{\sum_{j=1}^K \alpha(z_{1j}) \cdot \beta(z_{1j})} \label{eq: seq HMM pi_k alpha beta} . \end{eqnarray}\]
อย่างไรก็ตาม หากต้องการประเมินค่าของ \(p(\boldsymbol{X})\) ก็สามารถทำได้อย่างสะดวก. พิจารณาสมการ \(\eqref{eq: alpha-beta q}\) และสมการ \(\eqref{eq: alpha-beta q alpha beta}\) จะเห็นว่า \[\begin{eqnarray} p(\boldsymbol{z}_t|\boldsymbol{X}) &=& \frac{\alpha(\boldsymbol{z}_t) \cdot \beta(\boldsymbol{z}_t)}{p(\boldsymbol{X})} \nonumber \\ p(\boldsymbol{z}_t, \boldsymbol{X}) &=& \alpha(\boldsymbol{z}_t) \cdot \beta(\boldsymbol{z}_t) \nonumber \end{eqnarray}\] ดังนั้น \[\begin{eqnarray} p(\boldsymbol{X}) = \sum_{\boldsymbol{z}_t} p(\boldsymbol{z}_t, \boldsymbol{X}) = \sum_{\boldsymbol{z}_t} \alpha(\boldsymbol{z}_t) \cdot \beta(\boldsymbol{z}_t) \label{eq: alpha beta p(X) any t} \end{eqnarray}\] ซึ่งหมายถึง เราสามารถเลือกดัชนีลำดับ \(t\) ใดก็ได้ ที่จะใช้ประเมินค่า \(p(\boldsymbol{X})\). ค่าดัชนีลำดับที่สะดวกในกรณีนี้ คือ \(t = T\) ซึ่งจะได้ \[\begin{eqnarray} p(\boldsymbol{X}) &=& \sum_{\boldsymbol{z}_T} \alpha(\boldsymbol{z}_T) \label{eq: alpha beta p(X)} \end{eqnarray}\] เพราะว่า \(\beta(\boldsymbol{z}_{tk}) = 1\) สำหรับทุก ๆ ค่าของ \(k\).
สังเกตว่า ค่า \(p(\boldsymbol{X})\) อาจหาได้โดยการสลายปัจจัย \(p(\boldsymbol{X}) = \sum_{\boldsymbol{Z}} p(\boldsymbol{Z}, \boldsymbol{X})\) แต่การทำเช่นนั้นเท่ากับการบวกของ \(K^T\) พจน์ ซึ่งแต่ละพจน์ต้องประเมินค่า \(p(\boldsymbol{Z}, \boldsymbol{X})\) เปรียบเทียบกับสมการ \(\eqref{eq: alpha beta p(X)}\) ซึงเท่ากับการบวกของ \(K\) พจน์เท่านั้น. การจัดรูปการคำนวณในสมการ \(\eqref{eq: alpha beta p(X)}\) จึงเปลี่ยนการคำนวณที่ปริมาณเป็นสัดส่วนเติบโตแบบชี้กำลัง มาเป็นสัดส่วนแบบเชิงเส้น ลดการคำนวณลงได้มหาศาล โดยเฉพาะกับชุดลำดับข้อมูลยาว ๆ.
8.3.2.0.1 การอนุมานข้อมูลด้วยแบบจำลองมาร์คอฟซ่อนเร้น.
แบบจำลองมาร์คอฟซ่อนเร้น สามารถนำประยุกต์ใช้ได้กว้างขวางในการอนุมานต่าง ๆ. ตัวอย่างหนึ่งที่สำคัญ คือ กรณีการอนุมานจุดข้อมูลต่อไปในชุดลำดับ เช่น ในกรณีการทำนายทางการเงิน (ภาพบนสุด รูป 1.1 ที่อินพุตเป็นชุดลำดับของราคาปิดต่อวัน จากหลาย ๆ วันที่ผ่านมา และเอาต์พุตคือค่าทำนายราคาปิดของวันปัจจุบัน). นั่นคือ ด้วยข้อมูลชุดลำดับที่ถูกสังเกตมา \(\boldsymbol{X} = \{\boldsymbol{x}_1, \ldots, \boldsymbol{x}_T \}\) เราต้องการทำนายจุดข้อมูล \(\boldsymbol{x}_{T+1}\). ด้วยเงื่อนไขมาร์คอฟและทฤษฎีของเบส์ การอนุมานอาจทำผ่านค่าความน่าจะเป็น ซึ่งวิเคราะห์ได้ดังนี้ \[\begin{eqnarray} p(\boldsymbol{x}_{T+1}|\boldsymbol{X}) &=& \sum_{\boldsymbol{z}_{T+1}} p(\boldsymbol{x}_{T+1}, \boldsymbol{z}_{T+1}|\boldsymbol{X}) \nonumber \\ &=& \sum_{\boldsymbol{z}_{T+1}} p(\boldsymbol{x}_{T+1}|\boldsymbol{z}_{T+1}) \cdot p(\boldsymbol{z}_{T+1}|\boldsymbol{X}) \nonumber \\ &=& \sum_{\boldsymbol{z}_{T+1}} \left\{ p(\boldsymbol{x}_{T+1}|\boldsymbol{z}_{T+1}) \cdot \sum_{\boldsymbol{z}_T} p(\boldsymbol{z}_T, \boldsymbol{z}_{T+1}|\boldsymbol{X}) \right\} \nonumber \\ &=& \sum_{\boldsymbol{z}_{T+1}} \left\{ p(\boldsymbol{x}_{T+1}|\boldsymbol{z}_{T+1}) \cdot \sum_{\boldsymbol{z}_T} p(\boldsymbol{z}_{T+1}|\boldsymbol{z}_T) \cdot p(\boldsymbol{z}_T|\boldsymbol{X}) \right\} \nonumber \\ &=& \sum_{\boldsymbol{z}_{T+1}} \left\{ p(\boldsymbol{x}_{T+1}|\boldsymbol{z}_{T+1}) \cdot \sum_{\boldsymbol{z}_T} p(\boldsymbol{z}_{T+1}|\boldsymbol{z}_T) \cdot \frac{p(\boldsymbol{z}_T,\boldsymbol{X})}{p(\boldsymbol{X})} \right\} \nonumber \\ &=& \frac{1}{p(\boldsymbol{X})} \sum_{\boldsymbol{z}_{T+1}} \left\{ p(\boldsymbol{x}_{T+1}|\boldsymbol{z}_{T+1}) \cdot \sum_{\boldsymbol{z}_T} p(\boldsymbol{z}_{T+1}|\boldsymbol{z}_T) \cdot \alpha(\boldsymbol{z}_T) \right\} \label{eq: alpha-beta predict next x} . \end{eqnarray}\]
สมการ \(\eqref{eq: alpha-beta predict next x}\) ประเมินได้ ด้วยการบวก \(K^2\) พจน์. การคำนวณสามารถทำได้อย่างมีประสิทธิภาพเช่นนี้ได้ เพราะการประเมินค่า \(p(\boldsymbol{z}_t|\boldsymbol{X})\) สามารถทำผ่านค่า \(\alpha(\boldsymbol{z}_t)\) ได้.
8.3.2.0.2 ข้อจำกัดของแบบจำลองมาร์คอฟซ่อนเร้น.
แบบจำลองมาร์คอฟซ่อนเร้น เป็นแบบจำลองเชิงความน่าจะเป็น แม้จะมีศักยภาพสูง แต่ปัจจุบัน การประยุกต์ใช้กับภาระกิจการรู้จำรูปแบบเชิงลำดับที่ซับซ้อน เช่น การรู้จำเสียงพูด และการประมวลผลภาษาธรรมชาติ นิยมใช้แนวทางของโครงข่ายประสาทเวียนกลับ (หัวข้อ [sec: RNN]) มากกว่า เพราะว่า โครงข่ายประสาทเวียนกลับสามารถทำภาระกิจดังกล่าวได้ดีกว่ามาก. ปัจจัยที่เป็นสาเหตุของความสามารถที่จำกัดของแบบจำลองมาร์คอฟซ่อนเร้น อาจได้แก่ จำนวนสถานะซ่อนเร้น ถูกจำกัด หรือการที่ต้องกำหนด ระบุจำนวนสถานะอย่างชัดเจนในตัวแบบจำลอง, การเรียนรู้ความสัมพันธ์ระยะยาว ต้องการอาศัยการทำผ่านตัวแปรซ่อนเร้น ซึ่งถูกจำกัดจำนวนสถานะไว้ และการใช้รหัสหนึ่งร้อน ยังทำให้ตัวแปรซ่อนเร้นไม่อาจแทนความสัมพันธ์ที่ซับซ้อนอย่างมีประสิทธิภาพได้ คือ ไม่สามารถระบุแยกความสัมพันธ์เป็นองค์ประกอบย่อยได้ และอาจจะรวมถึง การอาศัยมุมมองเชิงความน่าจะเป็น ซึ่งอยู่บนสมมติฐานของการวิเคราะห์ที่ครอบคลุมทุกกรณี ที่อาจจะส่งผลในทางปฏิบัติ (หากไม่มีกลไกพิเศษ เพื่อแก้ไข ชดเชย หรือบรรเทาการคำนวณที่พัฒนาจากสมมติฐานเช่นนี้ 6 ).
8.4 อภิธานศัพท์
- ข้อมูลเชิงลำดับ (sequential data):
ข้อมูลประเภทที่จุดข้อมูลมีความสัมพันธ์เชิงลำดับระหว่างกัน
- แบบจำลองมาร์คอฟ (Markov model):
แบบจำลองความสัมพันธ์เชิงลำดับของข้อมูล ที่ใช้เงื่อนไข ซึ่งจำกัด ให้จุดข้อมูลมีความความสัมพันธ์เชิงความไม่เป็นอิสระต่อกันแบบมีเงื่อนไข (conditional dependence) ระหว่างกันได้ เฉพาะกับจุดข้อมูลลำดับที่ผ่านมา ตามจำนวนลำดับที่กำหนด.
- แบบจำลองมาร์คอฟซ่อนเร้น (Hidden Markov model คำย่อ HMM):
แบบจำลองสำหรับข้อมูลเชิงลำดับ ที่บรรยายความสัมพันธ์เชิงลำดับของค่าข้อมูล ผ่านตัวแปรซ่อนเร้น และใช้เงื่อนไขมาร์คอฟกับตัวแปรซ่อนเร้น.
- ตัวแปรที่สังเกตได้ (observable variable):
ค่าจุดข้อมูล ซึ่งเป็นค่าที่สามารถรู้แน่นอนได้
- สถานะซ่อนเร้น (latent state) หรือ ตัวแปรซ่อนเร้น (latent variable):
ค่าจุดข้อมูลที่สมมติขึ้น หรือเชื่อว่ามีอยู่ อาจจะสามารถรู้ค่าแน่นอนได้ หรืออาจจะไม่สามารถรู้ค่าได้เลย และอาจมีนัยความหมายจริงก็ได้ หรืออาจจะไม่ได้มีนัยความหมายที่ชัดเจนก็ได้.
- ค่าความน่าจะเป็นเริ่มต้น (initial probabilities):
ความน่าจะเป็นของสถานะต่าง ๆ ของจุดข้อมูลที่ลำดับแรกสุด
- ความน่าจะเป็นของการเปลี่ยนสถานะ (transition probabilities):
ความน่าจะเป็นของสถานะต่าง ๆ ของจุดข้อมูลที่ลำดับถัดไป เมื่อจุดข้อมูลลำดับปัจจุบันมีสถานะดังระบุ.
- ความน่าจะเป็นของการปล่อย (emission probabilities):
ความน่าจะเป็นของค่าจุดข้อมูลที่สังเกตได้ เมื่อสถานะซ่อนเร้นมีค่าดังระบุ
- ฟังก์ชันควรจะเป็น (likelihood function):
ฟังก์ชันของตัวแปรที่สนใจ ที่คำนวณค่าความน่าจะเป็น ด้วยค่าข้อมูลที่สังเกตได้
- ขั้นตอนวิธีอีเอ็ม (expectation-maximization algorithm คำย่อ EM algorithm):
ขั้นตอนวิธีทั่ว ๆ ไป สำหรับการหาค่าพารามิเตอร์ ของแบบจำลองเชิงความน่าจะเป็น โดยอาศัยขั้นตอนการคำนวณค่าคาดหมาย เมื่อกำหนดค่าพารามิเตอร์ที่สนใจเป็นค่าคงที่ สลับกับขั้นตอนการหาค่ามากที่สุด ที่ใช้ค่าคาดหมายที่ได้ประเมินค่าฟังก์ชันควรจะเป็น สำหรับการหาค่าพารามิเตอร์ที่ทำให้ฟังก์ชันควรจะเป็นมีค่ามากที่สุด.