7 การเรียนรู้เชิงลึกในโลกการรู้จำทัศนรูปแบบ
“By three methods we may learn wisdom. First, it is by reflection, which is noblest. Second, it is by imitation, which is easiest. And, third, it is by experience, which is the bitterest.”
—Confucius
“มีสามวิธีที่เราจะเรียนรู้. หนึ่ง ด้วยการคิดพิจารณา ซึ่งสูงส่งที่สุด. สอง ด้วยการเลียนแบบ ซึ่งง่ายที่สุด. สาม ด้วยประสบการณ์ ซึ่งขมขื่นที่สุด.”
—ขงจื้อ
โครงข่ายคอนโวลูชั่น เหมาะกับข้อมูลที่มีลักษณะเชิงท้องถิ่นสูง. ในทางปฎิบัติ ข้อมูลหลาย ๆ ชนิด มีลักษณะเชิงท้องถิ่นสูง รวมถึงข้อมูลเชิงทัศนะ เช่น ภาพ และวิดีโอ. โครงข่ายคอนโวลูชั่นได้รับการประยุกต์ใช้อย่างกว้างขวางกับข้อมูลเชิงทัศนะ ไม่ว่าจะเป็น การรู้จำประเภทของวัตถุหลักในภาพ (image classification), การตรวจจับวัตถุในภาพ (object detection), การตรวจจับท่าทาง (pose detection), การรู้จำใบหน้า (face recognition), การแบ่งส่วนภาพตามความหมาย (semantic segmentation), การบรรยายภาพ (scene description, การเพิ่มความละเอียดให้กับภาพ (enhance image resolution, การซ่อม เสริม และกำเนิดภาพ (image reparation/generation), การจำแนกวิดีโอ (video classification), การติดตามวัตถุ (object tracking) เป็นต้น. การประยุกต์ใช้เหล่านี้ อาศัยความคิดสร้างสรรค์และความเข้าใจในภาระกิจ ทฤษฎี กลไกการทำงานของการเรียนรู้ของเครื่อง และในหลาย ๆ ครั้งได้พัฒนาทฤษฎีเฉพาะขึ้นมา. การประยุกต์ใช้ที่น่าสนใจ มีมากมายและยังมีการพัฒนาอย่างต่อเนื่อง บทนี้ เลือกอภิปรายบางส่วนของการประยุกต์ใช้ที่น่าสนใจ เพื่อให้เห็นตัวอย่างของความคิดสร้างสรรค์ในการประยุกต์ใช้โครงข่ายคอนโวลูชั่น.
7.1 การตรวจจับวัตถุในภาพ
การตรวจจับวัตถุในภาพ (object detection) เป็นภาระกิจที่รับอินพุตเป็นภาพ และให้เอาต์พุตเป็นตำแหน่งของวัตถุที่พบในภาพ พร้อมชนิดของวัตถุ. โดยทั่วไป ตำแหน่งของวัตถุ จะระบุด้วยกล่องขอบเขต (bounding box) ซึ่งอาจอ้างอิงถึงด้วยพิกัดแนวนอนและแนวตั้งของจุดศูนย์กลางของกล่องขอบเขต และความกว้างกับความสูงของกล่องขอบเขต.
รูป 1.2 แสดงผลลัพธ์ของการตรวจจับวัตถุในภาพ (ภาพซ้าย) เปรียบเทียบกับการรู้จำประเภทของวัตถุหลักในภาพ (image classification ในภาพขวา). การรู้จำประเภทของวัตถุหลักในภาพ เป็นภาระกิจที่รับอินพุตเป็นภาพ และให้เอาต์พุตเป็นชนิดของวัตถุหลักในภาพ ส่วนการตรวจจับวัตถุในภาพ จะเพิ่มการระบุตำแหน่งของวัตถุออกมาให้ด้วย.
การรู้จำประเภทของวัตถุหลักในภาพ ไม่มีการระบุตำแหน่งของวัตถุภายในภาพ และมักถูกตีกรอบปัญหาเป็นปัญหาการจำแนกประเภท (multi-class classification). แบบจำลองของการรู้จำประเภทของวัตถุหลักในภาพ นิยมใช้โครงข่ายคอนโวลูชั่น ที่โครงสร้างเอาต์พุตใช้ชั้นเชื่อมต่อเต็มที่ตามด้วยฟังก์ชันซอฟต์แมกซ์ ดังเช่น แบบจำลองอเล็กซ์เน็ต ที่ได้อภิปรายในหัวข้อ [sec: AlexNet].
| การรู้จำประเภทของวัตถุหลักในภาพ (image classification) | การตรวจจับวัตถุในภาพ (object detection) |
 |
 |
| output: “Baby Kangaroo” | output: \((x, y, w, h, \mbox{``Baby Kangaroo''})\) |
การตรวจจับวัตถุในภาพ อาจทำได้หลายวิธี. วิธีแบบดั่งเดิม ใช้การจำแนกประเภท ร่วมกับเทคนิคหน้าต่างเลื่อน ดังอภิปรายในหัวข้อ [sec: classic object detection] (หรือเทคนิคอื่นในลักษณะเดียวกัน). หนึ่งในศาสตร์และศิลป์ของการตรวจจับวัตถุในภาพ คือ โยโล่ (YOLO) ซึ่งเป็นระบบตรวจจับวัตถุในภาพแบบเวลาจริง (real-time object detection) และโยโล่ยังมีการทำงานภายใน ที่ใช้โครงสร้างกลไกหลักอย่างเดียว ทำให้การปรับแต่งประสิทธิภาพสามารถทำได้ง่าย.
7.1.0.0.1 โยโล่.
โยโล่ รับอินพุตเป็นภาพสี และให้เอาต์พุตออกมาเป็นกล่องขอบเขตระบุตำแหน่งของวัตถุที่ตรวจจับได้ในภาพ พร้อมชนิดของวัตถุที่พบ. โยโล่ ใช้โครงข่ายคอนโวลูชั่น ในการแปลงจากอินพุตไปเป็นเอาต์พุต. ต่างจากระบบการตรวจจับวัตถุในภาพแบบดั่งเดิม โยโล่ ตั้งปัญหาการตรวจจับวัตถุในภาพ เป็นการหาค่าถดถอย เพื่อทำนายตำแหน่งของวัตถุ และการจำแนกประเภท เพื่อทำนายชนิดของวัตถุที่พบ.
แนวทางคือ เพื่อสามารถตรวจจับตำแหน่งวัตถุได้สูงสุด \(M\) วัตถุต่อภาพ เราต้องการเอาต์พุตเป็นเทนเซอร์ขนาดอย่างน้อย \(5 M\) นั่นคือ สำหรับแต่ละการตรวจจับตำแหน่งวัตถุ โยโล่จะใช้ \(5\) ค่า เพื่อระบุด้วยพิกัดของจุดศูนย์กลางและขนาดของกล่องขอบเขต (\(x, y, w, h\) สำหรับพิกัดแนวนอนและแนวตั้ง ความกว้างและความสูง) พร้อมด้วยค่าความมั่นใจว่าภายในกล่องมีวัตถุอยู่. ค่าความมั่นใจนี้ (confidence ใช้สัญกรณ์ \(C\)) มีเพื่อที่ช่วยให้ผลการทำนายสามารถยืดหยุ่นจำนวนวัตถุในภาพได้ ตั้งแต่ \(0\) วัตถุ (ทุกตำแหน่งตรวจจับ มีค่าความมั่นใจต่ำหมด) ไปจนถึง \(M\) วัตถุ (ทุกตำแหน่งตรวจจับ มีค่าความมั่นใจสูงหมด). อาจมองได้ว่า ค่าความมั่นใจ ทำหน้าที่เป็นเหมือนสวิตช์ปิดเปิดกล่องขอบเขต ว่าจะเลือกผลลัพธ์กล่องไหนบ้างให้ออกไป.
เพื่อให้การฝึกโครงข่ายทำได้อย่างมีประสิทธิิภาพ โยโล่ กำหนดพื้นที่รับผิดชอบของแต่ละตำแหน่งตรวจจับ. การกำหนดพื้นที่รับผิดชอบของตำแหน่งตรวจจับ จำนวน \(M\) ตำแหน่งตรวจจับ เทียบเท่ากับการแบ่งพื้นที่รับผิดชอบของภาพอินพุตออกเป็น \(M\) ส่วน. โยโล่แบ่งพื้นที่ภาพตามแนวนอนและแนวตั้งอย่างละเท่า ๆ กัน และเรียกการแบ่งนี้เป็นเสมือนช่องตาราง หรือ กริด (grid) และเรียกพื้นที่รับผิดชอบแต่ละส่วนว่า กริดเซลล์ (grid cell). รูป 1.3 แสดงแนวคิดนี้ ในรูปแสดงการแบ่งรูปออกเป็น \(7 \times 7\) ส่วน (\(M = 49\)). การกำหนดกริดเซลล์ให้รับผิดชอบพื้นที่อินพุตส่วนไหน ช่วยให้การฝึกทำได้มีประสิทธิภาพมากขึ้น โดยลดความสับสนว่า วัตถุควรจะถูกทายด้วยกริดเซลล์ไหน. มันจะช่วยให้ การกำหนดฟังก์ชันสูญเสีย และการทำเฉลย ทำได้ง่ายขึ้น เพราะถ้าไม่กำหนดความรับผิดชอบให้แน่นอน กริดเซลล์ใด ๆ หนึ่งใน \(M\) กริดเซลล์ อาจทายวัตถุก็ได้ และการคำนวณค่าฟังก์ชันสูญเสียจะยุ่งยากมาก. (ในระหว่างการฝึก ซึ่งการทายอาจจะยังผิดเพี้ยนอยู่มาก มันจะยากที่จะรู้ว่ากริดเซลล์ไหนที่กำลังทายเฉลยวัตถุไหน และยังอาจมีกรณีที่ กริดเซลล์มากกว่าหนึ่งตัว พยายามทายวัตถุเดียวกันอีก.)
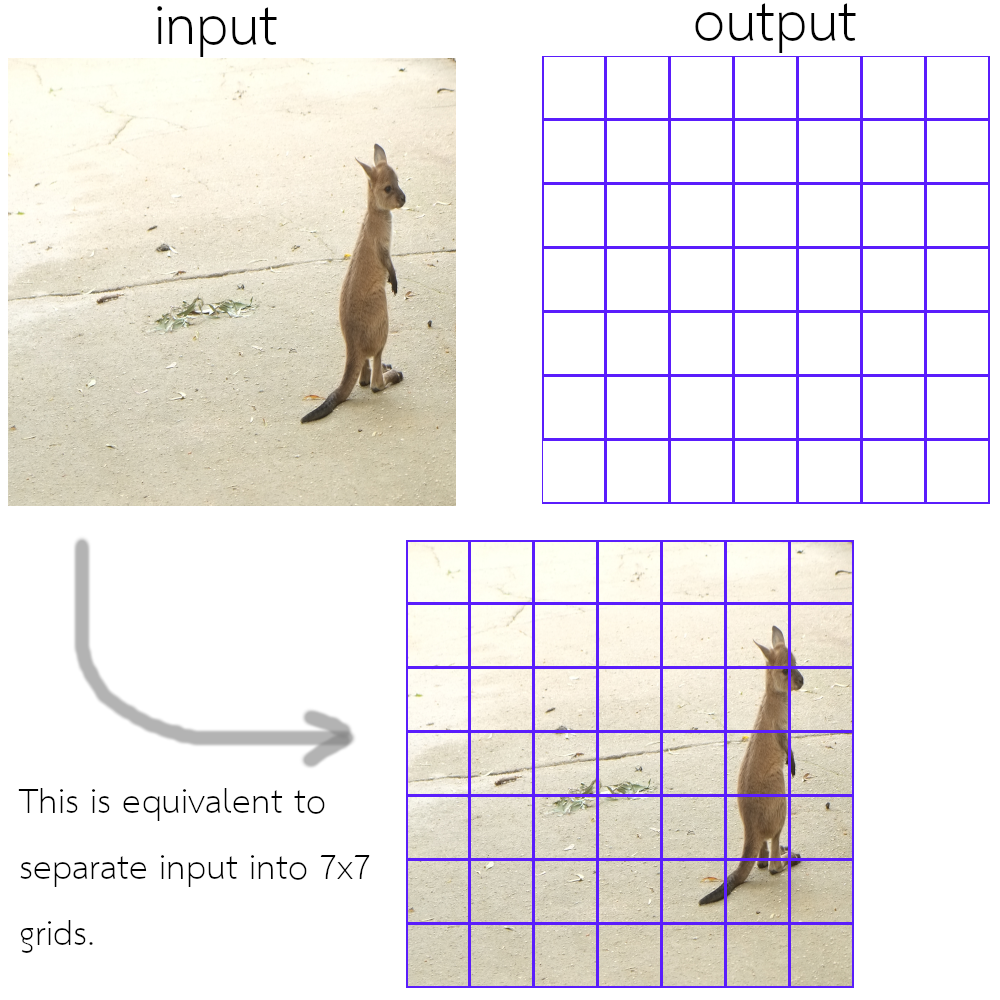
การกำหนดให้แต่ละกริดเซลล์ทายได้เพียงหนึ่งวัตถุ จะจำกัดความสามารถของการตรวจจับภาพวัตถุ โดยเฉพาะกรณีที่วัตถุซ้อนท้บกันและมีจุดศูนย์กลางอยู่ใกล้กัน (ทำให้วัตถุตกอยู่ในความรับผิดชอบของกริดเซลล์เดียวกัน). หลาย ๆ ครั้ง วัตถุที่ซ้อนทับกันนั้น อาจมีขนาดหรือรูปทรงที่แตกต่างกัน ทำให้ แม้จะทับซ้อนกัน ก็สามารถเห็นวัตถุต่าง ๆ ที่ทับซ้อนกันได้อย่างชัดเจน. รูป 1.4 แสดงตัวอย่างกรณีดังกล่าว.
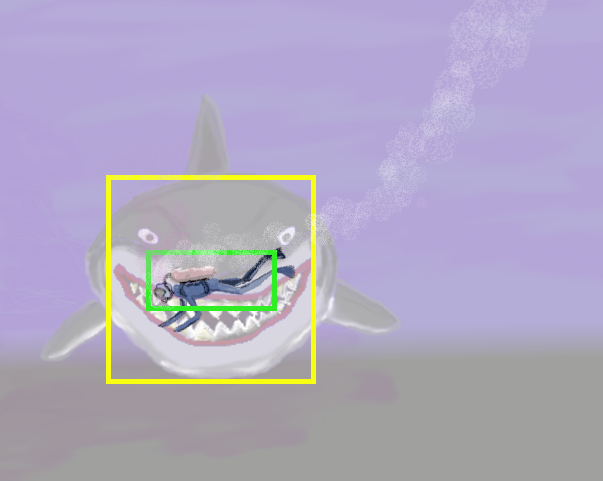
วิธีแก้ไขเบื้องต้นคือ แทนที่จะให้แต่ละกริดเซลล์ทำนายตำแหน่งวัตถุได้แค่หนึ่งอัน ก็แค่อนุญาตให้หนึ่งกริดเซลล์ทำนายตำแหน่งวัตถุได้หลาย ๆ ตำแหน่ง โดยแต่ละการทายก็มีค่าความมั่นใจของตัวเอง. เพียงแต่ ในการฝึก การคำนวณค่าฟังก์ชันสูญเสียจะจัดการให้มีประสิทธิภาพได้อย่างไร. วิธีการที่ออกแบบมาเพื่อบรรเทาประเด็นนี้ คือ เทคนิคกล่องสมอ (anchor box).
7.1.0.0.2 เทคนิคกล่องสมอ.
การทายตำแหน่งแต่ละกล่อง ในกริดเซลล์ จะเรียกว่า กล่องสมอ โดยหนึ่งกริดเซลล์ สามารถทำนายกล่องสมอได้ \(B\) กล่อง และ กล่องสมอแต่ละกล่อง จะถูกกำหนดค่าเริ่มต้นให้มีขนาดหรือสัดส่วนต่างกัน. การฝึก จะใช้ค่าไอโอยูระหว่างกล่องสมอกับเฉลย เป็นดัชนีกำหนดว่า กล่องสมอใดจะรับผิดชอบเฉลยวัตถุใด (และอาจมีกฎในการกำหนดความรับผิดชอบในกรณีที่ค่าไอโอยูบังเอิญเท่ากัน). รูป 1.5 แสดงการใช้งานเทคนิคกล่องสมอในโยโล่.
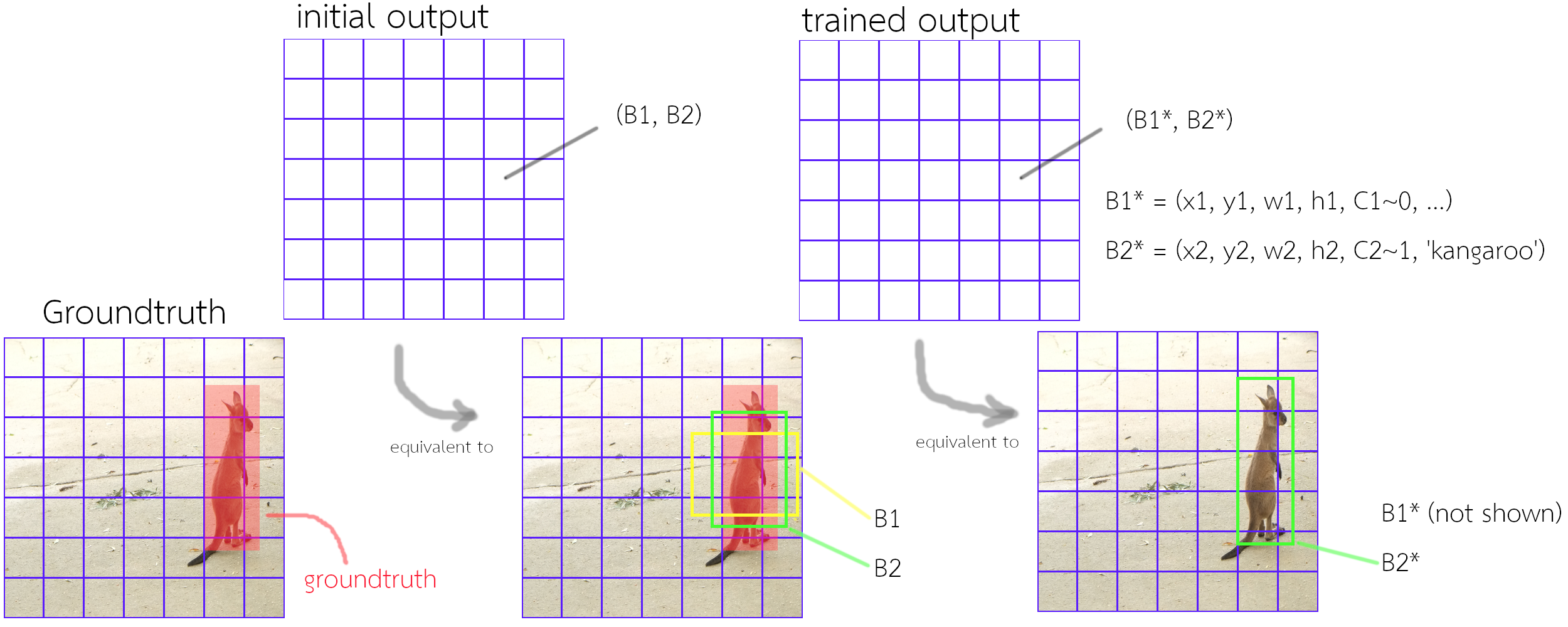
สำหรับการตรวจจับวัตถุในภาพได้ครอบคลุม \(K\) ชนิดวัตถุ แต่ละกล่องสมอจะมี \(5 + K\) ค่า สำหรับตำแหน่งและขนาดของกล่องขอบเขต (\(x, y, w, h\)), ค่าความมั่นใจว่ามีวัตถุอยู่ภายในกล่อง \(C\), และค่าความน่าจะเป็นของวัตถุแต่ละชนิด \(p(1), \ldots, p(K)\). ดังนั้น สำหรับ \(M\) กริดเซลล์ และ \(B\) กล่องสมอต่อกริดเซลล์ แล้ว เอาต์พุตของโยโล่ \(\boldsymbol{Y} \in \mathbb{R}^{M \cdot B \cdot (5 + K)}\) หรือ \(\boldsymbol{Y} = [\tilde{x}_{mb}, \tilde{y}_{mb}, \tilde{w}_{mb}, \tilde{h}_{mb}\) \(, \hat{C}_{mb},\) \(\hat{p}_{mb}(1), \ldots, \hat{p}_{mb}(K)]\) สำหรับ \(m = 1, \ldots, M; b = 1, \ldots, B\).
เพื่อให้การฝึกแบบจำลองทำได้มีประสิทธิภาพมากขึ้น แทนที่จะให้แบบจำลองทำนายค่าพิกัดและขนาดของกล่องขอบเขตโดยตรง ค่าที่แบบจำลองทำนาย \(\tilde{x}_{mb}, \tilde{y}_{mb}, \tilde{w}_{mb}, \tilde{h}_{mb}\) จะถูกคำนวณไปเป็นค่าพิกัดและขนาดของกล่องขอบเขต ดังนี้ (ละตัวห้อยออก เพื่อความกระชับ) \[\begin{eqnarray} \hat{x} &=& c_w \cdot \sigma(\tilde{x}) + c_x \label{eq: YOLO x} \\ \hat{y} &=& c_h \cdot \sigma(\tilde{y}) + c_y \label{eq: YOLO y} \\ \hat{w} &=& p_w \cdot \exp(\tilde{w}) \label{eq: YOLO w} \\ \hat{h} &=& p_h \cdot \exp(\tilde{h}) \label{eq: YOLO h} \end{eqnarray}\] เมื่อ \(\hat{x}\) กับ \(\hat{y}\) เป็นพิกัดแนวนอนกับแนวตั้งของศูนย์กลางกล่องขอบเขตที่ทำนาย และ \(\hat{w}\) กับ \(\hat{h}\) เป็นความกว้างกับความสูงของกล่องขอบเขตที่ทำนาย โดย \(\sigma(\cdot)\) คือฟังก์ชันซิกมอยด์ (มีค่าระหว่างศูนย์ถึงหนึ่ง), \(c_x\) กับ \(c_y\) เป็นพิกัดมุมซ้ายบนของกริดเซลล์, \(c_w\) กับ \(c_h\) เป็นความกว้างกับความสูงของกริดเซลล์, และ \(p_w\) กับ \(p_h\) เป็นค่าฐานของความกว้างกับความสูงของกล่องสมอ.
สังเกตว่า ถ้า \(\tilde{x}\) มีค่าบวกขนาดใหญ่มาก จะทำให้ \(\hat{x}\) อยู่ขอบขวาของกริดเซลล์. ถ้า \(\tilde{x}\) มีค่าลบขนาดใหญ่มาก จะทำให้ \(\hat{x}\) อยู่ขอบซ้ายของกริดเซลล์. ถ้า \(\tilde{x}\) มีค่าเป็นศูนย์ จะทำให้ \(\hat{x}\) อยู่ตรงกลางของกริดเซลล์. ความสัมพันธ์ระหว่างค่า \(\tilde{y}\) กับ \(\hat{y}\) ก็เป็นในทำนองเดียวกัน. ส่วนถ้า \(\tilde{w}\) มีค่าบวก จะทำให้ \(\hat{w}\) กว้างกว่าค่าฐาน \(p_w\). ถ้า \(\tilde{w}\) มีค่าลบ จะทำให้ \(\hat{w}\) แคบกว่าค่าฐาน \(p_w\). ถ้า \(\tilde{w}\) มีค่าศูนย์ จะทำให้ \(\hat{w}\) กว้างเท่ากับค่าฐาน \(p_w\). ความสัมพันธ์ระหว่างค่า \(\tilde{h}\) กับ \(\hat{h}\) ก็เป็นในทำนองเดียวกัน.
ค่าฐานของแต่ละกล่องสมอ \(p_w\) และ \(p_h\) อาจเลือกกำหนดเองตามเห็นว่าเหมาะสม. คณะของเรดมอน ใช้การจัดกลุ่มข้อมูลด้วยวิธีเค-มีนส์ (K-means) สำรวจกล่องขอบเขตเฉลยของข้อมูลฝึกหัด แล้วใช้ค่า ต่าง ๆ (centroids) ที่ได้มา เป็นค่าฐานของกล่องสมอต่าง ๆ.
โยโล่ นิยาม ค่าความมั่นใจ \(\hat{C} = \mathrm{Pr}(\mbox{Object}) \cdot \mathrm{IOU}\) เมื่อ \(\mathrm{Pr}(\mbox{Object})\) แทนค่าความน่าจะเป็นที่กล่องขอบเขตจะมีวัตถุ และ \(\mathrm{IOU}\) แทนค่าไอโอยูระหว่างกล่องขอบเขตที่ทายกับกล่องขอบเขตเฉลย. ดังนั้นค่าความมั่นใจเฉลย \(C = 0\) ถ้าไม่มีวัตถุอยู่ภายในกริดเซลล์ และ \(C = \mathrm{IOU}\) ถ้ามีวัตถุอยู่ภายในกริดเซลล์.
ในการฝึกการตรวจจับวัตถุในภาพ โยโล่กำหนดฟังก์ชันสูญเสียดังนี้ \[\begin{eqnarray} \mathrm{loss} &=& \lambda_{\mathrm{coord}} \sum_{m=1}^M \sum_{b=1}^B \boldsymbol{1}_{mb}^{\mathrm{obj}} \cdot \left( (\hat{x}_{mb} - x_{mb})^2 + (\hat{y}_{mb} - y_{mb})^2 \right) \nonumber \\ &\;& + \lambda_{\mathrm{coord}} \sum_{m=1}^M \sum_{b=1}^B \boldsymbol{1}_{mb}^{\mathrm{obj}} \cdot \left( (\sqrt{\hat{w}_{mb}} - \sqrt{w_{mb}})^2 + (\sqrt{\hat{h}_{mb}} - \sqrt{h_{mb}})^2 \right) \nonumber \\ &\;& + \sum_{m=1}^M \sum_{b=1}^B \boldsymbol{1}_{mb}^{\mathrm{obj}} \cdot \left( \hat{C}_{mb} - C_{mb} \right)^2 + \lambda_{\mathrm{noobj}} \sum_{m=1}^M \sum_{b=1}^B \boldsymbol{1}_{mb}^{\mathrm{noobj}} \cdot \left( \hat{C}_{mb} - C_{mb} \right)^2 \nonumber \\ &\;& + \sum_{m=1}^M \sum_{b=1}^B \boldsymbol{1}_{mb}^{\mathrm{obj}} \cdot \sum_{k \in \mathrm{classes}} \cdot \left( \hat{p}_{mb}(k) - p_{mb}(k) \right)^2 \label{eq: YOLO loss function} \end{eqnarray}\] เมื่อ \(p_{mb}(k)\) คือเฉลยชนิดวัตถุที่กริดเซลล์ \(m\) กล่องสมอ \(b\) โดย \(p_{mb}(k) = 1\) ถ้าที่กล่องสมอ มีภาพวัตถุชนิด \(k\) และ \(p_{mb}(k) = 0\) ถ้าที่กล่องสมอ มีภาพวัตถุชนิดอื่น. สัญกรณ์ \(\boldsymbol{1}_{mb}^{\mathrm{obj}}\) ใช้ระบุว่ากล่องสมอ \(b\) ในกริดเซลล์ \(m\) รับผิดชอบการทาย นั่นคือ \(\boldsymbol{1}_{mb}^{\mathrm{obj}} = 1\) เมื่อ กล่องสมอ \(b\) ในกริดเซลล์ \(m\) มีเฉลยที่รับผิดชอบอยู่ ถ้าไม่อย่างนั้นให้ \(\boldsymbol{1}_{mb}^{\mathrm{obj}} = 0\). โยโล่กำหนดการรับผิดชอบของกล่องสมอ โดยให้กล่องสมอที่มีค่าไอโอยูร่วมกับกรอบตัวอย่างเฉลยมากที่สุด ทำหน้าที่รับผิดชอบการทายเฉลยนั้น. สัญกรณ์ \(\boldsymbol{1}_{mb}^{\mathrm{noobj}}\) ใช้ระบุว่ากล่องสมอ \(b\) ในกริดเซลล์ \(m\) ไม่มีวัตถุอยู่ ซึ่ง \(\boldsymbol{1}_{mb}^{\mathrm{noobj}} = 1 - \boldsymbol{1}_{mb}^{\mathrm{obj}}\).
เนื่องจาก คณะของเรดมอน พบว่า ภาพต่าง ๆ ที่ใช้ฝึก ส่วนใหญ่มีวัตถุอยู่ไม่มาก. กล่องสมอส่วนใหญ่ไม่มีวัตถุ และสัดส่วนการไม่มีวัตถุต่อการมีวัตถุสูงมาก (ข้อมูลไม่สมดุลย์ unbalanced data. แบบฝึกหัด [ex: binding affinity]). ดังนั้น คณะของเรดมอน เลือกใช้แนวทางหนึ่งที่นิยมใช้บรรเทาปัญหาเช่นนี้ คือใช้ค่าน้ำหนักที่ต่างกันเพื่อชดเชย. ค่า \(\lambda_{\mathrm{coord}}\) และ \(\lambda_{\mathrm{noobj}}\) เป็นเพียงเทคนิคเชิงเลข เพื่อชดเชยความไม่สมดุลย์ของข้อมูล (ซึ่งคณะของเรดมอน เลือกใช้ \(\lambda_{\mathrm{coord}} = 5\) และ \(\lambda_{\mathrm{noobj}} = 0.5\)).
สังเกตว่า การคำนวณค่าผิดพลาดของความกว้างและความสูง ทำผ่านค่ารากที่สอง. เนื่องจาก ค่าผิดพลาดสัมบูรณ์ ของการทำนายขนาดสำหรับกล่องขอบเขตขนาดเล็ก แม้ตัวเลขจะเท่ากับค่าผิดพลาดสัมบูรณ์ ของการทำนายขนาดสำหรับกล่องขอบเขตขนาดใหญ่ แต่ถือเป็นความผิดพลาดที่รุนแรงกว่า. ตัวอย่างเช่น การทายความกว้างผิดไป \(10\) สำหรับความกว้าง \(500\) นั้นถือว่าเล็กน้อยมาก จนผู้ใช้อาจไม่ได้เห็นความแตกต่าง แต่ การทายความกว้างผิดไป \(10\) สำหรับความกว้าง \(5\) นั้นถือว่าผิดพลาดรุนแรงมาก และผลลัพธ์ก็เห็นได้อย่างชัดแจ้ง. คณะของเรดมอน ใช้เทคนิคเชิงเลข โดยคำนวณความแตกต่างของค่ารากที่สองแทน เพื่อช่วยบรรเทาปัญหานี้.
ในกระบวนการฝึก คณะของเรดมอน ใช้การฝึกก่อน โดยฝึกแบบจำลองกับงานจำแนกชนิดวัตถุหลักในภาพก่อนจนแบบจำลองทำงานได้ดีแล้ว. จากนั้นจึงเพิ่มชั้นคำนวณท้าย ๆ (ด้านเอาต์พุต) เข้าไปแล้วจึงฝึกแบบจำลองสำหรับภาระกิจการตรวจจับวัตถุในภาพ.
หลังจากฝึกเสร็จ ในการงานอนุมาน ค่าเอาต์พุตจะถูกนำมาประมวลผล โดยค่าของกล่องสมอที่ \(\hat{C} > \tau\) จะถูกนำมาคำนวณตำแหน่งและขนาดของกล่องขอบเขต (สมการ \(\eqref{eq: YOLO x}\), \(\eqref{eq: YOLO y}\), \(\eqref{eq: YOLO w}\), \(\eqref{eq: YOLO h}\)) และวัตถุจะถูกอนุมานเป็นชนิด \(k^\ast = \arg\max_k \hat{p}(k)\) เมื่อ \(\tau\) เป็นระดับค่าขีดแบ่งที่กำหนด.
7.2 การซ่อม เสริม และก่อกำเนิดภาพ
การซ่อมภาพ คือการเติมส่วนของภาพที่ต้องการ (ส่วนของภาพที่เสียหาย) โดยคำนึงถึงบริเวณรอบข้าง และลักษณะของภาพโดยรวม. การเสริมภาพ มีความหมายครอบคลุมการเพิ่มความละเอียดให้กับภาพ (หัวข้อ 1.2.1). การก่อกำเนิดภาพ คือการสร้างภาพขึ้นมาใหม่ทั้งภาพ โดยภาพที่สร้างขึ้นเป็นภาพในลักษณะที่ต้องการ เช่น ดูคล้ายภาพจริง (หัวข้อ 1.2.2).
การซ่อม เสริม และก่อกำเนิดภาพ เป็นศาสตร์ที่กำลังได้รับความสนใจและมีการพัฒนาอย่างรวดเร็ว มีหลายแนวทาง เช่น พิกเซลอาร์เอนเอน (PixelRNN), ตัวเข้ารหัสอัตแบบเปลี่ยนแปลง (Variational Autoencoder), หรือโครงข่ายปรปักษ์เชิงสร้าง (Generative Adversarial Network).
ความท้าทายที่สำคัญสำหรับภาระกิจเช่นนี้ โดยเฉพาะการก่อกำเนิดภาพ คือ ตัวภาระกิจเป็นเสมือนการเรียนรู้ความน่าจะเป็นของภาพ (ไม่ว่าจะเรียนรู้ชัดแจ้งโดยตรง ซึ่งได้ค่าฟังก์ชันความหนาแน่นความน่าจะเป็นออกมา หรือโดยนัย ซึ่งคือทำภาระกิจได้ แต่ไม่ได้ค่าฟังก์ชันความหนาแน่นความน่าจะเป็น). จากมุมของปริภูมิมิติ ภาพเป็นจุดข้อมูลที่อยู่ในปริภูมิหลายมิติ ที่มีจำนวนมิติมหาศาล 1. นั่นคือ ภาพสีขนาด \(W \times H\) (สัญกรณ์ \(\boldsymbol{X} \in \mathbb{R}^{3 \times W \times H}\)) แต่ละภาพเปรียบเสมือนจุดหนึ่งจุดในปริภูมิ \(3 \cdot W \cdot H\) มิติ. การประมาณฟังก์ชันความหนาแน่นความน่าจะเป็น \(p(\boldsymbol{X})\) ทำได้ยากมาก และต้องการข้อมูลจำนวนมหาศาล.
โครงข่ายปรปักษ์เชิงสร้าง จัดเป็นศาสตร์และศิลป์ที่สำคัญของการเรียนรู้ของเครื่อง ดังอภิปรายเกริ่นในบทที่ [chapter: Deep Learning] และ ได้แสดงให้เห็นว่า โครงข่ายปรปักษ์เชิงสร้างเป็นแนวทางที่ช่วยแก้ปัญหาของภารกิจการก่อกำเนิดภาพได้. หัวข้อ 1.2.2 อภิปรายโครงข่ายปรปักษ์เชิงสร้าง รวมถึงอุปสรรคความท้าทายในการประยุกต์ใช้โครงข่ายปรปักษ์เชิงสร้าง และแนวทางในการบรรเทาอุปสรรค.
7.2.1 การเพิ่มความละเอียดให้กับภาพ
การเพิ่มความละเอียดให้กับภาพ คือ กระบวนการที่รับภาพความละเอียดต่ำ (low-resolution image) และประมาณภาพความละเอียดสูง (high-resolution) ออกมา.
การเพิ่มความละเอียดให้กับภาพ อาจทำได้หลายวิธี. คณะของตง ทำการอัพแซมปลิ้ง (upsampling) ซึ่งคือการเพิ่มพิกเซลเข้าไปในภาพ โดยค่าพิกเซลที่เพิ่มขึ้นจะได้จากการทำการประมาณค่าในช่วงแบบไบคิวบิก (bicubic interpolation). จากนั้นใช้โครงข่ายคอนโวลูชั่นในการประมาณภาพความละเอียดสูงออกมา (เพื่อปรับปรุงคุณภาพจากการประมาณค่าในช่วงแบบไบคิวบิก).
กล่าวคือ จากภาพความละเอียดต่ำ \(\boldsymbol{\tilde{X}}\) คณะของตงสร้างภาพความละเอียดสูง \(\boldsymbol{X}'\) ขึ้นด้วยวิธีการประมาณค่าในช่วงแบบไบคิวบิก แล้วใช้ \(\boldsymbol{X}'\) เป็นอินพุตของโครงข่ายคอนโวลูชั่น เพื่อทำนาย \(\boldsymbol{\hat{X}}\) (ซึ่ง แม้จะความละเอียดเท่ากัน แต่ \(\boldsymbol{\hat{X}}\) มีคุณภาพดีกว่า \(\boldsymbol{X}'\)). หาก \(f\) คือฟังก์ชันที่แทนการคำนวณของโครงข่าย และ \(\boldsymbol{\Theta}\) เป็นค่าพารามิเตอร์ต่าง ๆ ของโครงข่าย โครงข่ายคอนโวลูชั่นถูกฝึกให้ทำนาย \(\boldsymbol{\hat{X}} = f(\boldsymbol{X}'; \boldsymbol{\Theta})\) ให้ใกล้เคียงกับเฉลย (ที่เป็นภาพความละเอียดสูง) \(\boldsymbol{X}\) ให้มากที่สุด. นั่นคือ ฟังก์ชันสูญเสีย \(\mathrm{loss}(\boldsymbol{\Theta}) = \frac{1}{N} \sum_{n=1}^N \| f(\boldsymbol{X}'_n; \boldsymbol{\Theta}) - \boldsymbol{X}_n \|^2\) เมื่อ \(N\) คือจำนวนข้อมูลฝึกทั้งหมด.
คุณภาพของการเพิ่มความละเอียดให้กับภาพ อาจประเมินจาก ค่าผิดพลาดกำลังสองเฉลี่ย เช่นเดียวกับภาระกิจการหาค่าถดถอยทั่วไป เช่น \(\mathrm{mse} = \frac{1}{W \cdot H} \sum_i \sum_j (\hat{x}_{i,j} - x_{i,j})^2\) เมื่อ \(W\) กับ \(H\) เป็นความกว้างกับสูงของภาพ และ \(\hat{x}_{i,j}\) เป็นค่าพิกเซลของภาพที่เพิ่มความละเอียดขึ้นจากภาพความละเอียดต่ำ \(\tilde{\boldsymbol{X}}\). โดย ภาพความละเอียดต่ำ \(\tilde{\boldsymbol{X}}\) เป็นภาพที่ถูกลดความละเอียดลงจากภาพความละเอียดสูง \(\boldsymbol{X}\). ภาพความละเอียดสูง \(\boldsymbol{X}\) มีค่าพิกเซลต่าง ๆ เป็น \(x_{i,j}\) และ \(i\) กับ \(j\) คือ ดัชนีแนวนอนกับแนวตั้งของภาพ. อย่างไรก็ดี แม้ค่าผิดพลาดกำลังสองเฉลี่ยพอใช้งานได้ แต่นักวิจัยต่างพบว่า ค่าผิดพลาดกำลังสองเฉลี่ยไม่สัมพันธ์กับคุณภาพของภาพที่คนรับรู้. คุณภาพของภาพจึงมักวัดด้วยดัชนีอื่น ๆ ได้แก่ อัตราส่วนสัญญาณสูงสุดต่อสัญญาณรบกวน (peak signal-to-noise ration คำย่อ PSNR), ความคล้ายคลึงเชิงโครงสร้าง (structural similarity คำย่อ SSIM), เงื่อนไขความเที่ยงตรง (fidelity criterion คำย่อ IFC), มาตราวัดคุณภาพสัญญาณรบกวน (noise quality measure คำย่อ NQM), อัตราส่วนสัญญาณสูงสุดปรับค่าน้ำหนักต่อสัญญาณรบกวน (weighted peak signal-to-noise ratio คำย่อ WPSNR), หรือ ดัชนีความคล้ายคลึงเชิงโครงสร้างหลายสเกล (multi-scale structure similarity index คำย่อ MSSSIM) เป็นต้น.
ต่างจากงานของตงและคณะ คณะของชือ ใช้โครงข่ายคอนโวลูชั่น เพื่อเพิ่มความละเอียดให้กับภาพ โดยรับอินพุตเป็นภาพความละเอียดต่ำโดยตรง และให้เอาต์พุตสุดท้ายออกมาเป็นภาพความละเอียดสูงได้เลย. การใช้โครงข่ายคอนโวลูชั่นกับภาพความละเอียดต่ำโดยตรง ช่วยลดภาระการคำนวณลงไปได้มาก และคณะของชือ ยังแสดงให้เห็นคุณภาพของผลลัพธ์ที่ดีขึ้นด้วย.
กลไกสำคัญที่ชือและคณะใช้ อยู่ที่ชั้นคำนวณท้ายสุด. สำหรับภาพขนาด \(W \times H\) (ช่องสีเดียว 2 ) และต้องการขยายความละเอียดขึ้น \(r\) เท่า (นั่นคือ ภาพจะถูกขยายเป็น ภาพผลลัพธ์ขนาด \(r W \times r H\)) คณะของชือ ออกแบบโครงข่ายคอนโวลูชั่นที่ให้เอาต์พุตออกมา เป็นแผนที่ลักษณะสำคัญขนาดเท่ากับขนาดภาพอินพุต แต่มีจำนวนแผนที่เท่ากับ \(r^2\). แล้วภาพผลลัพธ์ จะสร้างขึ้นจากการจัดเรียงแผนที่ลักษณะสำคัญขนาด \(W \times H\) จำนวน \(r^2\) แผ่นที่ ให้เป็นแผนที่เดียว ขนาด \(r W \times r H\) ซึ่งคือภาพความละเอียดสูงที่ต้องการ. กลไกของการจัดเรียงผลลัพธ์แผนที่สำคัญเช่นนี้ เรียกว่า กลไกพิกเซลย่อย ซึ่งเป็นรูปหนึ่งของชั้นดีคอนโวลูชั่น (deconvolution layer). ชั้นดีคอนโวลูชั่น อาจทำได้หลายรูปแบบ ชือและคณะ แจกแจงและอภิปรายข้อแตกต่างของชั้นดีคอนโวลูชั่นแบบต่าง ๆ. รูป 1.6 แสดงจุดเด่น (รับอินพุตเป็นภาพความละเอียดต่ำ และให้เอาต์พุตเป็นภาพความละเอียดสูงได้โดยตรง) และกลไกสำคัญ (ชั้นดีคอนโวลูชั่น ที่จัดเรียงแผนที่ลักษณะสำคัญ \(r^2\) แผนที่ เป็นผลลัพธ์ ภาพเดียวที่เป็นมีความละเอียดเพิ่มเป็น \(r\) เท่า).

7.2.2 โครงข่ายปรปักษ์เชิงสร้าง
โครงข่ายปรปักษ์เชิงสร้าง 3 (Generative Adversarial Networks คำย่อ GANs) หมายถึง โครงข่ายประสาทเทียมที่สามารถเรียนรู้ความน่าจะเป็นของข้อมูลที่มีจำนวนมิิติสูง ๆ และมีหลาย ๆ โหมดได้ (high-dimensional and multi-modal distribution) โดยโครงข่ายถูกเตรียมด้วยวิธีการฝึกแบบปรปักษ์. ด้วยกลไกวิธีการฝึกแบบปรปักษ์ ที่ใช้การเรียนรู้แบบกึ่งมีผู้ช่วยสอนและการเรียนรู้แบบไม่มีผู้สอน โครงข่ายปรปักษ์เชิงสร้างสามารถใช้ประโยชน์จากข้อมูลจำนวนมากที่ไม่มีฉลากเฉลยได้ ซึ่งข้อมูลจำนวนมากนั้น จำเป็นต่อการเรียนรู้ความน่าจะเป็นของข้อมูลที่มีจำนวนมิิติสูง ๆ (เช่น ข้อมูลรูปภาพ).
อย่างไรก็ตาม การเรียนรู้ความน่าจะเป็นของข้อมูลด้วยโครงข่ายปรปักษ์เชิงสร้าง อาจเป็นเพียงการเรียนรู้เชิงนัย นั่นคือ อาจไม่ได้ค่าความน่าจะเป็นหรือไม่ได้ฟังก์ชันความหนาแน่นความน่าจะเป็น. นั่นคือ โครงข่ายอาจสามารถสังเคราะห์ หรือสร้างตัวอย่างข้อมูลขึ้นมาใหม่ได้ โดยตัวอย่างข้อมูลที่สร้างขึ้นมาใหม่ มีลักษณะในแบบเดียวกับตัวอย่างข้อมูลจริง (กล่าวคือ มีความเป็นไปได้สูงว่ามาจากการแจกแจงเดียวกัน). หากข้อมูลที่กล่าวถึง คือภาพ โครงข่ายปรปักษ์เชิงสร้าง อาจสามารถสร้างตัวอย่างภาพขึ้นมาใหม่ ซึ่งภาพที่สร้างขึ้นนี้อาจดูเหมือนภาพถ่ายจริง ซึ่งเบื้องหลังหมายถึงว่า โครงข่ายได้เรียนรู้การแจกแจงข้อมูลของภาพถ่ายจริง และสามารถสังเคราะห์ตัวอย่างข้อมูลจากการแจกแจงนั้นได้ แต่ฟังก์ชันการแจกแจงนั้น อาจไม่สามารถเข้าถึงได้โดยตรง.
วิธีการฝึกแบบปรปักษ์ (adversarial training) มีลักษณะเด่น คือ การใช้โครงข่ายสองโครงข่ายในการฝึก และโครงข่ายทั้งสองถูกฝึกโดยมีเป้าหมายที่ขัดแย้งกัน. คณะของกูดเฟโล เสนอโครงข่ายปรปักษ์เชิงสร้าง เพื่อสร้างตัวอย่างภาพต่าง ๆ ที่เหมือนภาพถ่ายจริงออกมา. วิธีการฝึกแบบปรปักษ์ ใช้โครงข่ายสองโครงข่าย หนึ่งเรียกว่า โครงข่ายแบ่งแยก (discriminator ใช้สัญกรณ์ \(\mathcal{D}\)) และอีกหนึ่ง เรียกว่า โครงข่ายก่อกำเนิด (generator ใช้สัญกรณ์ \(\mathcal{G}\)). โครงข่ายแบ่งแยก \(\mathcal{D}\) รับอินพุตเป็นภาพ และทำหน้าที่ทำนายว่า ภาพที่รับเข้ามาเป็นภาพถ่ายจริง หรือว่าเป็นภาพปลอม (ภาพที่สร้างขึ้น). โครงข่ายก่อกำเนิด \(\mathcal{G}\) รับอินพุตเป็นค่าสุ่ม 4 และทำหน้าที่สร้างภาพขึ้นมา. ในกระบวนการฝึก โครงข่ายแบ่งแยก \(\mathcal{D}\) ถูกฝึก โดยมีเป้าหมายคือ การแแยกแยะให้ถูกต้องมากที่สุด ในขณะที่โครงข่ายก่อกำเนิด \(\mathcal{G}\) ถูกฝึก โดยมีเป้าหมายคือ การสร้างภาพปลอมให้เหมือน จนโครงข่ายแบ่งแยก \(\mathcal{D}\) ทายถูกน้อยที่สุด.
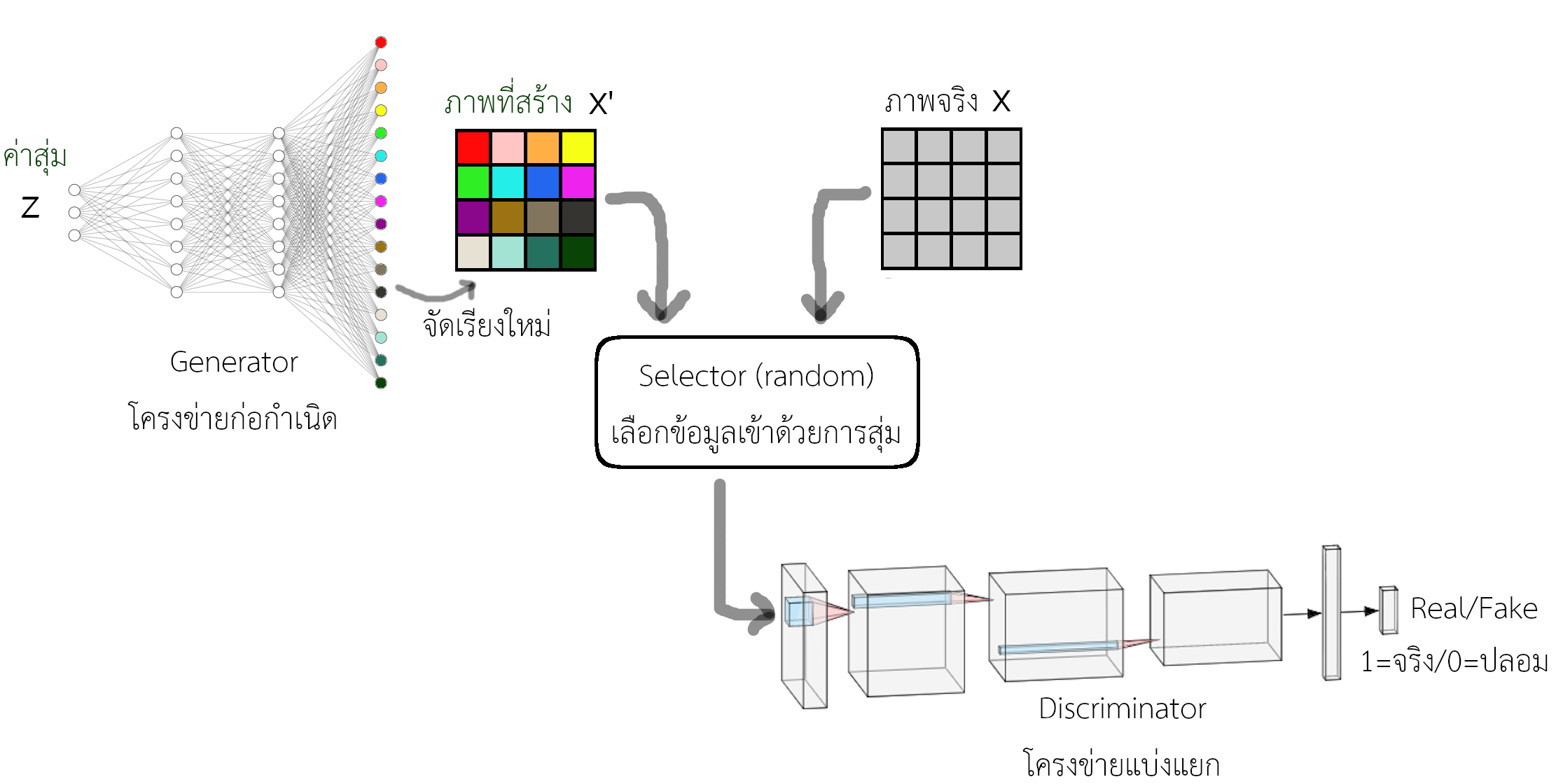
รูป 1.7 แสดงแนวคิดของวิธีการฝึกแบบปรปักษ์ ซึ่งเป็นกลไกหลักของโครงสร้างปรปักษ์เชิงสร้าง. ในการฝึก โครงข่ายแบ่งแยก \(\mathcal{D}\) จะรับอินพุต เป็นภาพ ที่ถูกสุ่มขึ้นมา โดยภาพที่ได้อาจสุ่มจากภาพจริง หรืออาจสุ่มมาจากภาพปลอมที่สร้างโดย โครงข่ายก่อกำเนิด \(\mathcal{G}\) แล้วให้ โครงข่ายแบ่งแยก \(\mathcal{D}\) ทำนาย. ผลของการทำนายผิดหรือถูก จะถูกนำไปปรับค่าน้ำหนักเพื่อให้ โครงข่ายแบ่งแยก \(\mathcal{D}\) ทำงานได้ดีขึ้น แบ่งแยกได้ดีขึ้น (ทายถูกมากขึ้น) และก็จะถูกนำไปปรับค่าน้ำหนัก โครงข่ายก่อกำเนิด \(\mathcal{G}\) เพื่อให้ \(\mathcal{G}\) สร้างภาพได้ดีขึ้น (หลอก \(\mathcal{D}\) ได้ดีขึ้น ทำให้ \(\mathcal{D}\) ทายถูกน้อยลง). หากโครงข่ายก่อกำเนิด \(\mathcal{G}\) สามารถหลอกโครงข่ายแบ่งแยก \(\mathcal{D}\) ได้โดยสมบูรณ์แล้ว โครงข่ายแบ่งแยก \(\mathcal{D}\) จะทายถูกได้ประมาณครึ่ง ๆ. นั่นคือ ถ้าภาพที่สร้างขึ้นเหมือนภาพจริง โอกาสคืิอเท่ากับเดาสุ่ม ซึ่งถ้าเดาดี ๆ โอกาสถูกคือแค่ประมาณ \(0.5\) (หรือ \(50\%\)). หมายเหตุ รูป 1.7 อาจแสดงโครงข่ายก่อกำเนิดด้วยโครงข่ายเชื่อมต่อเต็มที่ แต่การเปลี่ยนโครงสร้างไปเป็นโครงข่ายคอนโวลูชั่นก็สามารถทำได้ (ดู เพิ่มเติม).
การฝึกโครงข่ายปรปักษ์เชิงสร้าง กล่าวโดยเจาะจงแล้วก็คือการแก้ปัญหาค่าดีที่สุด ในนิพจน์ \(\eqref{eq: convapp GAN opt prob}\) ได้แก่ \[\begin{eqnarray} \min_{\mathcal{G}} \max_{\mathcal{D}} V(\mathcal{G}, \mathcal{D}) \label{eq: convapp GAN opt prob} \end{eqnarray}\] เมื่อ \[\begin{eqnarray} V(\mathcal{G}, \mathcal{D}) &=& E_{\boldsymbol{X} \sim p_{data}}[\log \mathcal{D}(\boldsymbol{X})] + E_{\boldsymbol{X} \sim p_{\mathcal{G}}}[\log(1 - \mathcal{D}(\boldsymbol{X}))] \label{eq: convapp GAN obj function} \end{eqnarray}\] โดย \(\mathcal{D}(\boldsymbol{X}) \in (0,1)\) และ \(\mathcal{D}(\boldsymbol{X}) \approx 1\) หมายถึง โครงข่ายแบ่งแยกทายว่า \(\boldsymbol{X}\) เป็นภาพจริง และ \(\mathcal{D}(\boldsymbol{X}) \approx 0\) หมายถึง โครงข่ายแบ่งแยกทายว่า \(\boldsymbol{X}\) เป็นภาพปลอมที่สร้างขึ้น.
พจน์ \(E_{\boldsymbol{X} \sim p_{data}}[\log \mathcal{D}(\boldsymbol{X})]\) หมายถึง ค่าคาดหมายของลอการิทึ่มของผลลัพธ์จากโครงข่ายแบ่งแยก เมื่ออินพุตของโครงข่ายแบ่งแยกมีการแจกแจงตามข้อมูลจริง (ดังระบุด้วยสัญกรณ์ \(\boldsymbol{X} \sim p_{data}\)) หรือกล่าวง่าย ๆ คือ เมื่ออินพุตเป็นภาพจริง. หากโครงข่ายแบ่งแยกทำงานถูกต้องโดยสมบูรณ์ แล้ว \(\mathcal{D}(\boldsymbol{X}) \approx 1\) สำหรับทุก ๆ ภาพจริง และ พจน์ \(E_{\boldsymbol{X} \sim p_{data}}[\log \mathcal{D}(\boldsymbol{X})] \approx 0\).
ส่วนพจน์ 5 \(E_{\boldsymbol{X} \sim p_{\mathcal{G}}}[\log(1 - \mathcal{D}(\boldsymbol{X}))]\) แสดงค่าคาดหมายของลอการิทึ่มของ \(1 - \mathcal{D}(\boldsymbol{X})\) เมื่ออินพุตของมีการแจกแจงตามการแจกแจงจากโครงข่ายก่อกำเนิด (ดังระบุด้วยสัญกรณ์ \(\boldsymbol{X} \sim p_{\mathcal{G}}\)) หรือกล่าวง่าย ๆ คือ เมื่ออินพุตถูกสร้างขึ้นจากโครงข่ายก่อกำเนิด. หากโครงข่ายแบ่งแยกทำงานถูกต้องโดยสมบูรณ์ แล้ว \(\mathcal{D}(\boldsymbol{X}) \approx 0\) สำหรับทุก ๆ ภาพที่สร้างขึ้น และ พจน์ \(E_{\boldsymbol{X} \sim p_{\mathcal{G}}}[\log(1 - \mathcal{D}(\boldsymbol{X}))] \approx 0\). แต่หากโครงข่ายแบ่งแยก ทายผิด จะทำให้ได้ \(\log(0) \rightarrow -\infty\) หรือทำให้ได้ค่าที่ต่ำมาก ๆ.
หมายเหตุ สัญกรณ์ที่ในนิพจน์ \(\eqref{eq: convapp GAN opt prob}\) ใช้เพื่อความกระชับ. เช่นเดียวกับการฝึกโครงข่ายประสาทเทียมอื่น ๆ การฝึกโครงข่ายก่อกำเนิดและโครงข่ายแบ่งแยก ก็ดำเนินการผ่านการปรับค่าพารามิเตอร์ต่าง ๆ ของโครงข่าย. นั่นคือ หากจะเขียนนิพจน์ \(\eqref{eq: convapp GAN opt prob}\) ให้ละเอียดถูกต้องมากยิ่งขึ้น อาจเขียนเป็น \(\min_{\boldsymbol{\theta}} \max_{\boldsymbol{w}} V(\mathcal{G}_{\boldsymbol{\theta}}, \mathcal{D}_{\boldsymbol{w}})\) เมื่อโครงข่ายก่อกำเนิด \(\mathcal{G}_{\boldsymbol{\theta}}\) และโครงข่ายแบ่งแยก \(\mathcal{D}_{\boldsymbol{w}}\) ถูกควบคุมพฤติกรรมด้วยพารามิเตอร์ \(\boldsymbol{\theta}\) และ \(\boldsymbol{w}\) ตามลำดับ.
โครงข่ายแบ่งแยก \(\mathcal{D}\) จะถูกฝึกเพื่อให้ค่าฟังก์ชันจุดประสงค์นี้สูงที่สุด ผ่านกลไกการทำนาย \(\mathcal{D}(\boldsymbol{X})\). ในขณะที่ โครงข่ายก่อกำเนิด จะพยายามทำให้ค่าฟังก์ชันจุดประสงค์นี้ต่ำที่สุด โดยผ่านกลไก \(\boldsymbol{X} \sim p_{\mathcal{G}}\) ซึ่งคือ การสร้างภาพให้เหมือนภาพจริงที่สุด หรือพยายามเรียนรู้ให้การแจกแจง \(p_{\mathcal{G}}\) ใกล้เคียงกับ \(p_{data}\) มากที่สุด. โครงข่ายก่อกำเนิดในอุดมคติ จะมี \(p_{\mathcal{G}} \approx p_{data}\).
ปัจจัยสำคัญประการหนึ่งคือ โครงข่ายก่อกำเนิด \(\mathcal{G}\) ไม่ได้รับข้อมูลเกี่ยวกับภาพจริงโดยตรงเลย โครงข่ายก่อกำเนิด \(\mathcal{G}\) ถูกบังคับให้เรียนรู้การแจกแจงของภาพจริงผ่านปฏิสัมพันธ์กับโครงข่ายแบ่งแยก \(\mathcal{D}\). โครงข่ายแบ่งแยก \(\mathcal{D}\) เห็นทั้งภาพจริง และภาพที่สร้างขึ้น และได้รับเฉลยผ่านเกรเดียนต์หลังจากทายไป. อีกทอดหนึ่ง โครงข่ายก่อกำเนิด \(\mathcal{G}\) ก็ได้รับเกรเดียนต์ของมันผ่านเกรเดียนต์ของโครงข่ายแบ่งแยก \(\mathcal{D}\) อีกต่อหนึ่ง.
โครงข่ายก่อกำเนิด อาจถูกมองว่าเป็นการเรียนรู้ เพื่อที่จะแปลงข้อมูลจากปริภูมิของตัวแทนสุ่ม ที่อาจถูกเรียกว่า ปริภูมิตัวแทน (representation space) หรือปริภูมิซ่อนเร้น (latent space) ไปสู่ปริภูมิของข้อมูล. นั่นคือ \(\mathcal{G}: \boldsymbol{z} \rightarrow \boldsymbol{X}\) เมื่อ \(\boldsymbol{z}\) คือตัวแปรในปริภูมิซ่อนเร้น และ \(\boldsymbol{X}\) คือตัวแปรในปริภูมิข้อมูล. ส่วนโครงข่ายแบ่งแยกก็เป็นเสมือนการแปลงจากข้อมูลไปสู่ค่าระหว่างศูนย์กับหนึ่ง. นั่นคือ \(\mathcal{D}: \boldsymbol{X} \rightarrow (0,1)\). ภายหลังการฝึกเสร็จสิ้น โครงข่ายก่อกำเนิด \(\mathcal{G}\) สามารถนำไปใช้สร้างตัวอย่างข้อมูลได้ตามต้องการ.
7.2.2.0.1 โครงข่ายปรปักษ์เชิงสร้างแบบมีเงื่อนไข.
เมียร์ซะและคณะ ขยายความสามารถของโครงข่ายปรปักษ์เชิงสร้าง โดยใช้ความน่าจะเป็นแบบมีเงื่อนไข. โครงข่ายปรปักษ์เชิงสร้างที่มีความสามารถที่เพิ่มขึ้นมาเช่นนี้ ถูกเรียกว่า โครงข่ายปรปักษ์เชิงสร้างแบบมีเงื่อนไข (Conditional Generative Adversarial Networks). กระบวนการฝึกของโครงข่ายปรปักษ์เชิงสร้างแบบมีเงื่อนไข อาจตั้งจุดประสงค์เป็น \[\begin{eqnarray} \min_{\mathcal{G}} \max_{\mathcal{D}} V(\mathcal{G}, \mathcal{D}) &=& E_{\boldsymbol{X} \sim p_{data|\boldsymbol{C}}}[\log \mathcal{D}(\boldsymbol{X}|\boldsymbol{C})] + E_{\boldsymbol{X} \sim p_{\mathcal{G}|\boldsymbol{C}}}[\log(1 - \mathcal{D}(\boldsymbol{X}|\boldsymbol{C}))] \label{eq: convapp conditional GAN opt prob} \end{eqnarray}\] เมื่อ \(\mathcal{D}(\boldsymbol{X}|\boldsymbol{C})\) แทนผลการทำนายจากโครงข่ายแบ่งแยก ที่รับอินพุตหลักเป็น \(\boldsymbol{X}\) และรับอินพุตรองเป็น \(\boldsymbol{C}\) ซึ่งใช้ระบุเงื่อนไข. สัญกรณ์ \(\boldsymbol{X} \sim p_{data|\boldsymbol{C}}\) หมายถึง ตัวแปร \(\boldsymbol{X}\) มีการแจกแจงตามข้อมูลจริงที่เป็นไปตามเงื่อนไข \(\boldsymbol{C}\). สัญกรณ์ \(\boldsymbol{X} \sim p_{\mathcal{G}|\boldsymbol{C}}\) หมายถึง ตัวแปร \(\boldsymbol{X}\) มีการแจกแจงตามการแจกแจงจากโครงข่ายก่อกำเนิด ที่เงื่อนไข \(\boldsymbol{C}\). รูป 1.8 แสดงกลไกเพิ่มเติม เพื่อเพิ่มคุณสมบัติการใช้เงื่อนไข ให้กับโครงข่ายปรปักษ์เชิงสร้าง. โครงสร้างและรายละเอียดในการทำโครงข่ายปรปักษ์เชิงสร้างแบบมีเงื่อนไข อาจแตกต่างไปได้ เช่น อินโฟแกน (InfoGAN).

7.2.2.0.2 การประยุกต์ใช้โครงข่ายปรปักษ์เชิงสร้าง.
โครงข่ายปรปักษ์เชิงสร้าง เป็นพัฒนาการที่สำคัญสำหรับการเรียนรู้เชิงลึก และได้ทำให้เกิดการประยุกต์ใช้อย่างกว้างขวาง ขยายเข้าไปแม้แต่ในวงการศิลปะ. การศึกษาวิจัยและขอบเขตการใช้งานของโครงข่ายปรปักษ์เชิงสร้าง เป็นไปอย่างรวดเร็วและต่อเนื่อง จนโครงข่ายปรปักษ์เชิงสร้างเป็นเสมือนศาสตร์ย่อย ๆ ในตัวเอง. ตัวอย่างการประยุกต์ใช้ทั่ว ๆ ไปส่วนหนึ่งของโครงข่ายปรปักษ์เชิงสร้าง ได้แก่ การจำแนกกลุ่ม (เช่น การนำโครงข่ายแบ่งแยกไปใช้), การสกัดลักษณะสำคัญ (ซึ่งอาจจะได้จากทั้งค่าเอาต์พุตชั้นซ่อนภายในโครงสร้างของโครงข่ายแบ่งแยก หรืออาจจะได้จากการทำพีชคณิตเวกเตอร์ ที่จะอธิบายเพิิ่มเติมต่อไป), การสังเคราะห์ข้อมูล (ซึ่งคือ การสร้างข้อมูล โดยใช้โครงข่ายก่อกำเนิด และนี่คือ จุดประสงค์หลักของโครงข่ายปรปักษ์เชิงสร้าง), การแปลงรูปหนึ่งไปสู่อีกรูปหนึ่ง, การเพิ่มความละเอียดให้กับภาพ เป็นต้น.
คณะของรีด ใช้โครงข่ายปรปักษ์เชิงสร้าง ในการสร้างภาพขึ้นมาตามคำบรรยาย. โครงข่ายปรปักษ์เชิงสร้างอะไรที่ไหน (Genverative Adversarial What-Where Network) สามารถสร้างภาพขึ้นจากส่วนภาพเล็ก ๆ ที่แต่ละส่วนภาพสร้างขึ้นมาตามตำแหน่งที่กำหนด และตามลักษณะพืื้นผิวที่บรรยาย. นอกจากนั้น มีการใช้โครงข่ายปรปักษ์เชิงสร้างไปใช้ในกระบวนแก้ไขและตกแต่งรูป. การแปลงรูปหนึ่งไปสู่อีกรูปหนึ่ง ก็มีการประยุกต์ใช้ที่หลากหลาย เช่น การแปลงกระบวนแบบศิลปะ (artistic style transfer), การแปลงกระบวนแบบ (style transfer), การสร้างภาพเหมือนจริงตามส่วนภาพ ที่ศิลปินสามารถวาดภาพคร่าวแล้วให้โครงข่ายปรปักษ์เชิงสร้างช่วยเติมรายละเอียด (semantic image synthesis), การสร้างภาพล้อเลียนบุคคลอัตโนมัติ (automatic caricature generation), การเพิ่มอายุให้หน้า (age progression).
พีชคณิตเวกเตอร์ (Vector arithmetic) คือ การนำเวกเตอร์ค่าสุ่ม \(\boldsymbol{z}\) ที่เป็นอินพุตของโครงข่ายก่อกำเนิด สำหรับภาพต่าง ๆ มาทำบวกหรือลบกัน แล้วนำเวกเตอร์ผลลัพธ์เข้าไปเป็นอินพุตของโครงข่ายก่อกำเนิด ผลลัพธ์ที่ได้พบว่ามีลักษณะสำคัญจากภาพของเวกเตอร์ที่เป็นตัวถูกดำเนินการ ผสมกันในลักษณะเชิงเส้น. ตัวอย่างเช่น แรดฟอร์ดและคณะ เลือกภาพผู้หญิงยิ้มสามภาพออกมา แล้วหาเวกเตอร์เฉลี่ย \(\bar{\boldsymbol{z}}_{\mathrm{smile, woman}}\) จากเวกเตอร์ค่าสุ่มของภาพทั้งสาม นำไปลบออกด้วยเวกเตอร์เฉลี่ย \(\bar{\boldsymbol{z}}_{\mathrm{neutral, woman}}\) ที่เฉลี่ยจากเวกเตอร์ค่าสุ่มของภาพผู้หญิงหน้าเฉย (ไม่ได้ยิ้ม) แล้วนำไปบวกด้วยเวกเตอร์เฉลี่ย \(\bar{\boldsymbol{z}}_{\mathrm{neutral, man}}\) ที่เฉลี่ยจากเวกเตอร์ค่าสุ่มของภาพผู้ชายหน้าเฉย (ไม่ได้ยิ้ม) สุดท้ายนำเวกเตอร์ผลลัพธ์เข้าโครงข่ายก่อกำเนิด และรูปภาพที่สร้างขึ้นมา พบว่าเป็นภาพผู้ชายยิ้ม. นั่นคือ โครงข่ายก่อกำเนิด ได้เรียนรู้ที่จะเข้ารหัสลักษณะสำคัญของภาพไว้ในเวกเตอร์ค่าสุ่ม \(\boldsymbol{z}\) และการเข้ารหัสยังเป็นไปในลักษณะเชิงเส้น (จึงสามารถลบและบวก แล้วได้ผลลัพธ์ในลักษณะเชิงเส้นออกมา). ด้วยคุณสมบัติเช่นนี้ อาจมองว่าโครงข่ายก่อกำเนิดได้เรียนรู้ที่จะกำหนดความหมายของลักษณะสำคัญไว้ที่ค่าของเวกเตอร์ \(\boldsymbol{z}\). เนื่องจากความหมายของลักษณะสำคัญนี้ ไม่ได้ถูกกำหนดออกมาอย่างชัดเจน ต้องอาศัยการสืบการสังเกตจึงจะพอเห็นความเชื่อมโยง เวกเตอร์ \(\boldsymbol{z}\) บางครั้งจึงถูกเรียกเป็นลักษณะซ่อนเร้น (latent representation) และปริภูมิของ \(\boldsymbol{z}\) จึงมักถูกอ้างถึงเป็นปริภูมิซ่อนเร้น หรือปริภูมิตัวแทน ตามที่อภิปรายไปก่อนหน้า. รูป 1.9 แสดงภาพประกอบที่วาดขึ้น (ดูภาพจริงจาก ).

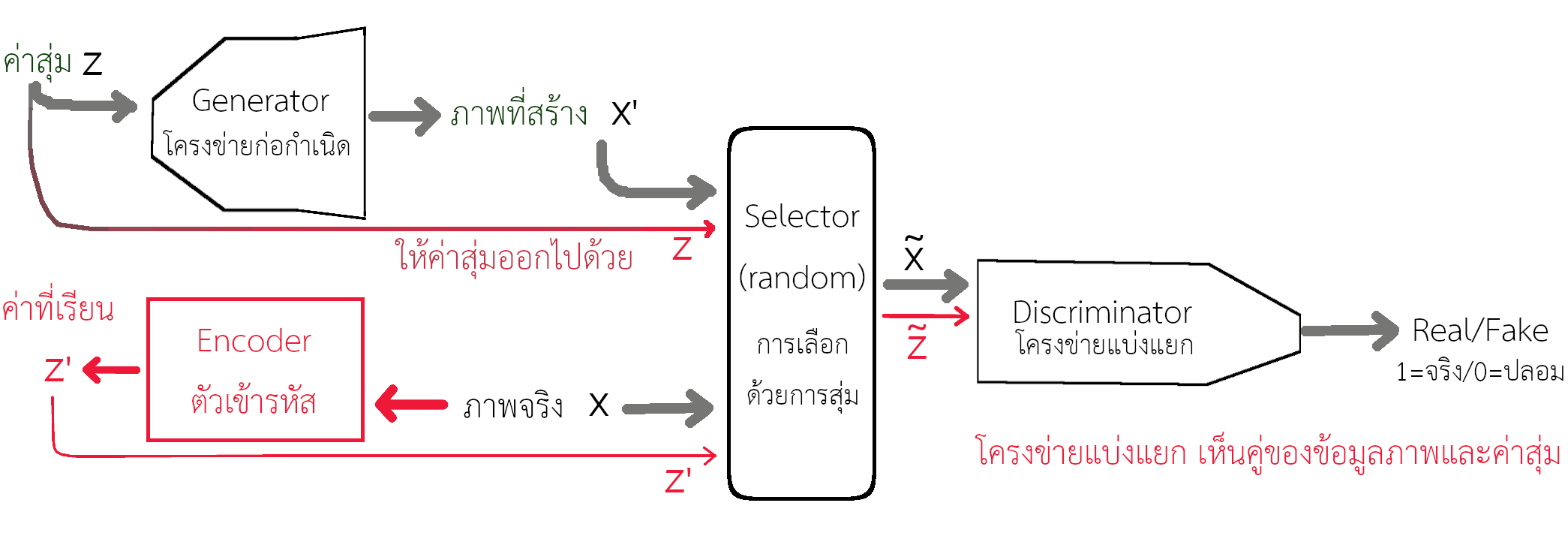
แม้ว่าโครงข่ายก่อกำเนิดที่ถูกฝึกมาดีแล้วจะสามารถแปลงค่าจากปริภูมิซ่อนเร้น ไปสู่ปริภูมิข้อมูลได้ แต่เช่นเดียวกับโครงข่ายประสาทเทียมทั่วไป คือ หากต้องการจะคำนวณย้อนกลับ ซึ่งคือการแปลงจากภาพ \(\boldsymbol{X}\) กลับมาเป็นเวกเตอร์ซ่อนเร้น \(\boldsymbol{z}\) นั้น ไม่สามารถทำได้โดยตรง. อย่างไรก็ตาม มีความพยายามที่จะเพิ่มกลไกภายใน เพื่อให้โครงข่ายปรปักษ์เชิงสร้างสามารถคำนวณกลับไปกลับมาระหว่างปริภูมิซ่อนเร้น และปริภูมิข้อมูลได้. รูป 1.10 แสดงโครงสร้างของไบแกน (BiGAN). การอนุมานที่เรียนเชิงปรปักษ์ (Adversarially learned inference คำย่อ ALI) ซึ่งเป็นแนวคิดเดียวกันกับไบแกน ก็ถูกเสนอในช่วงเวลาเดียวกัน. กลไกที่สำคัญ สำหรับทั้งไบแกนและการอนุมานที่เรียนเชิงปรปักษ์ คือ การเพิ่มตัวเข้ารหัส (encoder) เพื่อเรียนรู้ความสัมพันธ์ระหว่างปริภูมิซ่อนเร้นและปริภูมิข้อมูล. หากจำเพาะลงไปก็คือ ตัวเข้ารหัส ทำหน้าที่เรียนรู้การแจกแจงแบบมีเงื่อนไข \(p(\boldsymbol{z}|\boldsymbol{X})\) เมื่อ \(\boldsymbol{X}\) แทนข้อมูลภาพ และ \(\boldsymbol{z}\) คือ ค่าลักษณะซ่อนเร้น ที่โครงข่ายก่อกำเนิดใช้. อย่างไรก็ตาม เครสเวลและคณะ ให้ความเห็นว่า ภาพที่สร้างจากไบแกนหรือการอนุมานที่เรียนเชิงปรปักษ์ยังมีคุณภาพค่อนข้างต่ำ. นั่นอาจหมายถึงว่า การศึกษาวิจัย ถึงกลไกแปลงกลับจากปริภูมิข้อมูลไปสู่ปริภูมิซ่อนเร้น ในโครงข่ายปรปักษ์เชิงสร้าง ยังอยู่ในขั้นเริ่มต้นเท่านั้น.
7.2.2.0.3 ปัญหาในการฝึก.
การฝึกโครงข่ายปรปักษ์เชิงสร้าง ถูกรายงาน ว่าทำได้ยาก และมีโอกาสล้มเหลวสูงมาก จากหลาย ๆ สาเหตุ รวมถึง
การลู่เข้ายาก ที่นักวิจัยมักพบว่า มันยากที่ทำให้การฝึกโครงข่ายก่อกำเนิด ลู่เข้า. ปัญหานี้ ส่วนหนึ่งอาจมาจากธรรมชาติของข้อมูลภาพ. ข้อมูลภาพมีปริภูมิที่ขนาดใหญ่มาก ๆ (รูปสีขนาด \(W \times H\) พิกเซล เทียบเท่าจุดข้อมูลในปริภูมิขนาด \(3 \cdot W \cdot H\) มิติ) แต่ตัวอย่างข้อมูลต่าง ๆ ที่มี (เช่น ภาพจริงต่าง ๆ) เป็นข้อมูลสำหรับการสนับสนุนของฟังก์ชันความหนาแน่นความน่าจะเป็น 6 ครอบคลุมเพียงบริเวณเล็ก ๆ ในปริภูมิ และเมื่อเทียบกับขนาดของปริภูมิทั้งหมดแล้ว บริเวณที่ครอบคลุมมีขนาดเล็กมาก ๆ. กล่าวคือ แม้จะใช้ตัวอย่างข้อมูลจำนวนมากแล้ว แต่จำนวนตัวอย่างที่ใช้ ก็ยังน้อยมากเมื่อเทียบกับขนาดประชากร (โอกาสทั้งหมดที่เป็นไปได้ของข้อมูล) และตัวอย่างข้อมูลเหล่านี้ ก็ยากที่จะเป็นตัวแทนที่พอเพียงได้.
นอกจากนั้น ยังมีการศึกษา ที่พบว่า ก่อนการฝึก การแจกแจงก่อกำเนิด \(p_{\mathcal{G}}\) อาจจะไม่มีการซ้อนทับกับการแจกแจงเป้าหมาย \(p_{data}\) เลย. หากเป็นเช่นนั้นจริง ผลคือ โครงข่ายแบ่งแยกจะสามารถถูกฝึกได้อย่างง่ายดายและรวดเร็ว เพื่อที่จะสามารถจำแนกตัวอย่างจริง \(\boldsymbol{X} \sim p_{data}\) ออกจากตัวอย่างปลอม \(\boldsymbol{X} \sim p_{\mathcal{G}}\) ได้อย่างแม่นยำสมบูรณ์ (ความแม่นยำ \(100\%\)) นั่นคือ การฝึกโครงข่ายแบ่งแยกจะลู่เข้าจน ฟังก์ชันจุดประสงค์มีค่าเป็นศูนย์ ได้อย่างรวดเร็ว และส่งผลให้เกรเดียนต์ต่าง ๆ เป็นศูนย์ ซึ่งจะทำให้การฝึกโครงข่ายกำเนิดไม่สามารถทำต่อไปได้.
อีกประเด็นหนึ่ง เครสเวลและคณะ อภิปรายประเด็นจากการศึกษาทฤษฎีโครงข่ายปรปักษ์เชิงสร้าง กับฟังก์ชันจุดประสงค์ที่ใช้ ว่า หากโครงข่ายแบ่งแยกไม่ได้อยู่ในสภาพที่ดีที่สุดแล้ว การฝึกโครงข่ายกำเนิดก็อาจจะไม่แม่นยำ หรืออาจได้ผลลัพธ์ผิดความหมายได้. นี่อาจหมายถึง ความจำเป็นในการออกแบบฟังก์ชันจุดประสงค์ใหม่ สำหรับโครงข่ายปรปักษ์เชิงสร้าง. อย่างไรก็ตาม ด้วยฟังก์ชันจุดประสงค์ดังเช่นนิพจน์ \(\eqref{eq: convapp GAN obj function}\) ประเด็นนี้ ที่เมื่อประกอบกับข้ออภิปรายข้างต้นแล้ว จะช่วยให้เห็นความยากของการฝึกโครงข่ายปรปักษ์เชิงสร้าง ที่หากโครงข่ายแบ่งแยกทำงานได้ดีเกินไป การฝึกโครงข่ายกำเนิดก็จะทำได้ยาก หรืออาจล้มเหลว และหากโครงข่ายแบ่งแยกทำงานไม่ดีเลย การฝึกโครงข่ายกำเนิดก็จะไปผิดทาง.
การพังทลายของภาวะ (mode collapse) ที่หมายถึง โครงข่ายกำเนิดสร้างแต่เอาต์พุตที่เหมือน ๆ กัน แม้ว่าจะรับอินพุตต่างกัน. จุดประสงค์ คือ ต้องการได้โครงข่ายกำเนิดที่สามารถสร้างแต่เอาต์พุตออกมาได้ โดยเอาต์พุตที่ได้ มีการแจกแจงคล้ายข้อมูลจริงมากที่สุด. ตัวอย่างเช่น แทนที่โครงข่ายกำเนิดจะสามารถสร้างภาพเหมือนจริงใหม่ ๆ ออกมาได้เรื่อย ๆ แต่โครงข่ายกำเนิดกลับสร้างภาพเหมือนจริงภาพเดิม ๆ ออกมา แม้ว่าจะรับอินพุต (ซึ่งคือค่าสุ่ม) ค่าใหม่แล้วก็ตาม.
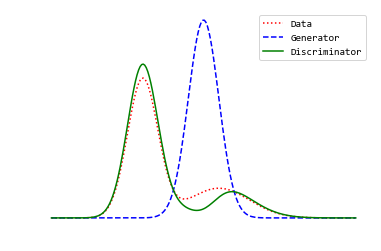
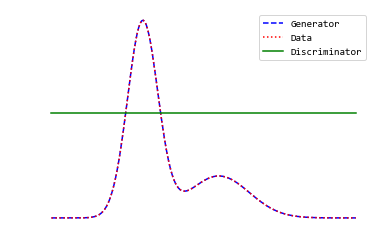
การฝึกโครงข่ายแบ่งแยกได้เร็วและดีเกินไป. หากโครงข่ายแบ่งแยกทำงานได้ดีมาก ๆ อาจทำให้ \(V(\mathcal{G}, \mathcal{D}) \approx 0\) ซึ่งมีผลให้เกรเดียนต์มีค่าใกล้ศูนย์ และทำให้การฝึกโครงข่ายก่อกำเนิดทำได้ยากมาก หรืออาจล้มเหลวได้. รูป 1.13 แสดงสมมติฐานกลไกการเรียนรู้การแจกแจงของโครงข่ายปรปักษ์เชิงสร้าง ในสถานการณ์ต่าง ๆ.
แม้มองผิวเผินอาจจะดูดี แต่การฝึกโครงข่ายแบ่งแยกให้ได้สมบูรณ์ก่อน (เมื่อเทียบกับความสามารถของโครงข่ายก่อกำเนิด) แล้วจึงค่อยฝึกโครงข่ายก่อกำเนิด ไม่ใช่แนวทางที่นิยมปฏิบัติ ด้วยเหตุผลข้างต้น. แนวทางปฏิบัติที่นิยมคือ การฝึกโครงข่ายแบ่งแยกไปก่อนระยะหนึ่ง แล้วจึงค่อยฝึกโครงข่ายก่อกำเนิดไปพร้อม ๆ กัน. นอกจากนั้น ด้วยเหตุผลด้านเสถียรภาพเชิงตัวเลข ในการฝึกโครงข่ายก่อกำเนิด มักนิยมใช้จุดประสงค์ \(\max_{\mathcal{G}} E_{\boldsymbol{X} \sim p_{\mathcal{G}}} [\log \mathcal{D}(\boldsymbol{X})]\) มากกว่า \(\min_{\mathcal{G}} E_{\boldsymbol{X} \sim p_{\mathcal{G}}} [\log(1 - \mathcal{D}(\boldsymbol{X}))]\).
 |
 |
 |
| (ก) | (ข) | (ค) |
7.2.2.0.4 เทคนิคในการฝึกโครงข่ายปรปักษ์เชิงสร้าง.
จากความท้าทายในการฝึกโครงข่ายปรปักษ์เชิงสร้างที่อภิปรายข้างต้น แรดฟอร์ดและคณะ ได้เสนอดีซีแกน (DCGAN จาก Deep Convolutional Generative Adversarial Networks) เพื่อบรรเทาปัญหา. ดีซีแกน มีปัจจัยที่สำคัญคือ (1) การใช้คอนโวลูชั่นก้าวยาว (strided convolution) แทนการใช้ชั้นดึงรวม ในโครงสร้างของโครงข่ายแบ่งแยก \(\mathcal{D}\). คอนโวลูชั่นก้าวยาว หมายถึง ชั้นคอนโวลูชัันที่ใช้ก้าวย่างขนาดใหญ่กว่าหนึ่ง เช่น การใช้ขนาดก้าวย่าง \(S = 2\). ผลลัพธ์ของการใช้คอนโวลูชั่นก้าวยาว จะให้ผลเหมือนการลดขนาดแผนที่ลักษณะสำคัญลง (หรือ spatially downsampling). (2) การใช้ชั้นคอนโวลูชั่น โดยเฉพาะใช้การทำคอนโวลูชั่นก้าวเศษ (fractionally-strided convolution หรือ transposed convolution) ในโครงสร้างของโครงข่ายก่อกำเนิด \(\mathcal{G}\).
หากจะอธิบายโดยง่ายแล้ว ภายใต้บริบทนี้ คอนโวลูชั่นก้าวเศษ ก็คือ การขยายขนาดแผนที่ลักษณะสำคัญที่เป็นอินพุต แล้วจึงทำการคำนวณคอนโวลูชั่น. การขยายขนาดแผนที่ลักษณะสำคัญ (ซึ่งขยายเฉพาะในมิติลำดับเชิงพื้นที่) ทำด้วยการเติมค่าศูนย์เข้าไประหว่างค่าพิกเซลเดิม (รวมการเติมเต็มด้วยศูนย์ ที่เติมค่าศูนย์ที่บริเวณขอบของแผนที่ด้วย). ผลลัพธ์ของการใช้คอนโวลูชั่นก้าวเศษ จะให้ผลเหมือนการเพิ่มขนาดแผนที่ลักษณะสำคัญขึ้น (หรือ spatially upsampling). รูป 1.14 แสดงกลไกที่คอนโวลูชั่นก้าวเศษ ช่วยขยายขนาดแผนที่ลักษณะสำคัญขึ้น. หากสังเกตการทำคอนโวลูชั่นในรูป เมื่อมองจากปฏิสัมพันธ์ระหว่างฟิลเตอร์และอินพุต อาจดูเหมือนกับว่าฟิลเตอร์ขยับผ่านพิกเซลช้าลง คล้ายกับว่า ใช้ขนาดก้าวย่างที่เล็กกว่าหนึ่ง ซึ่งเป็นที่มาของชื่อ คอนโวลูชั่นก้าวเศษ.

หมายเหตุ คอนโวลูชั่นก้าวเศษ บางครั้งอาจถูกเรียก คอนโวลูชั่นสลับเปลี่ยน (Transposed convolution) ซึ่งมาจากการตีความทางคณิตศาสตร์. นั่นคือ หากดำเนินคอนโวลูชั่นด้วยการแปลงอินพุตและค่าน้ำหนักของฟิลเตอร์เป็นเมทริกซ์ โดยจัดรูปเมทริกซ์ทั้งสองให้ถูกต้อง (มีการใช้ค่าซ้ำและมีการเติมศูนย์เข้าไป ดูแบบฝึกหัด [ex: CNN implementation] ประกอบ) ซึ่งทำให้ได้เมทริกซ์ของค่าน้ำหนักเป็น เมทริกซ์มากเลขศูนย์ (sparse matrix) แล้ว การทำคอนโวลูชั่น ก็เหมือนกับการคูณเมทริกซ์อินพุตเข้ากับเมทริกซ์ค่าน้ำหนัก แล้วนำผลลัพธ์ที่ได้ไปจัดรูปให้เข้ากับโครงสร้างที่ถูกต้อง. ในทำนองเดียวกัน คอนโวลูชั่นก้าวเศษ ก็เสมือนการคูณเมทริกซ์อินพุตเข้ากับการสลับเปลี่ยนของเมทริกซ์ค่าน้ำหนัก. ดังนั้น กระบวนการนี้จึงเรียกว่า คอนโวลูชั่นสลับเปลี่ยน. (ศึกษาเพิ่มเติมได้จาก )
คอนโวลูชั่นก้าวเศษ บางครั้ง อาจถูกเรียกว่า การถอดคอนโวลูชั่น (Deconvolution). อย่างไรก็ตาม การถอดคอนโวลูชั่น มีความหมายอื่น (ซึ่งเป็นคนละเรื่อง) และถูกยอมรับมากกว่า. ความหมายที่ถูกยอมรับมากกว่าของการถอดคอนโวลูชั่น คือ การถอดพารามิเตอร์ของโครงข่ายคอนโวลูชั่นย้อนกลับ เพื่อศึกษากลไกการทำงานของโครงข่ายคอนโวลูชั่น ว่า ฟิลเตอร์แต่ละตัวที่ใช้ในโครงข่ายคอนโวลูชั่น ได้เรียนรู้เพื่อจะตรวจจับลักษณะรูปแบบเช่นไร. สำหรับการถอดคอนโวลูชั่น ในความหมายที่นิยมนี้ สามารถศึกษาเพิ่มเติมได้จากบทความ เป็นต้น.
นอกจากการใช้คอนโวลูชั่นก้าวยาวและคอนโวลูชั่นก้าวเศษในโครงสร้างของโครงข่ายแบ่งแยกและโครงข่ายก่อกำเนิดแล้ว แรดฟอร์ดและคณะ ยังแนะนำการใช้แบชนอร์ม (หัวข้อ [sec: batch norm]), แนะนำใช้ชั้นคอนโวลูชั่นลึก ๆ (หลาย ๆ ชั้น) แทนการใช้ชั้นเชื่อมต่อเต็มที่ 7, แนะนำการใช้เรลู สำหรับฟังก์ชันกระตุ้นของทุก ๆ ชั้นคำนวณในโครงข่ายก่อกำเนิด ยกเว้นชั้นเอาต์พุตที่แนะนำให้ใช้ไฮเปอร์บอลิกแทนเจนต์, แนะนำการใช้เรลูรั่ว สำหรับฟังก์ชันกระตุ้นของทุก ๆ ชั้นคำนวณในโครงข่ายแบ่งแยก.
เทคนิคอื่น ๆ ที่มีรายงานว่า เป็นปัจจัยสำคัญช่วยการฝึกโครงข่ายปรปักษ์เชิงสร้าง ได้แก่ การจับคู่ลักษณะสำคัญ, การแยกแยะหมู่เล็ก, การเฉลี่ยตามประวัติ, การทำฉลากราบรื่นทางเดียว, การทำหมู่เล็กเสมือนจริง, การใส่สัญญาณรบกวน ไปจนถึงการเปลี่ยนฟังก์ชันจุดประสงค์ (ดู เพิ่มเติม) เป็นต้น. เครสเวลและคณะ ให้ความเห็นว่า โครงข่ายปรปักษ์เชิงสร้างที่ฝึกได้ง่ายที่สุด น่าจะเป็นแบบจำลองที่เสนอโดยคณะของอาร์โจฟสกี หรือของคณะของมาคฮ์ซานี.
การจับคู่ลักษณะสำคัญ (feature matching) เปลี่ยนฟังก์ชันจุดประสงค์สำหรับโครงข่ายก่อกำเนิด เป็น \(\min_{\mathcal{G}} \| E_{\boldsymbol{X} \sim p_{data}}[\boldsymbol{f}(\boldsymbol{X})] - E_{\boldsymbol{X} \sim p_{\mathcal{G}}}[\boldsymbol{f}(\boldsymbol{X})] \|^2_2\) เมื่อ \(\boldsymbol{f}(\boldsymbol{X})\) เป็นลักษณะสำคัญที่ได้จากโครงข่ายแบ่งแยก (ค่าเวกเตอร์ของชั้นคำนวณชั้นหนึ่งที่อยู่ภายในโครงสร้างของโครงข่ายแบ่งแยก) ในขณะที่ยังใช้ฟังก์ชันจุดประสงค์แบบเดิมสำหรับโครงข่ายแบ่งแยก (เช่น \(\max_{\mathcal{D}} V(\mathcal{G}, \mathcal{D}) = E_{\boldsymbol{X} \sim p_{data}}[\log \mathcal{D}(\boldsymbol{X})] + E_{\boldsymbol{X} \sim p_{\mathcal{G}}}[\log(1 - \mathcal{D}(\boldsymbol{X}))]\)).
การแยกแยะหมู่เล็ก (minibatch discrimination) เพิ่มสัญญาณสารสนเทศ ที่ช่วยบอกโครงข่ายแยกแยะว่าอินพุตที่ได้ เหมือนหรือแตกต่างจากอินพุตอื่นในหมู่เล็กมากน้อยขนาดไหน. ดังนั้น โครงข่ายแยกแยะจะสามารถระบุอินพุตปลอมที่มีปัญหาโครงข่ายแยกแยะได้อย่างง่ายดาย.
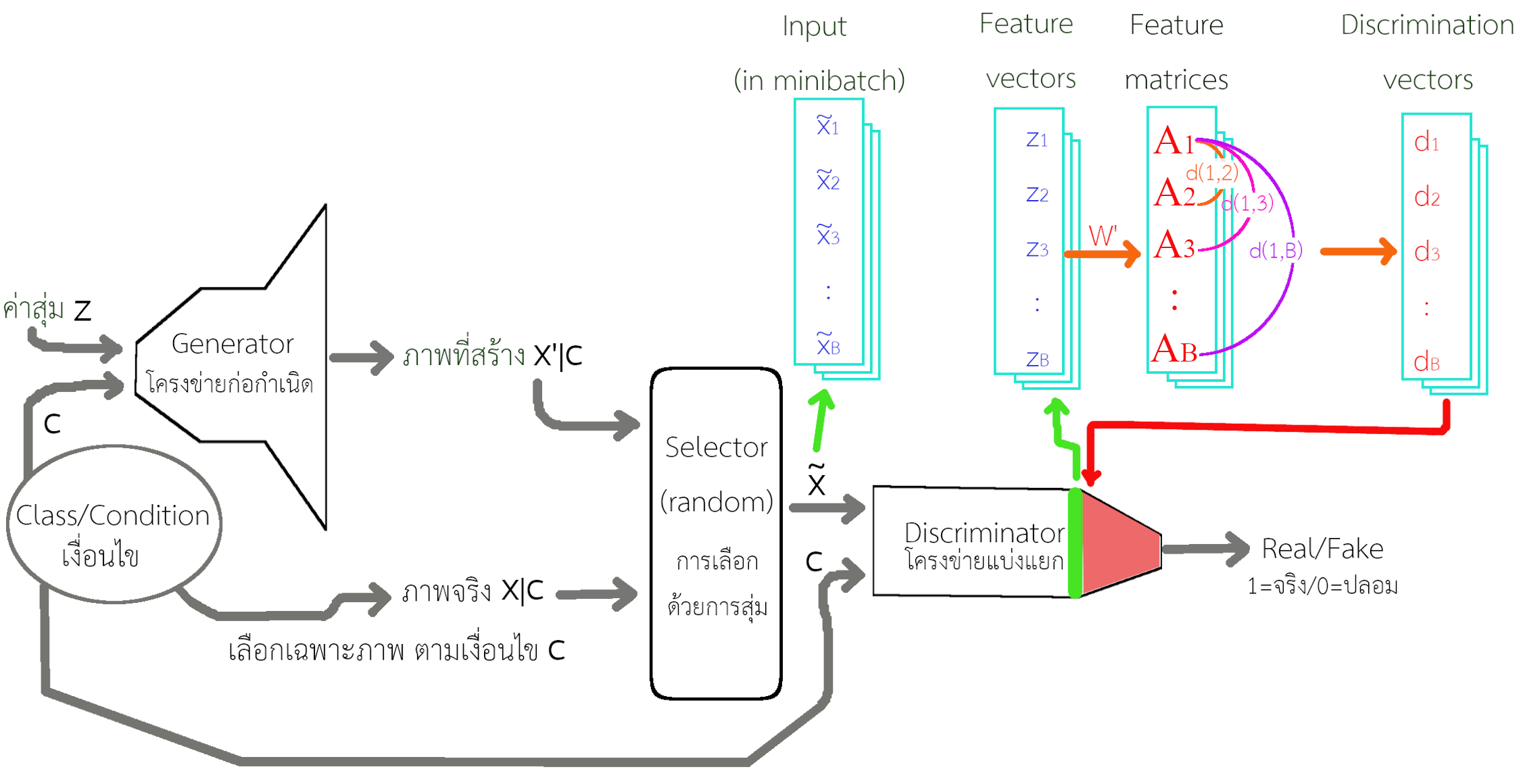
รูป 1.15 แสดงกลไกของการแยกแยะหมู่เล็ก. คณะของแซลลิมันส์ แปลงเวกเตอร์ลักษณะสำคัญ \(\boldsymbol{z}_n \in \mathbb{R}^M\) (เลือกจากชั้นคำนวณในโครงข่ายแยกแยะ และ \(M\) เป็นขนาดของเวกเตอร์) ให้เป็นเมทริกซ์ลักษณะสำคัญ \(\boldsymbol{A}_n \in \mathbb{R}^{P \times Q}\) (ด้วยการคูณกับเทนเซอร์ค่าน้ำหนัก \(\boldsymbol{W}'\) ที่ปรับค่าได้ในกระบวนการฝึก) เมื่อ \(P\) และ \(Q\) เป็นจำนวนแถวและสดมภ์ที่ต้องการ. ความต่างระหว่างเมทริกซ์ลักษณะสำคัญ ถูกระบุด้วยเวกเตอร์ \(\boldsymbol{d}(i,j) \in \mathbb{R}^P\) ที่มีส่วนประกอบ \(d_r(i,j) = \exp( - \| \mathrm{row}_r(\boldsymbol{A}_i) - \mathrm{row}_r(\boldsymbol{A}_j)\|_1)\) สำหรับ \(r = 1, \ldots, P\) เมื่อ ดัชนีของตัวอย่างในหมู่เล็ก \(i, j \in \{1, \ldots, B\}\) และ \(B\) คือจำนวนตัวอย่างในหมู่เล็ก. ตัวดำเนินการ \(\mathrm{row}_r(\boldsymbol{A})\) หมายถึง แถวที่ \(r^{th}\) ของเมทริกซ์ \(\boldsymbol{A}\) และ \(\| [v_1, v_2, \ldots, v_N]^T \|_1 = \sum_{n=1}^N |v_n|\) หรือ \(L^1\) นอร์ม (L1 norm). ความต่างระหว่างเมทริกซ์ ถูกสรุปเป็นเวกเตอร์แยกแยะ \(\boldsymbol{d}_i = [\sum_{j=1}^B \boldsymbol{d}_1(i,j), \ldots, \sum_{j=1}^B \boldsymbol{d}_P(i,j)]^T\) และค่าเวกเตอร์ \(\boldsymbol{d}_i\) ถูกป้อนร่วมกับเวกเตอร์ลักษณะสำคัญ \(\boldsymbol{z}_i\) (สำหรับตัวอย่างที่ \(i^{th}\) ในหมู่เล็ก) เข้าไปสู่ชั้นคำนวณต่อไปในโครงข่ายแบ่งแยก.
การเฉลี่ยตามประวัติ (historical averaging) เป็นการเพิ่มพจน์ที่ช่วยลดการเปลี่ยนค่าพารามิเตอร์อย่างรุนแรงในระหว่างการฝึก เพื่อช่วยให้ระบบเข้าสู่สมดุลย์ได้ง่ายขึ้น. ตัวอย่างเช่น คณะของแซลลิมันส์ ซึ่งได้รับแรงบัลดาลใจจากทฤษฎีเกม (game theory) เพิ่มพจน์ \(\| \boldsymbol{\theta} - \frac{1}{T} \sum_{i=1}^T \boldsymbol{\theta}^{(i)} \|^2\) เข้าไปในฟังก์ชันสูญเสียเดิม โดย \(\boldsymbol{\theta}\) แทนค่าปัจจุบันของพารามิเตอร์ต่าง ๆ ส่วน \(\boldsymbol{\theta}^{(i)}\) แทนค่าในสมัยฝึกที่ \(i^{th}\) ของพารามิเตอร์ต่าง ๆ และ \(T\) คือจำนวนสมัยฝึกที่ผ่านมา. พจน์ที่คณะของแซลลิมันส์ เพิ่มเข้าไปเป็นระยะทางยูคลีเดียน ระหว่างค่าพารามิเตอร์ปัจจุบัน กับค่าเฉลี่ยที่ผ่านมา. การเพิ่มพจน์นี้เข้าไปในฟังก์ชันสูญเสีย ส่งผลให้กระบวนการฝึกลดการปรับค่าพารามิเตอร์อย่างมากลงได้. อย่างไรก็ตามการใช้การเฉลี่ยตามประวัติ ควรทำอย่างระมัดระวัง และควรเลือกค่าน้ำหนักเพื่อรักษาดุลย์ระหว่างค่าฟังก์ชันสูญเสียเดิม กับค่าของพจน์การเฉลี่ยตามประวัตินี้อย่างเหมาะสม.
การทำฉลากราบรื่นทางเดียว (one-sided label smoothing) คือ การเปลี่ยนค่าเป้าหมายของฉลากเฉลยของโครงข่ายแบ่งแยก จากเฉลยว่าเป็นภาพจริง \(y = 1\) ลดลงเป็น \(1 - \epsilon\) แต่คงค่าเฉลยภาพปลอม \(y = 0\) ไว้เหมือนเดิม เช่น เปลี่ยนจากเฉลยภาพจริง จากค่า \(1\) เป็น \(0.9\) (\(\epsilon = 0.1\)). เทคนิคนี้ดัดแปลงมาจากการทำฉลากราบรื่น (label smoothing) เพื่อป้องกันไม่ได้โครงข่ายแบ่งแยกมีความมั่นใจมากเกินไป.
การทำฉลากราบรื่น เป็นเทคนิคที่เปลี่ยนค่าเป้าหมายของฉลากเฉลย เพื่อป้องกันไม่ให้แบบจำลองมีความมั่นใจมากเกินไป (over-confidence). การทำฉลากราบรื่น ดั่งเดิมออกแบบมาสำหรับการจำแนกกลุ่ม (multi-class classification) โดยการปรับค่าเป้าหมายของฉลากเฉลยสำหรับประเภท \(k^{th}\) เป็น \(q_k = (1 - \epsilon) y_k + \epsilon p(k)\) เมื่อ \(y_k\) คือค่าฉลากเฉลยของประเภท \(k^{th}\) (อยู่ในรูปรหัสหนึ่งร้อน นั่นคือ \(y_k = 1\) เมื่อเฉลยคือชนิด \(k^{th}\) และ \(y_k = 0\) เมื่อเฉลยไม่ใช่ชนิด \(k^{th}\)) และ \(p(k)\) คือการแจกแจงของข้อมูลชนิด \(k^{th}\) ส่วน \(\epsilon\) คืออภิมานพารามิเตอร์ที่เลือกได้ตามความเหมาะสม.
เซเจดีและคณะ เลือกประมาณ \(p(k)\) ด้วยการแจกแจงเอกรูป นั่นคือ ค่าฉลากเฉลย \(q_k = (1 - \epsilon) y_k + \frac{\epsilon}{K}\) เมื่อ \(K\) คือจำนวนประเภททั้งหมด. ตัวอย่างเช่น กรณีการจำแนก \(5\) ประเภท แล้วเลือก \(\epsilon = 0.1\) ค่าเป้าหมาย จะถูกปรับเป็น \(0.92\) สำหรับประเภทที่ถูกต้อง และ \(0.02\) สำหรับประเภทที่ไม่ถูกต้อง. ดังนั้นแบบจำลองที่ถูกฝึกอย่างดีแล้วจะปรับค่าทำนายเข้ามาที่ \(0.92\) ซึ่งอาจตีความว่ามั่นใจมาก แต่ไม่ร้อยเปอร์เซ็นต์ มีเผื่อใจไว้บ้าง ซึ่งหากมองเชิงการคำนวณ การปรับค่าฉลากเฉลยจะช่วยป้องกันไม่ให้แบบจำลองถูกปรับค่าเข้าไปสู่ช่วงอิ่มตัว (saturation region). แบบจำลองที่ถูกปรับค่าเข้าไปสู่ช่วงอิ่มตัว จะทำให้การฝึกต่อทำได้ยาก และให้ผลคล้ายการเกิดโอเวอร์ฟิต. (ดูแบบฝึกหัด [ex: label smoothing] เพิ่มเติมสำหรับการทำฉลากราบรื่น)
เพื่อลดการขึ้นกับข้อมูลภายในหมู่เล็กมากเกินไป เมื่อใช้แบชนอร์ม คณะของแซลลิมันส์ ใช้การทำหมู่เล็กเสมือนจริง (virtual minibatch) ทำแบชนอร์มกับจุดข้อมูล โดยใช้ค่าสถิติที่คำนวณจากจุดข้อมูลนั้น ๆ และหมู่อ้างอิง (reference batch) ซึ่งหมู่อ้างอิง ถูกเลือกขึ้นมาก่อนการฝึก และใช้หมู่นี้ตลอด (ไม่มีการเปลี่ยนแปลง). เนื่องจากการทำหมู่เล็กเสมือนจริง ทำการคำนวณมากขึ้น เพราะว่า ต้องทำการคำนวณไปข้างหน้า (forward pass) สำหรับสองหมู่เล็ก ดังนั้นคณะของแซลลิมันส์ จึงใช้การทำหมู่เล็กเสมือนจริงเฉพาะกับการฝึกโครงข่ายก่อกำเนิด
การใส่สัญญาณรบกวน (noise addition) คือการใส่สัญญาณรบกวน เช่น สัญญาณรบกวนที่มีการแจกแจงแบบเกาส์เซียน เข้าไปในทั้งภาพจริง และภาพที่สร้างจากโครงข่ายก่อกำเนิด. ซอนเดอบายและคณะ อ้างว่าการใส่สัญญาณรบกวน ให้ผลดีกว่าการทำฉลากราบรื่นทางเดียว. การใส่สัญญาณรบกวนเข้าไปกับทั้งภาพจริงและภาพปลอม เป็นคล้าย ๆ กับการปรับการแจกแจงจริง กับการแจกแจงจากโครงข่ายก่อกำเนิดให้เข้ามาใกล้กันและกันมากขึ้น.
7.2.2.0.5 เกร็ดความรู้ รูปแบบ“ประหลาด”ของจิต
“The most difficult subjects can be explained to the most slow-witted man if he has not formed any idea of them already; but the simplest thing cannot be made clear to the most intelligent man if he is firmly persuaded that he knows already, without a shadow of doubt, what is laid before him.”
—Leo Tolstoy
“เรื่องที่ยากที่สุดสามารถอธิบายให้คนที่หัวช้าที่สุดเข้าใจได้ ถ้าเขาไม่ฝังใจคิดไปเองก่อนแล้ว. แต่เรื่องที่ง่ายที่สุดไม่อาจจะอธิบายให้คนที่ฉลาดที่สุดเข้าใจได้ ถ้าเขามัวยึดติดสิ่งที่เขาคิด โดยที่ไม่สนใจความจริงที่อยู่ตรงหน้าเลยสักนิด.”
—ลิโอ โตล์สตอย
แม้ว่า ความเชื่อหลักในวงการแพทย์ เชื่อว่า (1) จิตเกิดจากสมอง และ (2) ชีวิตสิ้นสุดเมื่อคนตาย. แนวคิดนี้ เอ็ดเวิร์ด เคลลี่ เรียกว่า กายภาพนิยม (physicalism). กายภาพนิยม เป็นกรอบความคิด และมุมมองโลกที่มองว่า ทุกอย่างเป็นกายภาพ. นั่นรวมถึง ความคิดที่ว่า จิตก็เกิดมาจากกิจกรรมของสมอง สติและความรู้ตัวก็เป็นผลพลอยได้จากกิจกรรมของเซลล์ประสาท และเนื่องจากแนวคิดนี้เชื่อว่า จิตมาจากสมอง ดังนั้นเมื่อตัวตาย สมองหยุดทำงาน จิตจะจบหายไป. และถึงแม้ว่าคนส่วนใหญ่ก็เชื่อเช่นนั้น แต่แนวคิดนี้ก็ไม่ได้ถูกพิสูจน์ หรือทดสอบอย่างเป็นทางการเลย จนกระทั่งงานศึกษาที่สำคัญของพาร์เนียและคณะ กับทีมของแวนโลมเมล.
แซม พาร์เนีย เป็นแพทย์โรคหัวใจ ซึ่งเชี่ยวชาญในการกู้ชีพผู้ป่วยหัวใจวาย เนื่องจากต้องการลดความเสี่ยงภาวะเจ้าชายนิทราของผู้ป่วย พาร์เนียจึงได้ศึกษาวิจัยเกี่ยวกับสติรู้ตัว (consciousness) และรวมไปถึง การศึกษาประสบการณ์เฉียดตาย (Near Death Experience คำย่อ NDE) ของผู้ป่วย.
ประสบการณ์เฉียดตาย เป็นประสบการณ์การรับรู้ของผู้ป่วยที่อยู่ในสถานการณ์ที่ใกล้จะตาย หรือหลายครั้งผู้ป่วยหยุดหายใจ หัวใจหยุดเต้น และไม่มีกิจกรรมทางสมองแล้ว แต่แพทย์ พยาบาล เจ้าหน้าที่ สามารถกู้ชีพกลับมาได้. แม้ชื่อจะบอกว่าเป็น ประสบการณ์เฉียดตาย แต่จริง ๆ แล้ว ส่วนใหญ่ผู้ที่มีประสบการณ์นี้ ก็คือ ผู้ป่วยที่ได้ตายไปแล้วในช่วงเวลาสั้น ๆ แต่ได้รับการกู้ชีพกลับมาสำเร็จ. ถึงแม้ จะมีรายงานประสบการณ์เฉียดตาย จากอาการป่วยหลากหลายประเภท แต่งานวิจัยของพาร์เนียและคณะจะเน้นที่กลุ่มผู้ป่วยภาวะหัวใจวาย.
จากงานวิจัย พาร์เนียและคณะพบว่า ในจำนวนผู้ป่วยที่รอดชีวิตและให้สัมภาษณ์ มีราว ๆ 46% ที่มีความทรงจำ โดย 9% จัดเป็นประสบการณ์เฉียดตาย (ตามเงื่อนไขที่กำหนดในงานวิจัย). มี 2% ที่รู้ตัว โดย“เห็น” หรือ “ได้ยิน” เหตุการณ์เกี่ยวกับการกู้ชีพอย่างชัดเจน. มีกรณีหนึ่งที่ยืนยันได้ว่า ช่วงที่ผู้ป่วยรู้ตัวอยู่นั้น ไม่พบกิจกรรมหรือสัญญาณทางสมอง.
การที่มีการรู้ตัวในช่วงที่ไม่พบกิจกรรมทางสมอง อาจบอกได้ว่า (1) จิตไม่ได้ถูกสร้างจากสมอง หรือ (2) วิธีการวัดในปัจจุบันไม่สามารถวัดกิจกรรมที่เกี่ยวข้องนี้ได้. การอ้างการรู้ตัวในช่วงระหว่างการกู้ชีพได้ถูกตรวจสอบอย่างละเอียด. หนึ่งในการทดสอบก็คือ การทดสอบประสบการณ์ออกจากร่าง (out-of-body experience) ที่มักบรรยายถึง ความรู้สึกลอยออกจากร่างกายของตัวเอง และมองเห็นภาพต่าง ๆ จากมุมสูง. คณะของพาร์เนียเตรียมการทดสอบ โดยการติดตั้งหิ้งไว้ในห้องที่มีโอกาสสูงที่จะเกิดเหตุการณ์หัวใจวาย. บนหิ้ง จะวางรูปเอาไว้ โดยรูปหันหน้าขึ้นเพดาน ซึ่งผู้ที่อยู่ในห้องไม่สามารถที่จะมองเห็นภาพในรูป. ภาพในรูปจะใช้เพื่อพิสูจน์ความถูกต้องของคำบรรยายที่ได้จากประสบการณ์ออกจากร่าง. การทดสอบ พบว่า ผู้ที่อ้างประสบการณ์ออกจากร่างสามารถบรรยายภาพได้อย่างถูกต้อง. การบรรยายภาพในรูปได้ถูกต้อง บอกได้ว่า (1) การรับรู้สามารถแยกออกจากร่างกายได้ และ (2) ประสบการณ์ที่บรรยายเป็นประสบการณ์จริง ไม่ใช่ความฝัน จินตนาการ หรือผลของกิจกรรมที่สมองสร้างขึ้นมาเอง.
นอกจาก งานของพาร์เนียและคณะแล้ว ยังมีการศึกษาอื่น ๆ อีก ที่สนับสนุนสมมติฐานว่า (1) จิตไม่ได้เกิดจากสมอง และ (2) การรับรู้ของจิตสามารถแยกออกจากสมองได้. แม้ว่าจะมีหลักฐานสนับสนุนหนักแน่น แต่วงการจิตวิทยาและประสาทวิทยาส่วนใหญ่ ก็ยังเชื่อในแนวคิดเดิมอยู่ ส่วนหนึ่งก็เพราะว่า แม้หลักฐานจะบอกว่า จิตไม่ได้เกิดจากสมอง แต่ธรรมชาติของจิต การแยกออกจากสมอง ความสัมพันธ์กับสมอง ความสัมพันธ์กับชีวิต ชีวิตหลังความตาย กลไกที่อยู่เบื้องหลัง เงื่อนไขของประสบการณ์เฉียดตาย เรื่องเหล่านี้ วงการวิทยาศาสตร์ยังไม่รู้อะไรเลย. ปัจจุบันวงการวิชาการรู้เรื่องจิตน้อยมาก และหลาย ๆ อย่างที่คิดว่ารู้ ก็อาจจะไม่ถูกต้อง.
“We should not be ashamed to acknowledge truth from whatever source it comes to us, even if it is brought to us by former generations and foreign peoples. For him who seeks the truth there is nothing of higher value than truth itself.”
—Al-Kindi
“เราไม่ควรอายที่จะยอมรับความจริง ไม่ว่าเราได้รับมันมาจากไหน ถึงแม้ว่ามันจะมาจากคนรุ่นก่อนหรือมาจากคนต่างชาติ. สำหรับผู้แสวงหาความจริง ไม่มีอะไรมีค่ามากกว่าความจริง.”
—อัลคินดี
7.2.2.0.6 การกลับชาติมาเกิด
ในขณะที่ เรายังไม่เข้าใจความสัมพันธ์ของจิตและชีวิต สิ่งหนึ่งที่น่าสนใจ และอาจจะช่วยเติมภาพความสัมพันธ์นี้ให้ดีขึ้น คือ การศึกษาเรื่องการกลับชาติมาเกิด (reincarnation). ภาควิชาการศึกษาการรับรู้ มหาวิทยาลัยเวอร์จิเนีย (Division of Perceptual Studies, University of Virginia) ดำเนินการศึกษาเรื่องการกลับชาติมาเกิดมากว่า 50 ปี ซึ่งทัคเกอร์และคณะ ได้สรุปสาระสำคัญของผลจากการศึกษาว่า เด็กที่ระลึกชาติได้ มีมากกว่า 2,500 คนทั่วโลก เป็นเด็กอายุน้อยมาก ๆ (ไม่เกิน 6 ขวบ) พูดถึงชาติที่แล้ว ซึ่งเป็นชีวิตของคนธรรมดา ๆ ราวๆ 70% จะพูดถึงชาติที่แล้วที่ไม่ได้ตายตามธรรมชาติ เช่น ถูกฆ่าตาย หลาย ๆ คน มีอารมณ์หรือพฤติกรรม ที่สัมพันธ์กับคนในชาติที่แล้วที่อ้างถึง เด็กบางคนมีปานหรือตำหนิตั้งแต่เกิด ที่เข้ากับแผลของคนในชาติที่แล้วที่อ้าง เช่น มีเด็กอินเดียคนหนึ่งระลึกได้ว่า ชาติที่แล้ว เขาเกิดอุบัติเหตุ เครื่องจักรตัดนิ้วมือขวาเขาออกไป ตัวเด็กเองเกิดมา โดยไม่มีนิ้วมือขวา แต่มือซ้ายปกติ
เรื่องการกลับชาติมาเกิดไม่ได้เกี่ยวกับเชื้อชาติ หรือความเชื่อ เช่น กรณีของหนูน้อยเจมส์ ไลนินเกอร์ (James Leininger) ที่เป็นลูกชายของครอบครัวชาวคริสต์ที่หลุยส์เซียน่า สหรัฐอเมริกา เดิมครอบครัวไม่ได้เชื่อเรื่องการกลับชาติมาเกิดเลย. แต่ช่วงราว ๆ เจมส์อายุได้สองขวบ เจมส์ก็เริ่มมีฝันร้ายบ่อย ๆ. เจมส์ร้อง ดิ้น เตะขาในอากาศ “ไฟไหม้เครื่องบิน หนูน้อยออกไปไม่ได้” (“Airplane catches on fire. Little man can’t get out.”) เวลากลางวัน เจมส์เอาเครื่องบินมาเล่น แล้วก็เล่นทำเครื่องบินตก ทำแบบนั้นซ้ำ ๆ พอพ่อคุยกับเจมส์ เจมส์เล่าว่า เครื่องเขาถูกยิงตกโดยพวกญี่ปุ่น เจมส์ว่าเขาขับเครื่องคอร์แซร์ (Corsair). ตอนอายุ 28 เดือน เจมส์บอกว่าเขาบินออกจากเรือ พอพ่อถามถึงเรือ เจมส์บอกว่าเรือชื่อ นาโทม่า. ซึ่งช่วงสงครามโลกครั้งที่สอง ก็มีเรือรบยูเอสเอส นาโทม่า เบย์ (USS Natoma Bay) ที่ประจำการอยู่ในแปซิฟิก พอวาดรูป เจมส์ก็วาดแต่รูปเครื่องบินตก วาดเป็นสิบ ๆ รูป จนพ่อของเจมส์เริ่มคิดว่า หรือว่าเจมส์ระลึกชาติได้จริง ๆ
ตอนเจมส์อายุ 4 ขวบครึ่ง พ่อของเจมส์ไปร่วมงานสังสรรค์ทหารเกษียณของ ยูเอสเอส นาโทม่า เบย์ ถึงได้รู้ว่า มีนักบินคนเดียวในปฏิบัติการที่ถูกฆ่าตาย นักบินคนนั้นชื่อ เจมส์ ฮูสตัน (James Huston). เมื่อคณะนักวิจัยเปรียบเทียบ สิ่งที่หนูน้อยเจมส์พูดกับประวัติของฮูสตันก็พบว่า
| หนูน้อยเจมส์ ไลนินเกอร์ | เจมส์ ฮูสตัน |
|---|---|
| \(\bullet\) เซ็นต์ชื่อในรูปวาดว่า เจมส์ที่สาม (James 3) | \(\bullet\) เป็น เจมส์ จูเนียร์ (James, Jr.) |
| \(\bullet\) บอกว่าบินออกจากนาโทม่า | \(\bullet\) เป็นนักบินของ ยูเอสเอส นาโทม่า เบย์ |
| \(\bullet\) บอกว่าบินเครื่องคอร์แซร์ | \(\bullet\) เคยบินเครื่องคอร์แซร์ |
| \(\bullet\) บอกว่าถูกยิงตกโดยทหารญี่ปุ่น | \(\bullet\) ถูกยิงตกโดยทหารญี่ปุ่น |
| \(\bullet\) บอกว่าตายที่ฮิโรชิม่า | \(\bullet\) เป็นนักบินคนเดียวของ ยูเอสเอส นาโทม่า เบย์ ที่ถูกยิงตกตายในปฏิบัติการฮิโรชิม่า |
| \(\bullet\) บอก “เครื่องบินผมถูกยิงที่เครื่อง ตกลงน้ำ นั่นหละที่ผมตาย” | \(\bullet\) พยานที่เห็นเหตุการณ์รายงานว่า “ถูกยิงส่วนหน้าตรงกลางเครื่อง” |
| \(\bullet\) ฝันร้ายถึงเครื่องบินตกและจมน้ำบ่อย ๆ | \(\bullet\) เครื่องตกน้ำ และจมลงอย่างรวดเร็ว |
| \(\bullet\) บอกว่าเพื่อนผม แจ๊ค ลาร์เซน (Jack Larsen) อยู่ที่นั่นด้วย | \(\bullet\) แจ๊ค ลาร์เซน เป็นนักบินเครื่องที่อยู่ใกล้กับเครื่องของฮูสตัน วันที่ฮูสตันเครื่องตกตาย |
ในปี พ.ศ. 2560 หนูน้อยเจมส์ ไลนินเกอร์ อายุ 18 ปี เรียนจบมัธยมและได้เข้าทำงานกับกองทัพเรือ.
“Your assumptions are your windows on the world. Scrub them off every once in a while, or the light won’t come in.”
—Isaac Asimov
“ทิฐิเป็นเสมือนหน้าต่างที่มองโลกของคุณ ขัดมันออกบ้าง ไม่อย่างนั้นแสงมันจะไม่ส่องเข้ามา.”
—ไอแซค อาซิมอฟ
7.2.2.0.7 ประสบการณ์เฉียดตาย
นอกจากการกลับชาติมาเกิด ทัคเกอร์และคณะ ยังได้สรุปงานศึกษาประสบการณ์เฉียดตาย ที่ดำเนินการมาร่วม 40 ปี ของภาควิชาการศึกษาการรับรู้ ไว้ว่า ประสบการณ์เฉียดตาย พบได้ประมาณ 20% ในผู้ป่วยหัวใจวาย บรูซ เกรสัน (Bruce Grayson) หนึ่งในคณะได้เสนอแบบจำลอง ที่ใช้วัดความเข้มข้นของประสบการณ์เฉียดตาย จากสี่ส่วนประกอบ ได้แก่ (1) การเปลี่ยนกระบวนการความคิด, (2) การเปลี่ยนสถานะของอารมณ์ความรู้สึก, (3) ลักษณะเชิงปาฏิหารย์, และ (4) ลักษณะเชิงโลกอื่น.
การเปลี่ยนกระบวนการความคิด เช่น ความรู้สึกถึงการปราศจากเวลา (sense of timelessness), ความคิดที่รวดเร็วและชัดเจนกว่าปกติ, การทบทวนชีวิต (life review) ที่ผู้ป่วยรายงานว่า เห็นชีวิตที่ผ่านมาทั้งหมดฉายผ่านตา เหมือนกับเป็นสรุปของชีวิต, ความรู้สึกว่าเข้าใจ รู้สิ่งต่าง ๆ ชัดเจนแจ่มแจ้ง. การเปลี่ยนแปลงกระบวนการความรู้สึก เช่น ความรู้สึกถึงความสงบ ความพอใจ ความรู้สึกดี (sense of peace and well-being), รู้สึกมีความสุข (sense of joy), รู้สึกเป็นหนึ่งเดียว (sense of oneness or cosmic unity), รู้สึกถึงความรักและความอบอุ่น. ลักษณะของปาฏิหารย์ เช่น การมีชีวิตชีวาของสัมผัสต่างๆ ที่ผู้ป่วยรายงานว่า เห็นสีสันต่าง ๆ ที่ไม่เคยเห็นในโลกมาก่อน ได้ยินเสียงที่ไม่เคยได้ยินมาก่อน, การรับรู้ถึงเหตุการณ์ต่าง ๆ ที่เกิดขึ้น ระหว่างที่ผู้ป่วยหัวใจวาย, การรู้เห็นถึงอนาคต, การรู้สึกว่าได้ออกจากร่าง. ลักษณะของการสัมผัสโลกอื่น เช่น การได้เข้าไปในโลกอื่น, การได้พบกับสิ่งมีชีวิตที่ลึกลับ, การได้พบกับวิญญาณของคนที่ตายไปแล้ว, การได้พบกับจิตวิญญาณเชิงศาสนา, หรือว่า การได้ไปถึงจุดที่กลับไม่ได้ (a point of no return) ที่หากข้ามไปแล้ว จะกลับไม่ได้.
บรูซ เกรสัน บอกว่า ประสบการณ์เฉียดตายส่วนใหญ่จะมีลักษณะดังกล่าวผสม ๆ กัน โดยสัดส่วนแตกต่างกันไปตามแต่ละคน โดยได้ยกตัวอย่างประสบการณ์เฉียดตายของผู้หญิงคนหนึ่ง ที่เล่าว่า
“ในช่วงสงคราม ฉันนอนป่วยอยู่ในโรงพยาบาล. เช้าวันหนึ่ง นางพยาบาลเข้ามา และพบว่าฉันไม่มีสัญญาณชีพใด ๆ เลย. นางพยาบาลตามหมอมา ซึ่งหมอก็พบว่าฉันตายแล้วเช่นกัน และฉันก็ตายอยู่อย่างนั้นราวๆ 20 นาที ตามที่หมอบอกฉันในภายหลัง.
ฉันรับรู้แสงสว่างแพรวพราว ที่ฉันรู้สึกถูกเย้ายวนตามมันไป. ตอนนั้นเหมือนกับว่า เวลามันแตกต่างออกไป เหมือนมันไม่มีเวลาอยู่ที่นั่น ไม่ว่าที่นั่น มันจะคือที่ไหน. แสงนั้นสวยงามมาก และมันก็ให้ความรู้สึกของความรักที่ปราศจากเงื่อนไข (unconditional love) และความสงบสุข. เมื่อมองไปรอบๆ ฉันก็พบว่า ฉันอยู่ในที่ที่สวยงาม เขียว เป็นเนินขึ้นลง. แล้วฉันก็เห็นนายทหารหนุ่มกับทหารอีกหลายนายเดินเข้ามา. นายทหารหนุ่มเป็น อัลบิน ญาติคนโปรดของฉัน. ตอนนั้น ฉันไม่รู้ว่าอัลบินตายแล้ว และฉันก็ไม่เคยเห็นอัลบินในชุดเครื่องแบบมาก่อนด้วย. แต่ว่าสิ่งที่ฉันเห็น ก็ยืนยันได้จากภาพถ่ายที่ฉันได้เห็นหลายปีหลังจากนั้น. ฉันคุยกับอัลบินอย่างมีความสุขอยู่สักพัก แล้วอัลบินกับเพื่อนทหารก็เดินแถวออกไป. แล้วคนข้าง ๆ ฉันก็อธิบายว่า ทหารเหล่านี้ได้รับอนุญาตให้ไปทักทายคนอื่น ๆ ที่เพิ่งตาย และช่วยแนะนำเขากับความตาย. ความทรงจำที่มีชีวิตชีวาต่อมา ก็คือการมองจากความสูงประมาณเพดานลงไปที่เตียง บนเตียง มีร่างซูบผอมนอนอยู่. มีหมอและพยาบาลอยู่รอบ ๆ เตียง. ฉันตะโกนเรียก แต่ไม่มีใครได้ยินฉัน. ฉันเห็นทุกอย่างอย่างชัดเจน และรู้สึกอบอุ่น ปลอดภัย และสุขสงบ.
อึดใจต่อมา ฉันมองขึ้นไปเห็นหมอกับพยาบาลเหล่านั้น และก็รู้สึกผิดหวังอย่างแรง. ฉันพึ่งออกมาจากสิ่งที่น่าเบิกบานใจ น่าพอใจอย่างที่สุด. สองวันหลังจากนั้น หมอเข้ามาคุยกับฉันว่า ฉันโชคดีที่ยังไม่ตาย. ฉันตอบหมอไปว่า ฉันตายไปแล้ว. หมอมองฉันแบบแปลกๆ แล้วก็นัดให้ฉันไปประเมินสภาพจิต. และฉันก็ได้เรียนรู้ที่จะหุบปากเรื่องนี้ ตั้งแต่นั้นเป็นต้นมา.”
เกรสันอภิปรายว่า อิทธิพลของความเชื่อและวัฒนธรรมไม่ได้มีผลต่อประสบการณ์เฉียดตาย แต่ความเชื่อและวัฒนธรรมมีอิทธิพลต่อการตีความของประสบการณ์เฉียดตาย เช่น ผู้ผ่านประสบการณ์เฉียดตายในโลกที่สามจะบรรยายถึง ถ้ำ หรือบ่อน้ำ แทนอุโมงค์ ที่ผู้ผ่านประสบการณ์เฉียดตายในอเมริกาบรรยาย.
คณะผู้วิจัยได้ทำการศึกษาและยืนยันถึงความน่าเชื่อถือของความทรงจำ ในประสบการณ์เฉียดตายที่คงเส้นคงวา แม้ว่าจะเปรียบเทียบการให้สัมภาษณ์ถึงประสบการณ์เฉียดตาย ที่คณะผู้วิจัยกลับไปสัมภาษณ์หลังการสัมภาษณ์เดิมที่เวลาต่างกันร่วม 10 ถึง 20 ปี. และ เพื่อตอบคำถามว่าความทรงจำในประสบการณ์เฉียดตาย เป็นความทรงจำของเหตุการณ์จริงๆ ไม่ใช่แค่ความทรงจำของจินตนาการ หรือจากภาพหลอน คณะผู้วิจัยใช้แบบสอบถามลักษณะพิเศษของความทรงจำ (memory characteristics questionnaire) ที่ออกแบบมาเพื่อจำแนกแยก ความทรงจำของเหตุการณ์จริง ออกจากความทรงจำของเหตุการณ์ในจินตนาการ.
แบบสอบถามลักษณะพิเศษของความทรงจำ ทดสอบความทรงจำใน 5 แง่มุม ซึ่งสามารถแยกความทรงจำของเหตุการณ์จริง ออกจากเหตุการณ์สมมติ หรือเหตุการณ์ในจินตนาการได้อย่างน่าเชื่อถือ. แง่มุมต่างๆ ได้แก่ แง่ความชัดเจนของความทรงจำ (clarity of memories) ซึ่งรวมถึง รายละเอียดของสิ่งที่เห็น, แง่การรับสัมผัส (sensory aspects) เช่น เสียง กลิ่น รส, แง่ของบริบท (contextual features) เช่น ความทรงจำเกี่ยวกับตำแหน่ง และ การจัดเรียงเชิงพื้นที่ (spatial arrangements), แง่ความคิดและความรู้สึก (thoughts and feelings) ระหว่างที่ระลึกถึงเหตุการณ์, และแง่ความเข้มข้นของความรู้สึก (intensity of feeling) ระหว่างเหตุการณ์และขณะรำลึกถึง.
คณะผู้วิจัยประเมินผู้ผ่านประสบการณ์เฉียดตาย สำหรับเหตุการณ์ประสบการณ์เฉียดตาย เหตุการณ์จริงอื่นที่เกิดขึ้นในชีวิตในเวลาใกล้เคียงกัน และเหตุการณ์ในจินตนาการที่เกิดขึ้นในช่วงเวลานั้น. การทดสอบพบว่า ผู้ผ่านประสบการณ์เฉียดตายจำประสบการณ์เฉียดตาย ได้ชัดเจน ละเอียด มีบริบท และด้วยความเข้มข้นของความรู้สึก ที่มากกว่า เหตุการณ์จริงอื่นที่เกิดในช่วงเวลาใกล้เคียงกัน. ประสบการณ์เฉียดตายถูกระลึกถึงว่า จริงกว่าเหตุการณ์จริง ในระดับขั้นเดียวกับ ที่เหตุการณ์จริง จริงกว่าเหตุการณ์ในจินตนาการ. ในขณะที่ผู้ที่ไม่ได้มีประสบการณ์เฉียดตาย แต่ผ่านเหตุการณ์กู้ชีพในลักษณะคล้ายกัน จะรายงานความทรงจำช่วงเหตุการณ์ชีวิตนั้น ว่าจริงในระดับขั้นเดียวกันกับเหตุการณ์จริงอื่น ๆ เท่านั้น ไม่ได้พบว่าจริงมากกว่า.
เกรสันและคณะยังไม่พบปัจจัยใดที่จะสามารถทำนายถึงผู้ที่จะมีประสบการณ์เฉียดตายได้ ไม่ว่าจะเป็นปัจจัย อายุ เชื้อชาติ เพศ ศาสนา ความเคร่งศาสนา หรืออาการป่วยทางจิต และได้ให้ข้อสังเกตว่า แม้จะมีแนวคิดที่พยายามเชื่อมโยง สภาวะทางสรีรวิทยา ทางกายภาพ ทางชีวภาพ เข้ากับประสบการณ์เฉียดตาย แต่ที่สุดแล้ว มันก็ยากที่จะอธิบายถึง ความสามารถของสมองที่เพิ่มขึ้น การคิดและรับรู้ได้ชัดเจนขึ้น ในขณะที่สมองไม่สมบูรณ์ ไม่ว่าจากยาสลบ หรือจากภาวะหัวใจวาย.
แม้ว่าประสบการณ์เฉียดตาย อาจเป็นเงื่อนงำของการแยกกันระหว่างจิตกับสมอง หรืออาจเป็นหลักฐานสำคัญของชีวิตหลัง แต่สิ่งที่น่าสนใจที่สุดเกี่ยวกับประสบการณ์เฉียดตาย ก็คือ ผลจากการผ่านประสบการณ์เฉียดตาย. ผู้ที่ผ่านประสบการณ์เฉียดตายจะมีการเปลี่ยนแปลงในเชิงความเชื่อ ทัศนคติ ค่านิยม ได้แก่ มีความเชื่อและศรัทธาในเรื่องของจิตวิญญาณมากขึ้น (increase in spirituality), มีความเป็นห่วงเป็นใยมีเมตตาต่อผู้อื่นมากขึ้น (increase in sense of concern/compassion for others), ตระหนักในค่าของชีวิตมากขึ้น (increase in appreciation of life), ใช้ชีวิตมีคุณค่า มีความหมายมากขึ้น (increase in sense of meaning or purpose), มีความมั่นใจ มีความยืดหยุ่นในทักษะการรับมือกับสถาณการณ์ต่าง ๆ ได้ดีขึ้น (increase in confidence and flexibility in coping skills), และเชื่อในชีวิตหลังความตาย (a belief in postmortem survival). ในขณะเดียวกัน ผู้ผ่านประสบการณ์เฉียดตาย จะลดการกลัวตายลง (decrease in fear of death), มีความสนใจในวัตถุนิยมลดลง (decreased interest in material possession), ลดความสนใจในสถานะ อำนาจ เกียรติ และชื่อเสียงลง (decreased interest in status, power, prestige, and fame), ลดความสนใจในการแก่งแย่งชิงดีชิงเด่นลง (decreased interest in competition).
ถึงตรงนี้ อาจทำให้เกิดคำถามว่า ถ้าผู้ผ่านประสบการณ์เฉียดตายไม่กลัวตาย และพบว่าความตายนั้นเป็นสุขและสวยงาม ทำไมเขาไม่ฆ่าตัวตายไปเลย แต่กลับรักและชื่นชมคุณค่าของชีวิต และใช้ชีวิตอย่างมีความหมาย. คำถามนี้ ทัคเกอร์ เกรสัน และคณะไม่ได้อภิปรายไว้. แต่หากลองใคร่ครวญพิจารณาด้วยตนเองแล้ว จะพบว่าชีวิตคนนั้นแปลก. คนที่เห็นความตาย กลับไม่กลัวตาย. คนที่กลัวตาย ไม่เคยเห็นความตาย. คนไม่กลัวความตาย กลับเข้าใจชีวิต ใช้ชีวิตได้ดี ใช้ชีวิตอย่างมีคุณค่า. แต่คนทั่วไปที่ส่วนใหญ่กลัวความตาย หลายคนเลือกใช้ชีวิตทิ้งเปล่าไป. หลายคนเลือกเล่นโทรศัพท์มือถือ แทนการมีปฏิสัมพันธ์กับคนรอบข้าง. หลายคนเลือกใช้ชีวิตเห็นแก่ตัว เลือกเป้าหมายชีวิตเป็นความร่ำรวย สถานะ ชื่อเสียง ตอบสนองต่ออัตตาที่ขยายไม่รู้จบ แล้วเรียกมันว่า ความสำเร็จ. หลายคนทิ้งคุณค่าของชีวิต ทิ้งความสงบสุข เพื่อใช้ชีวิตที่ฟุ้งเฟ้อ. หลายคนทิ้งความกล้าที่จะทำในสิ่งที่ถูกต้อง ทิ้งความซื่อสัตย์มั่นคงที่จะยืนหยัดในหลักการที่อ้าง ทิ้งเมตตา ทิ้งปัญญา อันเป็นคุณธรรมอันสูงสุด ทั้งโดยรู้ตัวและไม่รู้ตัว. หลายคนกลัวความตาย แต่กลับไม่เคยใช้ชีวิตให้มีคุณค่าเลย. ประเด็นนี้ก็เป็นอีกปริศนาของชีวิตที่ยากจะอธิบาย และข้อสังเกตนี้ก็ได้ถูกกล่าวไว้อย่างงดงามโดยท่านดาไลลามาองค์ที่สิบสี่ แห่งธิเบตดังนี้.
“[What surprises me most is] Man. Because he sacrifices his health in order to make money. Then he sacrifices money to recuperate his health. And then he is so anxious about the future that he does not enjoy the present; the result being that he does not live in the present or the future; he lives as if he is never going to die, and then dies having never really lived.”
—Tenzin Gyatso, the 14th Dalai Lama
“[สิ่งที่ทำให้อาตมาแปลกใจที่สุดคือ] คน. เพราะว่า คนสละสุขภาพไปเพื่อหาเงิน แล้วทีหลังก็สละเงินไปเพื่อฟื้นฟูสุขภาพ และคนก็มัวแต่กังวลกับอนาคต จนไม่มีความสุขกับปัจจุบัน ผลก็คือเขาไม่ได้อยู่ในปัจจุบันไม่ได้อยู่ในอนาคต เขาใช้ชีวิตอยู่เหมือนกับว่าเขาจะไม่มีวันตาย แล้วก็ตายไปแบบไม่เคยมีชีวิตจริง ๆ.”
—เทนซิน กิยันโซ่, ดาไลลามาที่สิบสี่
7.3 อภิธานศัพท์
- การตรวจับวัตถุในภาพ (object detection):
ภาระกิจการระบุชนิดของวัตถุและตำแหน่งในภาพ
- โยโล่ (YOLO):
แบบจำลองที่สำคัญในการตรวจับวัตถุในภาพ ซึ่งมีแนวคิดที่สำคัญคือวางกรอบปัญหาเป็นงานการหาค่าถดถอย และช่วยลดขั้นตอนการทำงานที่ซับซ้อนลงได้ ส่งผลให้แบบจำลองสามารถทำงานได้รวดเร็ว และการแก้ไขปรับปรุงก็ทำได้สะดวก
- กล่องสมอ (anchor box):
เทคนิคที่ยอมให้มีการทายวัตถุในภาพที่มีตำแหน่งซ้อนทับกันได้ โดยใช้กลไกของรูปร่างและขนาดเริ่มต้นที่ต่างกันของกล่องขอบเขต เพื่อกำหนดความรับผิดชอบต่อวัตถุ คล้ายการปักสมอของแต่ละกล่องขอบเขต ว่ากล่องใดจะรับผิดชอบขนาดหรือรูปทรงคร่าว ๆ แบบใด
- โครงข่ายปรปักษ์เชิงสร้าง (Generative Adversarial Networks คำย่อ GANs):
กลไกการฝึกโครงข่ายสองโครงข่าย โดยฝึกในลักษณะที่ทั้งสองโครงข่ายมีเป้าหมายขัดแย้งกัน. โครงข่ายหนึ่ง เรียกว่า โครงข่ายก่อกำเนิด ทำหน้าที่สร้างจุดข้อมูลขึ้นมา เลียนแบบจุดข้อมูลจริง ในขณะที่อีกโครงข่ายหนึ่ง เรียกว่า โครงข่ายแบ่งแยก ทำหน้าที่ตรวจสอบ ว่าจุดข้อมูลที่เห็นถูกสุ่มจากชุดข้อมูลจริง หรือถูกสร้างขึ้น. โครงข่ายก่อกำเนิด มีเป้าหมายเป็นการสร้างจุดข้อมูลเลียนแบบให้เหมือนข้อมูลจริง จนโครงข่ายแบ่งแยกจำแนกไม่ออก. โครงข่ายแบ่งแยก มีเป้าหมายเป็นการจำแนกจุดข้อมูลได้ถูกต้องมากที่สุด
- โครงข่ายแบ่งแยก (discriminator):
โครงข่ายหนึ่งในกลไกการฝึกแบบปรปักษ์ ทำหน้าที่จำแนกจุดข้อมูลที่เห็นว่า ถูกสุ่มจากชุดข้อมูลจริง หรือถูกสร้างขึ้น
- โครงข่ายก่อกำเนิด (generator):
โครงข่ายหนึ่งในกลไกการฝึกแบบปรปักษ์ ทำหน้าที่สร้างจุดข้อมูลเลียนแบบจุดข้อมูลจริงจนโครงข่ายแบ่งแยกจำแนกได้แย่ที่สุด
- พีชคณิตเวกเตอร์ (Vector arithmetic):
สำหรับโครงข่ายปรปักษ์เชิงสร้าง พีชคณิตเวกเตอร์ อ้างถึง ปฏิบัติการเชิงเส้นที่ทำกับเวกเตอร์ลักษณะซ่อนเร้น แล้วนำเวกเตอร์ผลลัพธ์ไปเข้าโครงข่ายก่อกำเนิด เพื่อสร้างจุดข้อมูลขึ้นมา
- ลักษณะซ่อนเร้น (latent representation):
ลักษณะของข้อมูล ที่ไม่ได้แสดง หรือกำหนดอย่างชัดแจ้ง. ในบริบทของโครงข่ายปรปักษ์เชิงสร้าง หมายถึง ค่าของเวกเตอร์ที่ใช้เป็นอินพุตของโครงข่ายก่อกำเนิด
- ปริภูมิซ่อนเร้น (latent space):
หรือปริภูมิตัวแทน (representation space) ปริภูมิของลักษณะซ่อนเร้น
- การพังทลายของภาวะ (mode collapse):
สถานการณ์ที่โครงข่ายก่อกำเนิดสร้างจุดข้อมูลคล้าย ๆ กัน แม้ว่าจะรับอินพุตที่ต่างกัน
- คอนโวลูชั่นก้าวเศษ (fractionally-strided convolution):
หรือคอนโวลูชั่นสลับเปลี่ยน (transposed convolution) การดำเนินคอนโวลูชั่นด้วยการแปลงอินพุตและค่าน้ำหนักของฟิลเตอร์เป็นเมทริกซ์ โดยจัดรูปเมทริกซ์ทั้งสองให้ถูกต้อง แล้วทำการคูณเมทริกซ์อินพุตเข้ากับการสลับเปลี่ยนของเมทริกซ์ค่าน้ำหนัก. หากเลือกอภิมานพารามิเตอร์ได้ถูกต้อง การดำเนินการเช่นนี้ อาจมองเสมือนเป็นการทำคอนโวลูชั่นที่ใช้ขนาดก้าวย่างเล็กกว่าหนึ่ง (เหมือนการเติมพิกเซลค่าศูนย์เข้าไประหว่างพิกเซลของอินพุต ในกรณีข้อมูลภาพ)
- การถอดคอนโวลูชั่น (deconvolution):
การถอดคอนโวลูชั่น มีหลายความหมาย. ในขณะที่บางครั้ง การถอดคอนโวลูชั่นอาจหมายถึงคอนโวลูชั่นก้าวเศษ แต่ความหมายที่ถูกยอมรับอย่างกว้างขวาง คือการถอดค่าพารามิเตอร์ของโครงข่ายคอนโวลูชั่นย้อนกลับ เพื่อศึกษากลไกการทำงานของโครงข่ายคอนโวลูชั่น ว่า ฟิลเตอร์แต่ละตัวที่ใช้ในโครงข่ายคอนโวลูชั่น ได้เรียนรู้เพื่อจะตรวจจับลักษณะรูปแบบเช่นไร
- การจับคู่ลักษณะสำคัญ (feature matching):
ในบริบทของโครงข่ายปรปักษ์เชิงสร้าง การจับคู่ลักษณะสำคัญ หมายถึงการดัดแปลงฟังก์ชันจุดประสงค์ของโครงข่ายก่อกำเนิด โดย แทนที่เป้าหมายการทำให้โครงข่ายแบ่งแยกทายผิดมากที่สุด ด้วยเป้าหมายการทำให้ความต่างระหว่าง ค่าเฉลี่ยของลักษณะสำคัญภายในโครงข่ายแบ่งแยก เมื่อเห็นจุดข้อมูลจริง กับค่าเฉลี่ยของลักษณะสำคัญเมื่อเห็นจุดข้อมูลที่สร้างขึ้น มีค่าน้อยที่สุด. ตัวอย่างเช่น การใช้ฟังก์ชันสูญเสีย \(\mathrm{Loss}_{\mathcal{G}} = \| E_{\boldsymbol{X}}[ \boldsymbol{f}(\boldsymbol{X})] - E_{\boldsymbol{z}}[ \boldsymbol{f}(\mathcal{G}(\boldsymbol{z}))]\|^2\) เมื่อ \(\boldsymbol{X}\) คือข้อมูลจริง และ \(\boldsymbol{z}\) แทนเวกเตอร์ค่าสุ่ม ส่วน \(\mathcal{G}(\cdot)\) คือการคำนวณของโครงข่ายก่อกำเนิด และ \(\boldsymbol{f}(\cdot)\) คือลักษณะสำคัญที่ได้จากโครงข่ายแบ่งแยก
- การแยกแยะหมู่เล็ก (minibatch discrimination):
การเพิ่มสัญญาณข้อมูลที่บอกความแตกต่างระหว่างจุดข้อมูลใด ๆ กับจุดข้อมูลอื่น ๆ ภายในหมู่เล็กเดียวกัน เพื่อลดบรรเทาปัญหาการพังทลายของภาวะ
- การทำฉลากราบรื่น (label smoothing):
การปรับค่าเป้าหมายของฉลากเฉลย เพื่อบรรเทาปัญหาที่แบบจำลองมีความมั่นใจสูงเกินไป
- การทำหมู่เล็กเสมือนจริง (virtual minibatch):
การใช้หมู่อ้างอิงที่เลือกมาก่อนกระบวนการฝึก เพื่อใช้การคำนวณแบชนอร์ม ร่วมกับจุดข้อมูลที่สนใจ