6 แบบฝึกหัด
“Success is not final, failure is not fatal, it is the courage to continue that counts.”
—Winston Churchill
“ความสำเร็จไม่ใช่สิ้นสุด ความล้มเหลวไม่ใช่จุดจบ มีเพียงความกล้าหาญที่ไปต่อเท่านั้นที่สำคัญ.”
—วินสตัน เชอร์ชิล
6.0.0.0.1 แบบฝึกหัด
จงตอบคำถามต่อไปนี้ เกี่ยวกับชั้นคอนโวลูชั่น ลำดับชั้น และชุดมิติต่าง ๆ
(ก) อินพุตเป็นเวกเตอร์ นั่นคือ \(\boldsymbol{x} \in \mathbb{R}^{10}\) และชั้นคอนโวลูชั่นใช้ฟิลเตอร์ \(\boldsymbol{w}\) มีขนาด \(3\) จำนวน \(15\) ตัว โดยไม่มีการเติมเต็ม ขนาดย่างก้าวเป็น \(1\) แล้วผลลัพธ์จากชั้นคอนโวลูชั่น จะเป็นเทนเซอร์ขนาดเท่าใด? คำใบ้ ดูสมการ \(\eqref{eq: deep conv filter x of D}\) (สำหรับฟิลเตอร์แต่ละตัว เอาต์พุต \(a_k = b + \sum_j w_j \cdot x_{k+j-1}\) โดย \(k = 1, \ldots, H - H_F + 1\)). สังเกต รูปแบบของเทนเซอร์ที่ใช้ คือ ชุดมิติแรกเป็นจำนวนลักษณะสำคัญ และตามด้วยชุดมิติอื่น ๆ (เช่น ชุดมิติลำดับ).
(ข) อินพุตเป็นเทนเซอร์สองลำดับชั้น คือ \(\boldsymbol{X} \in \mathbb{R}^{8 \times 10}\). ชั้นคอนโวลูชั่นใช้ฟิลเตอร์ \(\boldsymbol{W}\) ขนาด \(8 \times 3\) จำนวน \(15\) ตัว โดยทำคอนโวลูชั่น (การเชื่อมต่อท้องถิ่นและใช้ค่าน้ำหนักร่วม) เฉพาะกับชุดมิติที่สอง (ชุดมิติแรกเป็นเสมือนช่องลักษณะสำคัญที่ไม่มีความสัมพันธ์ในเชิงลำดับ). ไม่มีการเติมเต็มอินพุต และใช้ขนาดย่างก้าวเป็น \(1\). ผลลัพธ์จากชั้นคอนโวลูชั่น จะเป็นเทนเซอร์ขนาดเท่าใด? คำใบ้ สำหรับฟิลเตอร์แต่ละตัว เอาต์พุต \(a_k = b + \sum_c \sum_j w_{c, j} \cdot x_{c, k+j-1}\) โดย \(c\) แทนดัชนีของช่องลักษณะสำคัญ (ไม่มีความสัมพันธ์ในเชิงลำดับ) และ \(k = 1, \ldots, H - H_F + 1\).
(ค) อินพุตเป็นเทนเซอร์สามลำดับชั้น นั่นคือ \(\boldsymbol{X} \in \mathbb{R}^{3 \times 100 \times 200}\). ชั้นคอนโวลูชั่นใช้ฟิลเตอร์ \(\boldsymbol{W}\) ขนาด \(3 \times 5 \times 5\) จำนวน \(24\) ตัว โดยทำคอนโวลูชั่น (การเชื่อมต่อท้องถิ่นและใช้ค่าน้ำหนักร่วม) เฉพาะกับชุดมิติที่สองและสาม (ชุดมิติแรกเป็นเสมือนช่องลักษณะสำคัญที่ไม่มีความสัมพันธ์ในเชิงลำดับ). ไม่มีการเติมเต็มอินพุต และใช้ขนาดย่างก้าวเป็น \(1\). ผลลัพธ์จากชั้นคอนโวลูชั่น จะเป็นเทนเซอร์ขนาดเท่าใด? คำใบ้ ดูสมการ \(\eqref{eq: deep conv conv CxHxW}\) (สำหรับฟิลเตอร์แต่ละตัว เมื่อขนาดก้าวย่างเป็นหนึ่ง เอาต์พุต \(a_{k,l} = b + \sum_{c} \sum_{i} \sum_{j} w_{c,i,j} \cdot x_{c, k+i-1, l+j-1}\) ).
(ง) อินพุตเป็นเทนเซอร์สี่ลำดับชั้น นั่นคือ \(\boldsymbol{X} \in \mathbb{R}^{4 \times 300 \times 400 \times 50}\). ชั้นคอนโวลูชั่นใช้ฟิลเตอร์ \(\boldsymbol{W}\) ขนาด \(4 \times 11 \times 11 \times 7\) จำนวน \(64\) ตัว โดยทำคอนโวลูชั่น (การเชื่อมต่อท้องถิ่นและใช้ค่าน้ำหนักร่วม) เฉพาะกับชุดมิติที่สอง ที่สาม และที่สี่ (ชุดมิติแรกเป็นเสมือนช่องลักษณะสำคัญที่ไม่มีความสัมพันธ์ในเชิงลำดับ). ไม่มีการเติมเต็มอินพุต และใช้ขนาดย่างก้าวเป็น \(1\). ผลลัพธ์จากชั้นคอนโวลูชั่น จะเป็นเทนเซอร์ขนาดเท่าใด? คำใบ้ สำหรับฟิลเตอร์แต่ละตัว เอาต์พุต \(a_{k,l,m} = b + \sum_{c} \sum_{i} \sum_{j} \sum_{q} w_{c,i,j,q} \cdot x_{c, k+i-1, l+j-1, m+q-1}\).
6.0.0.0.2 แบบฝึกหัด
จากแบบฝึกหัด 1.0.0.0.1 จงประมาณขนาดเทนเซอร์ของเอาต์พุต ในกรณีต่าง ๆ เมื่อใช้ขนาดย่างก้าวเป็น \(2\), เป็น \(3\) และเป็น \(4\). คำใบ้ ดูสมการ \(\eqref{eq: deep size of conv output}\) ( \(H' = \left\lfloor \frac{H - H_F}{S} \right\rfloor + 1\) ).
6.0.0.0.3 แบบฝึกหัด
จากแบบฝึกหัด 1.0.0.0.1 จงประมาณการเติมเต็มด้วยค่าศูนย์ (จำนวนค่าศูนย์ที่ต้องเติม) ทั้ง \(4\) กรณี โดย
(แบบที่ 1) เติมให้เอาต์พุตมีขนาดเท่ากับอินพุต เมื่อใช้ขนาดก้าวย่างเป็น \(1\) (พิจารณาเฉพาะในชุดมิติที่มีความสัมพันธ์เชิงลำดับ เช่น กรณี ข อินพุต \(\boldsymbol{X} \in \mathbb{R}^{8 \times 10}\) แต่ชุดมิติแรกไม่มีความสัมพันธ์เชิงลำดับ. ดังนั้น สัดส่วนของเอาต์พุตที่ต้องการคือ \(15 \times 10\) หรือเอาต์พุต \(\boldsymbol{A} \in \mathbb{R}^{15 \times 10}\). ขนาด \(15\) มาจากจำนวนฟิลเตอร์ที่ใช้ ไม่เกี่ยวกับการเติมเต็มด้วยค่าศูนย์).
(แบบที่ 2) เติมให้เอาต์พุตมีขนาดเท่ากับ \(\left\lceil\frac{H}{S}\right\rceil\) โดย \(H\) คือขนาดอินพุต และ \(S\) คือขนาดก้าวย่าง เมื่อใช้ขนาดก้าวย่างเป็น \(2\), เป็น \(3\), และเป็น \(4\) ตามลำดับ. (พิจารณาเฉพาะในชุดมิติที่มีความสัมพันธ์เชิงลำดับ เช่น กรณี ค อินพุต \(\boldsymbol{X} \in \mathbb{R}^{3 \times 100 \times 200}\) แต่ชุดมิติแรกไม่มีความสัมพันธ์เชิงลำดับ. ดังนั้น สัดส่วนของเอาต์พุตที่ต้องการคือ \(24 \times 50 \times 100\) เมื่อใช้ขนาดก้าวย่าง \(2\) และคือ \(24 \times 34 \times 67\) เมื่อใช้ขนาดก้าวย่าง \(3\) เป็นต้น).
คำใบ้ ดูสมการ \(\eqref{eq: deep size of padded input}\) ซึ่งคือ \(\hat{H} = S \cdot (\hat{H}' - 1) + H_F\) และ \(\hat{H} - H\).
6.0.0.0.4 แบบฝึกหัด
จงคำนวณขนาดของเอาต์พุตจากชั้นคอนโวลูชั่น สำหรับกรณีต่าง ๆ ดังนี้
(ก) อินพุตเป็นเวกเตอร์ นั่นคือ \(\boldsymbol{x} \in \mathbb{R}^{10}\) และชั้นคอนโวลูชั่นใช้ฟิลเตอร์ \(\boldsymbol{w}\) มีขนาด \(3\) จำนวน \(15\) ตัว โดยเติมเต็มด้วยค่าศูนย์จำนวนรวม \(2\) ตัว ขนาดย่างก้าวเป็น \(1\) แล้วผลลัพธ์จากชั้นคอนโวลูชั่น จะเป็นเทนเซอร์ขนาดเท่าใด?
(ข) อินพุตเป็นเทนเซอร์สองลำดับชั้น คือ \(\boldsymbol{X} \in \mathbb{R}^{8 \times 10}\). ชั้นคอนโวลูชั่นใช้ฟิลเตอร์ \(\boldsymbol{W}\) ขนาด \(8 \times 3\) จำนวน \(15\) ตัว โดยทำคอนโวลูชั่น (การเชื่อมต่อท้องถิ่นและใช้ค่าน้ำหนักร่วม) เฉพาะกับชุดมิติที่สอง (ชุดมิติแรกเป็นเสมือนช่องลักษณะสำคัญที่ไม่มีความสัมพันธ์ในเชิงลำดับ). มีการเติมเต็มอินพุตด้วยค่าศูนย์จำนวน \(7\) ตัว และใช้ขนาดย่างก้าวเป็น \(2\). ผลลัพธ์จากชั้นคอนโวลูชั่น จะเป็นเทนเซอร์ขนาดเท่าใด?
(ค) อินพุตเป็นเทนเซอร์สามลำดับชั้น นั่นคือ \(\boldsymbol{X} \in \mathbb{R}^{3 \times 100 \times 200}\). ชั้นคอนโวลูชั่นใช้ฟิลเตอร์ \(\boldsymbol{W}\) ขนาด \(3 \times 5 \times 5\) จำนวน \(24\) ตัว โดยทำคอนโวลูชั่น (การเชื่อมต่อท้องถิ่นและใช้ค่าน้ำหนักร่วม) เฉพาะกับชุดมิติที่สองและสาม (ชุดมิติแรกเป็นเสมือนช่องลักษณะสำคัญที่ไม่มีความสัมพันธ์ในเชิงลำดับ). มีการเติมเต็มอินพุตด้วยค่าศูนย์จำนวน \(11\) ตัวในแต่ละชุดมิติ (ยกเว้นชุดมิติแรก) และใช้ขนาดย่างก้าวเป็น \(3\). ผลลัพธ์จากชั้นคอนโวลูชั่น จะเป็นเทนเซอร์ขนาดเท่าใด?
คำใบ้ \(H' = \left\lfloor \frac{H - H_F + P}{S} \right\rfloor + 1\) เมื่อ \(P\) คือจำนวนศูนย์ที่เติมเข้าไปทั้งหมด.
6.0.0.0.5 แบบฝึกหัด
จงคำนวณขนาดของสนามรับรู้ของหน่วยย่อยในชั้นสุดท้ายของกรณีต่อไปนี้
(ก) โครงข่ายคอนโวลูชั่นหนึ่งชัั้น ที่ใช้ฟิลเตอร์ขนาด \(5 \times 5\) ขนาดก้าวย่างเป็น \(1 \times 1\), เป็น \(2 \times 2\) และเป็น \(3 \times 3\) ตามลำดับ.
(ข) โครงข่ายคอนโวลูชั่นสองชัั้น ทั้งสองชั้นใช้ฟิลเตอร์ขนาด \(5 \times 5\) ขนาดก้าวย่างเป็น \(1 \times 1\).
(ค) โครงข่ายคอนโวลูชั่นสองชัั้น ทั้งสองชั้นใช้ฟิลเตอร์ขนาด \(11 \times 11\) ขนาดก้าวย่างเป็น \(1 \times 1\).
(ง) โครงข่ายคอนโวลูชั่นสามชัั้น ทั้งสองชั้นใช้ฟิลเตอร์ขนาด \(5 \times 5\) ขนาดก้าวย่างเป็น \(1 \times 1\).
(จ) โครงข่ายคอนโวลูชั่นห้าชั้น โดยฟิลเตอร์ชั้นแรก \(11 \times 11\) ก้าวย่าง \(1 \times 1\), ฟิลเตอร์ชั้นสอง \(5 \times 5\) ก้าวย่าง \(1 \times 1\), ฟิลเตอร์ชั้นสามถึงห้าใช้ฟิลเตอร์แบบเดียวกัน คือ \(3 \times 3\) ก้าวย่าง \(1 \times 1\).
(ฉ) โครงข่ายคอนโวลูชั่นสิบชั้น โดยทุกชั้นใช้ฟิลเตอร์แบบเดียวกัน คือ \(3 \times 3\) ก้าวย่าง \(1 \times 1\).
(ช) โครงข่ายคอนโวลูชั่นสามชัั้น ชั้นที่หนึ่งและสามใช้ฟิลเตอร์ขนาด \(3 \times 3\) ขนาดก้าวย่างเป็น \(1 \times 1\) แต่ชั้นที่สองใช้ฟิลเตอร์ขนาด \(2 \times 2\) ก้าวย่าง \(2 \times 2\).
คำใบ้ ดูสมการ \(\eqref{eq: receptive field}\) (\(R_k = 1 + \sum_{j=1}^k (F_j - 1) \prod_{i=0}^{j-1} S_i\) และกำหนด \(S_0 = 1\))
6.0.0.0.6 แบบฝึกหัด
จากสมการ \(\eqref{eq: deep conv conv FxCxHxW}\) และ \(\eqref{eq: deep conv 2Dconv Output}\) สำหรับคอนโวลูชั่นสองมิติ จงเขียนสมการคำนวณแผนที่ลักษณะสำคัญ (เอาต์พุต) ของชั้นคอนโวลูชั่น สำหรับ
(ก) คอนโวลูชั่นหนึ่งมิติ (มีชุดลำดับมิติชุดเดียว อินพุต \(\boldsymbol{X} \in \mathbb{R}^{C \times H}\) โดยชุดมิติแรกไม่มีความสัมพันธ์เชิงลำดับ).
(ข) คอนโวลูชั่นสามมิติ (มีชุดลำดับมิติสัมพันธ์สามชุด อินพุต \(\boldsymbol{X} \in \mathbb{R}^{C \times H \times W \times D}\) โดยชุดมิติแรกไม่มีความสัมพันธ์เชิงลำดับ).
(ค) คอนโวลูชั่นสี่มิติ (มีชุดลำดับมิติสัมพันธ์สี่ชุด อินพุต \(\boldsymbol{X} \in \mathbb{R}^{C \times H \times W \times D \times E}\) โดยชุดมิติแรกไม่มีความสัมพันธ์เชิงลำดับ).
6.0.0.1 การโปรแกรมตรรกะของโครงข่ายคอนโวลูชั่น.
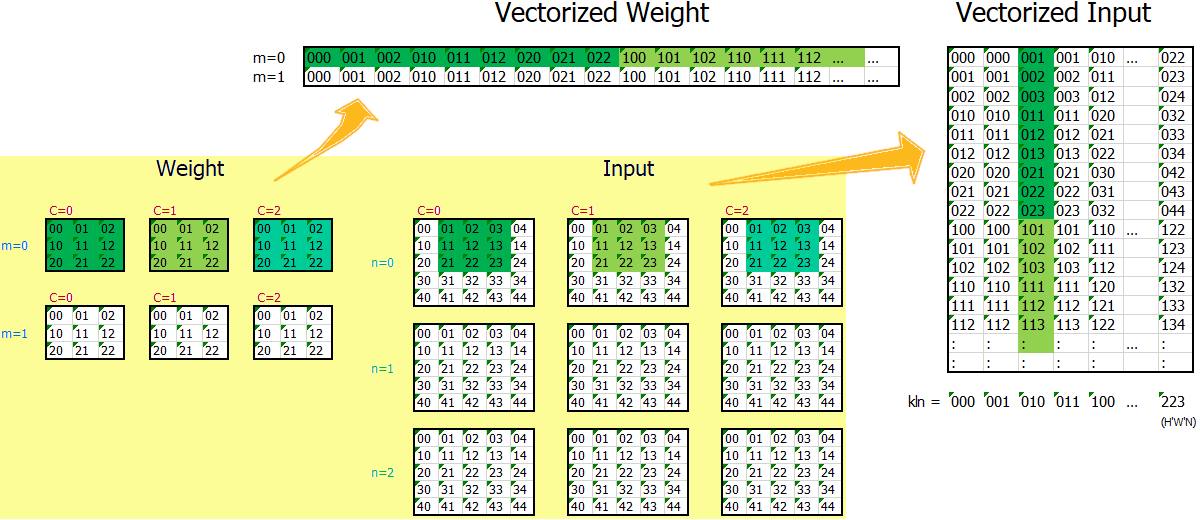
การคำนวณของโครงข่ายคอนโวลูชั่น ประกอบด้วยการคำนวณของชั้นคำนวณสามชนิดหลัก ๆ ได้แก่ ชั้นคำนวณคอนโวลูชั่น ชั้นดึงรวม และชั้นเชื่อมต่อเต็มที่. รายการ [code: MyConv2D] แสดงตัวอย่างโปรแกรมของชั้นคำนวณคอนโวลูชั่น. โปรแกรมในรายการ [code: MyConv2D] อาศัยการจัดเรียงเทนเซอร์ใหม่ และใช้ประโยชน์จากการคูณเมทริกซ์. รูป 1 แสดงแนวคิด การจัดเรียงเทนเซอร์ใหม่ เพื่อที่การคูณเมทริกซ์จะให้ผลลัพธ์เสมือนการคำนวณคอนโวลูชั่น. สังเกต สมการ \(\eqref{eq: deep conv conv FxCxHxW}\) เอาต์พุต \(\boldsymbol{a}\) เป็นเทนเซอร์สัดส่วน \(M \times H' \times W'\) (เมื่อ \(M\) เป็นจำนวนลักษณะสำคัญ และ \(H'\) กับ \(W'\) เป็นขนาดความสูงและกว้างของแผนที่เอาต์พุต) สำหรับจุดข้อมูลแต่ละจุด. ดังนั้น สำหรับชุดข้อมูลหมู่ขนาด \(N\) ผลลัพธ์จะเป็นเทนเซอร์สัดส่วน \(N \times M \times H' \times W'\). เอาต์พุต จากการคูณเมทริกซ์ \(\boldsymbol{W}_{M \times C \cdot H_f \cdot W_f} \cdot \boldsymbol{X}_{C \cdot H_f \cdot W_f \times H' \cdot W' \cdot N}\) จะเป็นเมทริกซ์ขนาด \(M \times H' \cdot W' \cdot N\) ซึ่งสามารถนำมาจัดเรียงเป็นเทนเซอร์สัดส่วน \(N \times M \times H' \times W'\) ได้.
หมายเหตุ การเขียนโปรแกรมคำนวณคอนโวลูชั่น เช่น สมการ \(\eqref{eq: deep conv conv FxCxHxW}\) ด้วยการวนลูป ก็สามารถทำได้ แต่การทำงานอาจทำได้ช้ามาก. ผู้อ่านสามารถทดลองวิธีการเขียนโปรแกรมหลาย ๆ แนวทาง และเปรียบเทียบข้อดีข้อเสีย ในแง่ต่าง ๆ เช่น ประสิทธิภาพการทำงาน ความยากง่ายในการแก้ไขและปรับปรุง.
class MyConv2D(nn.Module):
def __init__(self, input_channels, num_kernels, kernel_size,
stride=1, padding=0):
super(MyConv2D, self).__init__()
self.input_channels = input_channels
self.num_kernels = num_kernels
self.kernel_size = kernel_size
self.stride = stride
self.padding = padding
# initialization with pytorch default
sqk = torch.sqrt(torch.Tensor([1/(input_channels * \
kernel_size * kernel_size)]))
initw = 2*sqk*torch.rand(num_kernels, input_channels,
kernel_size, kernel_size) - sqk
initb = 2*sqk*torch.rand(num_kernels, 1) - sqk
self.weight = nn.Parameter(initw)
self.bias = nn.Parameter(initb)
def forward(self, z):
'''
(* {\color{blue} Eq.~\ref{eq: deep conv conv FxCxHxW}:\;
$a_{f,k,l}^{(v)} = b_f^{(v)} + \sum_{c=1}^C \sum_{i=1}^{H_F} \sum_{j=1}^{W_F} w_{fcij}^{(v)} \cdot z_{c, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j}^{(v-1)}$
} *)
'''
M, C, Hf, Wf = self.weight.shape
N, D, H, W = z.shape
assert C == D, 'Numbers of channels are not matched.'
S = self.stride
P = self.padding
# Determinte output size
Ho = int( (H + 2*P - Hf)/S ) + 1
Wo = int( (W + 2*P - Wf)/S ) + 1
# Simplify z structure
simplified_z = self._simplify_struct(z, Hf, Wf, S, P)
assert simplified_z.shape == (D * Hf * Wf, Ho * Wo * N)
simplified_w = self.weight.view(M,-1)
assert simplified_w.shape == (M, C * Hf * Wf)
# Compute convolution
simplified_out = self.bias +simplified_w.mm(simplified_z)
# Restructure convoluted output back
conv_out = simplified_out.view(M, Ho, Wo, N)
a = conv_out.permute(3, 0, 1, 2) # output (N, M, H', W')
return a
@staticmethod
def _simplify_struct(z, Hf, Wf, S, P):
'''
Collapse z structure such that convolution can be
efficiently computed as matrix multiplication.
'''
# Zero-pad the input (on last 2 dimensions)
zhat = torch.nn.functional.pad(z, (P,P,P,P,0,0,0,0),
'constant', 0)
# Get vectorized indices
c, rx, cx = MyConv2D._get_simplified_indices(z.shape,
Hf, Wf, S, P)
# c.shape = (C Hf Wf, 1)
# rx.shape = (C Hf Wf, Ho Wo)
# cx.shape = (C Hf Wf, Ho Wo)
# Re-arrange input into a simplified structure
simz = zhat[:, c, rx, cx] # shape (N, C Hf Wf, Ho Wo)
num_channels = z.shape[1]
sim_z = simz.permute(1, 2, 0).contiguous().view(\
num_channels * Hf * Wf, -1)
return sim_z # shape = (C Hf Wf, Ho Wo N)
@staticmethod
def _get_simplified_indices(input_shape, Hf, Wf, S, P):
'''
return indices of re-arranged vector ready for
dot operation (in lieu of convolution).
'''
N, C, H, W = input_shape
# Determinte output size
Ho = int( (H + 2*P - Hf)/S ) + 1
Wo = int( (W + 2*P - Wf)/S ) + 1
# To match the re-arranged weight,
# input must be re-arranged accordingly.
# weight row: f = 0, 1, ..., (M-1)
# weight column: cij = 000, 001, 002, 010, 011, ...
# Thus, input row: cij
# input column: k,l = 00, 01, 02, ..., (Ho-1)(Wo-1)
# Work out indices of filter nodes
# j, i, c from innermost to outermost along row direction
j = np.tile(np.arange(Wf), Hf * C).reshape(-1, 1)
# e.g., j = [0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, ...]
i = np.tile(np.repeat(np.arange(Hf),Wf),C).reshape(-1, 1)
# e.g., i = [0, 0, 0, 1, 1, 1, 2, 2, 2, 0, 0, 0, ...]
c = np.repeat(np.arange(C), Hf*Wf).reshape(-1, 1)
# e.g., c = [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, ...]
# Work out indices of output nodes
# l, k from innermost to outermost, along column
l = np.tile(np.arange(Wo), Ho).reshape(1, -1)
# e.g., l.T = [0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, ...]
k = np.repeat(np.arange(Ho), Wo).reshape(1, -1)
# e.g., k.T = [0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, ...]
# Indices of input nodes
rx = S * k + i # shape = (C Hf Wf, Ho Wo)
cx = S * l + j # shape = (C Hf Wf, Ho Wo)
return c.astype(int), rx.astype(int), cx.astype(int) โปรแกรมในรายการ [code: net MyConv2D] แสดงตัวอย่างการเรียกใช้ MyConv2D. โปรแกรม MyConv2D เขียนขึ้นตามรูปแบบของไพทอร์ช nn.Conv2d ดังนั้น การใช้งานก็ทำในลักษณะเดียวกันได้. โปรแกรมในรายการ [code: train net MyConv2D] และ [code: test net MyConv2D] แสดงตัวอย่างฝึกและทดสอบโครงข่าย (ค่าอภิมานพารามิเตอร์ต่าง ๆ ใช้ได้ดีกับชุดข้อมูลเอมนิสต์. ดูแบบฝึกหัด [ex: torch dataloader built-in mnist] สำหรับตัวอย่างการนำเข้าชุดข้อมูลเอมนิสต์).
class NetConv1(nn.Module):
def __init__(self):
super(NetConv1, self).__init__()
self.conv1 = MyConv2D(1, 16, 5, 1, 2)
self.pool1 = nn.MaxPool2d(2, 2)
self.conv2 = MyConv2D(16, 8, 3, 1, 1)
self.pool2 = nn.MaxPool2d(2, 2)
self.fc1 = nn.Linear(8*7*7, 10)
def forward(self, x):
z1 = torch.relu(self.conv1(x))
z2 = self.pool1(z1)
z3 = torch.relu(self.conv2(z2))
z4 = self.pool2(z3)
z5 = z4.view(-1, 8 * 7 * 7)
a6 = self.fc1(z5)
return a6
net = NetConv1().to(device)
loss_fn = torch.nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters(), lr=0.001)num_epochs = 20
N = len(trainloader) * 50 # 50 samples a batch
for epoch in range(num_epochs):
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
inputs, labels = data
optimizer.zero_grad()
outputs = net(inputs.to(device))
loss = loss_fn(outputs.to('cpu'), labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
# end for i
print('Epoch %d loss: %.3f' % (epoch + 1, running_loss / N))
torch.save(net.state_dict(), './conv1_net.pth')net.eval()
N = len(testloader) * 50 # 50 samples a batch
correct = 0
for i, data in enumerate(testloader):
inputs, labels = data
outputs = net(inputs.to(device))
yhat = outputs.to('cpu')
yhatc = torch.argmax(outputs, 1)
correct += torch.sum(yhatc.cpu() == labels).numpy()
print('Correct %d out of %d'%(correct, N))
print('Accuracy %.3f'%(correct/N))6.0.0.1.1 แบบฝึกหัด
จงศึกษาการทำงานของชั้นคำนวณคอนโวลูชั่นและวิธีการเขียนโปรแกรมในรายการ [code: MyConv2D] แล้วทดสอบการทำงานเปรียบเทียบกับโปรแกรมสำเร็จรูป nn.Conv2d รวมถึงทดสอบโครงสร้างแบบอื่น ๆ (เปลี่ยนค่าอภิมานพารามิเตอร์ เช่น ขนาดฟิลเตอร์ จำนวนฟิลเตอร์ ขนาดก้าวย่าง จำนวนการเติมเต็มด้วยศูนย์) อภิปรายและสรุป. หมายเหตุ ในทางปฏิบัติ การใช้โปรแกรมสำเร็จรูปจะสะดวกกว่า การอ้างอิงก็ทำได้ง่ายกว่า ถูกยอมรับดีกว่า (โปรแกรมมาตราฐาน เชื่อว่าได้รับการตรวจสอบมาดีกว่า) และดังเช่นที่จะได้เห็นจากการทดลอง ในกรณีนี้ โปรแกรมสำเร็จรูป nn.Conv2d ทำงานได้มีประสิทธิภาพมากกว่าอย่างเห็นได้ชัด (การเขียนโปรแกรมประสิทธิภาพสูง อาจต้องอาศัยการโปรแกรมระดับล่าง ซึ่งอยู่นอกเหนือขอบเขตของหนังสือเล่มนี้). แต่การศึกษาโปรแกรมในรายการ [code: MyConv2D] ทำเพื่อให้เข้าใจกลไกการทำงานของชั้นคำนวณคอนโวลูชั่นอย่างกระจ่างแจ้ง.
6.0.0.1.2 แบบฝึกหัด
การเขียนโปรแกรมชั้นเชื่อมต่อเต็มที่ก็สามารถทำได้ในลักษณะเดียวกัน. รายการ [code: MyFCBack] แสดงตัวอย่างโปรแกรมเชื่อมต่อเต็มที่ที่เขียนการแพร่กระจายย้อนกลับเอง โดยการคำนวณจริงทำผ่านการเรียกฟังก์ชัน fcf ที่เขียนดังในรายการ [code: fcf]. การใช้งานชั้นเชื่อมต่อเต็มที่ MyFCBack ก็ทำเช่นเดียวกับการเรียกใช้ชั้นคำนวณ nn.Linear เช่น การเปลี่ยนบรรทัดคำสั่ง self.fc1 = nn.Linear(8*7*7, 10) ในรายการ [code: net MyConv2D] เป็น self.fc1 = MyFCBack(8*7*7, 10) เท่านั้น ที่เหลือก็สามารถดำเนินงานสร้างโครงข่าย ฝึก และทดสอบได้เช่นเดิม.
class fcf(torch.autograd.Function):
@staticmethod
def forward(ctx, zp, w, b):
# input: zp (N,Mi): (* {\color{blue} $z_j^{(v-1)}$ } *) , w (Mo,Mi): (* {\color{blue} $\partial w^{(v)}_{ji}$ } *) , b (Mo,1): (* {\color{blue} $\partial b^{(v)}_{j}$ } *)
# output: a (N,Mo): (* {\color{blue} $a_j^{(v)}$ } *)
zT = torch.transpose(zp, 0, 1)
a = w.mm(zT) + b
ctx.save_for_backward(zp, w, b)
return torch.transpose(a, 0, 1)
@staticmethod
def backward(ctx, dEa):
# input: dEa (N,Mo): (* {\color{blue} $\frac{\partial E}{\partial a^{(v)}_j}$ }*)
# output: dEzp: (* {\color{blue} $\frac{\partial E}{\partial z^{(v-1)}_i} = \sum_j \frac{\partial E}{\partial a^{(v)}_j} \cdot \frac{\partial a^{(v)}_j}{\partial z^{(v-1)}_i}$ } *) , dEw: (* {\color{blue} $\frac{\partial E}{\partial w^{(v)}_{ji}} = \frac{\partial E}{\partial a^{(v)}_j} \cdot \frac{\partial a^{(v)}_j}{\partial w^{(v)}_{ji}}$ } *) , dEb: (* {\color{blue} $\frac{\partial E}{\partial b^{(v)}_{j}} = \frac{\partial E}{\partial a^{(v)}_j} \cdot \frac{\partial a^{(v)}_j}{\partial b^{(v)}_{j}}$ } *)
N, _ = dEa.shape
zp, w, b = ctx.saved_tensors
dEzp = dEa.mm(w)
dEw = torch.transpose(dEa, 0, 1).mm(zp)
dEb = torch.transpose(dEa, 0, 1).mm(torch.ones(N,1).to(dEa.device))
return dEzp, dEw, dEbclass MyFCBack(nn.Module):
def __init__(self, input_channels, num_features):
super(MyFCBack, self).__init__()
self.input_channels = input_channels
self.num_features = num_features
sqk = torch.sqrt(torch.Tensor([1/input_channels]))
initw = 2*sqk*torch.rand(num_features,input_channels)-sqk
initb = 2*sqk*torch.rand(num_features,1) - sqk
self.weight = nn.Parameter(initw)
self.bias = nn.Parameter(initb)
self.fcf = fcf.apply
def forward(self, z):
a = self.fcf(z, self.weight, self.bias)
return aจงทดสอบการทำงานของชั้นเชื่อมต่อเต็มที่ MyFCBack เปรียบเทียบกับโปรแกรมสำเร็จรูป nn.Linear ทั้งในเชิงการทำงาน และเวลาในการทำงาน. รวมถึง จงทดลองแก้การคำนวณในฟังก์ชัน fcf เพื่อตรวจสอบดูว่าการคำนวณการเชื่อมต่อและการคำนวณแพร่กระจายย้อนกลับ ว่าได้ทำผ่าน fcf.forward และ fcf.backward จริง. ตัวอย่างเช่น ทดลองแก้บรรทัดคำสั่ง return dEzp, dEw, dEb เป็น return 0*dEzp, 0*dEw, 0*dEb และสังเกตผล. สรุป และอภิปราย.
หมายเหตุ แม้การเขียนโปรแกรมชั้นเชื่อมต่อเต็มได้ถูกอภิปรายไปแล้วในหัวข้อ [section: deep exercises] การทบทวนอีกครั้งในแบบฝึกหัด เพื่อให้คุ้นเคยกับรูปแบบการเขียนโปรแกรมชั้นคำนวณ เพื่อใช้กับไพทอร์ช ที่ระบุการคำนวณการแพร่กระจายย้อนกลับด้วย. การทบทวนนี้ จะคาดว่าจะช่วยผู้อ่านเข้าใจกลไกของการเขียนโปรแกรมชั้นคำนวณพร้อมการระบุการแพร่กระจายย้อนกลับของไพทอร์ช ก่อนที่จะเขียนโปรแกรมชั้นคอนโวลูชั่น ซึ่งซับซ้อนขึ้นในแบบฝีกหัด 1.0.0.1.3.
6.0.0.1.3 แบบฝึกหัด
คล้ายกับแบบฝึกหัด 1.0.0.1.2 แบบฝึกหัดนี้ศึกษาการเขียนโปรแกรมชั้นคอนโวลูชั่นทั้งการคำนวณ และการแพร่กระจายย้อนกลับ. รายการ [code: MyConv2DB] แสดงตัวอย่างโปรแกรมชั้นคอนโวลูชั่นที่เขียนการแพร่กระจายย้อนกลับเอง โดยการคำนวณจริงทำผ่านการเรียกฟังก์ชัน convf ที่เขียนดังในรายการ [code: convf] 1. โปรแกรมชั้นคอนโวลูชั่น MyConv2DB รับมรดกมาจาก MyConv2D (รายการ [code: MyConv2D]) เพื่อลดความซ้ำซ้อน ที่จะต้องกำหนดค่าเริ่มต้นค่าน้ำหนัก (ภายในเมท็อด __init__). การใช้งานชั้นคอนโวลูชั่น MyConv2DB ก็ทำเช่นเดียวกับ MyConv2D เช่น การเปลี่ยนบรรทัดคำสั่ง self.conv1 = MyConv2D(1, 16, 5, 1, 2) และบรรทัดคำสั่ง self.conv2 = MyConv2D(16, 8, 3, 1, 1) ในรายการ [code: net MyConv2D] เป็น self.conv1 = MyConv2DB(1, 16, 5, 1, 2) และ self.conv2 = MyConv2D(16, 8, 3, 1, 1) ตามลำดับ เท่านั้น ที่เหลือก็สามารถดำเนินงานสร้างโครงข่าย ฝึก และทดสอบได้เช่นเดิม.
class convf(torch.autograd.Function):
@staticmethod
def forward(ctx, zp, w, b, S, P):
'''
(* {\color{blue} Eq.~\ref{eq: deep conv conv FxCxHxW}:\;
$a_{f,k,l}^{(v)} = b_f^{(v)} + \sum_{c=1}^C \sum_{i=1}^{H_F} \sum_{j=1}^{W_F} w_{fcij}^{(v)} \cdot z_{c, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j}^{(v-1)}$
} *)
(* {\color{blue} zp: $z_{cij}^{(v-1)}$, w: $w_{fcij}^{(v)}$, b: $b_f^{(v)}$, S: stride, P: padding } *)
'''
F, C, Hf, Wf = w.shape
N, D, H, W = zp.shape
assert C == D, 'Numbers of channels are not matched.'
# Determinte output size
Ho = int( (H + 2*P - Hf)/S ) + 1
Wo = int( (W + 2*P - Wf)/S ) + 1
# Simplify z structure
simplified_z = MyConv2D._simplify_struct(zp,Hf,Wf,S,P)
assert simplified_z.shape == (D * Hf * Wf, Ho * Wo * N)
simplified_w = w.view(F,-1)
assert simplified_w.shape == (F, C * Hf * Wf)
# Compute convolution
simplified_out = b + simplified_w.mm(simplified_z)
# Restructure convoluted output back
conv_out = simplified_out.view(F, Ho, Wo, N)
a = conv_out.permute(3, 0, 1, 2) # output (N, M, H', W')
ctx.save_for_backward(zp, w, b, torch.tensor([S, P]),
simplified_z)
return a
@staticmethod
def backward(ctx, dEa):
# input: dEa (N, F, H', W'): (* {\color{blue} $\delta^{(v)}_{qrs} = \frac{\partial E}{\partial a^{(v)}_{qrs}}$ }*)
# output: dEzp (N, C, H, W): (* {\color{blue} $\hat{\delta}^{(v-1)}_{fkl} = \frac{\partial E}{\partial z^{(v-1)}_{fkl}} = \sum_{q=1}^F \sum_{r \in \Omega_r} \sum_{s \in \Omega_s} \delta_{qrs}^{(v)} \cdot w_{q,f,k-S_H \cdot (r - 1),l-S_W \cdot (s - 1)}^{(v)}$ } *)
# dEw (F, C, Hf, Wf): (* {\color{blue} $\frac{\partial E}{\partial w_{qfij}^{(v)}} = \sum_{r=1}^{H} \sum_{s=1}^{W} \delta_{qrs}^{(v)} z_{f, S_H \cdot (r-1)+i, S_W \cdot (s-1)+j}^{(v-1)}$ } *)
# dEb (F,1): (* {\color{blue} $\frac{\partial E_n}{\partial b_q^{(v)}} = \sum_{r=1}^{H} \sum_{s=1}^{W} \delta_{qrs}^{(v)}$ } *)
N, F, Ho, Wo = dEa.shape
zp, w, b, tensorSP, simplified_z = ctx.saved_tensors
S = tensorSP[0].item()
P = tensorSP[1].item()
_, C, Hf, Wf = w.shape
# Calculate dEb
dEb = dEa.sum(dim=(0,2,3)).view(-1,1) # sum over N,H',W'
# Restructure dEa from (N, F, H', W') to (F, H' W' N)
simplified_dEa = dEa.permute(1, 2, 3, 0).contiguous().view(F, -1)
# Calculate dEw
dEw = simplified_dEa.mm(simplified_z.transpose(0,1))
dEw = dEw.view(w.shape) # (F, C, Hf, Wf)
# Calculate dEzp (N, C, H, W): (* {\color{blue} $\hat{\delta}^{(v-1)}_{fkl} = \frac{\partial E}{\partial z^{(v-1)}_{fkl}}$} *)
# (* {\color{blue} $\frac{\partial E}{\partial z^{(v-1)}_{fkl}} = \sum_{q=1}^F \sum_{r \in \Omega_r} \sum_{s \in \Omega_s} \delta_{qrs}^{(v)} \cdot w_{q,f,k-S_H \cdot (r - 1),l-S_W \cdot (s - 1)}^{(v)} = \sum_{r \in \Omega_r} \sum_{s \in \Omega_s} (\sum_{q=1}^F \delta_{qrs}^{(v)} \cdot w_{q,f,k-S_H \cdot (r - 1),l-S_W \cdot (s - 1)}^{(v)})$ } *)
# First, sum over the feature axis
simplified_w = w.view(F,-1)
assert simplified_w.shape == (F, C * Hf * Wf)
wdEa_overF = simplified_w.transpose(0,1).mm(
simplified_dEa) #(C Hf Wf, H'W'N)
# Sum over spatial indices
dEzp = convf.sum_omega(wdEa_overF,zp.shape,Hf,Wf,P,S)
return dEzp, dEw, dEb, None, None
@staticmethod
def sum_omega(prod_overF, zpshape, Hf, Wf, P, S):
'''
Summation over the two omega sets (~over H' and W')
input: prod_overF (C Hf Wf, H' W' N): (* {\color{blue} $(\sum_{q=1}^F \delta_{qrs}^{(v)} \cdot w_{q,f,k-S_H \cdot (r - 1),l-S_W \cdot (s - 1)}^{(v)})$ } *)
output: dEzp (N, C, H, W): (* {\color{blue} $\hat{\delta}^{(v-1)}_{fkl} = \frac{\partial E}{\partial z^{(v-1)}_{fkl}} = \sum_{r \in \Omega_r} \sum_{s \in \Omega_s} (\sum_{q=1}^F \delta_{qrs}^{(v)} \cdot w_{q,f,k-S_H \cdot (r - 1),l-S_W \cdot (s - 1)}^{(v)})$ } *)
'''
N, C, H, W = zpshape
H_hat, W_hat = H + 2*P, W + 2*P
# Restructure prod_overF for sum over omega
prod_overF_reshaped = prod_overF.view(C*Hf*Wf, -1, N)
prod = prod_overF_reshaped.permute(2, 0, 1).cpu().numpy()
# Prepare result structure
sum_result = np.zeros((N,C,H_hat,W_hat),dtype=prod.dtype)
# Get vectorized indices
c, rx, cx = MyConv2D._get_simplified_indices(zpshape,
Hf, Wf, S, P)
# c.shape = (C Hf Wf, 1)
# rx.shape = (C Hf Wf, H' W')
# cx.shape = (C Hf Wf, H' W')
# Sum over omega using np.add.at mechanism
np.add.at(sum_result, (slice(None), c, rx, cx), prod)
tsum = torch.tensor(sum_result).to(prod_overF.device)
if P != 0:
# remove side effect from padding
return tsum[:, :, P:-P, P:-P]
return tsumclass MyConv2DB(MyConv2D):
def __init__(self, input_channels, num_kernels,
kernel_size, stride=1, padding=0):
super(MyConv2DB, self).__init__(input_channels,
num_kernels, kernel_size, stride, padding)
self.convf = convf.apply
def forward(self, z):
a = self.convf(z, self.weight, self.bias,
self.stride, self.padding)
return aจงทดสอบชั้นคำนวณ MyConv2DB ทั้งในเชิงผลการทำงาน และประสิทธิภาพการทำงาน (วัดเวลาทำงาน) รวมถึงทดสอบว่า การแพร่กระจายย้อนกลับทำผ่าน convf.backward จริง (ดูแบบฝึกหัด 1.0.0.1.2 ประกอบ). แล้วเปรียบเทียบกับโปรแกรมสำเร็จรูป nn.Conv2d.
หมายเหตุ การเขียนโปรแกรมเองในที่นี้เพื่อความกระจ่างในกลไกการทำงาน แต่ในทางปฏิบัติ แนะนำให้ใช้โปรแกรมสำเร็จรูป ด้วยเหตุผลด้านความสะดวก ประสิทธิภาพ การทดสอบที่ดีและครอบคลุมกว่า รวมถึงความยอมรับและความไว้วางใจของผู้เกี่ยวข้อง.
6.0.0.1.4 แบบฝึกหัด
แบบฝึกหัดนี้ศึกษาการเขียนโปรแกรมชั้นดึงรวมแบบมากที่สุด ทั้งการคำนวณ และการแพร่กระจายย้อนกลับ. รายการ [code: MyMaxpool] แสดงตัวอย่างโปรแกรมชั้นดึงรวมแบบมากที่สุด ที่เขียนการแพร่กระจายย้อนกลับเอง โดยการคำนวณจริงทำผ่านการเรียกฟังก์ชัน maxpoolf ที่เขียนดังในรายการ [code: maxpoolf] 2. การใช้งานชั้นดึงรวม MyMaxpool ก็ทำเช่นเดียวกับโปรแกรมสำเร็จรูป nn.MaxPool2d เช่น การเปลี่ยนบรรทัดคำสั่ง self.pool1 = nn.MaxPool2d(2,2) และ self.pool2 = nn.MaxPool2d(2, 2) ในรายการ [code: net MyConv2D] เป็น self.pool1 = MyMaxpool(2, 2, 0) และ self.pool2 = MyMaxpool(2, 2, 0) ตามลำดับ เท่านั้น. ส่วนที่เหลือก็สามารถดำเนินงานสร้างโครงข่าย ฝึก และทดสอบได้เช่นเดิม.
class maxpoolf(torch.autograd.Function):
@staticmethod
def forward(ctx, zp, Hf=2, Wf=2, S=2, P=0):
'''
input: zp (N, C, H, W): (* {\color{gray} $z_{c,i,j}^{(v-1)}$} *)
output: z (N,C,H',W'): (* {\color{gray} $z_{c,k,l}^{(v)} = g( \{ z_{c, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j}^{(v-1)} \}_{i=1,\ldots, H_F, j=1,\ldots, W_F} )$} *)
'''
N, C, H, W = zp.shape
# Determinte output size
Ho = int( (H + 2*P - Hf)/S ) + 1
Wo = int( (W + 2*P - Wf)/S ) + 1
# Restructure zp
# An operation effect of pooling is different from conv
# such that channel/feature axis is treated independently
# (like datapoint axis).
restruct_z = zp.view(N * C, 1, H, W)
sim_z = MyConv2D._simplify_struct(restruct_z, Hf,Wf,S,P)
assert sim_z.shape == (Hf * Wf, Ho * Wo * N * C)
# Perform pooling function
# poolz, pool_cache = pool_func(sim_z)
max_idx = torch.argmax(sim_z, dim=0)
poolz = sim_z[max_idx, range(max_idx.size()[0])]
pool_cache = max_idx
# Restructure pooling output
zpool = poolz.view(Ho, Wo, N, C)
z = zpool.permute(2, 3, 0, 1).contiguous()
ctx.save_for_backward(zp, torch.tensor([Hf, Wf, S, P]),
sim_z, pool_cache)
return z
@staticmethod
def backward(ctx, dEz):
# input: dEz (N, F, H', W'): (* {\color{blue} $\hat{\delta}_{frs}^{(v)}$} *)
# output: dEzp (N, F, H, W): (* {\color{blue} $\hat{\delta}_{fkl}^{(v-1)} = \sum_{r \in \Omega_r} \sum_{s \in \Omega_s} \hat{\delta}_{frs}^{(v)} \frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}}$ }*)
zp, tensorHfWfSP, sim_z, pool_cache = ctx.saved_tensors
Hf = tensorHfWfSP[0].item()
Wf = tensorHfWfSP[1].item()
S = tensorHfWfSP[2].item()
P = tensorHfWfSP[3].item()
N, F, H, W = zp.shape
sim_dEa = torch.zeros(sim_z.shape).to(zp.device)
sim_dEz = dEz.permute(2, 3, 0, 1).contiguous().view(-1,)
# Perform dpooling function
# sim_dEa = dpool_func(poolz, pool_cache)
# sim_dEa: (* {\color{blue} $\hat{\delta}_{frs}^{(v)} \cdot \frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}} = \left\{\begin{array}{l l}\delta_{frs}^{(v)} & \;\mbox{when}\; f, k, l \;\mbox{are the max id's}\\ 0 & \;\mbox{otherwise}\end{array}\right.$} *)
sim_dEa[pool_cache, range(pool_cache.size()[0])] =
sim_dEz # (Hf Wf, H' W' N F)
# Sum over spatial indices
dEzp_sim = convf.sum_omega(sim_dEa,
(N*F, 1, H, W), Hf, Wf, P, S)
dEzp = dEzp_sim.view(zp.shape)
return dEzp, None, None, None, None
class MyMaxpool(nn.Module):
def __init__(self, kernel_size, stride, padding=0):
super(MyMaxpool, self).__init__()
self.maxpoolf = maxpoolf.apply
self.Hf = kernel_size
self.Wf = kernel_size
self.stride = stride
self.padding = padding
def forward(self, zp):
z = self.maxpoolf(zp, self.Hf, self.Wf,
self.stride, self.padding)
return zจงทดสอบชั้นคำนวณ MyMaxpool ทั้งในเชิงผลการทำงาน และประสิทธิภาพการทำงาน (วัดเวลาทำงาน) รวมถึงทดสอบว่า การแพร่กระจายย้อนกลับทำผ่าน maxpoolf.backward จริง. แล้วเปรียบเทียบกับโปรแกรมสำเร็จรูป nn.MaxPool2d.
หมายเหตุ การเขียนโปรแกรมเองในที่นี้เพื่อความกระจ่างในกลไกการทำงาน แต่ในทางปฏิบัติ แนะนำให้ใช้โปรแกรมสำเร็จรูป ด้วยเหตุผลด้านความสะดวก ประสิทธิภาพ การทดสอบที่ดีและครอบคลุมกว่า รวมถึงความยอมรับและความไว้วางใจของผู้เกี่ยวข้อง.