6 โครงข่ายคอนโวลูชั่น
“Adapt or perish, now as ever, is nature’s inexorable imperative.”
—H. G. Wells
“ปรับตัว หรือ สูญพันธ์ไป เป็นความจริงของธรรมชาติที่ไม่อาจหลีกเลี่ยงได้ ทั้งตอนนี้และเฉกเช่นเสมอมา.”
—เอช จี เวลส์
ดังที่กล่าวในบทที่ [chapter: Deep Learning] โครงข่ายคอนโวลูชั่น เป็นศาสตร์และศิลป์ที่สำคัญของการเรียนรู้ของเครื่อง. โครงข่ายคอนโวลูชั่น อาศัยโครงสร้างที่เหมาะสมกับ ข้อมูลที่มีรูปแบบเชิงท้องถิ่นสูง ซึ่งข้อมูลในงานคอมพิวเตอร์วิทัศน์ ก็มีลักษณะเช่นนี้. งานคอมพิวเตอร์วิทัศน์ เป็นงานแรก ๆ ที่ โครงข่ายคอนโวลูชั่น ได้พิสูจน์ให้เห็นศักยภาพของการเรียนรู้เชิงลึก และปัจจุบัน โครงข่ายคอนโวลูชั่น ได้กลายเป็นศาสตร์และศิลป์ของคอมพิวเตอร์วิทัศน์ในหลาย ๆ ด้าน. ยาน เลอคุน (Yann LeCun) ผู้เชี่ยวชาญการเรียนรู้เชิงลึก และผู้บุกเบิกการใช้งานโครงข่ายคอนโวลูชั่น ยกย่อง โครงข่ายคอนโวลูชั่น ว่าเป็นส่วนที่นำพัฒนาการที่สำคัญมาให้กับวงการประมวลผลภาพ วิดีโอ คำพูด และเสียง.
โครงข่ายคอนโวลูชั่น (Convolutional Neural Network คำย่อ CNN) เป็นโครงข่ายประสาทเทียม ที่จำกัดการเชื่อมต่อของหน่วยย่อย และมีการใช้ค่าน้ำหนักร่วมกัน. โครงข่ายคอนโวลูชั่น ถูกออกแบบมาสำหรับข้อมูลที่มีลักษณะเชิงท้องถิ่นสูง และรูปแบบเชิงท้องถิ่นมีลักษณะร่วมกัน. ดังนั้นเมื่อใช้กับข้อมูลที่มีลักษณะเชิงท้องถิ่น การจำกัดการเชื่อมต่อและการใช้ค่าน้ำหนักร่วมกัน จึงช่วยเพิ่มประสิทธิภาพ การคำนวณอนุมานและการฝึกโครงข่ายขึ้นอย่างมาก เพราะ ได้ลดภาระการคำนวณของการเชื่อมต่อที่มีผลกระทบน้อยออกไป และสามารถใช้สารสนเทศในแต่ละจุดข้อมูลได้คุ้มค่ามากขึ้น.
ข้อมูลหลาย ๆ ชนิด มีลักษณะเชิงท้องถิ่นสูง และเป็นลักษณะเชิงท้องถิ่นภายใต้โครงสร้างของลำดับมิติ เช่น ภาพสเกลเทา ถูกแทนด้วยข้อมูลสองลำดับชั้นของค่าความเข้มพิกเซล (ลำดับค่าพิกเซลในแกนนอน และลำดับค่าพิกเซลในแกนตั้ง), ภาพสี ถูกแทนด้วยข้อมูลสามลำดับชั้น (ลำดับค่าพิกเซลในแกนนอน, ลำดับค่าพิกเซลในแกนตั้ง, และชุดของช่องสีแดงเขียวน้ำเงิน), ภาพมัลติสเปกตรัม (multispectral image) ถูกแทนด้วยข้อมูลหลายลำดับชั้น (ลำดับค่าพิกเซลในแกนนอน, ลำดับค่าพิกเซลในแกนตั้ง, และชุดต่าง ๆ แต่ละชุดแทนค่าของแต่ละสเปกตรัม) วิดีโอถูกแทนด้วยลำดับของภาพ, เสียงถูกแทนด้วยสเปกโตแกรมเสียง (audio spectogram), ภาษาเขียนถูกแทนด้วยลำดับของอักขระ เป็นต้น.
การที่กล่าวว่า ข้อมูลมีลักษณะเชิงท้องถิ่น คือตัวอย่างเช่น ภาพถ่ายมุมสูงของหมู่บ้าน ภายในภาพจะเห็นบริเวณและตัวบ้านหลาย ๆ หลัง. รูปแบบของบ้านแต่ละหลัง จะสังเกตได้ทันทีจากตัวบ้านและบริเวณใกล้เคียง โดยไม่ต้องอาศัยส่วนอื่นของภาพที่อยู่ห่างออกไปประกอบ. นอกจากนั้น ภาพของหมู่บ้านภาพเดียว อาจแสดงรูปแบบของบ้านหลาย ๆ หลัง และแม้ว่าบ้านแต่หลังอาจแตกต่างกัน แต่มักจะมีลักษณะบางอย่างร่วมกันอยู่ เช่น อาจจะเป็น ขนาด รูปทรง หรือวัสดุที่ใช้ทำหลังคา. นั่นคือ นอกจากรูปแบบของบ้านจะมีลักษณะเชิงท้องถิ่นแล้ว รูปแบบเชิงท้องถิ่นยังมีลักษณะร่วมกันอีกด้วย ซึ่งลักษณะร่วมเช่นนี้ ที่ทำให้วิธีการใช้ค่าน้ำหนักร่วมของโครงข่ายคอนโวลูชั่น สามารถใช้ประโยชน์จากแต่ละจุดข้อมูลได้คุ้มค่า เช่น การเรียนรู้รูปแบบของบ้าน จากส่วนภาพของบ้านหลาย ๆ หลัง ที่ปรากฏในภาพเดียวกัน.
6.0.0.0.1 โครงข่ายคอนโวลูชั่น กับมิติและลำดับชั้นของข้อมูล.
บทที่ [chapter: background] ได้อธิบาย ความหมายของมิติจากมุมมองต่าง ๆ และแนะนำความหมายของลำดับชั้น. ลำดับชั้น (rank) คือโครงสร้างลำดับมิติ หรือชุดมิติ.
โครงสร้างของโครงข่ายประสาทเทียมดั่งเดิม มองข้อมูลในรูปมิติที่ไม่มีโครงสร้างระหว่างมิติ ตัวอย่างเช่น ข้อมูลชุดภาพเอ็กซเรย์เต้านมของมวลเนื้อ (แบบฝึกหัด [ex: mammography]) แต่ละจุดข้อมูลจะมี \(6\) เขตข้อมูล ซึ่ง เขตข้อมูลความร้ายแรงเป็นเอาต์พุต และเขตข้อมูล (1) ค่าการประเมินไบแรตส์, (2) อายุของผู้ป่วย, (3) รูปทรงของมวลเนื้อ, (4) ลักษณะขอบของมวลเนื้อ, และ (5) ความหนาแน่นของมวลเนื้อ เป็นอินพุต. นั่นคือ อินพุตของข้อมูลชุดนี้มี \(5\) มิติ เขตข้อมูลในแต่ละมิติ ไม่ได้เกี่ยวกันในเชิงโครงสร้าง นั่นคือ การดำเนินการ โดยสลับลำดับของเขตข้อมูล จะไม่ได้ทำให้สารสนเทศของข้อมูลเสียหาย.
เปรียบเทียบกับข้อมูลที่มิติเกี่ยวพันกันในเชิงโครงสร้าง การสลับลำดับจะทำให้สูญเสียสารสนเทศของข้อมูลไป. ดังหากพิจารณาข้อมูลในรูปแบบที่มีมิติลำดับตามธรรมชาติ เช่น ข้อมูลภาพสีในรูป 1.1. ข้อมูลภาพมีโครงสร้างมิติที่ชัดเจน นั่นคือมี (1) ชุดมิติของสี ที่มีสำหรับสีน้ำเงิน เขียว และแดง (2) ชุดลำดับมิติของพิกเซลตามแนวตั้ง และ (3) ชุดลำดับมิติของพิกเซลตามแนวนอน. หากแต่ละค่าความเข้มพิกเซลมีค่าอยู่ระหว่าง \(0\) ถึง \(255\) สามารถใช้ เทนเซอร์ลำดับชั้นสาม \(\boldsymbol{X} \in \{0, \ldots, 255\}^{3 \times 133 \times 175}\) สำหรับแทนภาพสีหนึ่งภาพ ขนาดสูง \(133\) พิกเซล และกว้าง \(175\) พิกเซลได้. ข้อมูลลักษณะนี้ แม้ว่า แต่ละจุดข้อมูล (แต่ละภาพ) จะมี \(69825\) ค่า (ภาพหนึ่งภาพดังตัวอย่าง ต้องการหน่วยความจำ \(69825\) ไบต์) แต่ค่าเหล่านี้ มีความสัมพันธ์กันเชิงลำดับด้วย เช่น ถ้าค่าพิกเซลที่อยู่ติด ๆ กันมีค่าใกล้เคียงกัน นั่น อาจหมายถึงลายเส้นที่สื่อความหมาย และแม้จะมีบางค่าพิกเซลขาดหรือเกินไปบ้าง ความหมายก็ไม่ได้เปลี่ยนแปลง. ความหมายได้จากผลเชิงรวมของค่าพิกเซลบริเวณใกล้เคียงกัน. การที่ค่าต่าง ๆ บริเวณใกล้เคียงมีความสัมพันธ์ต่อกันในเชิงความหมายรวม จะเรียกว่า ลักษณะเชิงท้องถิ่น.

โครงข่ายประสาทเทียมดั่งเดิม ไม่มีกลไกที่รองรับลำดับมิติ แต่ก็สามารถนำข้อมูลที่มีลำดับมิติเข้าไปประมวลผลได้ โดยการยุบชุดลำดับมิติรวมกัน เช่น จุดข้อมูล \(\boldsymbol{X} \in \mathbb{R}^{3 \times 133 \times 175}\) ยุบเป็นจุดข้อมูล \(\boldsymbol{x} \in \mathbb{R}^{69825}\). แม้ว่า ข้อมูลที่มีลำดับมิติจะสามารถถูกยุบได้ แต่การทำเช่นนี้จะทำให้โครงสร้างธรรมชาติของข้อมูลสูญหายไป (หรือไม่ชัดเจน) และมีผลทำให้การฝึกโครงข่ายประสาทเทียม เพื่อทำงานกับข้อมูลลักษณะนี้ทำได้ยากขึ้น. โครงข่ายคอนโวลูชั่น ออกแบบมาโดยเฉพาะ เพื่อรองรับข้อมูลที่มีโครงสร้างลำดับมิติ.
เพื่อลดการสับสนกับคำว่ามิติในความหมายเดิม คำว่า ลำดับมิติ หรือ ชุดมิติ หรือ ชุดลำดับมิติ หรือ ลำดับชั้น จะถูกใช้สำหรับเน้นถึงโครงสร้างที่มีลักษณะลำดับมิติ.
กลไกที่สำคัญของโครงข่ายคอนโวลูชั่นที่ใช้ประโยชน์จากลักษณะโครงสร้างมิติของข้อมูล ประกอบด้วย (1) การเชื่อมต่อท้องถิ่น (local connections), (2) การใช้ค่าน้ำหนักร่วม (shared weights), (3) การดึงรวม (pooling), (4) การใช้โครงสร้างต่อกันหลายๆชั้น (multiple layers). กลไกเหล่านี้ ดำเนินการผ่านชั้นคำนวณสองแบบ คือ ชั้นคอนโวลูชั่น (convolution layer) และ ชั้นดึงรวม (pooling layer). ชั้นคอนโวลูชั่น ทำกลไกของการเชื่อมต่อท้องถิ่น และการใช้ค่าน้ำหนักร่วม. ชั้นดึงรวม ทำกลไกการเชื่อมต่อท้องถิ่น และการดึงรวม. โครงข่ายคอนโวลูชั่น จะใช้ทั้งชั้นคอนโวลูชั่นและชั้นดึงรวม หลาย ๆ ชั้นต่อกัน และอาจใช้ชั้นคำนวณแบบดั่งเดิม ที่มักเรียกว่า ชั้นเชื่อมต่อเต็มที่ (fully connected layer) 1 (Fully Connected Layer) สำหรับคำนวณเอาต์พุตในรูปแบบที่ต้องการ.
รูป 1.2 แสดงแผนภาพเปรียบเทียบ ชั้นเชื่อมต่อเต็มที่ ชั้นเชื่อมต่อท้องถิ่น และ ชั้นเชื่อมต่อท้องถิ่นที่ใช้ค่าน้ำหนักร่วม. รูป 1.2 แสดงกรณีข้อมูลที่มีโครงสร้างหนึ่งลำดับชั้น2.
6.0.0.0.2 หมายเหตุ
แนวคิดของชั้นคอนโวลูชั้นนั้นมีความทั่วไปมากพอ ที่จะนำไปปรับใช้กับลักษณะข้อมูลที่อาจมีโครงสร้างมิติแบบต่าง ๆ ได้. แต่เพื่อความกระชับ หัวข้อนี้อภิปรายโครงข่ายคอนโวลูชั่น สำหรับข้อมูลภาพ ซึ่งมักมีโครงสร้างมิติสำหรับหนึ่งภาพคือ \(C \times H \times W\) เมื่อ \(C\) แทนจำนวนลักษณะอิสระ เช่น จำนวนช่องสี และ \(H\) กับ \(W\) แทนขนาดของชุดลำดับมิติ (ขนาดของภาพ ได้แก่ ความสูงกับความกว้าง). กรณีเช่นนี้ มักถูกเรียกว่า คอนโวลูชั่นสองมิติ (two-dimension convolution) สำหรับสองชุดมิติลำดับสัมพันธ์ ซึ่งเหมาะกับข้อมูล เช่น ภาพ. สังเกตว่า แต่ภาพ อาจแทนด้วย เทนเซอร์สามลำดับชั้น \(\boldsymbol{X} \in \mathbb{B}^{C \times H \times W}\) แต่ความสัมพันธ์เชิงลำดับมีเฉพาะชุดมิติที่สองและสาม. ชุดมิติแรก (ชุดมิติของสี) ไม่มีความสัมพันธ์เชิงลำดับ.
คอนโวลูชั่นหนึ่งมิติ (one-dimension convolution) สำหรับหนึ่งชุดมิติลำดับ จะเหมาะกับข้อมูล เช่น เสียง โดย ชุดมิติที่มีลำดับ คือ เวลา. คอนโวลูชั่นสามมิติ (three-dimension convolution) จะเหมาะกับข้อมูล เช่น วิดีโอ โดย ชุดมิติที่มีลำดับ คือ ชุดมิติพิกเซลแนวตั้ง, ชุดมิติพิกเซลแนวนอน, และชุดมิติเวลา.

6.1 ชั้นคอนโวลูชั่น
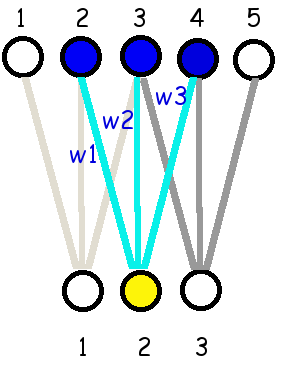
ชั้นคอนโวลูชั่น (convolution layer) เป็นชั้นคำนวณ ที่มีกลไกการเชื่อมต่อท้องถิ่น, การใช้ค่าน้ำหนักร่วม และการรักษาโครงสร้างมิติของเอาต์พุต. รูป 1.5 แสดงกลไกของการเชื่อมต่อท้องถิ่น และการใช้ค่าน้ำหนักร่วม. ค่าเอาต์พุตของชั้น \(z_i = h(a_i)\) โดย \(h(\cdot)\) แทนฟังก์ชันกระตุ้น และ คอนโวลูชั่นเอาต์พุต \(a_i = w_1 \cdot x_{i} + w_2 \cdot x_{i+1} + w_3 \cdot x_{i+2} + b\) เมื่อ \(i = 1, 2, 3\) และ \(b\) แทนค่าไบอัส (ไบอัส ไม่ได้แสดงในภาพ) เช่น \(a_1 = w_1 \cdot x_1 + w_2 \cdot x_2 + w_3 \cdot x_3 + b\) (ภาพซ้าย เน้นให้เห็นการคำนวณสำหรับ \(a_1\)), \(a_2 = w_1 \cdot x_2 + w_2 \cdot x_3 + w_3 \cdot x_4 + b\) (ภาพกลาง), และ \(a_3 = w_1 \cdot x_3 + w_2 \cdot x_4 + w_3 \cdot x_5 + b\) (ภาพขวา). สังเกตว่า (1) ค่าน้ำหนัก \(w_1\), \(w_2\), และ \(w_3\) ถูกใช้ร่วมกัน (การใช้ค่าน้ำหนักร่วม) และจำนวนค่าน้ำหนัก คือ \(3\). (2) แม้ว่าไบอัสไม่ได้แสดงในภาพ แต่ควรบันทึกไว้ว่า ค่าไบอัสก็ใช้ร่วมกัน นั่นคือ ทั้ง \(a_1, a_2, a_3\) ก็ใช้ไบอัส \(b\) ค่าเดียวกัน. (3) เอาต์พุตแต่ละตัว เชื่อมต่อกับอินพุตจำนวนจำกัด ซึ่งจำนวนจะเท่ากับจำนวนค่าน้ำหนัก (การเชื่อมต่อท้องถิ่น). (4) อินพุตขนาดเป็น \(5\) แต่เอาต์พุตมีขนาดเป็น \(3\). ถ้าใช้เอาต์พุตขนาดน้อยกว่า \(3\) จะไม่สามารถครอบคลุมอินพุตได้ครบทุกตัว. ถ้าใช้เอาต์พุตขนาดมากกว่า \(3\) เอาต์พุตตัวที่สี่ ตัวที่ห้า และตัวที่หก จะมีอินพุตไม่ครบ.
 |
 |
 |
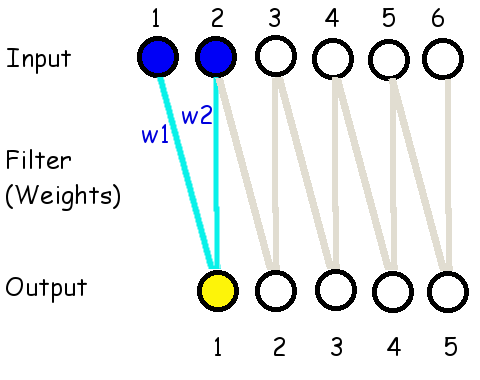
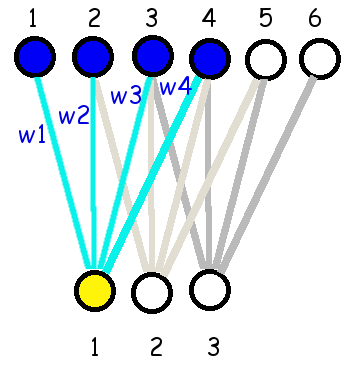
เนื่องจากประวัติการพัฒนาชั้นคอนโวลูชั่น มาจากกลุ่มงานทางด้านการประมวลผลภาพ ค่าน้ำหนักร่วมเหล่านี้ มักถูกเรียกว่า ฟิลเตอร์ (filter) หรือ เคอร์เนล (kernel). จำนวนค่าน้ำหนัก ซึ่งกำหนดขนาดของอินพุตที่เชื่อมต่อกับเอาต์พุตแต่ละตัว จะถูกเรียกเป็น ขนาดของฟิลเตอร์ (filter size). ขนาดของฟิลเตอร์เป็นพารามิเตอร์ของแบบจำลองที่ผู้ใช้เลือก. รูป 1.8 แสดงให้เห็นการเชื่อมต่อเมื่อใช้ฟิลเตอร์ขนาดต่าง ๆ. การคำนวณค่าคอนโวลูชั่นเอาต์พุตทำโดย \[\begin{eqnarray} a_k = b + \sum_{j=1}^{H_F} w_j \cdot x_{k+j-1} \label{eq: deep conv filter x of D} \end{eqnarray}\] สำหรับ \(k = 1, \ldots, H - H_F + 1\) เมื่อ \(b\) คือค่าไบอัส. ค่าคงที่ \(H_F\) คือขนาดของฟิลเตอร์. ตัวแปร \(w_j\) คือค่าน้ำหนัก. ตัวแปร \(x_i\) คืออินพุต สำหรับ \(i = 1, \ldots, H\) โดย \(H\) คือขนาดของอินพุต.
สังเกต (1) ขนาดของฟิลเตอร์ยิ่งใหญ่ การเชื่อมต่อยิ่งครอบคลุมอินพุตจำนวนมากขึ้น (2) ขนาดของเอาต์พุตลดลง เช่น อินพุตขนาด \(6\) ใช้ฟิลเตอร์ขนาด \(2\) มีเอาต์พุตขนาด \(5\), อินพุตขนาด \(6\) ใช้ฟิลเตอร์ขนาด \(3\) มีเอาต์พุตขนาด \(4\), อินพุตขนาด \(6\) ใช้ฟิลเตอร์ขนาด \(4\) มีเอาต์พุตขนาด \(3\) เป็นต้น. เมื่อพิจารณาดูจะพบว่า อินพุตขนาด \(H\) เมื่อใช้ฟิลเตอร์ขนาด \(H_F\) จะมีเอาต์พุตขนาด \(H - H_F + 1\).
หมายเหตุ วงการและศาสตร์การเรียนรู้ของเครื่อง จะเรียกกระบวนการดังสมการ \(\eqref{eq: deep conv filter x of D}\) ว่า คอนโวลูชั่น. ในขณะที่คณิตศาสตร์โดยทั่วไป และศาสตร์การประมวลผลสัญญาณ (signal processing) มักเรียกกระบวนการ เช่นนี้ ว่า สหสัมพันธ์ข้าม (cross-correlation) และใช้คำว่า คอนโวลูชั่น กับปฏิบัติการ เช่น \(a_k = \sum_j w_j \cdot x_{k-j-1}\) ซึ่งมีจุดต่างสำคัญอยู่ที่การกลับลำดับของตัวถูกดำเนินการตัวหนึ่ง. เนื่องจากค่าน้ำหนักฟิลเตอร์ที่ใช้ของศาสตร์การเรียนรู้ของเครื่อง มักได้จากกระบวนเรียนรู้ การทำหรือไม่ทำขั้นตอนการกลับลำดับ ไม่มีผลกับผลลัพธ์สุดท้าย. ดังนั้นการตัดขั้นตอนกลับลำดับออก ช่วยให้โปรแกรมซับซ้อนน้อยลง และทำงานได้เร็วขึ้น.
 |
 |
 |
6.1.0.0.1 การเติมเต็มด้วยศูนย์.
ในทางปฏิบัติ เทคนิคการเติมเต็ม (padding) หรือเรียกว่า การเติมเต็มด้วยศูนย์ (zero-padding) มักถูกนำมาใช้ เพื่อรักษาขนาดของเอาต์พุตให้เท่ากับขนาดของอินพุต (เช่น รักษาขนาดภาพของเอาต์พุต ให้เท่ากับขนาดภาพของอินพุต). นั่นคือ เมื่อใช้ฟิลเตอร์ขนาด \(H_F\) อินพุต \(\boldsymbol{x}\) ขนาด \(H\) จะถูกขยายเป็น \(\boldsymbol{\hat{x}}\) ขนาด \(H + H_F - 1\) โดยเพิ่มค่า \(0\) เข้าไปจนเต็มขนาด. ตัวอย่างเช่น \(H_F = 3\), \(\boldsymbol{x} = \{x_1, x_2, x_3, x_4, x_5, x_6\}\) (ขนาด \(H = 6\)) จะถูกขยายเป็น \(\boldsymbol{\hat{x}} = \{0, x_1, x_2, x_3, x_4, x_5, x_6, 0\}\) ขนาดเพิ่มเป็น \(6 + 3 - 1 = 8\). นั่นคือ เพิ่มศูนย์ \(2\) ตัว. หรือเมื่อใช้ฟิลเตอร์ขนาด \(H_F = 5\), อินพุต \(\boldsymbol{x} = \{x_1, x_2, x_3, x_4, x_5, x_6\}\) (ขนาด \(H = 6\)) จะถูกขยายเป็น \(\boldsymbol{\hat{x}} = \{0, 0, x_1, x_2, x_3, x_4, x_5, x_6, 0, 0\}\) ขนาดเพิ่มเป็น \(6 + 5 - 1 = 10\). นั่นคือ เพิ่มศูนย์ \(4\) ตัว.
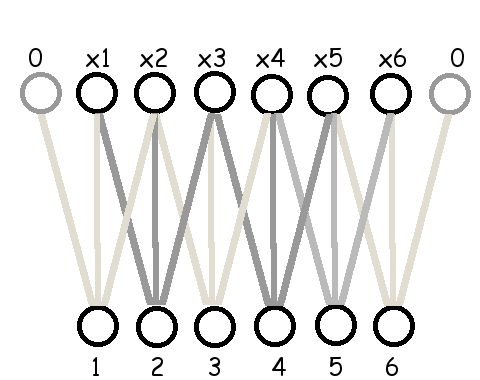
ขนาดของฟิลเตอร์ มักถูกนิยมเลือกให้เป็นเลขคี่. ขนาดของฟิลเตอร์เป็นเลขคี่ ทำให้การเติมเต็มด้วยศูนย์ สามารถเติมได้อย่างสมดุลย์ทั้งสองปลาย3. ขนาดของฟิลเตอร์เป็นเลขคู่ก็สามารถทำได้ เพียงแต่จะมีปลายด้านหนึ่งที่จะถูกเติมมากกว่าอีกด้านเท่านั้น. รูป 1.9 แสดงแผนภาพการเชื่อมต่อ เมื่อทำการเติมเต็มด้วยศูนย์. ในภาพ ขนาดของฟิลเตอร์เป็น \(3\) ดังนั้นต้องเติมศูนย์ \(H_F - 1 = 2\) ตำแหน่ง โดยกระจายการเติมไปทั้งสองปลาย. เมื่อมีการเติมเต็ม การคำนวณค่าคอนโวลูชั่นเอาต์พุตทำโดย \[\begin{eqnarray} a_k = b + \sum_{j=1}^{H_F} w_j \cdot \hat{x}_{k+j-1} \label{eq: deep conv filter x of D padding} \end{eqnarray}\] สำหรับ \(k = 1, \ldots, H\) และ \(\hat{x}_i\) คืออินพุตที่ถูกเติมเต็มด้วยศูนย์ สำหรับ \(i = 1, \ldots, H + H_F - 1\) โดย \(H\) คือขนาดของอินพุตเดิม. สำหรับกรณีขนาดฟิลเตอร์เป็นเลขคี่ (\(H_F \; \mathrm{mod} \; 2 = 1\)) \[\begin{eqnarray} \hat{x}_i = \left\{ \begin{array}{l l} 0, & \mbox{ สำหรับ } i \leq \frac{H_F-1}{2} \mbox{ หรือ } i > \frac{H_F-1}{2} + H,\\ x_{i - (H_F-1)/2} , & \mbox{ นอกเหนือจากข้างต้น}. \end{array} \right. \label{eq: deep padding} \end{eqnarray}\] โดย \(i = 1, \ldots, H + H_F - 1\).
6.1.0.0.2 ขนาดก้าวย่าง.
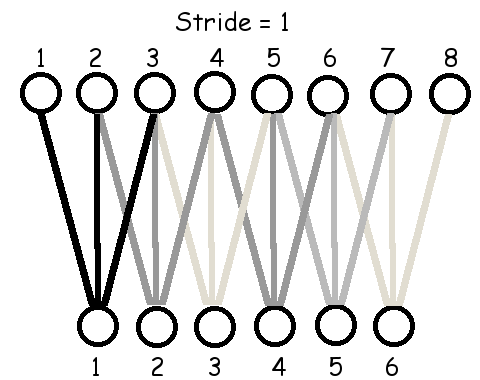
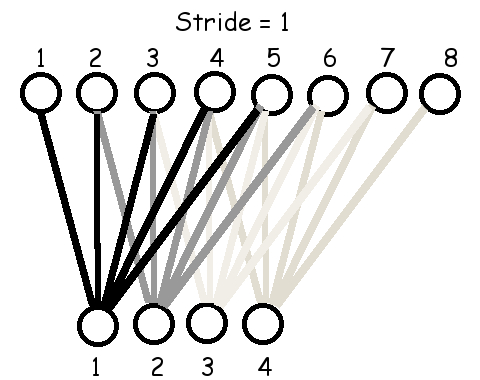
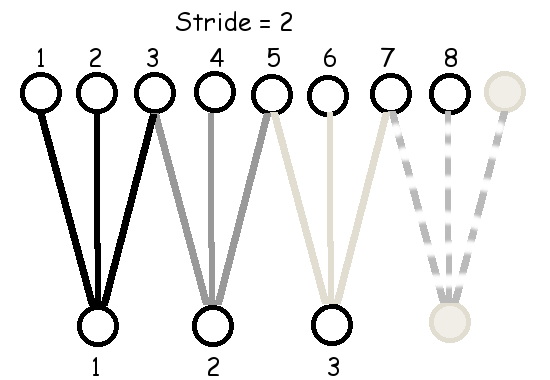
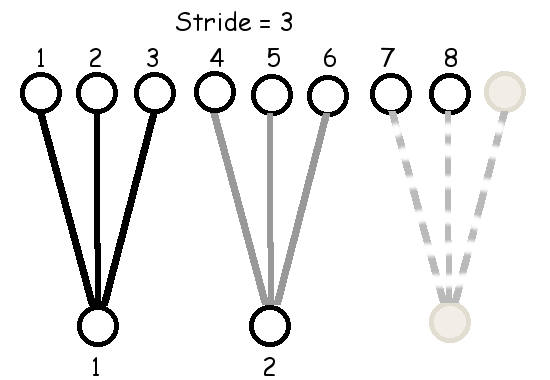
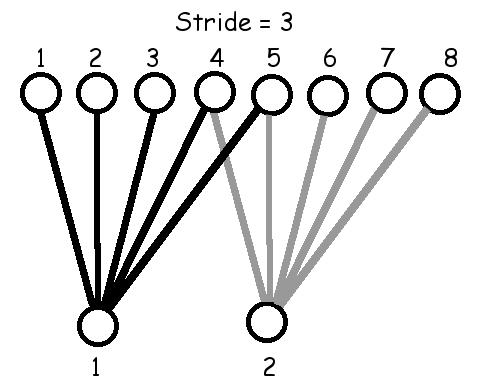
ตัวอย่างข้างต้น เอาต์พุตแต่ละหน่วยจะรับอินพุตต่างจากเอาต์พุตหน่วยข้าง ๆ โดยขยับลำดับอินพุตไปแค่หนึ่งตำแหน่ง. การขยับตำแหน่งของอินพุตสำหรับเอาต์พุตหน่วยข้าง ๆ กันนี้ ไม่จำเป็นต้องจำกัดเพียง \(1\) ตำแหน่งเท่านั้น. การขยับตำแหน่งนี้ สามารถทำทีละหลาย ๆ ตำแหน่ง และการขยับตำแหน่งของเอาต์พุตหน่วยข้าง ๆ กันนี้ จะเรียกว่า ขนาดก้าวย่าง (stride). รูป 1.15 แสดงการเชื่อมต่อ เมื่อใช้ฟิลเตอร์ขนาด \(3\) และ \(5\) กับขนาดก้าวย่างต่าง ๆ.
| Filter Size 3 | Filter Size 5 |
 |
 |
 |
 |
 |
 |
หากอินพุตที่เติมมีขนาด \(\hat{H}\) และฟิลเตอร์มีขนาด \(H_F\) และก้าวย่างมีขนาด \(S\) แล้วขนาดของเอาต์พุต \(H'\) คำนวณได้จาก \[\begin{eqnarray} H' = \left\lfloor \frac{\hat{H} - H_F}{S} \right\rfloor + 1 \label{eq: deep size of conv output} \end{eqnarray}\]
ดังนั้น หากต้องการทำการเติมเต็ม เพื่อให้ได้ขนาดของเอาต์พุตที่ต้องการ \(\hat{H}'\) เราสามารถคำนวณขนาดของอินพุตหลังเติมเต็ม \(\hat{H}\) ได้จาก \[\begin{eqnarray} \hat{H} = S \cdot (\hat{H}' - 1) + H_F \label{eq: deep size of padded input} \end{eqnarray}\] และ จำนวนของศูนย์ที่ต้องเติมใส่อินพุตจะเท่ากับ \(\hat{H} - H\).
นั่นคือ หากต้องการเติมเต็ม เพื่อให้ได้ขนาดเอาต์พุตเท่ากับขนาดอินพุตเดิม \(\hat{H}' = H\) จะได้ว่า จำนวนของศูนย์ที่ต้องเติมใส่อินพุตจะเท่ากับ \(S \cdot (H - 1) + H_F - H\). หรือ หากต้องการเติมเต็ม เพื่อให้ได้ขนาดเอาต์พุต \(\hat{H}' = \left\lceil \frac{H}{S} \right\rceil\) จะได้ว่า จำนวนของศูนย์ที่ต้องเติมใส่อินพุตจะเท่ากับ \(S \cdot (\left\lceil \frac{H}{S} \right\rceil - 1) + H_F - H\).
ตัวอย่างเช่น อินพุตขนาด \(H = 6\) ใช้ฟิลเตอร์ขนาด \(H_F = 3\) ใช้ขนาดย่างก้าว \(S = 1\) และต้องการให้ขนาดเอาต์พุตเท่ากับขนาดอินพุตเดิม จะได้ \(\hat{H} = 1 \cdot (6 - 1) + 3 = 8\) และต้องเติมศูนย์ \(2\) ตัว. อินพุตขนาด \(H = 6\) ใช้ฟิลเตอร์ขนาด \(H_F = 3\) ใช้ขนาดย่างก้าว \(S = 2\) และต้องการให้ขนาดเอาต์พุตเท่ากับขนาดอินพุตเดิม จะได้ \(\hat{H} = 2 \cdot (6 - 1) + 3 = 13\) และต้องเติมศูนย์ \(7\) ตัว. อินพุตขนาด \(H = 8\) ใช้ฟิลเตอร์ขนาด \(H_F = 5\) ใช้ขนาดย่างก้าว \(S = 3\) และต้องการให้ขนาดเอาต์พุตเท่ากับขนาดอินพุตเดิม จะได้ \(\hat{H} = 3 \cdot (8 - 1) + 5 = 26\) และต้องเติมศูนย์ \(18\) ตัว.
ชั้นคอนโวลูชั่น ที่มีอินพุต \(\boldsymbol{x} \in \mathbb{R}^H\) ใช้ฟิลเตอร์ \(\boldsymbol{w} \in \mathbb{R}^{H_F}\) มีขนาดก้าวย่างเป็น \(S\) และทำการเติมเต็มด้วยศูนย์เพื่อให้เอาต์พุต \(\boldsymbol{a}\) มีขนาด \(H\) สามารถคำนวณค่าคอนโวลูชั่นเอาต์พุตแต่ละค่า ได้จาก \[\begin{eqnarray} a_k = b + \sum_{j=1}^{H_F} w_j \cdot \hat{x}_{S \cdot (k-1)+j} \label{eq: deep conv simple conv} \end{eqnarray}\] เมื่อ \(k = 1, \ldots, H\) และ \(b\) แทนค่าไบอัส. สังเกตว่า \(\boldsymbol{a}\) รักษาโครงสร้างมิติของ \(\boldsymbol{x}\) ไว้. อินพุต \(\boldsymbol{x}\) มีลำดับมิติเดียว คอนโวลูชั่นเอาต์พุต \(\boldsymbol{a}\) ก็มีลำดับมิติเดียว.
กรณีที่อภิปรายมาข้างต้น โครงสร้างมิติของอินพุตไม่ได้ซับซ้อน นั่นคือมีเพียงลำดับมิติเดียว. ปัจจัยที่สำคัญต่อมาของชั้นคอนโวลูชั่น คือ กลไกที่ชัดเจนในการจัดการกับอินพุตที่มีโครงสร้างมิติที่ซับซ้อน และการยอมใหเอาตพุตรักษาโครงสรางเชิงมิติบางสวนของอินพุตไวได.
รูป 1.16 เปรียบเทียบโครงสร้างมิติเชิงเดี่ยว (ภาพซ้าย) กับโครงสร้างมิติที่มี \(2\) ชุดลำดับ (ภาพกลาง) และตัวอย่างเชิงตัวเลข (ภาพขวา). จากตัวอย่างเชิงเลขในรูปจะเห็นว่า
| เอาต์พุต \(a_{1,1}\) | \(= 2.7\) | \(+ (1) \cdot 89 + (2) \cdot 84 + (1.5) \cdot 105\) |
| \(+ (2.5) \cdot 6 + (8) \cdot 0 + (2.3) \cdot 4\) | ||
| \(+ (1.6) \cdot 13 + (1.8) \cdot 52 + (1.4) \cdot 57\) | ||
| \(= 635.6\) | ||
| ซึ่งเอาต์พุตตำแหน่ง \((1,1)\) ถูกเน้นในภาพขวา. | ||
| เอาต์พุต \(a_{1,2}\) | \(= 2.7\) | \(+ (1) \cdot 84 + (2) \cdot 105 + (1.5) \cdot 116\) |
| \(+ (2.5) \cdot 0 + (8) \cdot 4 + (2.3) \cdot 20\) | ||
| \(+ (1.6) \cdot 52 + (1.8) \cdot 57 + (1.4) \cdot 14\) | ||
| \(= 754.1\) | ||
| \(\ldots\) | ||
| เอาต์พุต \(a_{2,1}\) | \(= 2.7\) | \(+ (1) \cdot 6 + (2) \cdot 0 + (1.5) \cdot 4\) |
| \(+ (2.5) \cdot 13 + (8) \cdot 52 + (2.3) \cdot 57\) | ||
| \(+ (1.6) \cdot 50 + (1.8) \cdot 58 + (1.4) \cdot 60\) | ||
| \(= 862.7\) | ||
| เป็นต้น. | ||
สังเกตว่า (1) รูป 1.16 ไม่มีการทำการเติมเต็มด้วยศูนย์. (2) ขนาดก้าวย่างเป็น \(1 \times 1\). นั่นคือ ขยับตามแนวตั้งทีละหนึ่งหน่วยอินพุต (พิกเซล) และขยับตามแนวนอนก็ทีละหนึ่งหน่วยอินพุต. (3) คอนโวลูชั่นเอาต์พุตมี \(2\) ลำดับมิติ เช่นเดียวกับอินพุต แม้จะขนาดเล็กกว่า เพราะไม่ได้ทำการเติมเต็ม. และ เพื่อเน้นถึงโครงสร้างมิติที่รักษาไว้นี้ คอนโวลูชั่นเอาต์พุต อาจจะถูกเรียกว่า แผนที่คอนโวลูชั่น (convolution map) เพื่อกันการสับสนกับเอาต์พุตสุดท้ายของโครงข่ายทั้งหมด ซึ่งเอาต์พุตสุดท้าย คือ เอาต์พุตของชั้นสุดท้ายของโครงข่าย.
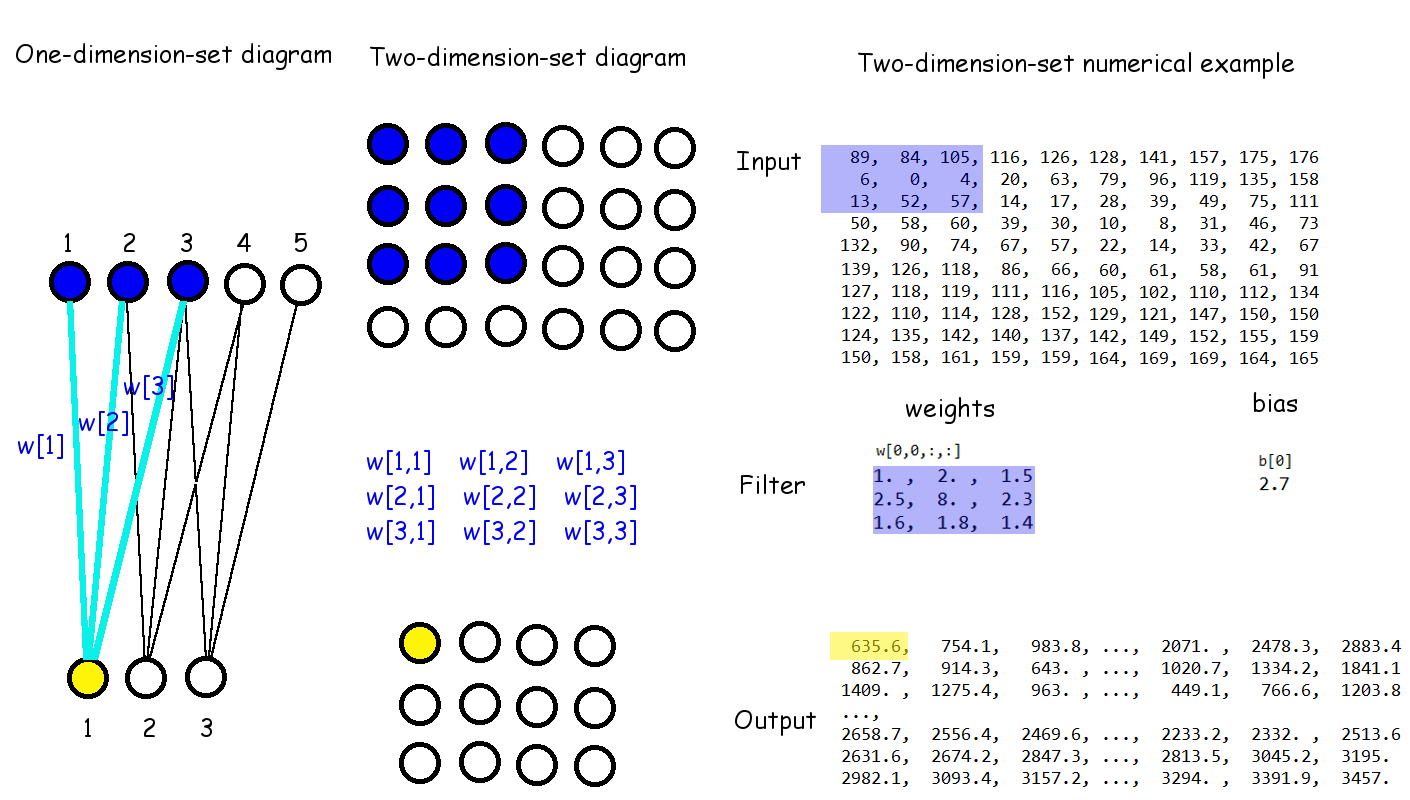
นั่นคือ เมื่ออินพุต \(\boldsymbol{X} \in \mathbb{R}^{H \times W}\) และเลือกใช้ฟิลเตอร์ขนาด \(H_F \times W_F\) ซึ่งหมายถึง \(\boldsymbol{W} \in \mathbb{R}^{H_F \times W_F}\) และเลือกก้าวย่างขนาด \(S_H \times S_W\) แล้ว (ทำนองเดียวกับสมการ \(\eqref{eq: deep conv simple conv}\)) คอนโวลูชั่นเอาต์พุต \(\boldsymbol{A} \in \mathbb{R}^{H \times W}\) สามารถคำนวณได้จาก \[\begin{eqnarray} a_{k,l} = b + \sum_{i=1}^{H_F} \sum_{j=1}^{H_W} w_{ij} \cdot \hat{x}_{S_H \cdot (k-1)+i, S_W \cdot (l-1)+j} \label{eq: deep conv conv HxW} \end{eqnarray}\] \(k = 1, \ldots, H\), \(l = 1, \ldots, W\) โดย \(\hat{x}\) คืออินพุตที่ผ่านการเติมเต็ม และ \(b\) คือไบอัส.
อย่างไรก็ตาม เมื่อพิจารณารูป 1.1 จะเห็นว่า ข้อมูลภาพสีหนึ่งภาพมีโครงสร้างมิติเป็น \(3\) ชุดมิติ ได้แก่ ชุดสำหรับช่องสีขนาด \(3\), ชุดลำดับแนวตั้งขนาด \(133\) และชุดลำดับสำหรับแนวนอนขนาด \(175\). นั่นคือ มีอินพุต \(\boldsymbol{X} \in \mathbb{R}^{C \times H \times W}\). โดยทั่วไป ชั้นคอนโวลูชั่น จะเลือกจัดการกับชุดมิติช่องสีเป็นเสมือนชุดมิติที่ไม่มีลำดับ แต่ชุดลำดับแนวตั้งและแนวนอนแบบชุดมิติมีลำดับ. การคำนวณคอนโวลูชั่นเอาต์พุต \(\boldsymbol{A} \in \mathbb{R}^{H \times W}\) สำหรับกรณีนี้ (โครงสร้างมีชุดมิติที่มีลำดับ และไม่มีลำดับ) จะทำดังสมการ \(\eqref{eq: deep conv conv CxHxW}\)
\[\begin{eqnarray} a_{k,l} = b + \sum_{c=1}^C \sum_{i=1}^{H_F} \sum_{j=1}^{H_W} w_{cij} \cdot \hat{x}_{c, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j} \label{eq: deep conv conv CxHxW} \end{eqnarray}\] \(k = 1, \ldots, H\) และ \(l = 1, \ldots, W\) เมื่อเลือกใช้ฟิลเตอร์ขนาด \(H_F \times W_F\) ซึ่งหมายถึง \(\boldsymbol{W} \in \mathbb{R}^{C \times H_F \times W_F}\) เพราะ ชุดมิติแรกของฟิลเตอร์จะต้องมีขนาดเท่ากับขนาดชุดมิติที่ไม่มีลำดับของอินพุต, ก้าวย่างขนาด \(S_H \times S_W\), และ \(\hat{x}\) คืออินพุตที่ผ่านการเติมเต็ม.
รูป 1.17 แสดงการคำนวณคอนโวลูชั่น เมื่ออินพุตมีโครงสร้าง \(3\) ชุดมิติ โดยชุดมิติแรกไม่มีลำดับ. รูปเน้นให้เห็นความสัมพันธ์ระหว่างเอาต์พุต \(a_{1,2}\) ที่เชื่อมโยงกับ อินพุต \(x_{1,1,2}, \ldots x_{1,3,4}\) (ช่องสีน้ำเงิน), \(x_{2,1,2}, \ldots\) \(x_{2,3,4}\) (ช่องสีเขียว), \(x_{3,1,2}, \ldots x_{3,3,4}\) (ช่องสีแดง) ดังที่เน้นคำในภาพ. จากตัวอย่างเชิงเลขในรูปจะเห็นว่า
| เอาต์พุต \(a_{1,2}\) | \(= 2.7\) | (ไบอัส) |
| \(+ (1) \cdot 84 + (2) \cdot 105 + (1.5) \cdot 116\) | ||
| \(+ (2.5) \cdot 0 + (8) \cdot 4 + (2.3) \cdot 20\) | ||
| \(+ (1.6) \cdot 52 + (1.8) \cdot 57 + (1.4) \cdot 14\) | (ช่องสีน้ำเงิน รวม \(751.4\)) | |
| \(+ (1.3) \cdot 90 + (2.1) \cdot 113 + (1.7) \cdot 124\) | ||
| \(+ (2.2) \cdot 3 + (6.4) \cdot 11 + (3.2) \cdot 29\) | ||
| \(+ (1.5) \cdot 60 + (2.1) \cdot 65 + (1.1) \cdot 24\) | (ช่องสีเขียว รวม \(987.8\)) |
| \(+ (0.8) \cdot 103 + (1) \cdot 126 + (0.6) \cdot 137\) | ||
| \(+ (0.9) \cdot 18 + (2.3) \cdot 26 + (1.3) \cdot 43\) | ||
| \(+ (0.4) \cdot 77 + (0.8) \cdot 82 + (0.2) \cdot 41\) | (ช่องสีแดง รวม \(527.1\)) | |
| \(= 2269.0\) | ||
| เป็นต้น. | ||
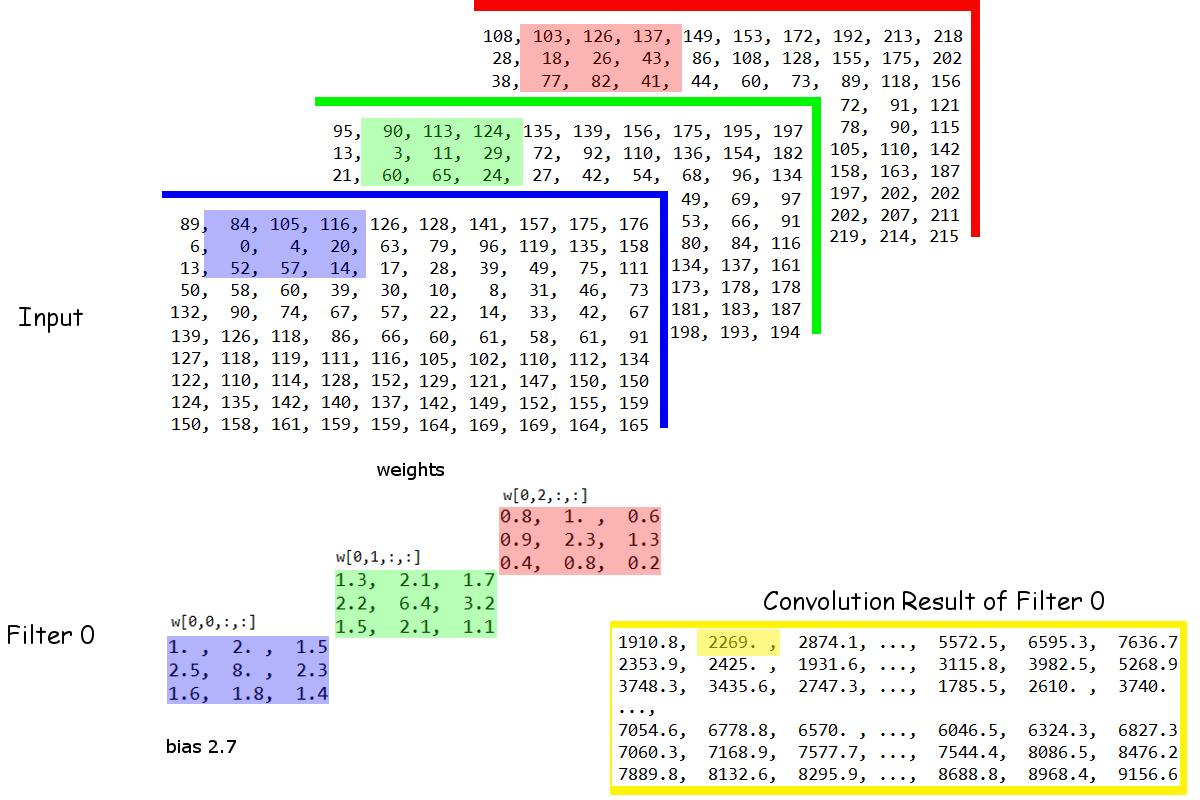
กลไกของคอนโวลูชั่นที่กล่าวมา เป็นเพียงการคำนวณค่าของคอนโวลูชั่นเอาต์พุต การใช้งานชั้นคอนโวลูชั่นในโครงข่ายแบบลึกนั้น หลังจากทำการคำนวณคอนโวลูชั่น (ผลรวมเชิงเส้นระหว่างอินพุตกับค่าน้ำหนัก) แล้ว ค่าที่ได้จะนำไปผ่านฟังก์ชันกระตุ้น เพื่อให้ได้ผลลัพธ์ของชั้นคอนโวลูชั่น ดังแสดงในสมการ \(\eqref{eq: deep conv output}\), \[\begin{eqnarray} z_{k,l} = h(a_{k,l}) \label{eq: deep conv output} \end{eqnarray}\] เมื่อ \(h(\cdot)\) คือฟังก์ชันการกระตุ้น (เช่น เรคติไฟด์ลิเนียร์, สมการ \(\eqref{eq: deep rectified linear}\)) และ \(a_{k,l}\) คือคอนโวลูชั่นเอาต์พุต (สมการ \(\eqref{eq: deep conv conv CxHxW}\)). เอาต์พุต \(\boldsymbol{Z} \in \mathbb{R}^{H \times W}\) นี้ อาจถูกเรียกว่า แผนที่ลักษณะสำคัญ (feature map).
การใช้กลไกของการเชื่อมต่อท้องถิ่น ร่วมกับการใช้ค่าน้ำหนักร่วม จะเปรียบเสมือนการทำเทคนิคหน้าต่างเลื่อน(หัวข้อ [sec: sliding window]) เพื่อค้นหารูปแบบ ที่อาจปรากฏอยู่ตำแหน่งต่าง ๆ ในอินพุตได้. นั่นคือ เหมือนกับการเลื่อนฟิลเตอร์ (เทียบเท่ากับหน้าต่าง) ไปตำแหน่งต่าง ๆ ของอินพุต เพื่อค้นหารูปแบบลักษณะที่สำคัญ. การใช้ฟิลเตอร์หนึ่งตัว ก็เปรียบเสมือน รูปแบบของลักษณะสำคัญหนึ่งรูปแบบ. การใช้งานโครงข่ายคอนโวลูชั่น ในทางปฏิบัติ จะใช้ฟิลเตอร์หลาย ๆ ตัว ซึ่งเปรียบเสมือน การค้นหารูปแบบของลักษณะสำคัญหลาย ๆ รูปแบบ และ ผลลัพธ์ ก็จะได้แผนที่ลักษณะสำคัญหลาย ๆ แผนที่.
ทบทวนการคำนวณชั้นคอนโวลูชั่น สำหรับอินพุต \(\boldsymbol{X} \in \mathbb{R}^{C \times H \times W}\) และฟิลเตอร์ขนาด \(H_F \times W_F\) ทั้งหมด \(F\) ตัว นั่นคือ \(\boldsymbol{W} \in \mathbb{R}^{F \times C \times H_F \times W_F}\) แล้วเอาต์พุต \(\boldsymbol{Z} \in \mathbb{R}^{F \times H \times W}\) หาได้จาก \[\begin{eqnarray} a_{f,k,l} &=& b_f + \sum_{c=1}^C \sum_{i=1}^{H_F} \sum_{j=1}^{W_F} w_{fcij} \cdot \hat{x}_{c, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j} \label{eq: deep conv conv FxCxHxW} \\ z_{f,k,l} &=& h(a_{f,k,l}) \label{eq: deep conv 2Dconv Output} \end{eqnarray}\] \(f = 1, \ldots, F\), \(k = 1, \ldots, H\) และ \(l = 1, \ldots, W\) เมื่อ \(S_H\), \(S_W\) คือขนาดก้าวย่าง ตามแนวตั้งและนอน ตามลำดับ. ฟังก์ชัน \(h(\cdot)\) คือ ฟังก์ชันกระตุ้น, ตัวแปร \(b_f\) คือไบอัสร่วมของฟิลเตอร์ \(f\) ส่วนตัวแปร \(\hat{x}\) คืออินพุตที่ผ่านการเติมเต็ม.
รูป 1.18 แสดงแผนภาพโครงสร้างมิติของอินพุต ฟิลเตอร์ และเอาต์พุต ของชั้นคอนโวลูชั่น. ในรูป ใช้ \(5\) ฟิลเตอร์ และผลลัพธ์ก็จะได้แผนที่ลักษณะ \(5\) แผนที่. แต่ละแผนที่ระบุการตอบสนองต่อรูปแบบสำคัญที่ตำแหน่งต่าง ๆ สำหรับแต่ละรูปแบบสำคัญ. สังเกตว่าเอาต์พุตของชั้นคอนโวลูชั่น \(\boldsymbol{Z} \in \mathbb{R}^{F \times H' \times W'}\) ซึ่งมีโครงสร้างมิติเป็น \(3\) ชุด โดยชุดแรกไม่มีลำดับ สองชุดหลังเป็นชุดลำดับที่สัมพันธ์กัน เช่นเดียวกับอินพุต ดังนั้น เอาต์พุตจากชั้นคอนโวลูชั่นชั้นหนึ่ง สามารถส่งต่อไปเป็นอีกชั้นหนึ่งได้เลย โดยไม่ต้องมีการดัดแปลงใด ๆ.
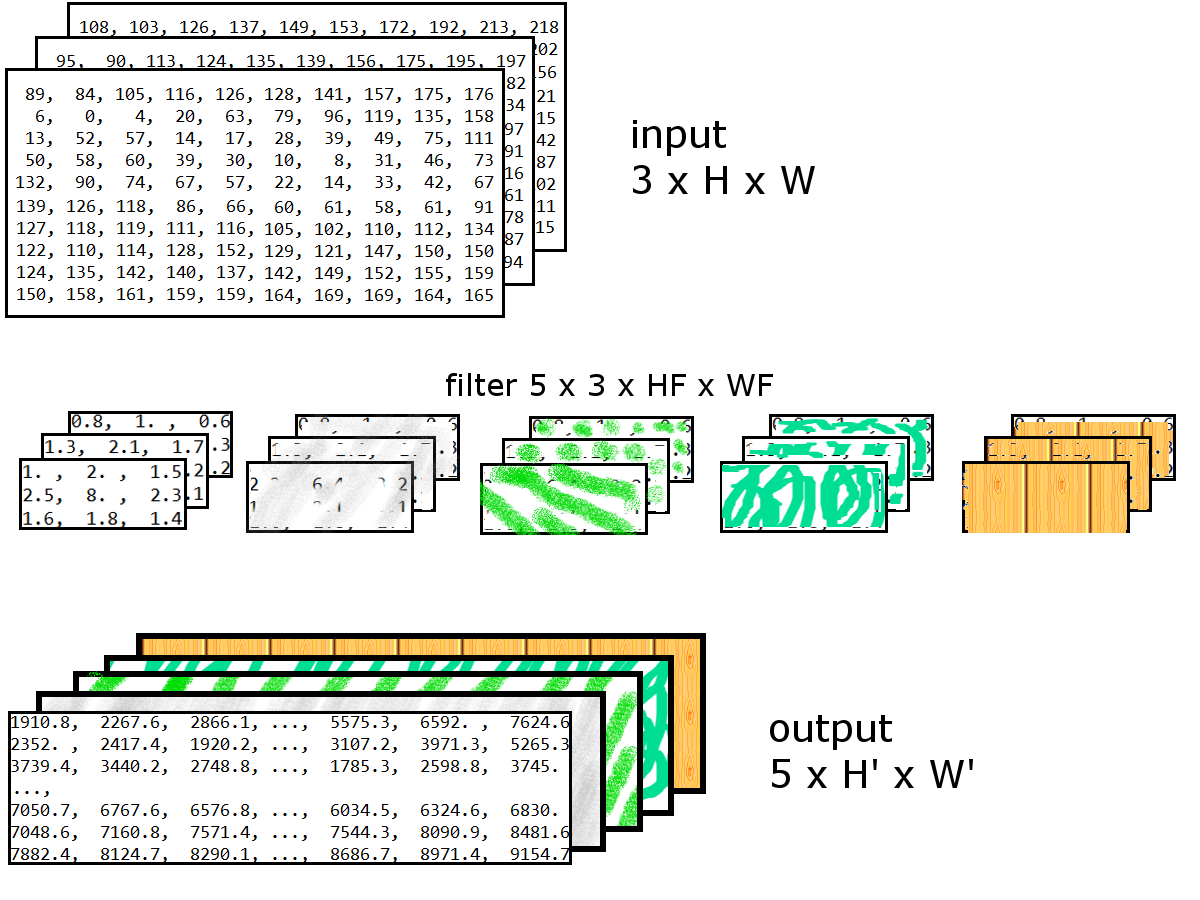
6.1.0.0.3 สนามรับรู้.
สนามรับรู้ (receptive field) สำหรับโครงข่ายคอนโวลูชั่น คือบริเวณพื้นที่ท้องถิ่นของอินพุต ที่หน่วยย่อยที่สนใจครอบคลุมถึง. ขนาดของสนามรับรู้ สามารถคำนวณได้จาก \[\begin{eqnarray} R_k = 1 + \sum_{j=1}^k (F_j - 1) \prod_{i=0}^{j-1} S_i \label{eq: receptive field} \end{eqnarray}\] เมื่อ \(R_k\) เป็นขนาดของสนามรับรู้ แล้ว \(F_j\) เป็นขนาดฟิลเตอร์ของชั้นที่ \(j\) และ \(S_i\) เป็นขนาดก้าวย่างของชั้นที่ \(i\) และกำหนดให้ \(S_0 = 1\).
ตัวอย่างเช่น โครงข่ายคอนโวลูชั่นสองชั้น ที่ชั้นแรกใช้ฟิลเตอร์ขนาด \(3 \times 3\) ก้างย่างเป็น \(1\) และชั้นที่สองก็ใช้ฟิลเตอร์ \(3 \times 3\) และก้าวย่างเป็น \(1\) แล้ว แต่ละหน่วยย่อยในชั้นที่สอง จะครอบคลุมพื้นที่ขนาด \(3 \times 3\) ในชั้นที่หนึ่ง และจะครอบคลุมพื้นที่ขนาด \(5 \times 5\) ของอินพุต. นั่นคือ \(R_2 = 1 + (F_2 - 1) S_0 \cdot S_1 + (F_1 - 1) S_0\) = \(1 + (2)(1)(1) + (2)(1) = 5\).
6.2 ชั้นดึงรวม
ชั้นดึงรวม (pooling layer) ถูกนำมาใช้สำหรับ (1) การทำซับแซมปลิง (subsampling) เพื่อลดจำนวนข้อมูลลง และ (2) การสรุปลักษณะสำคัญในระแวกใกล้เคียง. กลไกการทำงานของชั้นดึงรวมจะคล้ายกับชั้นคอนโวลูชั่นที่จะขยับไปทีละก้าวย่าง เพื่อประมวลผลอินพุตในบริเวณจำกัด (การเชื่อมต่อท้องถิ่น) แต่การประมวลของชั้นดึงรวมจะแยกมิติที่ไม่มีลำดับออกจากกัน ไม่นำมาประมวลผลรวมกัน. นั่นคือ อินพุต \(\boldsymbol{X} \in \mathbb{R}^{C \times H \times W}\) โดย \(C\) คือชุดมิติที่ไม่มีลำดับ และ \(H\) และ \(W\) คือชุดมิติที่มีลำดับสัมพันธ์. เอาต์พุตของชั้นดึงรวม \(\boldsymbol{Z} \in \mathbb{R}^{C \times H' \times W'}\) สามารถคำนวณได้ดังนี้ \[\begin{eqnarray} z_{c,k,l} &=& g( \{ \hat{x}_{c, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j} \}_{i=1,\ldots, H_F, j=1,\ldots, W_F} ) \label{eq: deep conv pooling} \end{eqnarray}\] \(c = 1, \ldots, C\), \(k = 1, \ldots, H'\) และ \(l = 1, \ldots, W'\) เมื่อ \(S_H\), \(S_W\) คือขนาดก้าวย่าง ตามแนวตั้งและนอน ตามลำดับ, \(g(\cdot)\) คือ ฟังก์ชันดึงรวม, และ \(\hat{x}\) คืออินพุตที่ผ่านการเติมเต็ม เพื่อให้เอาต์พุตครอบคลุมอินพุตทุกตัว. สังเกตว่า การดึงรวมจะไม่ยุบชุดมิติอิสระ \(C\). เอาต์พุตที่ได้ยังคงมีขนาด \(C\) สำหรับชุดมิติแรกเช่นเดิม.
การทำการเติมเต็มสำหรับชั้นดึงรวม จะมีจุดประสงค์ต่างจากสำหรับชั้นคอนโวลูชั่น ตรงที่ ชั้นดึงรวมไม่ต้องการรักษาขนาดชุดมิติของอินพุตไว้ ชั้นดึงรวมต้องการลดขนาดชุดมิติลำดับนี้ลง (\(H' < H\) และ \(W' < W\)) แต่การเติมเต็มสำหรับชั้นดึงรวม ทำเพื่อให้เอาต์พุตสามารถครอบคลุมอินพุตได้ทุกตัว. ตัวอย่างเช่น ชั้นดึงรวมแบบมากที่สุด (max-pooling Layer) ขนาด \(5 \times 5\) ใช้ก้าวย่างขนาด \(2 \times 2\) หากอินพุต \(\boldsymbol{X}\) มีขนาด \(3 \times 60 \times 80\) จะพบว่า หากไม่ทำการเติมเต็ม อินพุตตัวสุดท้ายของแต่ละชุดมิติอิสระ \(\{x_{1,60,80}, x_{2,60,80},\) \(x_{3,60,80} \}\) จะถูกรับผิดชอบโดยเอาต์พุต ที่ตำแหน่ง \((29, 39)\) ซึ่ง (จากสมการ \(\eqref{eq: deep conv pooling}\)), \[\begin{eqnarray} z_{c,29,39} &=& \max \{ \hat{x}_{c, 56+i, 76+j} \}_{i=1,\ldots, 5, j=1,\ldots, 5} \nonumber \\ &=& \max \left\{ \begin{array}{lllll} \hat{x}_{c, 57, 77}, & \hat{x}_{c, 57, 78}, & \hat{x}_{c, 57, 79}, & \hat{x}_{c, 57, 80}, & \hat{x}_{c, 57, 81}, \\ \hat{x}_{c, 58, 77}, & \hat{x}_{c, 58, 78}, & \hat{x}_{c, 58, 79}, & \hat{x}_{c, 58, 80}, & \hat{x}_{c, 58, 81}, \\ \hat{x}_{c, 59, 77}, & \hat{x}_{c, 59, 78}, & \hat{x}_{c, 59, 79}, & \hat{x}_{c, 59, 80}, & \hat{x}_{c, 59, 81}, \\ \hat{x}_{c, 60, 77}, & \hat{x}_{c, 60, 78}, & \hat{x}_{c, 60, 79}, & \hat{x}_{c, 60, 80}, & \hat{x}_{c, 60, 81}, \\ \hat{x}_{c, 61, 77}, & \hat{x}_{c, 61, 78}, & \hat{x}_{c, 61, 79}, & \hat{x}_{c, 61, 80}, & \hat{x}_{c, 61, 81} \end{array} \right\} \nonumber , \end{eqnarray}\] \(c = 1, 2, 3\) ต้องการค่าอินพุตที่ตำแหน่งแนวตั้งที่ 61 และตำแหน่งแนวนอนที่ 81 ซึ่งอินพุตดั้งเดิมนั้นไม่มี. ดังนั้น \(\boldsymbol{\hat{x}}\) จึงต้องมีการเติมเต็มในตำแหน่งดังกล่าว เพื่อให้การดึงรวมสามารถครอบคลุมอินพุตดั้งเดิมได้ทั้งหมด.
แต่หากว่าการดึงรวมสามารถครอบคลุมอินพุตดั้งเดิมได้ทั้งหมดแล้วก็ไม่จำเป็นต้องมีการเติมเต็ม. ตัวอย่างเช่น ชั้นดึงรวมแบบมากที่สุด ขนาด \(3 \times 3\) ใช้ก้าวย่างขนาด \(3 \times 3\) (ไม่มีการซ้อนทับ) หากอินพุต \(\boldsymbol{X}\) มีขนาด \(3 \times 90 \times 120\) จะพบว่า แม้ไม่ทำการเติมเต็ม อินพุตตัวสุดท้ายของแต่ละชุดมิติอิสระ \(\{x_{1,90,120},\) \(x_{2,90,120}, x_{3,90,120} \}\) จะถูกรับผิดชอบโดยเอาต์พุต ที่ตำแหน่ง \((30, 40)\) พอดี โดยไม่ต้องการการเติมเต็มเพิ่ม, \[\begin{eqnarray} z_{c,30,40} &=& \max \{ \hat{x}_{c, 87+i, 3 \cdot 117+j} \}_{i=1,\ldots, 3, j=1,\ldots, 3} \nonumber \\ &=& \max \left\{ \begin{array}{lllll} \hat{x}_{c, 88, 118}, & \hat{x}_{c, 88, 119}, & \hat{x}_{c, 88, 120}, \\ \hat{x}_{c, 89, 118}, & \hat{x}_{c, 89, 119}, & \hat{x}_{c, 89, 120}, \\ \hat{x}_{c, 90, 118}, & \hat{x}_{c, 90, 119}, & \hat{x}_{c, 90, 120} \end{array} \right\} \nonumber . \end{eqnarray}\] นั่นคือ หาก \((H - H_F) \;\mathrm{ mod }\; S_H = 0\) และ \((W - W_F) \;\mathrm{ mod }\; S_W = 0\) ก็ไม่จำเป็นต้องทำการเติมเต็ม.
เมื่อทำเติมเต็มตามความจำเป็น เพื่อให้การดึงรวมครอบคลุมอินพุตทุกหน่วยแล้ว ขนาดของเอาต์พุต (หรืออาจเรียกว่า แผนที่เอาต์พุต เพื่อเน้นโครงสร้างเชิงมิติ \(2\) ชุดลำดับที่สัมพันธ์กัน) จะเป็น \(H' \times W'\) โดย \[\begin{eqnarray} H' &=& \left\lceil \frac{H - H_F}{S_H} \right\rceil + 1 \label{eq: deep conv pooling H} \\ W' &=& \left\lceil \frac{W - W_F}{S_W} \right\rceil + 1 \label{eq: deep conv pooling W} . \end{eqnarray}\]
ดังนั้น หากทำการดึงรวมด้วยฟิลเตอร์ขนาด \(2 \times 2\) ก้าวย่างขนาด \(2 \times 2\) ซึ่งเป็นการดึงรวมที่มักนิยมใช้ และอินพุตมีขนาด \(H \times W\) จะได้ แผนที่เอาต์พุตที่มีขนาด \(\left\lceil \frac{H}{2} \right\rceil \times \left\lceil \frac{W}{2} \right\rceil\) หรือ \(\frac{H}{2} \times \frac{W}{2}\) หาก \(H\) และ \(W\) เป็นเลขคู่ (หรือหาก \(H\) และ \(W\) เป็นเลขคี่ ขนาดของเอาต์พุตก็จะเป็น \((1 + \frac{H}{2}) \times (1 + \frac{W}{2})\) ซึ่งโดยมาก \(H >> 1, W >> 1\), ขนาดก็จะ \(\approx \frac{H}{2} \times \frac{W}{2}\)). นั่นคือ ขนาดแผนที่เอาต์พุตจะลดลงเหลือครึ่งหนึ่งของขนาดแผนที่อินพุต
ฟังก์ชันดึงรวม นิยมใช้ ฟังก์ชันทางสถิติ อาทิ ฟังก์ชันดึงรวมแบบมากที่สุด และ ฟังก์ชันดึงรวมแบบเฉลี่ย (average pooling) เป็นต้น. การทำงานของฟังก์ชันเหล่านี้ก็ตรงไปตรงมา คือ ฟังก์ชันดึงรวมแบบมากที่สุด จะให้ค่าที่มากที่สุดในเซตออกมา ฟังก์ชันดึงรวมแบบเฉลี่ย จะให้ค่าเฉลี่ยของค่าต่าง ๆ ในเซตออกมา.
6.3 เกรเดียนต์ของโครงข่ายคอนโวลูชั่น
ในขั้นตอนการฝึกโครงข่าย ขั้นตอนวิธีที่ใช้ มักอาศัยค่าเกรเดียนต์ (ดูหัวข้อ [sec: ANN training]). การใช้งานชั้นคอนโวลูชั่น และชั้นดึงรวม ก็มีผลต่อเกรเดียนต์. นอกจากนั้น ชั้นคอนโวลูชั่นเองก็มีค่าน้ำหนักที่ต้องการการฝึกด้วย.
6.3.1 เกรเดียนต์ของชั้นคอนโวลูชั่น
เปรียบเทียบกับหัวข้อ [sec: ANN backpropagation] พิจารณาความสัมพันธ์ ระหว่างฟังก์ชันเป้าหมายและชั้นคอนโวลูชั่น ฟังก์ชันเป้าหมาย \(E_n\) จะขึ้นกับค่าน้ำหนัก \(w_{fcij}\) (สมการ \(\eqref{eq: deep conv conv FxCxHxW}\) และ [deep conv 2Dconv Output]) ผ่านคอนโวลูชั่นเอาต์พุต \(a_{fkl}\) สำหรับทุก ๆ \(k\) และ \(l\) ที่ใช้ \(w_{fcij}\) ร่วม. ดังนั้นจากกฎลูกโซ่ \[\begin{eqnarray} \frac{\partial E_n}{\partial w_{fcij}} = \sum_{k=1}^{H'} \sum_{l=1}^{W'} \frac{\partial E_n}{\partial a_{fkl}} \frac{\partial a_{fkl}}{\partial w_{fcij}} \label{eq: deep conv grad E/w} \end{eqnarray}\]
เมื่อแทนค่าสมการ \(\eqref{eq: deep conv conv FxCxHxW}\) เข้าไปในสมการ \(\eqref{eq: deep conv grad E/w}\) จะได้ \[\begin{eqnarray} \frac{\partial E_n}{\partial w_{fcij}} = \sum_{k=1}^{H'} \sum_{l=1}^{W'} \frac{\partial E_n}{\partial a_{fkl}} \hat{x}_{c, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j} \label{eq: deep conv grad E/w 1} \end{eqnarray}\] โดย \(\hat{x}_{c, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j}\) เป็นอินพุตของชั้นคำนวณ (layer).
เมื่อกำหนด \[\begin{eqnarray} \delta_{fkl} \equiv \frac{\partial E_n}{\partial a_{fkl}} \label{eq: deep conv grad delta} \end{eqnarray}\] จะได้ \[\begin{eqnarray} \frac{\partial E_n}{\partial w_{fcij}} = \sum_{k=1}^{H'} \sum_{l=1}^{W'} \delta_{fkl} \hat{x}_{c, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j} \label{eq: deep conv grad E/w 2} \end{eqnarray}\] สำหรับ ดัชนี \(f = 1, \ldots, F\), ดัชนี \(c = 1, \ldots, C\), ดัชนี \(i = 1, \ldots, H_F\) และดัชนี \(j = 1, \ldots, W_F\) เมื่อ \(\hat{x}_{c, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j}\) คือ อินพุตของชั้นคอนโวลูชั่น ที่ผ่านการเติมเต็ม, \(S_H\) และ \(S_W\) เป็นค่าก้าวย่างตามแนวตั้งและนอน.
เมื่อเปรียบเทียบกับสมการ \(\eqref{eq: ANN BP dE/dw}\) จะเห็นว่าคล้ายกันมาก ต่างกันเพียง (1) สมการ \(\eqref{eq: deep conv grad E/w 2}\) มีการบวกพจน์ต่าง ๆ ที่ใช้ค่าน้ำหนักร่วมกัน (2) ค่าน้ำหนักไม่ได้เฉพาะเจาะจงกับเอาต์พุต (เพราะใช้ค่าน้ำหนักร่วมกัน), (3) จำนวนค่าน้ำหนักมีน้อยเมื่อเทียบกับจำนวนอินพุตและเอาต์พุต (ปกติ \(H_F << H\) และ \(W_F << W\)).
ในทำนองเดียวกัน เกรเดียนต์ของไบอัส สามารถหาได้จาก \[\begin{eqnarray} \frac{\partial E_n}{\partial b_f} = \sum_{k=1}^{H'} \sum_{l=1}^{W'} \delta_{fkl} \label{eq: deep conv grad E/b} . \end{eqnarray}\]
พิจารณา \(\delta_{fkl}\) ของชั้นที่ \(m^{th}\) ว่า \(a_{fkl}^{(m)}\) เชื่อมไปสู่เอาต์พุตสุดท้ายและฟังก์ชันจุดประสงค์ \(E_n\) ผ่านเอาต์พุตของชั้น \(z_{fkl}^{(m)}\) และจากกฎลูกโซ่ จะได้ \[\begin{eqnarray} \delta_{fkl}^{(m)} = \frac{\partial E_n}{\partial a_{fkl}^{(m)}} &=& \frac{\partial E_n}{\partial z_{fkl}^{(m)}} \cdot \frac{\partial z_{fkl}^{(m)}}{\partial a_{fkl}^{(m)}} \nonumber \end{eqnarray}\] โดยตัวยก \(\cdot^{(m)}\) เน้นระบุชั้นคำนวณ.
จากสมการ \(\eqref{eq: deep conv 2Dconv Output}\) จะได้ \[\begin{eqnarray} \delta_{fkl}^{(m)} &=& \frac{\partial E_n}{\partial z_{fkl}^{(m)}} \cdot h'\left(a_{fkl}^{(m)}\right) \label{eq: deep conv grad delta 1} \end{eqnarray}\]
โครงข่ายคอนโวลูชั่นจะมีชั้นคำนวณ \(3\) ชนิด ได้แก่ ชั้นคอนโวลูชั่น, ชั้นดึงรวม, และชั้นเชื่อมต่อเต็มที่ โดย การใช้งาน บางครั้งอาจมีหรือไม่มีชั้นดึงรวมหรือชั้นเชื่อมต่อเต็มที่ก็ได้ นอกจากนั้น จำนวนชั้นทั้งหมดและการเรียงลำดับของชั้นชนิดต่าง ๆ ก็อาจแตกต่างกันไป. การคำนวณค่า \(\frac{\partial E_n}{\partial z_{fkl}^{(m)}}\) ของชั้น \(m^{th}\) จะขึ้นกับชั้นคำนวณถัดไป (หรือฟังก์ชันจุดประสงค์ หากชั้น \(m^{th}\) เป็นชั้นสุดท้าย). เพื่อความสะดวก กำหนด \[\begin{eqnarray} \hat{\delta}_{fkl}^{(m)} \equiv \frac{\partial E_n}{\partial z_{fkl}^{(m)}} \label{eq: deep conv grad delta hat} . \end{eqnarray}\]
ดังนั้น เช่นเดียวกับโครงข่ายประสาทเทียมแบบเชื่อมต่อเต็มที่ การคำนวณการแพร่กระจายย้อนกลับของโครงข่ายคอนโวลูชั่น แต่ละชั้นจะคำนวณค่า \(\hat{\delta}\) ออกมาด้วย เพียงแต่ ค่า \(\hat{\delta}_{fkl}^{(m)}\) จะคำนวณมาจากชั้นที่ \((m+1)^{st}\) และชั้นที่ \(m^{th}\) ก็จะต้องคำนวณค่า \(\hat{\delta}_{fkl}^{(m-1)}\) เพื่อให้ชั้น \((m-1)^{st}\) สามารถนำไปคำนวณหาค่าเกรเดียนต์ของค่าน้ำหนักได้.
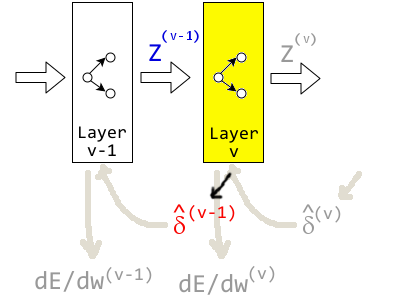
เนื่องจาก \(\hat{\delta}_{fkl}^{(m)}\) จะได้จากการคำนวณจากชั้นที่ \((m+1)^{st}\) จึงสะดวกกว่าที่ เมื่อพิจารณาชั้นคำนวณ \(v^{th}\) เราจะอภิปรายถึงการคำนวณหาค่า \(\hat{\delta}^{(v-1)}\) ซึ่งเน้นว่า ค่า \(\hat{\delta}^{(v-1)}\) นี้คำนวณจากชั้น \(v^{th}\) แต่นำไปใช้ในการหาค่าอนุพันธ์สำหรับชั้น \((v-1)^{st}\). รูป 1.19 แสดงภาพการผ่านค่า \(\hat{\delta}\) ที่คำนวณจากชั้น \(v^{th}\) เพื่อนำไปใช้คำนวณค่าเกรเดียนต์ของชั้น \((v-1)^{st}\).

เมื่อพิจารณาโครงข่ายคอนโวลูชั่น ชนิดของชั้นคำนวณก่อนหน้าของชั้นคอนโวลูชั่นจะเป็น ชั้นคำนวณคอนโวลูชั่น ชั้นดึงรวม หรืออินพุตได้เท่านั้น. โครงข่ายคอนโวลูชั่นไม่มีกรณีที่ชั้นเชื่อมต่อเต็มที่อยู่ก่อนหน้าชั้นคอนโวลูชั่น เพราะชั้นเชื่อมต่อเต็มที่ไม่มีโครงสร้างเชิงมิติของข้อมูล ดังนั้นหากจัดเรียงชั้นเชื่อมต่อเต็มก่อนชั้นคอนโวลูชั่น จึงไม่สามารถใช้ประโยชน์จากการคอนโวลูชั่นกับโครงสร้างเชิงมิติของข้อมูลได้.
ชนิดของชั้นคำนวณหลังจากชั้นคอนโวลูชั่น อาจเป็น ชั้นคอนโวลูชั่น ชั้นดึงรวม ชั้นเชื่อมต่อเต็มที่ หรือเอาต์พุตก็ได้.
6.3.1.0.1 กรณีชั้นเอาต์พุต
สำหรับกรณีชั้นคำนวณ \((v-1)^{st}\) เป็นชั้นคำนวณสุดท้าย และชั้นคำนวณ \((v-1)^{st}\) ต้องการค่า \(\hat{\delta}^{(v-1)} = \frac{\partial E_n}{\partial z^{(v-1)}}\) จากชั้นเอาต์พุต. รูป 1.20 แสดงการผ่านค่า \(\hat{\delta}\) จากชั้นเอาต์พุตกลับไปให้ชั้นคำนวณสุดท้าย.

ที่ชั้นเอาต์พุต4 ค่า \(\hat{\delta}^{(v-1)}\) ก็สามารถหาเกรเดียนต์ได้โดยตรง จากการแทนค่าฟังก์ชันจุดประสงค์ในพจน์ของตัวแปร \(z^{(v-1)}\) และการหาค่าอนุพันธ์.
ตัวอย่างเช่น ฟังก์ชันจุดประสงค์ \(E_n = \lambda \sum_{q=1}^F \sum_{r=1}^{H'} \sum_{s=1}^{W'} \left( y_{qrs} - z_{qrs}^{(v-1)} \right)^2\) เมื่อ \(\lambda\) เป็นค่าคงที่, \(F\) เป็นจำนวนชุดของเอาต์พุต, \(H'\) และ \(W'\) เป็นขนาดของเอาต์พุต, \(y_{qrs}\) เป็นเฉลย (ground-truth), และ \(z_{qrs}^{(v-1)}\) คือเอาต์พุตจากชั้น \((v-1)^{st}\).
ดังนั้น จากการแทนค่าฟังก์ชันจุดประสงค์ในพจน์ของเอาต์พุต \[\begin{eqnarray} \hat{\delta}_{fkl}^{(v-1)} &=& \frac{\partial \lambda \sum_{q=1}^F \sum_{r=1}^{H'} \sum_{s=1}^{W'} \left( y_{qrs} - z_{qrs}^{(v-1)} \right)^2}{\partial z_{fkl}^{(v-1)}} \nonumber \\ &=& -2 \lambda (y_{fkl} - z_{fkl}^{(v-1)}) \nonumber . \end{eqnarray}\] ดูหัวข้อ [sec: deep YOLO] เพิ่มเติมสำหรับตัวอย่างการใช้โครงข่ายคอนโวลูชั่น โดยใช้ชั้นคอนโวลูชั่นเป็นชั้นคำนวณสุดท้าย.
แต่หากชั้นคอนโวลูชั่นไม่ได้เป็นชั้นคำนวณสุดท้าย ค่า \(\hat{\delta}^{(v-1)}\) จะได้จากการคำนวณจากชั้นที่ \(v^{th}\) ตามชนิดของชั้น \(v^{th}\). รูป 1.21 แสดงแผนภาพการผ่านค่า \(\hat{\delta}^{(v-1)}\) กลับไปให้ชั้นก่อนหน้า.
6.3.1.0.2 กรณีชั้นเชื่อมต่อเต็มที่
พิจารณาชั้นที่ \(v^{th}\) เป็นชั้นเชื่อมต่อเต็มที่ ค่า \(\hat{\delta}_{fkl}^{(v-1)}\) คำนวณได้จาก เอาต์พุต \(z_{fkl}^{(v-1)}\) ของชั้น \((v-1)^{st}\) เชื่อมต่อไปถึงฟังก์ชันจุดประสงค์ \(E_n\) ผ่านชั้น \(v^{th}\) โดย เอาต์พุตของชั้น \((v-1)^{st}\) จะกลายเป็นอินพุตของชั้น \(v^{th}\).
เอาต์พุต \(z_{fkl}^{(v-1)}\) จากชั้นคอนโวลูชั่น เมื่อเข้าเป็นอินพุตของชั้นเชื่อมต่อเต็มที่ จะถูกสลายโครงสร้างลงเป็น \(z_q^{(v-1)}\) โดย \(z_{fkl} = z_q\) เมื่อ \(q = l + W' \cdot (k - 1) + H' W' \cdot (f - 1)\) สำหรับ \(f = 1, \ldots, F; k = 1, \ldots, H'; l = 1, \ldots, W'\).
ดังนั้น \[\begin{eqnarray} \hat{\delta}_{fkl}^{(v-1)} = \frac{\partial E_n}{\partial z_{fkl}^{(v-1)}} = \frac{\partial E_n}{\partial z_q^{(v-1)}} \label{eq: deep conv grad delta hat FC next 1} . \end{eqnarray}\]
ค่า \(\frac{\partial E_n}{\partial z_q^{(v-1)}}\) ก็สามารถหาได้ เช่นเดียวกับชั้นเชื่อมต่อเต็มที่ ซึ่งได้อภิปรายในหัวข้อ [sec: ann training].
6.3.1.0.3 ทบทวนเรื่องเกรเดียนต์ของชั้นเชื่อมต่อเต็มที่ (จากหัวข้อ [sec: ann training])
พิจารณาที่ชั้น \(v^{th}\) ซึ่งเป็นชั้นเชื่อมต่อเต็มที่. เอาต์พุตของชั้น \((v-1)^{st}\) ส่งอิทธิพลกับฟังก์ชันจุดประสงค์ \(E_n\) ผ่านชั้น \(v^{th}\) และ เมื่อใช้กฎลูกโซ่จะได้ \[\begin{eqnarray} \frac{\partial E_n}{\partial z_q^{(v-1)}} &=& \sum_{r=1}^R \frac{\partial E_n}{\partial a_r^{(v)}} \cdot \frac{\partial a_r^{(v)}}{\partial z_q^{(v-1)}} \nonumber \end{eqnarray}\] สำหรับ \(q = 1, \ldots, F \cdot H' \cdot W'\) เมื่อ \(a_r^{(v)}\) คือค่าการกระตุ้นของชั้นเชื่อมต่อเต็มที่ และ \(R\) คือจำนวนหน่วยซ่อนในชั้น \(v^{th}\). จาก \(a_r^{(v)} = \sum_q w_{rq}^{(v)} z_q^{(v-1)}\) และ \(\delta_r^{(v)} \equiv \frac{\partial E_n}{\partial a_r^{(v)}}\) ทำให้ได้ \[\begin{eqnarray} \frac{\partial E_n}{\partial z_q^{(v-1)}} &=& \sum_{r=1}^R \delta_r^{(v)} \cdot w_{rq}^{(v)} \nonumber \end{eqnarray}\] และค่า \(\delta_r^{(v)}\) ก็สามารถหาได้การแพร่กระจายย้อยกลับ ดังอภิปรายในหัวข้อ [sec: ann training] (สมการ \(\eqref{eq: backprop delta L}\) สำหรับชั้นคำนวณสุดท้าย หรือสมการ \(\eqref{eq: backprop delta q < L}\) สำหรับชั้นเชื่อมต่อเต็มที่ที่ไม่ใช่ชั้นคำนวณสุดท้าย)
6.3.1.0.4 กรณีชั้นคอนโวลูชั่น
ที่ชั้นคอนโวลูชั่น \(v^{th}\) ค่า \(\hat{\delta}_{fkl}^{(v-1)}\) ก็สามารถหาได้ในลักษณะเดียวกับชั้นเชื่อมต่อเต็มที่ เพียงแต่หน่วยเอาต์พุตของชั้นคอนโวลูชั่นที่ \((v-1)^{st}\) เชื่อมต่อกับหน่วยในชั้น \(v^{th}\) เฉพาะหน่วยที่สัมพันธ์กัน และค่าน้ำหนักมีการใช้ร่วมกัน.
หน่วย \(z_{fkl}^{(v-1)}\) ส่งอิทธิพลไปถึงฟังก์ชันจุดประสงค์ \(E_n\) ผ่านหน่วย \(a_{qrs}^{(v)}\) แต่หน่วย \(a_{qrs}^{(v)}\) เชื่อมต่อกับหน่วย \(z_{fkl}^{(v-1)}\) เฉพาะหน่วยที่สัมพันธ์กัน. รูป 1.22 แสดงการเชื่อมต่อของเอาต์พุตของชั้น \((v-1)^{st}\) กับเอาต์พุตของชั้น \(v^{th}\). ในรูปแสดงแผนภาพของชั้นคอนโวลูชั่นหนึ่งมิติ แต่การเชื่อมต่อชั้นคอนโวลูชั่นสองมิติ ก็ทำในลักษณะเดียวกัน.
เมื่อพิจารณาการเชื่อมต่อ จะพบว่า ตำแหน่งเอาต์พุตของชั้น \(v^{th}\) สัมพันธ์กับตำแหน่งเอาต์พุตของชั้น \((v-1)^{st}\) โดย สำหรับแต่ละลักษณะสำคัญ \(q\), หน่วย \(a_{qrs}^{(v)}\) เชื่อมต่อ \(z_{fkl}^{(v-1)}, f = 1, \ldots, F\) เมื่อ \(F\) คือจำนวนลักษณะสำคัญของชั้น \((v-1)^{st}\), \(r \in \Omega(k, S_H, H_F)\), \(s \in \Omega(l, S_W, W_F)\), ขนาดก้าวย่างกับขนาดฟิลเตอร์ของชั้น \(v^{th}\) คือ \(S_H \times S_W\) กับ \(H_F \times W_F\) ตามลำดับ, และ ฟังก์ชันเซต \[\begin{eqnarray} \Omega(k, S, H_F) & = & \left\{ \frac{k - i}{S} + 1: (k - i \geq 0) \;\mathrm{and}\; \left( (k - i) \;\mathrm{mod}\; S = 0 \right) \right\}_{i = 1, \ldots, H_F} \label{eq: deep conv back r set} \end{eqnarray}\]
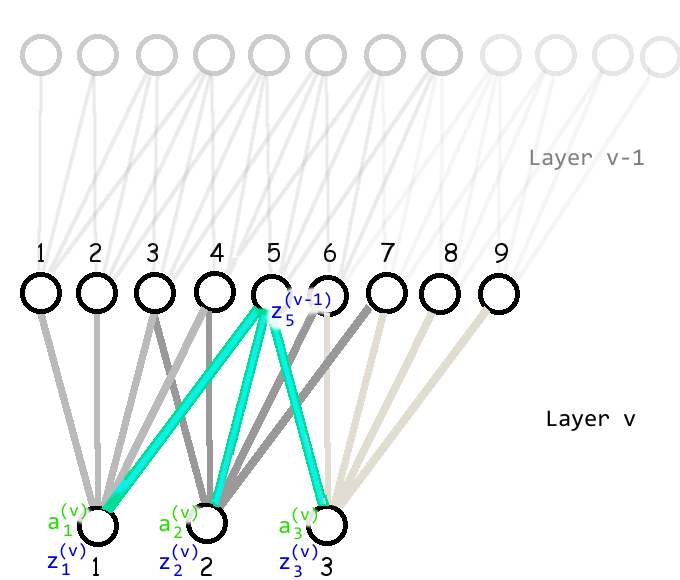
ตัวอย่างเช่น หน่วยเอาต์พุต \(z_{fkl}^{(v-1)}\) สำหรับ \(f=1,\ldots,4; k=1,\ldots,5; l=1,\ldots,5\). นั่นคือ ชั้น \((v-1)^{st}\) มีสี่ลักษณะสำคัญ ที่เกิดจากการใช้ฟิลเตอร์สี่ตัว และได้แผนที่ลักษณะสำคัญแต่ละอันเป็นขนาด \(5 \times 5\). เมื่อ หน่วยเอาต์พุตในชั้น \((v-1)^{st}\) เชื่อมต่อกับชั้น \(v^{th}\) ที่เป็นชั้นคอนโวลูชั่น โดยชั้น \(v^{th}\) มีแปดลักษณะสำคัญ (\(q = 1, \ldots, 8\)) ใช้ฟิลเตอร์ขนาด \(3 \times 3\) สำหรับแต่ละลักษณะสำคัญ และใช้ขนาดก้าวย่างเป็น \(1 \times 1\) แล้วดังนั้น หน่วย(คอนโวลูชั่นเอาต์พุต)ของชั้น \((v-1)^{st}\) เชื่อมต่อกับหน่วย(คอนโวลูชั่นเอาต์พุต)ของชั้น \(v^{th}\) ดังนี้
\(\bullet\) \(z_{1,1,1}^{(v-1)}\) เชื่อมต่อกับ \(a_{1,1,1}^{(v)}, \ldots, a_{8,1,1}^{(v)}\)
จาก \(z_{1,1,1}^{(v-1)}\) เชื่อมต่อกับ \(a_{qrs}^{(v)}\) สำหรับ ทุก ๆ \(q = 1,\ldots, 8; r = 1; s = 1\) เพราะว่า \(z_{1,1,1}^{(v-1)}\) มี \(f = 1, k = 1, l = 1\). ที่ \(k = 1\) ทำให้ \(r \in \Omega(k=1, S=1, H=3)\). เมื่อแทนค่าลงในสมการ \(\eqref{eq: deep conv back r set}\) จะได้ว่า \(r \in \{\frac{1 - i}{1} + 1: (1 - i \geq 0) \;\mathrm{and}\; ( (1 - i) \;\mathrm{mod}\; 1 = 0) \}_{i = 1, \ldots, 3}\) และเมื่อพิจารณาสมาชิกกับเงื่อนไข. ที่ \(i = 1\), สมาชิก \(\frac{1 - 1}{1} + 1 = 1\). ที่ \(i = 2\), ค่า \(1 - 2 < 0\) ไม่ผ่านเงื่อนไขแรก. ที่ \(i = 3\), ค่า \(1 - 3 < 0\) ไม่ผ่านเงื่อนไขแรก. ดังนั้นที่ \(k = 1\) ทำให้ \(r \in \{1\}\) และในทำนองเดียวกัน ที่ \(l = 1\) ทำให้ \(s \in \{1\}\).
\(\bullet\) \(z_{1,2,1}^{(v-1)}\) เชื่อมต่อกับ \(a_{1,1,1}^{(v)}, \ldots, a_{8,1,1}^{(v)}, a_{1,2,1}^{(v)}, \ldots, a_{8,2,1}^{(v)},\)
จาก \(z_{1,1,1}^{(v-1)}\) เชื่อมต่อกับ \(a_{qrs}^{(v)}\) สำหรับ ทุก ๆ \(q = 1,\ldots, 8; r = 1, 2; s = 1\) เพราะว่า \(k = 2\) ทำให้ \(r \in \{1, 2\}\) จาก \(r \in \{\frac{2 - i}{1} + 1: (2 - i \geq 0) \;\mathrm{and}\; ( (2 - i) \;\mathrm{mod}\; 1 = 0) \}_{i = 1, \ldots, 3}\). ที่ \(i = 1\), สมาชิก \(\frac{2 - 1}{1} + 1 = 2\). ที่ \(i = 2\), สมาชิก \(\frac{2 - 2}{1} + 1 = 1\). ที่ \(i = 3\), ค่า \(2 - 3 < 0\) ไม่ผ่านเงื่อนไขแรก.
\(\bullet\) \(z_{1,3,1}^{(v-1)}\) เชื่อมต่อกับ \(a_{1,1,1}^{(v)}, \ldots, a_{8,1,1}^{(v)},\) \(a_{1,2,1}^{(v)}, \ldots, a_{8,2,1}^{(v)},\) \(a_{1,3,1}^{(v)}, \ldots, a_{8,3,1}^{(v)},\)
\(k = 3\) ทำให้ \(r \in \{1, 2, 3\}\)
\(\bullet\) \(z_{1,4,1}^{(v-1)}\) เชื่อมต่อกับ \(a_{1,2,1}^{(v)}, \ldots, a_{8,2,1}^{(v)},\) \(a_{1,3,1}^{(v)}, \ldots, a_{8,3,1}^{(v)},\) \(a_{1,4,1}^{(v)}, \ldots, a_{8,4,1}^{(v)},\)
\(k = 4\) ทำให้ \(r \in \{2, 3, 4\}\)
\(\vdots\)
\(\bullet\) \(z_{1,5,5}^{(v-1)}\) เชื่อมต่อกับ
\(a_{1,3,3}^{(v)}, \ldots, a_{8,3,3}^{(v)},\) \(a_{1,4,3}^{(v)}, \ldots, a_{8,4,3}^{(v)},\) \(a_{1,5,3}^{(v)}, \ldots, a_{8,5,3}^{(v)},\)
\(a_{1,3,4}^{(v)}, \ldots, a_{8,3,4}^{(v)},\) \(a_{1,4,4}^{(v)}, \ldots, a_{8,4,4}^{(v)},\) \(a_{1,5,4}^{(v)}, \ldots, a_{8,5,4}^{(v)},\)
\(a_{1,3,5}^{(v)}, \ldots, a_{8,3,5}^{(v)},\) \(a_{1,4,5}^{(v)}, \ldots, a_{8,4,5}^{(v)},\) \(a_{1,5,5}^{(v)}, \ldots, a_{8,5,5}^{(v)},\)
\(k = 5\) ทำให้ \(r \in \{3, 4, 5\}\). \(l = 5\) ทำให้ \(s \in \{3, 4, 5\}\).
\(\vdots\)
\(\bullet\) \(z_{4,5,5}^{(v-1)}\) เชื่อมต่อกับ
\(a_{1,3,3}^{(v)}, \ldots, a_{8,3,3}^{(v)},\) \(a_{1,4,3}^{(v)}, \ldots, a_{8,4,3}^{(v)},\) \(a_{1,5,3}^{(v)}, \ldots, a_{8,5,3}^{(v)},\)
\(a_{1,3,4}^{(v)}, \ldots, a_{8,3,4}^{(v)},\) \(a_{1,4,4}^{(v)}, \ldots, a_{8,4,4}^{(v)},\) \(a_{1,5,4}^{(v)}, \ldots, a_{8,5,4}^{(v)},\)
\(a_{1,3,5}^{(v)}, \ldots, a_{8,3,5}^{(v)},\) \(a_{1,4,5}^{(v)}, \ldots, a_{8,4,5}^{(v)},\) \(a_{1,5,5}^{(v)}, \ldots, a_{8,5,5}^{(v)},\)
\(k = 5\) ทำให้ \(r \in \{2, 3, 4\}\) และ \(l = 5\) ทำให้ \(s \in \{2, 3, 4\}\)
เป็นต้น.
สังเกต (1) ดัชนีเชิงลำดับ \(k\) และ \(l\) ของชั้น \((v-1)^{st}\) จะบอกดัชนีเชิงลำดับ \(r\) และ \(s\) สำหรับทุก ๆ ดัชนีอิสระ \(q\) ของหน่วยในชั้น \(v^{th}\) . ตาราง 1.1 แสดงความสัมพันธ์ตำแหน่งหน่วยที่ \(k\) ในชั้น \((v-1)^{st}\) กับตำแหน่งหน่วยที่ \(r\) ในชั้น \(v^{th}\). ดัชนี \(l\) ก็เป็นในลักษณะเดียวกัน. (2) หน่วยที่มีตำแหน่งเชิงลำดับเดียวกัน แต่ต่างตำแหน่งอิสระ เช่น \(z_{1, 5, 5}\) กับ \(z_{4, 5, 5}\) เชื่อมต่อกับหน่วยเดียวกัน.
| ก้าวย่าง | \(S_H = 1\) | \(S_H = 2\) | ||
|---|---|---|---|---|
| ฟิลเตอร์ | \(H_F = 3\) | \(H_F = 5\) | \(H_F = 3\) | \(H_F = 5\) |
| \(k=1\) | \(r \in \{1\}\) | \(r \in \{1\}\) | \(r \in \{1\}\) | \(r \in \{1\}\) |
(1, x, x) |
(1, x, x, x, x) |
(1, x, x) |
(1, x, x, x, x) |
|
| \(k=2\) | \(r \in \{1, 2\}\) | \(r \in \{1, 2\}\) | \(r \in \{1\}\) | \(r \in \{1\}\) |
(2, 1, x) |
(2 ,1, x, x, x) |
(-, 1, x) |
(-, 1, x, x, x) |
|
| \(k=3\) | \(r \in \{1, 2, 3\}\) | \(r \in \{1, 2, 3\}\) | \(r \in \{1, 2\}\) | \(r \in \{1, 2\}\) |
(3, 2, 1) |
(3, 2, 1, x, x) |
(2, -, 1) |
(2, -, 1, x, x) |
|
| \(k=4\) | \(r \in \{2, 3, 4\}\) | \(r \in \{1, 2, 3, 4\}\) | \(r \in \{2\}\) | \(r \in \{1, 2\}\) |
(4, 3, 2) |
(4, 3, 2, 1, x) |
(-, 2, -) |
(-, 2, -, 1, x) |
|
| \(k=5\) | \(r \in \{3, 4, 5\}\) | \(r \in \{1, 2, 3, 4, 5\}\) | \(r \in \{2, 3\}\) | \(r \in \{1, 2, 3\}\) |
(5, 4, 3) |
(5, 4, 3, 2, 1) |
(3, -, 2) |
(3, -, 2, -, 1) |
|
[tbl: deep conv grad back]
จากการเชื่อมต่อข้างต้น เมื่อพิจารณาชั้นคอนโวลูชั่นที่ \(v^{th}\), หน่วย \(z_{fkl}^{(v-1)}\) เชื่อมต่อไปสู่เอาต์พุตสุดท้ายและค่าฟังก์ชันจุดประสงค์ ผ่าน \(a_{qrs}^{(v)}\) และจากกฎลูกโซ่ จะได้ \[\begin{eqnarray} \hat{\delta}_{fkl}^{(v-1)} = \frac{\partial E_n}{\partial z_{fkl}^{(v-1)}} = \sum_{q=1}^Q \sum_{r \in \Omega_r} \sum_{s \in \Omega_s} \frac{\partial E_n}{\partial a_{qrs}^{(v)}} \frac{\partial a_{qrs}^{(v)}}{\partial z_{fkl}^{(v-1)}} \label{eq: deep conv delta layer m 1} \end{eqnarray}\] เมื่อ \(Q\) คือจำนวนลักษณะสำคัญในชั้น \(v^{th}\), \(\Omega_r = \Omega(k, S_H, H_F)\) และ \(\Omega_s = \Omega(l, S_W, W_F)\), โดย \(H_F \times W_F\) และ \(S_H \times S_W\) เป็นขนาดฟิลเตอร์และขนาดก้าวย่างในชั้น \(v^{th}\) ตามลำดับ.
จากนิยาม \(\eqref{eq: deep conv grad delta}\) และการคำนวณคอนโวลูชั่นสมการ \(\eqref{eq: deep conv conv FxCxHxW}\) (อินพุต \(\boldsymbol{\hat{X}}\) ในสมการ \(\eqref{eq: deep conv conv FxCxHxW}\) คือ อินพุตของชั้น \(v^{th}\) ซึ่งก็คือเอาต์พุตของชั้นก่อนหน้า, นั่นคือ \(\boldsymbol{\hat{X}} \equiv \boldsymbol{Z}^{(v-1)}\) และ เพื่อให้ตัวแปรดัชนีฟิลเตอร์จำแนกได้ง่าย ที่นี้ใช้ดัชนี \(\hat{f}\) แทนดัชนีฟิลเตอร์ สำหรับการคำนวณคอนโวลูชั่น), เมื่อแทนค่าลงไปในสมการ \(\eqref{eq: deep conv delta layer m 1}\) จะได้ว่า \[\begin{eqnarray} \frac{\partial E_n}{\partial z_{fkl}^{(v-1)}} &=& \sum_q \sum_r \sum_s \delta_{qrs}^{(v)} \frac{\partial \left(b_{q,r,s}^{(v)} + \sum_{\hat{f}} \sum_i \sum_j w_{q\hat{f}ij}^{(v)} z_{\hat{f}, S_H \cdot (r - 1) + i, S_W \cdot (s - 1) + j}^{(v-1)} \right)}{\partial z_{fkl}^{(v-1)}} \nonumber \\ &=& \sum_q \sum_r \sum_s \delta_{qrs}^{(v)} \cdot w_{q,f,k-S_H \cdot (r - 1),l-S_W \cdot (s - 1)}^{(v)} \label{eq: deep conv delta layer m 3} . \end{eqnarray}\]
สังเกตว่า เพื่อคำนวณหา \(\hat{\delta}_{fkl}^{(v-1)} \equiv \frac{\partial E_n}{\partial z_{fkl}^{(v-1)}}\) สำหรับส่งไปให้ชั้น \((v-1)^{st}\), ชั้น \(v^{th}\) ต้องคำนวณ \(\delta_{qrs}^{(v)}\) และ จากสมการ \(\eqref{eq: deep conv grad delta 1}\) ค่า \(\delta_{qrs}^{(v)} = \frac{\partial E_n}{\partial z_{qrs}^{(v)}} \cdot h'\left(a_{qrs}^{(v)}\right)\) เมื่อ \(h'(\cdot)\) คืออนุพันธ์ของฟังก์ชันกระตุ้นชั้น \(v^{th}\). ส่วนค่า \(\frac{\partial E_n}{\partial z_{qrs}^{(v)}} \equiv \hat{\delta}_{qrs}^{(v)}\) ก็ได้มาจากชั้น \((v+1)^{st}\) อีกทอดหนึ่ง. หัวข้อ 1.4 และรายการ [lst: deep code convnet numpy] แสดงตัวอย่างโปรแกรมโครงข่ายคอนโวลูชั่น.
6.3.1.0.5 ขนาดก้าวย่างที่นิยม
พิจารณา \(\hat{\delta}_{fkl}^{(v-1)}\) สำหรับกรณีชั้น \(v^{th}\) ใช้ก้าวย่างขนาด \(1 \times 1\) ซึ่งเป็นขนาดที่มักถูกใช้กับชั้นคอนโวลูชั่น. กรณีนี้จะทำให้ \[\begin{eqnarray} \Omega_r &=& \{k - i + 1: k - i \geq 0 \}_{i = 1,\ldots,H_F} \label{eq: deep conv grad omega r 1x1} , \\ \Omega_s &=& \{l - i + 1: l - i \geq 0 \}_{i = 1,\ldots,W_F} \label{eq: deep conv grad omega s 1x1} . \end{eqnarray}\] และ \[\begin{eqnarray} \hat{\delta}_{fkl}^{(v-1)} &=& \sum_{q=1}^Q \sum_{r \in \Omega_r} \sum_{s \in \Omega_s} \delta_{qrs}^{(v)} \cdot w_{q,f, k - r + 1, l - s + 1} \label{eq: deep delta hat stride 1x1} \end{eqnarray}\] เมื่อแทนสมการ \(\eqref{eq: deep conv grad omega r 1x1}\) และ \(\eqref{eq: deep conv grad omega s 1x1}\) ลงในสมการข้างต้น และเขียน \(r\) และ \(s\) ในรูป \(i\) และ \(j\) จะได้ \[\begin{eqnarray} \hat{\delta}_{fkl}^{(v-1)} &=& \sum_{q=1}^Q \sum_{i \in \{1, \ldots, H_F: i \leq k\}} \sum_{j \in \{1, \ldots, W_F: j \leq l\}} \delta_{q, k - i + 1, l - j + 1}^{(v)} \cdot w_{q,f, i, j} \nonumber \end{eqnarray}\] หรือ \[\begin{eqnarray} \hat{\delta}_{fkl}^{(v-1)} &=& \sum_{q=1}^Q \sum_{i = 1}^{H_F} \sum_{j = 1}^{W_F} \delta_{q, k - i + 1, l - j + 1}^{(v)} \cdot w_{q,f, i, j} \label{eq: deep delta stride 1x1 clean} \end{eqnarray}\] สำหรับ \(k \geq i\) และ \(l \geq j\).
6.3.1.0.6 กรณีชั้นดึงรวม
หากชั้น \(v^{th}\) เป็นชั้นดึงรวม หน่วย \(z_{fkl}^{(v-1)}\) เชื่อมต่อไปสู่เอาต์พุตสุดท้ายและค่าฟังก์ชันจุดประสงค์ ผ่านหน่วย \(a_{frs}^{(v)}\). สังเกตว่า เนื่องจากชั้นดึงรวมไม่ได้ประมวลผลในชุดมิติของมิติอิสระ ดังนั้น หน่วยของชั้นดึงรวมในลักษณะสำคัญ \(f\) เกี่ยวข้องกับหน่วยก่อนหน้าในลักษณะสำคัญ \(f\) เช่นกันเท่านั้น. ชั้นดึงรวมรักษาชุดมิติอิสระไว้ (ขนาดชุดมิติอิสระของอินพุตและเอาต์พุตเท่ากัน).
พิจารณาการคำนวณเอาต์พุตของชั้นดึงรวม (สมการ \(\eqref{eq: deep conv pooling}\)) \[\begin{eqnarray} z_{frs}^{(v)} = g( \{ z_{f, S_H \cdot (r-1)+i, S_W \cdot (s-1)+j}^{(v-1)} \}_{i=1,\ldots, H_F, j=1,\ldots, W_F} ) \label{eq: deep pooling z = g(set)} \end{eqnarray}\] เมื่อ \(\{ z_{f, S_H \cdot (r-1)+i, S_W \cdot (s-1)+j}^{(v-1)} \}_{i=1,\ldots, H_F, j=1,\ldots, W_F}\) เป็นเซตของหน่วยต่าง ๆ ที่ถูกดึงมารวมกัน, \(g(\cdot)\) เป็นฟังก์ชันดึงรวม, และ \(z_{frs}^{(v)}\) คือเอาต์พุตของชั้น \(v^{th}\) ซึ่งเป็นชั้นดึงรวม โดย \(S_H \times S_W\) กับ \(H_F \times W_F\) คือขนาดก้าวย่างกับขนาดฟิลเตอร์ ของชั้น \(v^{th}\) ตามลำดับ.
สังเกตความสัมพันธ์ระหว่าง \(z_{fkl}^{(v-1)}\) กับ \(z_{frs}^{(v)}\) ในชั้นดึงรวม จะคล้ายกับความสัมพันธ์ในชั้นคอนโวลูชั่น โดยต่างกันที่ (1) ชั้นดึงรวมไม่มีการคำนวณค่ากระตุ้น \(a\) และ (2) ชั้นดึงรวมไม่ได้ประมวลผลในชุดมิติของมิติอิสระ. แต่หากมองเฉพาะความสัมพันธ์ในชุดมิติเชิงลำดับ จะพบว่าหน่วยในชั้นดึงรวมมีความสัมพันธ์กับหน่วยในชั้นติดกัน ในลักษณะเดียวกับชั้นคอนโวลูชั่น (เปรียบเทียบดัชนีชุดมิติเชิงลำดับ สมการ \(\eqref{eq: deep conv pooling}\) กับ สมการ \(\eqref{eq: deep conv conv FxCxHxW}\)) ดังนั้น เมื่อโยงความสัมพันธ์ย้อนกลับ ชั้นดึงรวมก็สามารถใช้ฟังก์ชัน \(\Omega(\cdot)\) ในสมการ \(\eqref{eq: deep conv back r set}\) ช่วยอธิบายความสัมพันธ์ได้ในลักษณะเดียวกัน.
เมื่อพิจารณา \(\hat{\delta}_{fkl}^{(v-1)} \equiv \frac{\partial E_n}{\partial z_{fkl}^{(v-1)}}\) และจากกฎลูกโซ่ จะได้ \[\begin{eqnarray} \frac{\partial E_n}{\partial z_{fkl}^{(v-1)}} = \sum_{r \in \Omega_r} \sum_{s \in \Omega_s} \frac{\partial E_n}{\partial z_{frs}^{(v)}} \frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}} \label{eq: deep conv delta layer m 1 next pooling} \end{eqnarray}\] เมื่อ \(\Omega_r = \Omega(k, S_H, H_F)\) และ \(\Omega_s = \Omega(l, S_W, W_F)\).
เมื่อแทน \(\frac{\partial E_n}{\partial z_{frs}^{(v)}} = \hat{\delta}_{frs}^{(v)}\) ลงไปจะได้ \[\begin{eqnarray} \frac{\partial E_n}{\partial z_{fkl}^{(v-1)}} = \sum_{r \in \Omega_r} \sum_{s \in \Omega_s} \hat{\delta}_{frs}^{(v)} \frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}} \label{eq: deep conv grad delta hat next pooling} . \end{eqnarray}\]
ชั้น \(v^{th}\) รับค่า \(\hat{\delta}_{frs}^{(v)}\) มาจากชั้น \((v+1)^{st}\). ส่วนค่า \(\frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}}\) สามารถคำนวณได้ในชั้น \(v^{th}\) นี้ โดยการหาอนุพันธ์ ดังนี้ \[\begin{eqnarray} \frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}} &=& \frac{\partial g( \{ z_{f, S_H \cdot (r-1)+i, S_W \cdot (s-1)+j}^{(v-1)} \}_{i=1,\ldots, H_F, j=1,\ldots, W_F} )}{\partial z_{fkl}^{(v-1)}} \end{eqnarray}\] ซึ่งผลการหาอนุพันธ์จะขึ้นกับฟังก์ชันดึงรวม. พิจารณาฟังก์ชันดึงรวม \(3\) แบบ ได้แก่ แบบมากที่สุด (max pooling), แบบเฉลี่ย (average pooling), และแบบอาร์เอ็มเอส (root-mean-squared pooling หรือ rms pooling).
6.3.1.0.7 เมื่อใช้การดึงรวมแบบมากที่สุด
นั่นคือ ฟังก์ชันดึงรวม \(g( \{ z_1, \ldots, z_n \} )\) \(=\) \(\max\{ z_1, \ldots, z_n \}\) และจะได้ว่า \[\begin{eqnarray} \frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}} &=& \left\{ \begin{array}{l l} 1 & \;\mbox{เมื่อ}\; z_{fkl}^{(v-1)} = \max\{ \{ z_{f, S_H \cdot (r-1)+i, S_W \cdot (s-1)+j}^{(v-1)} \}_{i=1,\ldots, H_F, j=1,\ldots, W_F} \}, \\ 0 & \;\mbox{เมื่อ}\; z_{fkl}^{(v-1)} \neq \max\{ \{ z_{f, S_H \cdot (r-1)+i, S_W \cdot (s-1)+j}^{(v-1)} \}_{i=1,\ldots, H_F, j=1,\ldots, W_F} \}. \end{array} \right. \nonumber \\ \; \label{eq: deep conv grad max pool} . \end{eqnarray}\]
6.3.1.0.8 เมื่อใช้การดึงรวมแบบเฉลี่ย
นั่นคือ ฟังก์ชันดึงรวม \(g( \{ z_1, \ldots, z_n \} ) = \frac{1}{n} \sum_{i=1}^n z_i\) และจะได้ว่า \[\begin{eqnarray} \frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}} &=& \frac{1}{H_F W_F} \label{eq: deep conv grad average pool} . \end{eqnarray}\]
6.3.1.0.9 เมื่อใช้การดึงรวมแบบอาร์เอ็มเอส
นั่นคือ ฟังก์ชันดึงรวม \(g( \{ z_1, \ldots, z_n \} ) = \sqrt{\frac{1}{n} \sum_{i=1}^n z_i^2}\) และจะได้ว่า \[\begin{eqnarray} \frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}} &=& \frac{z_{fkl}^{(v-1)}}{H_F W_F \cdot z_{frs}^{(v)}} \label{eq: deep conv grad rms pool} \end{eqnarray}\]
ชั้นดึงรวมเองไม่มีค่าน้ำหนักที่ต้องปรับ จึงไม่ต้องคำนวณเกรเดียนต์เทียบน้ำหนักของชั้น แต่ชั้นดึงรวมต้องผ่านค่า \(\hat{\delta}_{fkl}^{(v-1)} = \frac{\partial E_n}{\partial z_{fkl}^{(v-1)}}\) ไปให้ชั้น \((v-1)^{st}\).
6.4 สรุปการคำนวณของโครงข่ายคอนโวลูชั่นสองมิติ.
กำหนดให้อินพุตที่ผ่านการเติมเต็ม \(\boldsymbol{Z}^{(0)} \in \mathbb{R}^{C \times H' \times W'}\). คำนวณการแพร่กระจายไปข้างหน้า ตามชนิดของชั้นคำนวณ สำหรับชั้น \(m = 1, \ldots, M\) เมื่อ \(M\) คือจำนวนชั้นคำนวณทั้งหมด ดังนั้นเอาต์พุตของโครงข่าย คือเอาต์พุตของชั้นสุดท้าย. นั่นคือ \(\boldsymbol{Z}^{(M)}\) เป็นเอาต์พุตสุดท้าย.
6.4.0.0.1 กรณีชั้นคอนโวลูชั่น
คำนวณสมการ \(\eqref{eq: deep conv conv FxCxHxW}\) และ \(\eqref{eq: deep conv 2Dconv Output}\) นั่นคือ \[\begin{eqnarray} a_{f,k,l}^{(m)} &=& b_f^{(m)} + \sum_{c=1}^C \sum_{i=1}^{H_F} \sum_{j=1}^{W_F} w_{fcij}^{(m)} \cdot z_{c, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j}^{(m-1)} \nonumber \\ z_{f,k,l}^{(m)} &=& h^{(m)}(a_{f,k,l}^{(m)}) \nonumber \end{eqnarray}\] สำหรับ \(f = 1, \ldots, F\), \(k = 1, \ldots, H\) และ \(l = 1, \ldots, W\) เมื่อ \(b_f^{(m)}, w_{fcij}^{(m)}\) คือ ค่าไบอัส และค่าน้ำหนักของชั้น \(m^{th}\), \(h^{(m)}\) คือฟังก์ชันกระตุ้นของชั้น \(m^{th}\), โดย \(F, H, W\) คือจำนวนลักษณะสำคัญและขนาดของแผนที่เอาต์พุตของชั้น \(m^{th}\), \(H_F, W_F\) คือขนาดฟิลเตอร์ของชั้น \(m^{th}\) ตามแนวตั้งและนอนตามลำดับ และ \(S_H, S_W\) คือขนาดก้าวย่างของชั้น \(m^{th}\) ตามแนวตั้งและนอนตามลำดับ.
6.4.0.0.2 กรณีชั้นดึงรวม
คำนวณสมการ \(\eqref{eq: deep conv pooling}\). นั่นคือ \[\begin{eqnarray} z_{f,k,l}^{(m)} &=& g^{(m)}( \{ z_{f, S_H \cdot (k-1)+i, S_W \cdot (l-1)+j}^{(m-1)} \}_{i=1,\ldots, H_F, j=1,\ldots, W_F} ) \nonumber \end{eqnarray}\] สำหรับ \(f = 1, \ldots, F\), \(k = 1, \ldots, H\) และ \(l = 1, \ldots, W\) เมื่อ \(g^{(m)}\) คือฟังก์ชันดึงรวมของชั้น \(m^{th}\), โดย \(F, H, W\) คือจำนวนลักษณะสำคัญและขนาดของแผนที่เอาต์พุตของชั้น \(m^{th}\), \(H_F, W_F\) คือขนาดฟิลเตอร์ของชั้น \(m^{th}\) ตามแนวตั้งและนอนตามลำดับ และ \(S_H, S_W\) คือขนาดก้าวย่างของชั้น \(m^{th}\) ตามแนวตั้งและนอนตามลำดับ.
6.4.0.0.3 กรณีชั้นเชื่อมต่อเต็มที่
สลายโครงสร้างอินพุต (ถ้าจำเป็น). นั่นคือคำนวณ \[z_q^{(m-1)} = z_{fkl}^{(m-1)} \nonumber\] เมื่อ \(q = l + W' \cdot (k - 1) + H' W' \cdot (f - 1)\) สำหรับ \(f = 1, \ldots, F'; k = 1, \ldots, H'; l = 1, \ldots, W'\) โดย \(F', H', W'\) คือจำนวนลักษณะสำคัญ, ขนาดเอาต์พุตแนวตั้ง, ขนาดเอาต์พุตแนวนอนของชั้น \((m-1)^{st}\) ตามลำดับ.
คำนวณชั้นเชื่อมต่อเต็มที่ สมการ \(\eqref{eq: ANN neural activation}\) และ \(\eqref{eq: ANN neural output}\). นั่นคือ \[\begin{eqnarray} a_f^{(m)} &=& b_f^{(m)} + \sum_{q=1}^Q w_{fq}^{(m)} z_q^{(m-1)} \nonumber \\ z_f^{(m)} &=& h^{(m)}(a_f^{(m)}) \nonumber \end{eqnarray}\] สำหรับ \(f = 1, \ldots, F\) เมื่อ \(b_f^{(m)}\), \(w_{fq}^{(m)}\), \(h^{(m)}\) คือค่าไบอัส ค่าน้ำหนัก และฟังก์ชันกระตุ้นของชั้น \(m^{th}\) โดย \(F\) เป็นจำนวนหน่วยเอาต์พุตในชั้น \(m^{th}\).
6.4.1 เกรเดียนต์ของโครงข่ายคอนโวลูชั่น
เกรเดียนต์ของโครงข่ายคอนโวลูชั่นสามารถหาได้ โดยใช้การแพร่กระจายย้อนกลับ โดยคำนวณทีละชั้นคำนวณ เริ่มจากเอาต์พุต แล้วไปชั้นสุดท้าย แล้วไล่ย้อนกลับไปทีละชั้นจนครบทุกชั้น. นั่นคือ หากชั้นคำนวณมีจำนวน \(M\) ชั้น วิธีแพร่กระจายย้อนกลับจะเริ่มที่เอาต์พุต (นับเป็น ชั้น \((M+1)^{st}\)) แล้วไล่ย้อนกลับไปจนถึงชั้นแรก (ชั้น \(1^{st}\)).
ค่าที่แต่ละชั้น \(v^{th}\) ต้องส่งย้อนกลับไปให้ชั้นก่อนหน้า คือ ค่า \(\hat{\delta}_{fkl}^{(v-1)} \equiv \frac{\partial E_n}{\partial z_{fkl}^{(v-1)}}\) สำหรับ \(f = 1, \ldots, F'\); \(k = 1, \ldots, H'\); \(l = 1, \ldots, W'\) เมื่อ \(F', H', W'\) คือ จำนวนลักษณะสำคัญ ขนาดเอาต์พุตในแนวตั้ง ขนาดเอาต์พุตในแนวนอน ของชั้น \((v-1)^{st}\) ตามลำดับ.
6.4.1.0.1 กรณีเอาต์พุต
ในทีนี้ หมายถึง การคำนวณแรกสุด (ก่อนการคำนวณชั้นสุดท้าย). ที่กรณีชั้น \(v^{th}\) เป็นเอาต์พุต (\(v = M+1\)) เอาต์พุตไม่มีค่าน้ำหนักที่ต้องปรับ แต่ต้องการคำนวณ \(\hat{\delta}^{(v-1)} = \hat{\delta}^{(M)}\) เพื่อส่งกลับให้ชั้นคำนวณสุดท้าย.
ค่า \(\hat{\delta}_{fkl}^{(M)}\) สามารถหาได้จาก \[\hat{\delta}_{fkl}^{(M)} = \frac{\partial E_n}{\partial z_{fkl}^{(M)}} \nonumber\] ซึ่งมักหาได้ไม่ยาก เนื่องจากฟังก์ชันจุดประสงค์ \(E_n\) มักถูกนิยามในพจน์ของ \(z_{fkl}^{(M)}\).
6.4.1.0.2 กรณีชั้นเชื่อมต่อเต็มที่
ที่กรณีชั้น \(v^{th}\) เป็นชั้นเชื่อมต่อเต็มที่ ชั้น \(v^{th}\) รับ \(\hat{\delta}_j^{(v)}\) มาจากชั้น \((v+1)^{st}\) และชั้น \(v^{th}\) คำนวณเกรเดียนต์เทียบกับน้ำหนักของชั้นจากสมการ \(\eqref{eq: ANN BP dE/dw}\). นั่นคือ \[\begin{eqnarray} \frac{\partial E_n}{\partial w_{jq}^{(v)}} &=& \delta_j^{(v)} z_q^{(v-1)} \nonumber \\ \frac{\partial E_n}{\partial b_j^{(v)}} &=& \delta_j^{(v)} \nonumber \end{eqnarray}\] เมื่อ \(\delta_j^{(v)} = \hat{\delta}_j^{(v)} \cdot h'(a_j^{(v)})\) โดย \(h'(\cdot)\) เป็นอนุพันธ์ของฟังก์ชันกระตุ้นในชั้น \(v^{th}\).
ชั้น \(v^{th}\) คำนวณ \(\hat{\delta}_q^{(v-1)}\) เพื่อส่งย้อนไปให้ชั้น \((v-1)^{st}\) จากสมการ \(\eqref{eq: ANN BP delta j}\). นั่นคือ \[\hat{\delta}_q^{(v-1)} = \sum_j w_{jq}^{(v)} \delta_j^{(v)} \nonumber\] สำหรับ \(q = 1, \ldots, Q\) เมื่อ \(Q\) เป็นจำนวนเอาต์พุตทั้งหมดของชั้น \((v-1)^{st}\).
หากชั้น \((v-1)^{st}\) เป็นชั้นคอนโวลูชั่นหรือชั้นดึงรวม ต้องทำการรื้อฟื้นโครงสร้างกลับมาใหม่ นั่นคือ \[\hat{\delta}_{fkl}^{(v-1)} = \hat{\delta}_q^{(v-1)} \nonumber\] เมื่อ \(q = l + W' \cdot (k - 1) + H' W' \cdot (f - 1)\) สำหรับ \(q = 1, \ldots, F' \cdot H' \cdot W'\) โดย \(F', H', W'\) คือจำนวนลักษณะสำคัญ, ขนาดเอาต์พุตแนวตั้ง, ขนาดเอาต์พุตแนวนอนของชั้น \((v-1)^{st}\) ตามลำดับ.
6.4.1.0.3 กรณีชั้นดึงรวม
ที่กรณีชั้น \(v^{th}\) เป็นชั้นดึงรวม ชั้น \(v^{th}\) รับ \(\hat{\delta}_{frs}^{(v)}\) มาจากชั้น \((v+1)^{st}\). ชั้นดึงรวมไม่มีค่าน้ำหนัก ไม่จำเป็นต้องคำนวณเกรเดียนต์ แต่ชั้นดึงรวมต้องส่ง \(\hat{\delta}_{fkl}^{(v-1)}\) ไปให้ชั้น \((v-1)^{st}\). ค่า \(\hat{\delta}_{fkl}^{(v-1)}\) คำนวณได้จากสมการ \(\eqref{eq: deep conv grad delta hat next pooling}\). นั่นคือ \[\hat{\delta}_{fkl}^{(v-1)} = \sum_{r \in \Omega_r} \sum_{s \in \Omega_s} \hat{\delta}_{frs}^{(v)} \frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}} \nonumber\] สำหรับ \(f = 1, \ldots, F'\); \(k = 1, \ldots, H'\) และ \(l = 1, \ldots, W'\) เมื่อ \(\Omega_r = \Omega(k, S_H, H_F)\); \(\Omega_s = \Omega(l, S_W, W_F)\) และ \(F', H', W'\) คือจำนวนลักษณะสำคัญ, ขนาดเอาต์พุตแนวตั้ง, ขนาดเอาต์พุตแนวนอนของชั้น \((v-1)^{st}\) ตามลำดับ.
ฟังก์ชันเซตคำนวณได้จากสมการ \(\eqref{eq: deep conv back r set}\), \[\Omega(k, S, H) = \left\{ \frac{k - i}{S} + 1: (k - i \geq 0) \;\mathrm{and}\; \left( (k - i) \;\mathrm{mod}\; S = 0 \right) \right\}_{i = 1, \ldots, H} \nonumber .\]
ค่า \(\frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}}\) ขึ้นกับชนิดการดึงรวม. การดึงรวมแบบมากที่สุด ใช้สมการ \(\eqref{eq: deep conv grad max pool}\), \[\frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}} = \left\{ \begin{array}{l l} 1 & \;\mbox{เมื่อ}\; z_{fkl}^{(v-1)} = \max( \{ z_{f, S_H \cdot (r-1)+i, S_W \cdot (s-1)+j}^{(v-1)} \}_{i=1,\ldots, H_F, j=1,\ldots, W_F} ), \\ 0 & \;\mbox{อื่น ๆ}. \end{array} \right. \nonumber\]
การดึงรวมแบบเฉลี่ย ใช้สมการ \(\eqref{eq: deep conv grad average pool}\), \[\frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}} = \frac{1}{H_F W_F} \nonumber\] เมื่อ \(H_F \times W_F\) เป็นขนาดของฟิลเตอร์ชั้นที่ \(v^{th}\).
การดึงรวมแบบอาร์เอ็มเอส ใช้สมการ \(\eqref{eq: deep conv grad rms pool}\) \[\frac{\partial z_{frs}^{(v)}}{\partial z_{fkl}^{(v-1)}} = \frac{z_{fkl}^{(v-1)}}{H_F W_F \cdot z_{frs}^{(v)}} \nonumber\] เมื่อ \(H_F \times W_F\) เป็นขนาดของฟิลเตอร์ชั้นที่ \(v^{th}\).
6.4.1.0.4 กรณีชั้นคอนโวลูชั่น
ที่กรณีชั้น \(v^{th}\) เป็นชั้นคอนโวลูชั่น ชั้น \(v^{th}\) รับ \(\hat{\delta}_{qrs}^{(v)}\) มาจากชั้น \((v+1)^{st}\) และชั้น \(v^{th}\) คำนวณเกรเดียนต์เทียบกับน้ำหนักของชั้นจากสมการ \(\eqref{eq: deep conv grad E/w 2}\) และสมการ \(\eqref{eq: deep conv grad E/b}\). นั่นคือ
\[\begin{eqnarray} \frac{\partial E_n}{\partial w_{qfij}^{(v)}} &=& \sum_{r=1}^{H} \sum_{s=1}^{W} \delta_{qrs}^{(v)} z_{f, S_H \cdot (r-1)+i, S_W \cdot (s-1)+j}^{(v-1)} \nonumber \\ \frac{\partial E_n}{\partial b_q^{(v)}} &=& \sum_{r=1}^{H} \sum_{s=1}^{W} \delta_{qrs}^{(v)} \nonumber \end{eqnarray}\] สำหรับ \(q = 1, \ldots, F\); \(f = 1, \ldots, F'\); \(i = 1, \ldots, H_F\) และ \(j = 1, \ldots, W_F\) เมื่อ \(F, H_F, W_F\) เป็นจำนวนลักษณะสำคัญ ขนาดฟิลเตอร์แนวตั้ง ขนาดฟิลเตอร์แนวนอนของชั้น \(v^{th}\) ตามลำดับ, \(F'\) เป็นจำนวนลักษณะสำคัญของชั้น \((v-1)^{st}\), ค่า \(z_{f, S_H \cdot (r-1)+i, S_W \cdot (s-1)+j}^{(v-1)}\) คือ อินพุตของชั้น \(v^{th}\) ที่ผ่านการเติมเต็มแล้ว, \(S_H\) และ \(S_W\) เป็นค่าก้าวย่างตามแนวตั้งและนอนของชั้น \((v-1)^{st}\) และ \(\delta_{qrs}^{(v)} = \hat{\delta}_{qrs}^{(v)} \cdot h'(a_{qrs}^{(v)})\) โดย \(h'(a_{qrs}^{(v)})\) เป็นอนุพันธ์การกระตุ้นของชั้น \(v^{th}\).
ชั้น \(v^{th}\) คำนวณ \(\hat{\delta}_{fkl}^{(v-1)}\) เพื่อส่งย้อนไปให้ชั้น \((v-1)^{st}\) จากสมการ \(\eqref{eq: deep conv delta layer m 3}\). นั่นคือ
\[\begin{eqnarray} \hat{\delta}_{fkl}^{(v-1)} &=& \sum_{q=1}^F \sum_{r \in \Omega_r} \sum_{s \in \Omega_s} \delta_{qrs}^{(v)} \cdot w_{q,f,k-S_H \cdot (r - 1),l-S_W \cdot (s - 1)}^{(v)} \nonumber \end{eqnarray}\] สำหรับ \(f = 1, \ldots, F'\); \(k = 1, \ldots, H'\) และ \(l = 1, \ldots, W'\) เมื่อ \(\Omega_r = \Omega(k, S_H, H_F)\); \(\Omega_s = \Omega(l, S_W, W_F)\); \(F, H_F, W_F, S_H, S_W\) คือจำนวนลักษณะสำคัญ ขนาดฟิลเตอร์ตามแนวตั้ง ขนาดฟิลเตอร์ตามแนวนอน ขนาดก้าวย่างตามแนวตั้ง ขนาดก้าวย่างตามแนวนอนของชั้น \(v^{th}\) ตามลำดับ, \(F', H', W'\) คือจำนวนลักษณะสำคัญ, ขนาดเอาต์พุตแนวตั้ง, ขนาดเอาต์พุตแนวนอนของชั้น \((v-1)^{st}\) ตามลำดับ และ จากสมการ \(\eqref{eq: deep conv back r set}\), \(\Omega(k, S, H) = \{ \frac{k - i}{S} + 1: (k - i \geq 0) \;\mathrm{and}\; \left( (k - i) \;\mathrm{mod}\; S = 0 \right) \}_{i = 1, \ldots, H}\).
6.4.1.0.5 พารามิเตอร์ที่นิยม.
แม้ว่าปัจจุบันอาจจะยังไม่มีทฤษฎีที่ศึกษาอย่างดีรับรองการเลือกพารามิเตอร์ต่าง ๆ แต่ค่าพารามิเตอร์ที่นิยมใช้สำหรับโครงข่ายคอนโวลูชั่น ได้แก่ สำหรับชั้นคอนโวลูชั่น นิยมใช้กับ ฟิลเตอร์ขนาดเป็น \(3 \times 3\) หรือ \(5 \times 5\) และขนาดก้าวย่างเป็น \(1 \times 1\). สำหรับชั้นดึงรวม นิยมใช้กับ ฟิลเตอร์ขนาดเป็น \(2 \times 2\) หรือ \(3 \times 3\) และขนาดก้าวย่างเป็น \(2 \times 2\).
6.5 โครงข่ายคอนโวลูชั่นที่สำคัญ
การออกแบบโครงสร้างของโครงข่ายคอนโวลูชั่นในปัจจุบัน นิยมทำด้วยมุุมมอง การกำหนดสาระสำคัญในระดับสูง (high level of abstraction). นั่นคือ คล้ายกับการออกแบบวงจรอิเลกทรอนิกส์ ที่หากไม่ได้ต้องการคุณสมบัติอะไรพิเศษมากนัก แทนที่จะออกแบบวงจร โดยเลือกอุปกรณ์พื้นฐาน เช่น ทรานซิสเตอร์ ตัวต้านทาน ตัวเก็บประจุ ไดโอด รีเลย์ และการเชื่อมต่อระหว่างอุปกรณ์พื้นฐานเหล่านี้ ปัจจุบันการออบแบบวงจร นิยมเริ่มจากการเลือกวงจรรวมก่อน แล้วค่อยเสริม ประกอบ หรือดัดแปลง ให้เข้ากับความต้องการ.
เช่นเดียวกัน การออกแบบโครงสร้างของโครงข่ายคอนโวลูชั่นในปัจจุบัน ก็นิยมเริ่มจากโครงข่ายคอนโวลูชั่นที่รู้จักกันดีแล้ว และดัดแปลงตามความเหมาะสม. หัวข้อต่อไปนี้ อภิปรายตัวอย่างของโครงข่ายคอนโวลูชั่นเด่น ๆ ที่รู้จักกันดี และนิยมถูกเลือกมาเป็นจุดเริ่มต้นของโครงสร้าง เช่น อเล็กซ์เน็ต, วีจีจีเน็ต, อินเซปชั่น, เรสเน็ต, และเดนซ์เน็ต.
6.5.1 อเล็กซ์เน็ต
อเล็กซ์เน็ต (AlexNet) เป็นโครงข่ายคอนโวลูชั่น ที่ได้รับความสนใจอย่างมาก หลังจากชนะการแข่งขันจำแนกชนิดวัตถุในภาพถ่าย อิมเมจเนต (ImageNet) ในปี 2012 (ชุดข้อมูลมักถูกอ้างอิงว่า ImageNet LSVRC-2012).
อเล็กซ์เน็ตเป็นงานแรก ๆ ที่แสดงความสามารถการทำนายจากเครื่อง ที่ใกล้เคียงกับระดับของมนุษย์ได้. การแข่งขัน 5 ทดสอบผลด้วย ภาพถ่าย \(100,000\) ภาพ ที่แต่ละภาพมีฉลากเฉลยของชนิดวัตถุในภาพ. ชุดข้อมูลครอบคลุมถึง \(1000\) ชนิดวัตถุ. ผลตัดสินวัดจากค่าผิดพลาดของห้าชนิดอันดับสูงสุด (top-5 error rate) ซึ่งอเล็กซ์เน็ตทำได้ต่ำถึง \(15.3\%\). หมายเหตุ ค่าผิดพลาดของห้าชนิดอันดับสูงสุด หมายถึง อัตราการทายผิด ซึ่งคือ อัตราส่วน จำนวนตัวอย่างที่ฉลากเฉลยไม่อยู่ในห้าชนิดอันดับแรกสุดที่ทาย ต่อจำนวนตัวอย่างทั้งหมด.
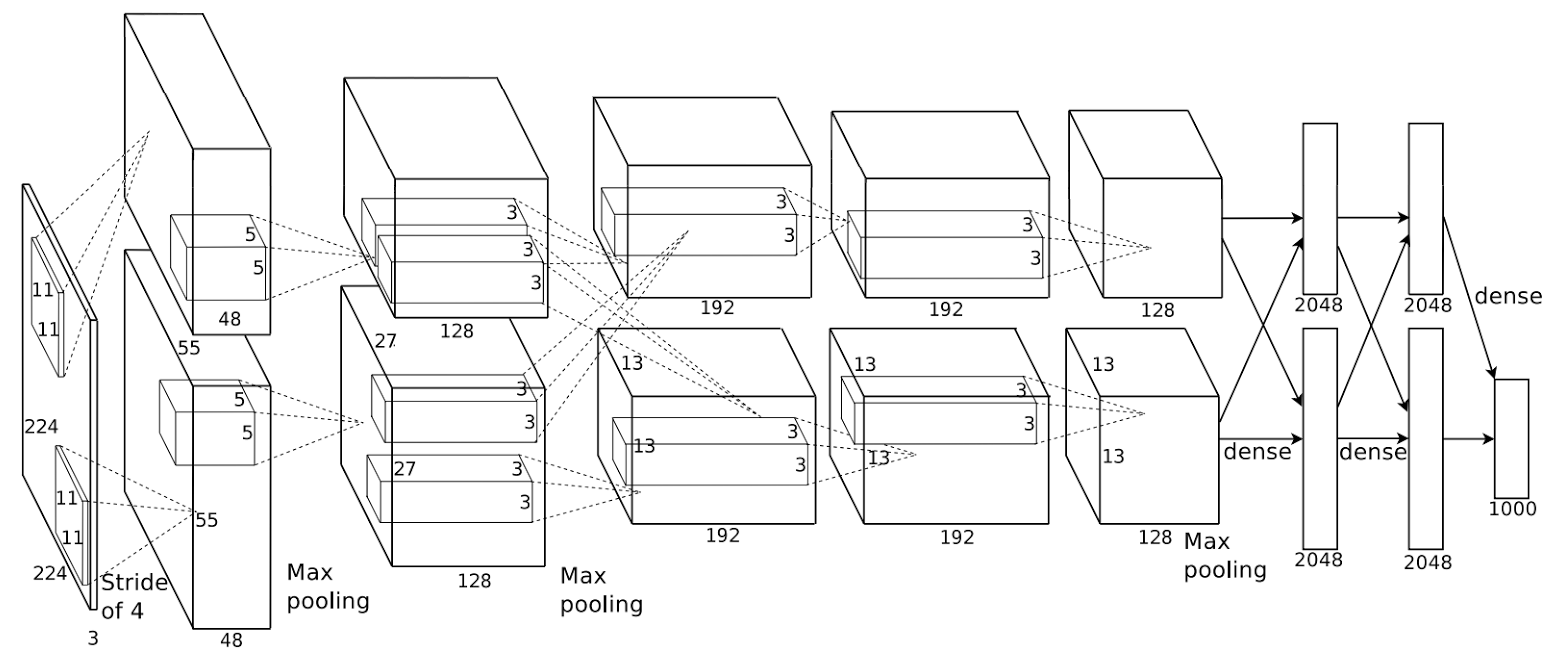
อเล็กซ์เน็ตใช้ชั้นคอนโวลูชั่น \(5\) ชั้น แล้วตามด้วยชั้นเชื่อมต่อเต็มที่ \(3\) ชั้น รวมแล้วใช้ พารามิเตอร์ราว \(60\) ล้านตัว. อเล็กซ์เน็ต ใช้เรลูเป็นฟังก์ชันกระตุ้น เพื่อช่วยให้การเรียนรู้ทำได้ง่ายขึ้น และใช้กลไกตกออก เพื่อลดปัญหาโอเวอร์ฟิตติ้ง. ที่สำคัญคือ อเล็กซ์เน็ต ใช้การประมวลผลจีพียูอย่างมีประสิทธิภาพ. อเล็กซ์เน็ตถูกฝึกกับตัวอย่างภาพร่วม \(1.2\) ล้านภาพ (จากชุดข้อมูลอิมเมจเนต ของปี 2010 หรือ LSVRC-2010).
โครงสร้างของอเล็กซ์เน็ต แสดงดังรูป 1.23. โครงสร้างของอเล็กซ์เน็ต แยกการคำนวณออกเป็นสองเส้นทาง เพื่อแก้ปัญหาขนาดความจำ โดยใช้การ์ดประมวลผลจีพียูสองการ์ดร่วมกัน. การคำนวณของชั้นเชื่อมต่อเต็มที่ แม้จะแบ่งส่วนคำนวณ (กระจายภาระทางฮาร์ดแวร์) แต่การนำผลลัพธ์มารวมกันทำให้ผลลัพธ์ที่ได้เสมือนกับว่าไม่มีการแบ่งส่วน.
6.6 อภิธานศัพท์
- โครงข่ายคอนโวลูชั่น (convolution neural network):
โครงข่ายประสาทเทียมที่มีการใช้ชั้นคอนโวลูชั่น.
- ชั้นคอนโวลูชั่น (convolution layer):
ชั้นคำนวณที่อาศัยกลไกการเชื่อมต่อท้องถิ่นและการใช้ค่าน้ำหนักร่วม.
- ฟิลเตอร์ (filter):
ชุดค่าน้ำหนักของชั้นคอนโวลูชั่น อาจเรียกว่า เคอร์เนล.
- เคอร์เนล (kernel):
ชุดค่าน้ำหนักของชั้นคอนโวลูชั่น อาจเรียกว่า ฟิลเตอร์.
- การเติมเต็มด้วยศูนย์ (zero-padding):
การขยายมิติของอินพุตของชั้นคอนโวลูชั่น ด้วยการเพิ่มมิติที่มีค่าเป็นศูนย์เข้าไป โดยมักมีจุดประสงค์ เพื่อควบคุมขนาดของเอาต์พุตของชั้นคอนโวลูชั่น
- ขนาดก้าวย่าง (stride):
ขนาดการขยับตำแหน่งของอินพุต เพื่อนำมาคำนวณเอาต์พุตหน่วยถัดไป.
- แผนที่ลักษณะสำคัญ (feature map):
เอาต์พุตจากชั้นคอนโวลูชั่น
- ชั้นดึงรวม (pooling layer):
ชั้นคำนวณ ที่สรุปสถิติของบริเวณท้องถิ่นต่าง ๆ ของอินพุตออกมา.
- ชั้นเชื่อมต่อเต็มที่ (fully connected layer):
ชั้นคำนวณโครงข่ายประสาทเทียมแบบดั้งเดิม (นั่นคือ ไม่คำนึงถึงโครงสร้างมิติของอินพุต และไม่มีโครงสร้างมิติของเอาต์พุต).