5 แบบฝึกหัด

“For any scientist, the real challenge is not to stay within the secure garden of the known but to venture out into the wilds of the unknown.”

—Marcus Du Sautoy

“สำหรับนักวิทยาศาสตร์ ความท้าทายจริง ๆ ไม่ใช่การพักอยู่ภายในสวนที่ปลอดภัยของสิ่งที่รู้ แต่เป็นการท่องออกไปในป่าของความไม่รู้.”

—มาร์คัส ดู โซวทอย

5.0.0.0.1 แบบฝึกหัด

จงศึกษาตัวอย่างและแสดงปัญหาการเลือนหายของเกรเดียนต์ พร้อมเปรียบเทียบผลลัพธ์จากการบรรเทา โดยเปลี่ยนมาใช้ฟังก์ชันกระตุ้นเรลู.

ตัวอย่างข้อมูลงานจำแนกประเภทเพื่อแสดงปัญหาการเลือนหายของเกรเดียนต์. ข้อมูลสร้างจาก จุดข้อมูลที่ i^{th} ของกลุ่ม c นั่นคือ \boldsymbol{x}_c(i) = [r_c(i) \cdot \sin \theta_c(i), r_c(i) \cdot \cos \theta_c(i)]^T โดย c เป็นดัชนีของกลุ่ม และทุก ๆ กลุ่มมี r_c(i) = (i-1)/N กับ \theta_c(i) = (i-1) \cdot \frac{4 \pi}{3 N} + c \cdot \frac{2 \pi}{3} + \epsilon สำหรับ i \in \{1, \ldots, N\} และ N คือจำนวนจุดข้อมูลของแต่ละกลุ่ม. ส่วนสัญญาณรบกวน \epsilon \sim \mathcal{N}(0, 0.2). — ตัวอย่างข้อมูลงานจำแนกประเภทเพื่อแสดงปัญหาการเลือนหายของเกรเดียนต์. ข้อมูลสร้างจาก จุดข้อมูลที่ $i^{th}$ ของกลุ่ม $c$ นั่นคือ $\boldsymbol{x}_c(i) = [r_c(i) \cdot \sin \theta_c(i), r_c(i) \cdot \cos \theta_c(i)]^T$ โดย $c$ เป็นดัชนีของกลุ่ม และทุก ๆ กลุ่มมี $r_c(i) = (i-1)/N$ กับ $\theta_c(i) = (i-1) \cdot \frac{4 \pi}{3 N} + c \cdot \frac{2 \pi}{3} + \epsilon$ สำหรับ $i \in \{1, \ldots, N\}$ และ $N$ คือจำนวนจุดข้อมูลของแต่ละกลุ่ม. ส่วนสัญญาณรบกวน $\epsilon \sim \mathcal{N}(0, 0.2)$.

ตัวอย่างเช่น (1) เขียนโปรแกรมเพื่อสร้างข้อมูล. รูป 1 แสดงตัวอย่างข้อมูล ¹ ที่เป็นปัญหาการจำแนกกลุ่ม โดยอินพุตมี $2$ มิติ และเอาต์พุตเป็นชนิดมี $3$ ชนิด ซึ่งสร้างจากตัวอย่างคำสั่งข้างล่าง

N = 100
X = np.zeros((2, N*3))                # Initialize dummy input
y = np.zeros((1, N*3), dtype='uint8') # Initialize dummy output
sec = 2*np.pi/3

for k in range(3):
    ix = range(N*k,N*(k+1))  ## Indices of class k
    r = np.linspace(0.0,1,N) ## Radius
    t = np.linspace(k*sec,(k+2)*sec, N) + np.random.randn(N)*0.2 
    X[:, ix] = np.c_[r*np.sin(t), r*np.cos(t)].T   
    y[0, ix] = k

หมายเหตุ ไม่จำเป็นต้องสร้างข้อมูลตามตัวอย่างในรูป.

จากนั้น (2) ทดลองสร้าง ฝึก และทดสอบโครงข่ายประสาทเทียมความลึกต่าง ๆ โดยเพิ่มความลึกขึ้นเรื่อยๆ และสังเกตความยากของการฝึก. ดูหัวข้อ [sec: relu] ประกอบ. (ตัวอย่างโปรแกรม ศึกษาได้จากหัวข้อ [sec: ann exercises].)

สุดท้าย (3) ทดลองเปลี่ยนฟังก์ชันกระตุ้นเป็นเรลู (ตัวอย่างโปรแกรมการคำนวณเรลู แสดงในรายการ [code: svm primal gd].) สังเกตผล เปรียบเทียบ และอภิปราย.

5.0.0.0.2 แบบฝึกหัด

จากแบบฝึกหัด 1.0.0.0.1 ตั้งสมมติฐานถึงสาเหตุของปัญหาการฝึกโครงข่ายประสาทเทียมลึก ออกแบบการทดลอง เพื่อพิสูจน์และศึกษาสมมติฐานนั้น ดำเนินการทดลอง สังเกตผล วิเคราะห์ สรุป วิจารณ์และอภิปราย. ศึกษาและทดลองทั้งฟังก์ชันกระตุ้นซิกมอยด์ และเรลู พร้อมสังเกตขนาดเกรเดียนต์ที่ชั้นต่าง ๆ ขณะฝึก. อภิปรายถึงสาเหตุอื่นที่อาจเป็นไปได้ นอกจากขนาดของเกรเดียนต์. ดูรูป 4 และผลในหัวข้อ [sec: relu] ประกอบ.

รายการ [code: class ANN] แสดงโปรแกรมโครงข่ายประสาทเทียมที่ปรับปรุงใหม่ โดยเขียนอยู่ในรูปแบบโปรแกรมเชิงวัตถุ และที่เมท็อด train มีอาร์กิวเมนต์ track_grad ที่สามารถสั่งให้เก็บขนาดของเกรเดียนต์ไว้เพื่อตรวจสอบภายหลังได้. ตัวอย่างคำสั่งข้างล่าง ฝึกและทดสอบโครงข่ายสามชั้น (จำนวนหน่วยซ๋อนเป็น $4$ และ $8$ ชั้นตามลำดับ) สำหรับข้อมูล datax และ y_onehot ที่อินพุตมีขนาดสองมิติและเอาต์พุตอยู่ในรูปแบบรหัสหนึ่งร้อน สำหรับงานจำแนกกลุ่มที่มีสามกลุ่ม โดยมีจำนวนข้อมูลฝึกเป็น $300$ จุดข้อมูล

net = w_initn([2, 4, 8, 3])
net['act1'] = sigmoid
net['act2'] = sigmoid
net['act3'] = softmax
ann = ANN(net, NB=300, shuffle='once')

# Train net
train_losses, maggrads = ann.train(datax, y_onehot, cross_entropy, 
lr=0.3/300, epochs=500, track_grad=True)

yp = ann.predict(testx)
yc = np.argmax(yp, axis=0)  
accuracy = np.mean(yc == testy[0,:])
print('Test accuracy: ', accuracy)

เมื่อ testx และ testy เป็นอินพุตและเอาต์พุตของข้อมูลทดสอบ และเฉลย testy ระบุฉลากที่ถูกต้องของจุดข้อมูล. โปรแกรม w_initn, sigmoid, softmax, และ cross_entropy แสดงในรายการ [code: w_initn], [code: sigmoid], [code: softmax] และ [code: cross entropy] ตามลำดับ. โปรแกรม cross_entropy ในรายการ [code: cross entropy] คำนวณผลรวมของค่าฟังก์ชันสูญเสียต่อจุดข้อมูลออกมา การกำหนดค่าอัตราการเรียนรู้ lr=0.3/300 ให้ผลในการฝึก เสมือนว่าค่าน้ำหนักถูกปรับจากค่าเฉลี่ยของค่าฟังก์ชันสูญเสียต่อจุดข้อมูล ด้วยอัตราการเรียนรู้ $0.3$. นั่นคือ $w - (\alpha/N) \cdot \sum_n \nabla E$ $\equiv$ $w - \alpha \cdot \frac{1}{N} \sum_n \nabla E$. แม้ว่าผลจริงไม่ได้แตกต่างกัน แต่การใช้ค่าเฉลี่ย (ในวิธีที่แสดงนี้) ช่วยให้การเลือกอัตราเรียนรู้ทำได้สะดวกขึ้น. ค่าอัตราเรียนรู้ สามารถเลือกได้โดยไม่ต้องคำนึงถึงจำนวนจุดข้อมูลฝึก.

หมายเหตุ นอกจากการเขียนในรูปโปรแกรมเชิงวัตถุ และเพิ่ม track_grad แล้ว ส่วนหนึ่งที่สำคัญคือ โปรแกรมในรายการ [code: class ANN] ได้เตรียมความสามารถในการฝึกหมู่เล็ก (หัวข้อ [sec: minibatch]) ซึ่งการฝึกหมู่เล็ก ไม่ใช่จุดประสงค์ของแบบฝึกหัดนี้ และ ดังเช่นที่แสดงในตัวอย่างคำสั่งข้างต้น สามารถกำหนดให้ทำการฝึกแบบหมู่ ได้โดยการกำหนดจำนวนหมู่เล็ก เท่ากับ(หรือมากกว่า) จำนวนของจุดข้อมูลฝึก ดังเช่น

ann = ANN(net, NB=300, shuffle='once')

เมื่อ $300$ คือจำนวนจุดข้อมูลฝึก.

class ANN:
    def __init__(self, net_params, NB=16, shuffle='once'):
        '''
        NB: minibatch size
        shuffle: 'none'=no shuffle, 'once', 'often'=every epoch
        net_params: weights, biases, and activation functions
        '''
        self.NB = NB
        self.shuffle = shuffle
        self.net_params = net_params
        self.NB_ids = None
        self.NMB = None

    def prepare_minibatches(self, N):
        if self.NB > N:
            self.NB = N

        self.NMB = int(N/self.NB)   # a number of minibatches   
        self.NB_ids = np.arange(N)
        if self.shuffle != 'none':
            np.random.shuffle(self.NB_ids)

    def getbatch(self, i, X, Y):
        if i == 0 and self.shuffle == 'often':
            np.random.shuffle(self.NB_ids)
        bids = i * self.NB
        eids = bids + self.NB
        ids = self.NB_ids[bids:eids]
        return X[:, ids], Y[:, ids]

    def train(self, trainX, trainY, loss, lr=0.1, epochs=1000, 
            track_grad=False, term=1e-8, term_count_max=5):
        num_layers = self.net_params['layers']    
        last_layer = num_layers-1

        out_act = 'act%d'%last_layer    
        _, N = trainX.shape    
        A = {}
        Z = {}
        delta = {}
        dEw = {}
        dEb = {}
        train_losses = []    
        term_count = 0

        # Minibatch
        self.prepare_minibatches(N)

        step_size = lr
        if track_grad:
            magGrad = {}
            for i in range(1, num_layers):
                magGrad['dEw%d'%i] = []
                magGrad['dEb%d'%i] = []

        for nt in range(epochs):               
            for ib in range(self.NMB):
                Z[0], batchY = self.getbatch(ib, trainX, trainY)    
                # (1) Forward pass
                for i in range(1, num_layers):
                    b = self.net_params['bias%d'%i]
                    w = self.net_params['weight%d'%i]
                    act_f = self.net_params['act%d'%i]
                    A[i] = np.dot(w, Z[i-1]) + b    # A: M x N
                    Z[i] = act_f(A[i])              # Z: M x N
                # end forward pass
                Yp = Z[i]

                # (2) Calculate output dE/da
                delta[last_layer] = Yp - batchY  # delta: M x N

                # (3) Backpropagate: calc. dE/da for layer i-1
                for i in range(last_layer, 1, -1):
                    b = self.net_params['bias%d'%i]   # Mnxt,1 
                    w = self.net_params['weight%d'%i] # Mnxt,M
                    act_f = self.net_params['act%d'%(i-1)]

                    sumdw = np.dot(w.transpose(), delta[i]) #M,N
                    if act_f == sigmoid:
                        delta[i - 1] = dsigmoid(Z[i - 1]) * sumdw 
                    elif act_f == relu:
                        delta[i - 1] = drelu(A[i - 1]) * sumdw 
                    else:
                        assert act_f == sigmoid or act_f == relu

                    # (4) Calculate gradient dE/dw and dE/db
                    dEw[i] =np.dot(delta[i],Z[i-1].transpose())    
                    dEb[i] =np.dot(delta[i],np.ones((self.NB,1))) 
                    if track_grad:
                        magE = np.mean(np.abs(dEw[i]))
                        magB = np.mean(np.abs(dEb[i]))
                        magGrad['dEw%d'%i].append(magE)
                        magGrad['dEb%d'%i].append(magB)                
                # end backpropagate

                # Calculate gradient dE/dw and dE/db
                dEw[1] = np.dot(delta[1], Z[0].transpose()) 
                dEb[1] = np.dot(delta[1], np.ones((self.NB, 1))) 

                if track_grad:
                    magE = np.mean(np.abs(dEw[1]))
                    magB = np.mean(np.abs(dEb[1]))
                    magGrad['dEw1'].append(magE)
                    magGrad['dEb1'].append(magB)                

                # Update parameters w/ Gradient Descent
                gnorm = 0
                for i in range(1, num_layers):
                    b = self.net_params['bias%d'%i]
                    w = self.net_params['weight%d'%i]
                    b -= step_size * dEb[i]
                    w -= step_size * dEw[i]
                    
                    gnorm += np.linalg.norm(dEb[i])
                    gnorm += np.linalg.norm(dEw[i])                    
                # end update parameters
                
                # Calculate loss at each batch
                lossn = np.sum(loss(Yp, batchY), axis=0) 
                train_losses.append(np.mean(lossn))      

                # Check termination condition
                if gnorm < term:
                    term_count += 1
                    
                    if term_count > term_count_max:
                        print('Reach term. at %d(%d)'%(nt, ib))                        
                        if track_grad:
                            return train_losses, magGrad
                        return train_losses # losses per batches                         
                else: # reset term_count
                    term_count = 0
                # end if term_count
            # end ib
        # end epoch nt

        if track_grad:
            return train_losses, magGrad
        return train_losses # losses per batches 

    def predict(self, X):
        num_layers = self.net_params['layers']
        Z = X        
        for i in range(1, num_layers):            
            b = self.net_params['bias%d'%i]
            w = self.net_params['weight%d'%i]
            act_f = self.net_params['act%d'%i]
            A = np.dot(w, Z) + b    # A: M x N
            Z = act_f(A)            # Z: M x N
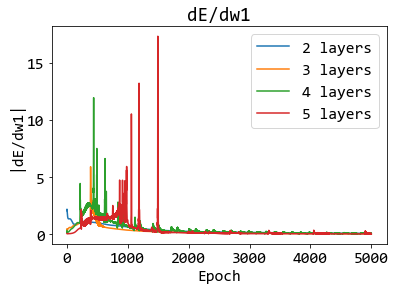
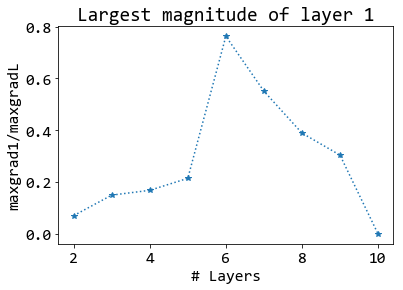
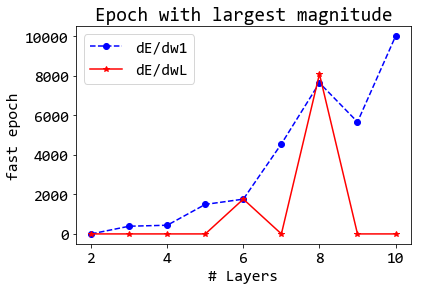
        return Z # M x N

รูป 4 แสดงตัวอย่างการนำเสนอผล. จากผลที่แสดงในรูป 4 อาจอภิปราย ได้ดังนี้ (1) ภาพกลางแสดงในเห็นชัดเจนว่า ส่วนใหญ่ขนาดของเกรเดียนต์ในชั้นแรก น้อยกว่าชั้นสุดท้าย และน้อยกว่ามากๆ โดยส่วนใหญ่. แต่แนวโน้ม ไม่ได้เป็นไปในทางเดียว นั่นคือ พบขนาดเกรเดียนต์ในชั้นแรกที่ใหญ่ที่สุด เมื่อใช้ความลึก $6$ ชั้น (ซึ่งมีขนาดถึงเกือบ $0.8$ หรือเกือบ $80\%$ ของขนาดเกรเดียนต์ชั้นสุดท้าย) และผลลัพธ์แสดงการลดลงในทั้งสองทิศทาง โดยที่ความลึกสิบชั้น ขนาดเกรเดียนต์ในชั้นแรกมีค่าต่ำมากเมื่อเทียบกับชั้นสุดท้าย. (2) ภาพซ้าย และภาพขวา แสดงสาเหตุในเห็นอีกมุมหนึ่ง คือไม่ใช่แค่ขนาดที่น้อยอย่างเดียว แต่เป็น เมื่อไรที่ชั้นคำนวณต้น ๆ จะได้เกรเดียนต์ขนาดใหญ่. ภาพซ้าย แสดงให้เห็นว่า เกรเดียนต์ชั้นแรกที่มีขนาดใหญ่จะมาช้าลง ในโครงข่ายที่ลึกขึ้น. ภาพขวา ยืนยันเรื่องที่เกรเดียนต์ขนาดใหญ่มาช้า ในโครงข่ายลึก. สังเกตว่า ชั้นสุดท้าย (เส้นหนาสีแดง) จะเห็นเกรเดียนต์ขนาดใหญ่ที่สุด ในสมัยฝึกต้นๆ (เห็นเร็ว) แทบจะทุกระดับความลึก (ยกเว้นความลึก $8$). แต่ชั้นแรก (เส้นประสีน้ำเงิน) จะเห็นเกรเดียนต์ขนาดใหญ่ที่สุด ช้าลงเรื่อยๆ (สมัยฝึกสูง) เมื่อความลึกเพิ่มขึ้นเรื่อยๆ โดยแนวโน้มแทบจะเป็นลำดับทางเดียว (monotonic). การที่เห็นเกรเดียต์ขนาดใหญ่ช้า อาจหมายถึง การปรับค่าน้ำหนักของชั้นได้ช้าด้วย ซึ่งตีความได้ว่า การใช้โครงข่ายที่ลึกนั้น ต้องการการฝึกที่ยาวนานขึ้น และการฝึกที่ยาวนานขึ้น โดยทั่วไปแล้ว หมายถึง การฝึกที่ยาก.

ปัญหาการเลือนหายของเกรเดียนต์. ภาพซ้าย แสดงขนาดเฉลี่ยของเกรเดียนต์ชั้นที่หนึ่ง ต่อสมัยฝึก ของโครงข่ายประสาทเทียมความลึกต่าง ๆ. ภาพกลาง แสดงอัตราส่วนระหว่างขนาดที่ใหญ่ที่สุดจากเกรเดียนต์ชั้นที่หนึ่ง กับขนาดที่ใหญ่ที่สุดจากเกรเดียนต์ชั้นสุดท้าย เมื่อใช้ความลึกต่าง ๆ. ภาพขวา แสดงสมัยฝึกที่เกรเดียนต์มีขนาดใหญ่ที่สุด ของชั้นแรก และชั้นสุดท้าย เมื่อใช้ความลึกต่าง ๆ.

5.0.0.0.3 แบบฝึกหัด

จากแบบฝึกหัด 1.0.0.0.1 และ 1.0.0.0.2 ออกแบบการทดลอง เพื่อวัดผลการแก้ปัญหาการฝึกโครงข่ายลึก และผลการบรรเทาปัญหาการเลือนหายของเกรเดียนต์ เมื่อใช้ฟังก์ชันกระตุ้นเรลู เปรียบเทียบกับซิกมอยด์ ดำเนินการทดลอง สังเกต วัดผล สรุปและนำเสนอผลให้ชัดเจน ทั้งประเด็นใหญ่ (การฝึกโครงข่ายลึก) และประเด็นย่อย (การเลือนหายของเกรเดียนต์).

5.0.0.0.4 แบบฝึกหัด

จากหัวข้อ [sec: minibatch] ออกแบบการทดลอง เพื่อศึกษาผลของขนาดหมู่เล็ก ต่อเวลาในการฝึก ความยากง่ายในการฝึก และคุณภาพการฝึก โดยมีปัจจัยประกอบคือ (1) ความลึกของโครงข่ายประสาทเทียม และ (2) จำนวนข้อมูลฝึก. เลือก (หรือสร้าง) ข้อมูลขึ้นมา ดำเนินการทดลอง สังเกตและบันทึกผล สรุปและอภิปราย.

ด้วยข้อมูลที่มีเพิ่มมากขึ้น ชุดข้อมูลที่มีขนาดใหญ่มากๆ อาจพบการฝึกแบบหมู่เล็กที่ทำเพียงสมัยเดียว หรือแม้แต่บางครั้งอาจจะไม่สามารถฝึกได้ครบทุกหมู่เล็ก (ไม่ครบสมัย และไม่ได้เห็นข้อมูลครบทั้งหมด). สำหรับชุดข้อมูลที่มีขนาดใหญ่มากๆ อาจพบปัญหาประสิทธิภาพของการคำนวณ และหากเลือกใช้ข้อมูลเพียงบางส่วน อาจเกิดปัญหาการอันเดอร์ฟิตได้. อภิปราย ประเด็นการทำงานกับข้อมูลขนาดใหญ่มาก และศึกษาเพิ่มเติมจากบทความวิจัยต่าง ๆ.

5.0.0.1 ไพทอร์ช.

โปรแกรมการเรียนรู้เชิงลึก สามารถเขียนด้วยนัมไพได้ แต่เนื่องจากการประยุกต์ใช้ที่เด่นๆ ข้องเกี่ยวกับข้อมูลที่มีมิติและจำนวนมหาศาล การคำนวณด้วยจีพียู จะช่วยการทำงานกับข้อมูลเหล่านั้นให้เสร็จได้เร็วขึ้นมาก. หัวข้อนี้ แนะนำมอดูลไพทอร์ช (PyTorch) ซึ่งเป็นหนึ่งในเครื่องมือที่นิยมใช้กับการเรียนรู้เชิงลึก. มอดูลไพทอร์ช ช่วยอำนวยความสะดวก ตั้งแต่การย้ายการคำนวณไปทำที่จีพียู การหาค่าเกรเดียนต์อัตโนมัติ ไปจนถึงโปรแกรมสำเร็จรูปสำหรับกลไกการเรียนรู้เชิงลึกเด่น ๆ ซึ่งจะช่วยให้การใช้งาน และการเรียนรู้การเรียนรู้เชิงลึกทำได้สะดวกมากยิ่งขึ้น.

อย่างไรก็ตาม ถึงแม้ไพทอร์ช จะได้เตรียมโปรแกรมสำเร็จต่าง ๆ ไว้ให้ แต่การได้เขียนโปรแกรมจากปฏิบัติการพื้นฐานขึ้นเอง ก็ยังเป็นกระบวนการเรียนรู้ที่สำคัญ ที่ช่วยให้เข้าใจอย่างแท้จริง. ดังนั้น การดำเนินเนื้อหาจะเป็นลักษณะเช่นเดิม นั่นคือ เริ่มจากการเขียนโปรแกรมกลไกต่าง ๆ ขึ้นเอง จากปฏิบัติการพื้นฐาน แล้วค่อยทดลองใช้เครืื่องมือสำเร็จที่มี ในลักษณะค่อย ๆ ขยับทีละขั้น เพื่อสร้างทั้งความเข้าใจ ความคุ้นเคย และสำคัญไม่แพ้กันคือ ความมั่นใจ.

การติดตั้งไพทอร์ช แนะนำให้ศึกษาจากเวป https://pytorch.org/ โดยหากระบบมีจีพียู และยังไม่ได้เตรียมการใช้งาน แนะนำให้ติดตั้งและเตรียมการใช้งานจีพียู ก่อนติดตั้งไพทอร์ช. หลังติดตั้งเรียบร้อย เช่นเดียวกับการใช้งานโมเดูลเพิ่มเติมอื่น ๆ เราต้องนำเข้า มอดูลไพทอร์ชก่อน ด้วยคำสั่งเช่น import torch เมื่อนำเข้าสมบูรณ์ สามารถทดสอบง่าย ๆ ได้โดยการตรวจสอบเวอร์ชั่นของไพทอร์ช เช่น

>>> print(torch.__version__)
1.0.0

ซึ่ง 1.0.0 คือเวอร์ชั่นที่ใช้² หากไพทอร์ชที่ติดตั้งเป็นเวอร์ชั่นอื่นก็จะได้ค่าอื่นออกมา.

รายการ [code: activation functions torch] แสดงโปรแกรมฟังก์ชันกระตุ้นเรลู ซอฟต์แมกซ์ และครอสเอนโทรปี พร้อมฟังก์ชันกำหนดค่าเริ่มต้น ซึ่งทั้งหมดเปลี่ยนเครื่องมือจากนัมไพมาเป็นไพทอร์ช. หมายเหตุ ฟังก์ชันครอสเอนโทรปี ใช้ eps เป็นกลไกในการลดปัญหาการคำนวณเชิงเลข. นั่นคือ กรณีที่ค่าที่ทายเป็นศูนย์ สำหรับเฉลยเป็นหนึ่ง (ทายผิดมากๆ อาจเกิดตอนเริ่มต้น) จะทำให้เกิด $-\log(0) \rightarrow \infty$ . กรณีเช่นนี้ จะทำให้การคำนวณพัง และไม่สามารถคำนวณต่อไปได้. กลไกในการแก้คือใช้ค่าเล็กๆ เติมเข้าไป $-\log(0 + \epsilon) \rightarrow v_{\max}$ ซึ่ง $v_{\max}$ คือค่ามากที่สุด ($\approx 103$) เท่าที่ -torch.log จะสามารถคำนวณได้ก่อนจะให้ค่าออกมาเป็น inf. ค่า 1e-45 ที่เลือกใช้ มาจากค่าบวกที่เล็กที่สุด ที่เลขทศนิยมขนาดสามสิบสองบิตจะแทนได้ ซึ่งตัวเลขนี้จะต่างจาก 1e-323 ในรายการ [code: cross entropy] ที่สำหรับเลขทศนิยมขนาดหกสิบสี่บิต ซึ่งเป็นข้อมูลดีฟอล์ตของนัมไพ. รายการ [code: class ANN torch] แสดงโปรแกรมคำนวณโครงข่ายประสาทเทียม ด้วยไพทอร์ช. สังเกตว่า การสร้างเทนเซอร์ใหม่ จะมีการกำหนด device ด้วย ซึ่ง การกำหนดนี้จะช่วยให้เราสามารถเปลี่ยนการคำนวณระหว่าง ซีพียู และจีพียูได้สะดวกขึ้น. ดูแบบฝีกหัด [ex: torch mnist GPU] สำหรับการคำนวณด้วยจีพียู.

def trelu(a):
    return a.clamp(min=0)

def tdrelu(a):
    g = torch.ones(a.shape, device=a.device)
    g[a < 0] = 0
    return g

def tcross_entropy(yhat, y):
    assert yhat.shape == y.shape
    eps = 1e-45    
    v = -torch.log(torch.sum(y * yhat, dim=0) + eps)
    return v.reshape((1,-1))

def tsoftmax(va):
    assert va.shape[0] > 1, 'va must be in K x N.'    
    amax = torch.max(va, dim=0)[0]
    expa = torch.exp(va - amax)
    denom = torch.sum(expa, dim=0)
    return expa/denom
    
def tw_initn1(Ms, umeansigma=(0,1), dev=torch.device('cpu')):
    assert len(Ms) >= 2, 'Ms: #units, e.g., M = [2, 8, 3]'    
    num_layers = len(Ms)
    params = {'layers': num_layers}    
    mu = umeansigma[0]
    sigma = umeansigma[1]   
    for i, m in enumerate(Ms[1:], start=1):
        mprev = Ms[i-1]
        b = torch.randn((m,1), device=dev)
        w = torch.randn((m,mprev), device=dev)
        params['bias%d'%i] = b*sigma + mu
        params['weight%d'%i] = w*sigma + mu
        
    return params

รายการ [code: class ANN torch] แสดงโปรแกรมโครงข่ายประสาทเทียม ที่เขียนด้วยไพทอร์ช. เมื่อเปรียบเทียบโปรแกรมในรายการ [code: class ANN torch] กับโปรแกรมในรายการ [code: class ANN] จะพบว่า (1) คลาส tANN1 รับมรดก ³ มาจากคลาส ANN (รายการ [code: class ANN]) เพื่อลดความซ้ำซ้อน และ (2) เมท็อด train และ predict เพียงเปลี่ยนมาใช้คำสั่งของไพทอร์ชเท่านั้น ⁴. นอกจากนั้น เพื่อความกระชับ เมท็อด train ได้ตัด track_grad ออก (ไม่มี track_grad ในเมท็อด train เช่นในรายการ [code: class ANN torch]. หมายเหตุ track_grad ใช้ประกอบการศึกษาปัญหาการเลือนหายของเกรเดียนต์ ดูแบบฝึกหัด 1.0.0.0.2 เพิ่มเติม). ข้อควรระวังคือ เมื่อใช้ไพทอร์ช ข้อมูลเทนเซอร์ที่ประมวลผลทุกตัว ต้องอยู่ในรูปแบบเทนเซอร์ของไพทอร์ช.

ตัวอย่างคำสั่งต่อไปนี้ ฝึก และทดสอบโครงข่ายประสาทเทียมที่เขียนด้วยไพทอร์ช

[language=Python, , caption={[ตัวอย่างโปรแกรมรันโครงข่ายประสาทเทียมที่เขียนด้วยไพทอร์ช]ตัวอย่างโปรแกรมรันโครงข่ายประสาทเทียมที่เขียนด้วยไพทอร์ช}, label={code: torch ann run example}]
dev = torch.device('cpu')
net = tw_initn1([2, 8, 8, 3], dev=dev)
net['act1'] = trelu
net['act2'] = trelu
net['act3'] = tsoftmax
ann = tANN1(net, NB=50, shuffle='once')

t_losses = ann.train(x, y_onehot, tcross_entropy, 
                     lr=0.0017, epochs=500)
yp = ann.predict(ttestx)
ypn = yp.to(torch.device('cpu')).data.numpy()
yc = np.argmax(ypn, axis=0)
accuracy = np.mean(yc == testy[0,:])
print('**Test accuracy: ', accuracy)

เมื่อ x, y_onehot, และ ttestx เป็นอินพุตของข้อมูลฝึก, เอาต์พุตของข้อมูลฝึก, และอินพุตของข้อมูลทดสอบ ในรูปแบบของไพทอร์ช. ส่วน testy เป็นเอาต์พุตของข้อมุลทดสอบในรูปแบบนัมไพ.

ข้อมูลสามารถแปลงไปมาระหว่างรูปแบบของนัมไพและไพทอร์ช ได้เช่น คำสั่ง

ypn = yp.to(torch.device('cpu')).data.numpy()

แปลง yp จากรูปแบบไพทอร์ช ออกมาเป็นข้อมูลในรูปแบบนัมไพอาร์เรย์. การแปลงจากข้อมูลนัมไพอาร์เรย์ ก็สามารถแปลงเป็นไพทอร์ช ได้เช่น

x = torch.from_numpy(trainx).float().to(dev)

เป็นการแปลงข้อมูลนัมไพอาร์เรย์ trainx มาเป็นรูปแบบไพทอร์ช.

class tANN1(ANN):
    def train(self, trainX, trainY, loss, lr=0.1, epochs=1000, 
              term=1e-8, term_count_max=5):
        num_layers = self.net_params['layers']    
        last_layer = num_layers-1
        out_act = 'act%d'%last_layer    
        _, N = trainX.shape    
        A = {}
        Z = {}
        delta = {}
        dEw = {}
        dEb = {}
        train_losses = []    
        term_count = 0
        step_size = lr
        self.prepare_minibatches(N)
        for nt in range(epochs):               
            for ib in range(self.NMB):
                Z[0], batchY = self.getbatch(ib, trainX, trainY)    
                # (1) Forward pass
                for i in range(1, num_layers):
                    b = self.net_params['bias%d'%i]
                    w = self.net_params['weight%d'%i]
                    act_f = self.net_params['act%d'%i]

                    A[i] = w.mm(Z[i-1]) + b   # A: M x N
                    Z[i] = act_f(A[i])        # Z: M x N
                # end forward pass
                Yp = Z[i]
                # (2) Calculate output dE/da
                delta[last_layer] = Yp - batchY  # delta: M x N
                # (3) Backpropagate. Calc. dE/da for layer i-1
                for i in range(last_layer, 1, -1):
                    b = self.net_params['bias%d'%i]   # Mnext,1 
                    w = self.net_params['weight%d'%i] # Mnext,M
                    act_f = self.net_params['act%d'%(i-1)]

                    sumdw = w.transpose(0, 1).mm(delta[i]) # M,N
                    if act_f == trelu:
                        delta[i - 1] = tdrelu(A[i - 1]) * sumdw 
                    else:
                        assert act_f == trelu

                    # (4) Calculate gradient dE/dw and dE/db
                    dEw[i] = delta[i].mm(Z[i-1].transpose(0, 1)) 
                    dEb[i] = delta[i].mm(torch.ones(self.NB, 1, 
                        device=delta[i].device))    
                # end backpropagate

                # Calculate gradient dE/dw and dE/db
                dEw[1] = delta[1].mm(Z[0].transpose(0, 1)) 
                dEb[1] = delta[1].mm(torch.ones(self.NB, 1, 
                                device=delta[1].device))    

                # Update parameters w/ Gradient Descent
                gnorm = 0
                for i in range(1, num_layers):
                    b = self.net_params['bias%d'%i]
                    w = self.net_params['weight%d'%i]
                    b -= step_size * dEb[i]
                    w -= step_size * dEw[i]
                    
                    gnorm += torch.norm(dEb[i])
                    gnorm += torch.norm(dEw[i])                    
                # end update parameters
                
                # Calculate loss at each batch
                lossn = torch.sum(loss(Yp, batchY), dim=0) 
                train_losses.append(torch.mean(lossn))     

                # Check termination condition
                if gnorm < term:
                    term_count += 1
                    if term_count > term_count_max:
                        print('Reach term. at %d(%d)'%(nt, ib))
                        return train_losses 
                else: # reset term_count
                    term_count = 0
                # end if term_count                           
            # end ib
        # end epoch nt
        return train_losses # losses per batches 

    def predict(self, X):
        num_layers = self.net_params['layers']
        Z = X        
        for i in range(1, num_layers):            
            b = self.net_params['bias%d'%i]
            w = self.net_params['weight%d'%i]
            act_f = self.net_params['act%d'%i]
            A = w.mm(Z) + b   # A: M x N
            Z = act_f(A)      # Z: M x N
        return Z # M x N

5.0.0.1.1 แบบฝึกหัด

ศึกษาโปรแกรมในรายการ [code: class ANN torch] เปรียบเทียบกับโปรแกรมในรายการ [code: class ANN]. จงออกแบบการทดลองเพื่อทดสอบเปรียบเทียบโปรแกรมทั้งสองแบบ ทั้งในเชิงเวลาในการฝึก เวลาในการอนุมาน คุณภาพการฝึก โดยคำนึงถึงปัจจัยประกอบคือ ความลึกและความซับซ้อนของโครงข่ายประสาทเทียมที่เลือกใช้ และจำนวนจุดข้อมูลกับจำนวนมิติของอินพุต. ดำเนินการทดลอง สังเกต บันทึกผล สรุปและอภิปราย.

5.0.0.2 การคำนวณด้วยจีพียู.

จุดประสงค์หลักของการใช้ไพทอร์ช คือ การที่ไพทอร์ชสามารถส่งการคำนวณไปทำในจีพียูได้ โดยไม่ต้องยุ่งเกี่ยวกับรายละเอียดปลีกย่อยระดับล่างของการเขียนโปรแกรมขนานและการเขียนโปรแกรมจีพียู.

คำสั่ง torch.cuda.device_count() ตรวจสอบจำนวนจีพียูที่สามารถใช้งานได้. คำสั่ง dev = torch.device('cuda:0') เตรียมตัวแปรวัตถุ dev สำหรับการอ้างถึงอุปกรณ์จีพียู และเพื่อจะคำนวณด้วยจีพียู ตัวแปรเทนเซอร์ทุกตัว จะต้องกำหนดอุปกรณ์เป็นจีพียู ดังตัวอย่างเช่น x = torch.randn(D, N, device=dev, dtype=torch.float) เมื่อ D และ N เป็นจำนวนส่วนประกอบในลำดับมิติที่หนึ่งและสองตามลำดับ. หรือแม้แต่การแปลงตัวแปรจากนัมไพอาร์เรย์ ตัวอย่างเช่น torchx = torch.from_numpy(datax).float().to(dev) เมื่อ datax เป็นข้อมูลในรูปแบบนัมไพอาร์เรย์ ที่ต้องการ. สังเกตว่า นอกจากการกำหนดอุปกรณ์คำนวณแล้ว ชนิดของข้อมูลก็ถูกกำหนดเป็นเลขทศนิยมขนาดสามสิบสองบิต (32-bit floating point number).

5.0.0.2.1 แบบฝึกหัด

คล้ายกับแบบฝึกหัด 1.0.0.1.1 จงออกแบบการทดลองเพื่อทดสอบเปรียบเทียบโปรแกรมในรายการ [code: class ANN torch] เมื่อทำการคำนวณด้วยจีพียู เปรียบเทียบกับ เมื่อทำการคำนวณด้วยซีพียู ทั้งในเชิงเวลาในการฝึก เวลาในการอนุมาน คุณภาพการฝึก โดยคำนึงถึงปัจจัยประกอบคือ ความลึกและความซับซ้อนของโครงข่ายประสาทเทียมที่เลือกใช้ และจำนวนจุดข้อมูลกับจำนวนมิติของอินพุต. ดำเนินการทดลอง สังเกต บันทึกผล สรุปและอภิปราย.

หมายเหตุ ดังที่ได้อภิปราย การเปลี่ยนอุปกรณ์คำนวณ สามารถทำได้โดยการระบุอุปกรณ์ที่เทนเซอร์ทุกตัว ตัวอย่างเช่น คำสั่งในรายการ [code: torch ann run example] สามารถเปลี่ยนอุปกรณ์คำนวณเป็นจีพียู ได้โดยแก้ไขคำสั่งกำหนดอุปกรณ์ในบรรทัดที่หนึ่งเป็น dev = torch.device ('cuda') และเพิ่มคำสั่ง

x = x.to(dev)
y_onehot = y_onehot.to(dev)
ttestx = ttestx.to(dev)

เพื่อระบุอุปกรณ์ให้กับเทนเซอร์ของข้อมูลที่จะนำไปคำนวณ.

5.0.0.3 การหาเกรเดียนต์อัตโนมัติ.

นอกจากความสามารถในการเปลี่ยนอุปกรณ์การคำนวณเป็นจีพียูแล้ว ความสามารถที่สะดวกมากอย่างหนึ่งของไพทอร์ช คือ การหาค่าเกรเดียนต์ได้โดยอัตโนมัติ (ผ่านกลไกของมอดูลย่อย torch.autograd). นั่นหมายถึง เราไม่จำเป็นต้องคำนวณและเตรียมโปรแกรมเพื่อคำนวณเกรเดียนต์เอง ดังเช่น โปรแกรมที่เขียนสำหรับเมท็อด train ในรายการ [code: class ANN torch].

การหาเกรเดียนต์อัตโนมัติด้วยไพทอร์ช (1) จะต้องระบุในตัวแปรที่ต้องการคำนวณเกรเดียนต์ โดยกำหนด requires_grad ของเทนเซอร์ให้ค่าเป็น True ตัวอย่างเช่น หากต้องการคำนวณเกรเดียนต์ $\nabla_{\boldsymbol{w}} E$ ซึ่งเป็นเกรเดียนต์ของค่า $E$ ต่อตัวแปร $\boldsymbol{w}$ อาจจะระบุที่ตัวแปร $\boldsymbol{w}$ โดยตรงด้วย w.requires_grad = True หรืออาจจะระบุไปพร้อมการกำหนดค่าเริ่มต้น ด้วย

w = torch.randn(M, D, requires_grad=True)

ก็ได้. การกำหนด requires_grad เป็น True จะบอกให้ไพทอร์ชติดตามการคำนวณที่เกี่ยวข้องกับตัวแปร เพื่อนำมาคำนวณหาค่าเกรเดียนต์ได้ถูกต้อง.

จากนั้นหลังการคำนวณค่าเป้าหมาย $E$ เสร็จสิ้น (2) ต้องระบุให้ไพทอร์ชคำนวณเกรเดียนต์ ด้วยคำสั่ง เช่น E.backward() เมื่อ E เป็นตัวแปรเทนเซอร์แทนค่าเป้าหมาย $E$. ค่าเกรเดียนต์ $\nabla_{\boldsymbol{w}} E$ ที่คำนวณได้ จะเก็บไว้ที่ลักษณะประจำ (attribute) grad ของตัวแปร เช่น ในตัวอย่างนี้ คือ w.grad. แต่การปรับค่าพารามิเตอร์ ต้องทำนอกการขอบเขตของการคำนวณเกรเดียนต์อัตโนมัติ และหลังการปรับค่า ต้องล้างค่าเกรเดียนต์ออกสำหรับการคำนวณครั้งต่อไป. ตัวอย่างเช่น เมื่อต้องการปรับค่าพารามิเตอร์ อาจทำโดย

with torch.no_grad():
    w -= learning_rate * w.grad
    w.grad.zero_()

เมื่อ learning_rate เป็นค่าอัตราการเรียนรู้.

แบบฝึกหัด 1.0.0.3.1 แสดงตัวอย่างโปรแกรมโครงข่ายประสาทเทียมที่เขียนโดยใช้การหาเกรเดียนต์อัตโนมัติ และการเรียกใช้.

5.0.0.3.1 แบบฝึกหัด

รายการ [code: class ANN torch autograd] แสดงโปรแกรมโครงข่ายประสาทเทียมที่เขียนด้วยไพทอร์ชและใช้การหาเกรเดียนต์อัตโนมัติ โดยเพื่อลดความซ้ำซ้อน คลาส tANN2 รับมรดก จากคลาส tANN1 (รายการ [code: class ANN torch]).

นอกจาก คลาส tANN2 สังเกตว่า ฟังก์ชันต่างๆ ในเส้นทางของการแพร่กระจายย้อยกลับ ต้องถูกเขียนใหม่ และการเขียนเมท็อด backward ต้องเขียนการคำนวณอนุพันธ์ย้อน เช่น $\frac{\partial E}{\partial a}$ ซึ่ง $\frac{\partial E}{\partial a} = \frac{\partial z}{\partial a} \cdot \frac{\partial E}{\partial z}$ $=h'(a) \cdot \frac{\partial E}{\partial z}$. กลไกของการหาเกรเดียนต์อัตโนมัติ จะคำนวณส่วน $\frac{\partial E}{\partial z}$ มาให้. (เปรียบเทียบกับ drelu ในรายการ [code: activation functions torch] ซึ่งคำนวณ $h'(a)$. ดูสมการ $\eqref{eq: backprop delta q < L}$ ประกอบ.) ตัวอย่างนี้ แสดงฟังก์ชันเรลู และฟังก์ชันเอกลักษณ์ ฟังก์ชันอื่น ๆ ก็สามารถทำได้ในลักษณะเดียวกัน.

ดังที่ได้อภิปราย ตัวแปรที่ต้องการคำนวณเกรเดียนต์ต้องถูกระบุอย่างชัดเจน ซึ่งดำเนินการในโปรแกรม tw_initn2 (เปรียบเทียบกับ tw_initn1 จากรายการ [code: activation functions torch]).

การใช้งานสามารถทำได้ในลักษณะเดิม ตัวอย่างเช่น

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

net = tw_initn2([1, 16, 1], dev=device)
net['act1'] = auto_relu.apply
net['act2'] = auto_identity.apply

ann = tANN2(net, NB=50, shuffle='once')
train_losses = ann.train(tx, ty, sse, lr=0.2/50, epochs=500)

yp = ann.predict(torch.from_numpy(testx).float().to(device))
yn = yp.to(torch.device('cpu')).data.numpy()
print('test rmse', np.sqrt(np.mean((yn - testy)**2)))

เมื่อ tx กัย ty เป็นอินพุตและเอาต์พุตของข้อมูลฝึกในรูปแบบไพทอร์ช และ testx กับ testy เป็นอินพุตและเอาต์พุตของข้อมูลทดสอบในรูปแบบนัมไพ.

class tANN2(tANN1):
    def train(self, trainX, trainY, lossf, lr=0.1, epochs=1000,  
              term=1e-8, term_count_max=5):
        num_layers = self.net_params['layers']    
        last_layer = num_layers-1
        out_act = 'act%d'%last_layer    
        _, N = trainX.shape    
        A = {}
        Z = {}
        delta = {}
        dEw = {}
        dEb = {}
        train_losses = []    
        term_count = 0
        step_size = lr
        self.prepare_minibatches(N)

        for nt in range(epochs):               
            for ib in range(self.NMB):
                Z[0], batchY = self.getbatch(ib, trainX, trainY)    
                # (1) Forward pass
                for i in range(1, num_layers):
                    b = self.net_params['bias%d'%i]
                    w = self.net_params['weight%d'%i]
                    act_f = self.net_params['act%d'%i]
                    A[i] = w.mm(Z[i-1]) + b   # A: M x N
                    Z[i] = act_f(A[i])        # Z: M x N
                # end forward pass
                Yp = Z[i]

                # (2) Calculate loss
                loss = lossf(Yp, batchY)
                
                # (3) Calculate gradients with autograd
                loss.backward()
                
                # (4) Update parameters w/ Gradient Descent
                gnorm = 0
                for i in range(last_layer, 0, -1):
                    b = self.net_params['bias%d'%i]   # Mnext,1 
                    w = self.net_params['weight%d'%i] # Mnext,M
                    with torch.no_grad():                        
                        b -= step_size * b.grad
                        w -= step_size * w.grad
                    
                        gnorm += torch.norm(b.grad)
                        gnorm += torch.norm(w.grad)  
                        
                        b.grad.zero_()
                        w.grad.zero_()
                # end update parameters
                train_losses.append(loss.item())     

                # Check termination condition
                if gnorm < term:
                    term_count += 1                    
                    if term_count > term_count_max:
                        print('Reach term. at %d(%d)'%(nt, ib))                        
                        return train_losses # losses per batches                         
                else: # reset term_count
                    term_count = 0
                # end if term_count                                                   
            # end ib
        # end epoch nt
        return train_losses # losses per batches 

def sse(yhat, y):
    return (yhat - y).pow(2).sum()

class auto_relu(torch.autograd.Function):
    @staticmethod
    def forward(ctx, a):
        ctx.save_for_backward(a)
        return a.clamp(min=0)

    @staticmethod
    def backward(ctx, dEz):
        a, = ctx.saved_tensors
        dEa = dEz.clone()
        dEa[a < 0] = 0
        return dEa

class auto_identity(torch.autograd.Function):
    @staticmethod
    def forward(ctx, a):
        return a

    @staticmethod
    def backward(ctx, dEz):
        dEa = dEz.clone()
        return dEa

def tw_initn2(Ms, umeansigma=(0,1), dev=torch.device('cpu')):
    assert len(Ms) >= 2, 'Ms: #units, e.g., M = [2, 8, 3]'    
    num_layers = len(Ms)
    params = {'layers': num_layers}    
    mu = umeansigma[0]
    sigma = umeansigma[1]    
    for i, m in enumerate(Ms[1:], start=1):
        mprev = Ms[i-1]
        b = torch.randn((m,1), device=dev)
        w = torch.randn((m,mprev), device=dev)
        params['bias%d'%i] = b*sigma + mu
        params['weight%d'%i] = w*sigma + mu
        
        params['bias%d'%i].requires_grad = True
        params['weight%d'%i].requires_grad = True                
    return params

จากโปรแกรมตัวอย่างข้างต้น จงทดสอบโปรแกรม เปรียบเทียบกับการคำนวณเกรเดียนต์ด้วยมือ (รายการ [code: class ANN torch]) โดย ออกแบบการทดลอง เลือกหรือสร้างข้อมูล ดำเนินการทดลอง สังเกต บันทึกผล สรุปและอภิปราย. หมายเหตุ ตัวอย่างโปรแกรมในรายการ [code: class ANN torch autograd] มีฟังก์ชัน identity และ sse. ดังนั้นงานการหาค่าถดถอย สามารถทำได้ทันที แต่งานอื่นๆ เช่น การจำแนกค่าทวิภาค (ต้องการฟังก์ชันซิกมอยด์และครอสเอนโทรปีสำหรับสองค่า) หรือการจำแนกกลุ่ม (ต้องการฟังก์ชันซอฟต์แมกซ์และครอสเอนโทรปี) ซึ่งสามารถทำได้เช่นเดียวกัน แต่ต้องเตรียมฟังก์ชันที่เกี่ยวข้องให้พร้อมก่อน.

5.0.0.4 มอดูลย่อย `nn`.

การหาเกรเดียนต์อัตโนมัติ ช่วยลดภาระทั้งการวิเคราะห์เกรเดียนต์ และการเขียนโปรแกรมลงไปมาก. แม้จะลดภาระลงไปมาก แต่การโปรแกรมโครงข่ายประสาทเทียม จากปฏิบัติการพื้นฐาน (ดังเช่นที่ทำตัวอย่างในรายการ [code: class ANN torch autograd]) ถือเป็นการเขียนโปรแกรมในระดับล่าง ซึ่งเป็นภาระเชิงปัญญา (cognitive burden). เพื่อช่วยลดภาระนี้ รวมถึงช่วยในแง่ของลำดับชั้นของความคิด ⁵ (hierarchy of abstraction) การประยุกต์ใช้งานโครงข่ายประสาทเทียมลึก จะทำได้มีประสิทธิภาพกว่า เมื่อใช้มอดูลสำเร็จ เช่น มอดูล nn. มอดูล nn มีโครงสร้างและฟังก์ชันสำเร็จต่างๆ สำหรับกลไกที่มีการใช้อย่างแพร่หลาย. ตัวอย่างคำสั่ง กำหนดโครงข่ายด้วยไพทอร์ช nn แสดงในรายการ [code: class ANN torch nn] โดยตัวอย่างคำสั่ง สำหรับการฝึกและทดสอบ แสดงในรายการ [code: class ANN torch nn train test]. หมายเหตุ ในรายการ [code: class ANN torch nn train test] โปรแกรมทำ model.zero_grad() ในช่วงปลายสมัย (หลังจากทำอย่างอื่นเสร็จ) เพื่อให้เปรียบเทียบได้ตรงมาตรงไปกับการฝึกที่แสดงในรายการ [code: class ANN torch autograd]. อย่างไรก็ตาม ความนิยม คือทำการล้างค่าเกรเดียนต์ช่วงต้นสมัยฝึก (ทำก่อนที่จะทำอย่างอื่น).

device = torch.device('cuda')
Ms = [2, 8, 16, 3]
model = torch.nn.Sequential(
    torch.nn.Linear(Ms[0], Ms[1]), torch.nn.ReLU(),
    torch.nn.Linear(Ms[1], Ms[2]), torch.nn.ReLU(),
    torch.nn.Linear(Ms[2], Ms[3]),
    torch.nn.Softmax(dim = 1) ).to(device)

loss_fn = torch.nn.NLLLoss()
for t in range(nepochs):
    # (1) Forward pass
    yhat = model(tdatax.transpose(0,1))
    loss = loss_fn(torch.log(yhat), tdatay[0].long())
    # (2) Backward pass
    loss.backward()
    # (3) Update parameters
    with torch.no_grad():
        for param in model.parameters():
            param -= lr * param.grad            
    # Zero the gradients.
    model.zero_grad()

# Test the model
yp = model(ttestx.transpose(0,1))
_, yc = torch.max(yp, 1)
print('Accuracy', torch.mean((yc == ttesty[0].long()).float()))

โปรแกรมในรายการ [code: class ANN torch nn] คำนวณซอฟต์แมกซ์ด้วย torch.nn.Softmax(dim = 1) และคำนวณครอสเอนโทรปีด้วย loss = loss_fn(torch.log(yhat),tdatay[0].long()) โดย loss_fn = torch.nn.NLLLoss(). การจัดการคำนวณเช่นนี้ เพื่อให้โปรแกรมในรายการ [code: class ANN torch nn] สามารถเปรียบเทียบกับโปรแกรมที่เขียนจากปฏิบัติการพื้นฐานได้สะดวกขึ้น. แต่ในทางปฏิบัติ การคำนวณจะมีประสิทธิภาพมากกว่า หากทำโดยใช้ nn.LogSoftmax คู่กับ nn.NLLLoss หรือสะดวกกว่า โดยใช้ nn.CrossEntropyLoss ซึ่งคำนวณซอฟต์แมกซ์และครอสเอนโทรปีรวมกันเลย.

หมายเหตุ โดยดีฟอล์ต ทั้ง nn.NLLLoss และ nn.CrossEntropyLoss คำนวณค่าสูญเสียเฉลี่ยต่อของหมู่เล็กออกมา (ดีฟอล์ต เป็น reduction=’mean’. ดูรายละเอียดการทำงานของแต่ละฟังก์ชันได้จาก https://pytorch.org/docs/stable/nn.html.) ในเชิงตรรกะการทำงานแล้ว การใช้ผลรวมหรือค่าเฉลี่ย ต่างกันเพียงค่าคงที่ที่นำไปหารค่าฟังก์ชันสูญเสียเท่านั้น. แต่ในทางปฏิบัติ ความต่างนี้มีผลโดยตรง คือ (1) หากเขียนโปรแกรมเอง ผลรวม อาจทำได้อย่างมีประสิทธิภาพมาก ผ่านการจัดการคูณเมทริกซ์ แต่ค่าเฉลี่ยต้องเพิ่มการหารเข้ามา ซึ่งการหารนี้ อาจทำได้อย่างมีประสิทธิภาพมาก โดยทำที่อัตราการเรียนรู้. (2) ไม่ว่าจะเขียนโปรแกรมเอง หรือใช้โปรแกรมสำเร็จ การใช้ค่าเฉลี่ย จะให้ผลคำนวณที่ค่อนข้างคงที่ เมื่อเทียบกับจำนวนข้อมูล. นั่นคือ หากใช้ผลรวม เมื่อจำนวนข้อมูลมาก ค่าสูญเสียที่เห็น (ซึ่งคือผลรวมค่าสูญเสีย) จะมีตัวเลขใหญ่. นั่นคือ เมื่อเพิ่มจำนวนข้อมูลฝึกเข้าไป ค่าสูญเสียขณะฝึกที่เห็น จะมีค่ามากขึ้น เมื่อเปรียบเทียบกับการฝึกด้วยข้อมูลน้อย ๆ (ซึ่งไม่ได้แปลว่า การฝึกแย่ลง). แต่หากใช้ค่าเฉลี่ย ค่าสูญเสียที่เห็น (ซึ่งคือค่าสูญเสียเฉลี่ย) จะมีตัวเลขที่อยู่ในระดับเปรียบเทียบได้ ไม่ว่าจะใช้จำนวนจุดข้อมูลฝึกเท่าไร. (3) การเลือกค่าอัตราเรียนรู้ จะทำได้สะดวกกว่าในกรณีค่าเฉลี่ย. นั่นคือ หากพบค่าอัตราเรียนรู้ที่ใช้ได้ดีกับชุดข้อมูล เมื่อมีจำนวนข้อมูลน้อยๆ แล้วถ้ามีจำนวนข้อมูลเพิ่มขึ้นมามาก การใช้ค่าอัตราเรียนรู้เดิม โดยทั่วไป ก็จะสามารถใช้ได้ดี. แต่หากใช้ผลรวม เมื่อจำนวนข้อมูลเพิ่มขึ้น จะทำให้ผลรวมค่าสูญเสียและผลรวมเกรเดียนต์มากขึ้น โดยธรรมชาติ เพราะมีพจน์ที่จะรวมมากขึ้น. ดังนั้น ค่าอัตราเรียนรู้เดิม อาจจะใช้ได้ไม่ดี และอาจจะต้องปรับลดลงเป็นอัตราส่วนตามจำนวนข้อมูลที่เพิ่มขึ้น. การรู้ระลึกถึงประเด็นผลรวมหรือค่าเฉลี่ยนี้ จะช่วยให้การเลือกค่าอัตราเรียนรู้ และการอ่านผลความก้าวหน้าการฝึก ทำได้ดียิ่งขึ้น.

การใช้ nn.Sequential แม้จะสะดวก แต่หากต้องการกำหนดทอพอโลยี (topology การเชื่อมต่อ) ที่อิสระ ยืดหยุ่น และหลากหลายมากขึ้น การใช้ nn.Module (ดังแสดงในรายการ [code: class ANN torch nn.Module]) อาจจะเหมาะสมกว่า. ตัวอย่างทอพอโลยีที่เกินกว่า nn.Sequential จะสามารถบรรยายได้ มีมากมาย รวมถึง อเล็กซ์เน็ต (หัวข้อ [sec: AlexNet]).

การบันทึกแบบจำลองที่ฝึกแล้วก็สามารถทำได้ เช่น

torch.save(net.state_dict(), './sav/nn1.pth')

เมื่อ net เป็นแบบจำลองที่ต้องการบันทึกค่าเก็บไว้ และ '.sav/nn1.pth' เป็นเส้นทางและชื่อไฟล์ที่บันทึก. การเรียกใช้แบบจำลองที่บันทึกไว้สามารถทำได้ เช่น

net = Net().to(device)
net.load_state_dict(torch.load('.sav/nn1.pth'))

เมื่อ Net() เป็นโครงสร้างของแบบจำลอง. สังเกตว่า การบักทึกค่า จะบันทึกเฉพาะค่าของพารามิเตอร์ ดังนั้น การเรียกใช้แบบจำลองจึงประกอบด้วยการสร้างตัวแปรวัตถุของแบบจำลองขึ้นมาใหม่ และกำหนดค่าของพารามิเตอร์ตามค่าที่บันทึกไว้.

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = torch.nn.Linear(2, 8)
        self.fc2 = torch.nn.Linear(8, 16)
        self.fc3 = torch.nn.Linear(16, 3)

    def forward(self, x):
        z1 = torch.relu(self.fc1(x))
        z2 = torch.relu(self.fc2(z1))
        z3 = torch.nn.Softmax(dim=1)(self.fc3(z2))
        return z3

5.0.0.4.1 แบบฝึกหัด

จงทดสอบโปรแกรมโครงข่ายประสาทเทียม ที่เขียนโดยใช้มอดูล nn เปรียบเทียบกับโปรแกรมที่เขียนการคำนวณเกรเดียนต์เอง (เช่น โปรแกรมในรายการ [code: class ANN torch]) โดย ออกแบบการทดลอง เลือกหรือสร้างข้อมูล ดำเนินการทดลอง สังเกต บันทึกผล สรุปและอภิปราย.

5.0.0.5 มอดูลช่วยจัดหมู่ย่อย `utils.data.DataLoader`.

การทำการฝึกหมู่เล็ก (ดังเช่น โปรแกรมในรายการ [code: class ANN]) ก็สามารถดำเนินการได้ด้วยมอดูลย่อย utils.data.DataLoader. การใช้งาน จะต้องสร้างตัวแปรวัตถุของ DataLoader โดยการสร้างตัวแปรวัตถุนี้ ต้องกำหนดข้อมูลที่ต้องการเข้าไป และข้อมูลนี้ต้องอยู่ในรูปแม่แบบของ utils.data.Dataset ที่ตัวอย่างคำสั่งข้างล่างใช้คลาส MyDataset (รายการ [code: MyDataset]) เข้ามาช่วย.

mydat = MyDataset()
mydat.assign_data(DX, DY)
datloader = torch.utils.data.DataLoader(mydat, batch_size=50, 
                shuffle=True, num_workers=0)

เมื่อกำหนดขนาดหมู่เล็กเป็น $50$. ตัวแปร DX และ DY เป็นข้อมูลอินพุตและเอาต์พุต ชนิดไพทอร์ชเทนเซอร์ สัดส่วน $N \times D_x$ และ $N \times D_y$ ตามลำดับ โดย $N$ เป็นจำนวนจุดข้อมูล และ $D_x$ กับ $D_y$ เป็นมิติของอินพุตและเอาต์พุต.

การเรียกใช้ ก็สามารถทำได้ เช่นเดียวกับตัวแปรวนซ้ำ ⁶ อื่น ๆ ของไพธอน เช่นตัวอย่าง

for t in range(num_epochs):
    for data in trainloader:
        inputs, labels = data
        yhat = net(inputs)
        loss = loss_fn(yhat, labels[:,0])
        loss.backward()
        with torch.no_grad():
            for param in net.parameters():
                param -= learn_rate * param.grad
        net.zero_grad()

เมื่อ num_epochs และ learn_rate เป็นจำนวนสมัยฝึกและอัตราการเรียนรู้ ตามลำดับ. ในตัวอย่างคำสั่งนี้ โปรแกรม loss_fn รับเฉลยในรูปแบบไพทอร์ชเทนเซอร์ หนึ่งลำดับชั้น ⁷ ดังนัั้น คำสั่ง loss = loss_fn(yhat, labels[:,0]) จึงต้องจัดฉลากเฉลยให้อยู่ในรูปแบบดังกล่าว.

class MyDataset(torch.utils.data.Dataset):
    def __init__(self):
        super(MyDataset, self).__init__()
        self.datax = None
        self.datay = None
        
    def assign_data(self, datX, datY):
        self.datax = datX
        self.datay = datY

    def __getitem__(self, index):
        return self.datax[index,:], self.datay[index,:]
        
    def __len__(self):
        return self.datax.shape[0]

5.0.0.5.1 แบบฝึกหัด

จากแบบฝึกหัด [ex: mnist] จงเขียนโปรแกรมโดยใช้มอดูล nn และการหาเกรเดียนต์อัตโนมัติ พร้อมด้วยจัดการข้อมูลฝึกด้วย utils.data.DataLoader และเปรียบเทียบผล กับผลลัพธ์จากแบบฝึกหัด [ex: mnist] สรุป และอภิปราย.

5.0.0.5.2 แบบฝึกหัด

จากแบบฝึกหัด 1.0.0.5.1 ที่เราดาวน์โหลดข้อมูลเอง เตรียมข้อมูลเอง จัดรูปแบบต่าง ๆ จนข้อมูลสามารถนำเข้าไปใช้กับ ตัวแปรวัตถุของ DataLoader ได้. อย่างไรก็ตาม พัฒนาการของการเรียนรู้ของเครื่องและการรู้จำรูปแบบ ก้าวหน้าไปมาก และมีชุดข้อมูลที่มีการศึกษาอย่างกว้างขวาง และนิยมใช้เพื่อเรียนรู้ หรือเพื่อการทดสอบกลไกใหม่ ๆ. สำหรับชุดข้อมูลที่นิยมหลาย ๆ ชุด ไพทอร์ชมีกลไกช่่วยเหลือ ด้วยมอดูล torchvision เพื่อลดภาระในการเตรียมข้อมูลเหล่านี้ลง. ตัวอย่างคำสั่งข้างล่าง เตรียมชุดข้อมูลเอมนิสต์ตั้งแต่ดาวน์โหลด (หากยังไม่มี) ไปจนถึงจัดเข้าตัวแปรวัตถุของ DataLoader และพร้อมที่จะถูกเรียกใช้งาน

import torchvision
import torchvision.transforms as transforms

transform = transforms.Compose( [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

trainset = torchvision.datasets.MNIST(root='./data', train=True,
            download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=50,
            shuffle=True, num_workers=0)
testset = torchvision.datasets.MNIST(root='./data', train=False,
            download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=50,
            shuffle=False, num_workers=0)

เมื่อตัวแปร trainloader และ testloader คือตัวแปรวัตถุของ DataLoader สำหรับข้อมูลฝึกและข้อมูลทดสอบตามลำดับ.

จงเขียนโปรแกรม เพื่อฝึกและทดสอบชุดข้อมูลเอมนิสต์ โดยใช้ข้อมูลโหลดสำเร็จ. สังเกตผล สรุป และอภิปราย. หมายเหตุ การวัดค่าความแม่นยำของข้อมูลทดสอบที่แบ่งเป็นหมู่เล็ก จะช่วยลดภาระการใช้หน่วยความจำทีเดียวมาก ๆ ได้.

5.0.0.6 มอดูลย่อย `optim`.

ดังที่อภิปรายในหัวข้อ [sec: adv training opt] มีขั้นตอนวิธีมากมาย ที่สามารถนำมาฝึกแบบจำลองได้. มอดูล optim จัดเตรียมขั้นตอนวิธีที่นิยมต่าง ๆ ไว้ให้. โดยตัวอย่างคำสั่งต่อไปนี้ แสดงการใช้งาน วิธีลงเกรเดียนต์ ⁸ ที่ใช้อัตราเรียนรู้เป็น $0.001$ และโมเมนตัมเป็น $0.0$ โดย net คือแบบจำลองที่ต้องการฝึก

device = torch.device('cuda')
net = torch.nn.Sequential( torch.nn.Linear(784, 8), torch.nn.ReLU(),
                           torch.nn.Linear(8, 10) ).to(device)
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.001, momentum=0.0)

และการฝึกก็สามารถทำได้ดังแสดงในรายการ [code: train optim]. สังเกต โปรแกรมในรายการ [code: train optim] ล้างค่าเกรเดียนต์ net.zero_grad() ตั้งแต่ต้นของลูป.

train_losses = []
for t in range(nepochs):
    for data in trainloader:
        net.zero_grad()
        inputs, labels = data
        yhat = net(inputs)
        loss = loss_fn(yhat, labels)
        loss.backward()
        optimizer.step()
        train_losses.append(loss.item())
    # end for data
# end for t

5.0.0.6.1 แบบฝึกหัด

จงเลือกหรือสร้างข้อมูล เลือกแบบจำลอง ฝึกโดยใช้การหาค่าดีที่สุดจากมอดูล optim ทดสอบ สรุปและอภิปราย.

5.0.0.6.2 แบบฝึกหัด

จากหัวข้อ [sec: dropout] จงศึกษาและเขียนโปรแกรมสำหรับกลไกการตกออก จงเลือกหรือสร้างข้อมูล ทำแบบจำลอง โดยใช้เทคนิคการตกออกที่เขียนขึ้น ทดสอบ สังเกตผล สรุป และอภิปราย. หมายเหตุ การใช้การตกออก อาจทำให้ต้องการแบบจำลองที่ใหญ่ขึ้น(ซับซ้อนขึ้น) จากการทำแบบจำลองที่ไม่ใช้การตกออก รวมถึงอาจทำให้ต้องการจำนวนสมัยฝึกที่มากขึ้น. คำใบ้ การฝึกอาจทำได้ช้าลง แต่ให้สังเกตการลดลงของค่าฟังก์ชันสูญเสีย และในการทดสอบ อย่าลืมชดเชย การตกออก. แบบฝึกหัดนี้ ต้องการให้ได้ทดลองฝึกเขียนโปรแกรมด้วยตนเอง แต่หากต้องการ แบบฝึกหัด 1.0.0.6.3 แสดงตัวอย่างโปรแกรม.

5.0.0.6.3 แบบฝึกหัด

จงศึกษา และเปรียบเทียบโปรแกรมที่เขียนขึ้นสำหรับแบบฝึกหัด 1.0.0.6.2 กับโปรแกรมตัวอย่าง (รายการ [code: implement dropout] และการนำไปใช้ในแบบจำลอง แสดงในรายการ [code: NN with implemented dropout]. การฝึกและทดสอบ แสดงในรายการ [code: train test NN with implemented dropout]) ทั้งวิธีการเขียน และพฤติกรรมการทำงาน.

สังเกตว่า ถึงแม้ชื่อคือ การตกออก แต่ค่าความน่าจะเป็น (ตัวแปร oneprob ในรายการ [code: implement dropout] ซึ่งจะรับค่า 0.8 และ 0.5 ในรายการ [code: NN with implemented dropout]) ระบุถึง ความน่าจะเป็นของการคงอยู่. ข้อควรระวัง การใช้งานมอดูลสำเร็จ ควรศึกษาตรวจสอบพฤติกรรมการทำงานให้ชัดเจนก่อน.

class mdropout(torch.autograd.Function):
    @staticmethod
    def forward(ctx, z, onprob=0.5):
        d = torch.distributions.Bernoulli(torch.tensor([onprob]))
        mask = d.sample(sample_shape=z.shape).view(z.shape)
        mask = mask.to(z.device)
        ctx.save_for_backward(mask)     
        return mask * z

    @staticmethod
    def backward(ctx, dEzm):    
        mask, = ctx.saved_tensors
        dEz = mask * dEzm.clone()
        return dEz, None, None

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.do0 = mdropout.apply
        self.fc1 = torch.nn.Linear(784, 16)
        self.do1 = mdropout.apply
        self.fc2 = torch.nn.Linear(16, 10)

    def forward(self, x):
        z2 = None
        if self.training:
            xm = self.do0(x, 0.8, 1)
            z1 = torch.relu(self.fc1(xm))
            z1m = self.do1(z1, 0.5, 1)
            z2 = self.fc2(z1m)
        else:
            xm = 0.8 * x
            z1 = torch.relu(self.fc1(xm))
            z1m = 0.5 * z1
            z2 = self.fc2(z1m)                
        return z2

loss_fn = torch.nn.CrossEntropyLoss()
device = torch.device('cuda')   
net = Net().to(device)
net.train() # Set mode to 'train' (net.Training = True)
optimizer = torch.optim.SGD(net.parameters(), lr=1e-4)
nepochs = 50
train_losses = []
for t in range(nepochs):
    for i, data in enumerate(trainloader):
        net.zero_grad()	
        inputs, labels = data
        yhat = net(inputs)
        loss = loss_fn(yhat, labels)
        loss.backward()
        optimizer.step()
        train_losses.append(loss.item())
    # end for data
# end for t

# Test
net.eval() # Set mode to 'eval' (net.Training = False)
correct = 0
num = 0
for data in testloader:
    inputs, labels = data
    yp = net(inputs)
    _, yc = torch.max(yp, 1)
    correct += torch.sum((yc == labels).float())
    num += len(y)    
print('Accuracy', correct/num)

5.0.0.6.4 แบบฝึกหัด

ดังที่อภิปรายในหัวข้อ [sec: dropout] การตกออก อาจดำเนินการชดเชย โดยใช้การหารค่าความน่าจะเป็น ออกจากค่าหน่วยย่อย ตอนฝึก แทนการคูณเข้า ขณะทำการอนุมาน. ตัวอย่างโปรแกรมในรายการ [code: implement dropout multiply w] แสดงโปรแกรมการตกออก ที่เขียนโดยใช้การหาร ตอนฝึก เพื่อชดเชยค่าที่ตกออกไป. จงเปรียบเทียบความต่างกับโปรแกรมในรายการ [code: implement dropout] ทั้งวิธีการเขียน และพฤติกรรมการทำงาน.

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.do0 = mdropout.apply
        self.fc1 = torch.nn.Linear(784, 16)
        self.do1 = mdropout.apply
        self.fc2 = torch.nn.Linear(16, 10)

    def forward(self, x):
        z2 = None
        if self.training:
            xm = self.do0(x, 0.8, 1) / 0.8
            z1 = torch.relu(self.fc1(xm))
            z1m = self.do1(z1, 0.5, 1) / 0.5
            z2 = self.fc2(z1m)
        else:
            xm = x
            z1 = torch.relu(self.fc1(xm))
            z1m = z1
            z2 = self.fc2(z1m)                
        return z2

5.0.0.7 การตกออก ด้วย `nn.Dropout`.

มอดูล nn มีมอดูลย่อยสำหรับทำการตกออก คือ nn.Dropout. ตัวอย่างคำสั่งข้างล่าง แสดงการใช้ nn.Dropout เพื่อใช้งานกลไกการตกออก ในลักษณะเดียวกับโปรแกรมในรายการ [code: NN with implemented dropout].

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.do0 = torch.nn.Dropout(p=0.2)
        self.fc1 = torch.nn.Linear(784, 16)
        self.do1 = torch.nn.Dropout(p=0.5)
        self.fc2 = torch.nn.Linear(16, 10)

    def forward(self, x):
        xm = self.do0(x)
        z1 = torch.relu(self.fc1(xm))
        z1m = self.do1(z1)
        z2 = self.fc2(z1m)
        return z2

สังเกตการใช้ nn.Dropout ไม่ต้องกำหนดการคำนวณแยกระหว่างการฝึก และการอนุมาน (เช่นที่ต้องทำในรายการ [code: NN with implemented dropout]) เพราะว่า nn.Dropout มีกลไกภายในที่จัดการเรื่องนี้ให้.

นอกจากนั้น nn.Dropout รับความน่าจะเป็นที่จะตกออก (เปรียบเทียบกับ โปรแกรมในรายการ [code: implement dropout] ที่เป็นความน่าจะเป็นของการคงอยู่) ดังนั้น ณ ที่นี้ self.do0 สำหรับอินพุตจึงใช้ p=0.2 ซึ่งคือ โอกาสตกออกเป็น $0.2$ (หรือโอกาสคงอยู่ $0.8$).

5.0.0.7.1 แบบฝึกหัด

จากแบบฝึกหัด 1.0.0.6.2 จงทำแบบจำลองที่ใช้กลไกการตกออก โดยใช้ nn.Dropout เปรียบเทียบโปรแกรม การทำงาน และผลการทำงาน สรุปผล และอภิปราย.

5.0.0.7.2 แบบฝึกหัด

จงศึกษาการทำงานและผลของการใช้การตกออก โดยเปรียบเทียบกับ (1) การไม่ใช้เทคนิคการตกออก และ (2) การทำค่าน้ำหนักเสื่อม. ทดสอบกับข้อมูลที่มีความยากต่าง ๆ กัน มีปริมาณข้อมูลต่าง ๆ กัน และเมื่อแบบจำลองมีความซับซ้อนต่าง ๆ กัน. สังเกตผล สรุปและอภิปราย.

5.0.0.7.3 แบบฝึกหัด

จงเขียนโปรแกรมโครงข่ายประสาทเทียม ที่มีชั้นสัญญาณรบกวน ที่รับค่าหน่วยย่อย $\boldsymbol{z}$ เป็นอินพุต และให้ค่า $\boldsymbol{z}'$ เป็นเอาต์พุต โดย $\boldsymbol{z}' = \boldsymbol{m} \odot \boldsymbol{z}$ เมื่อ $\boldsymbol{m}$ เป็นเมทริกซ์ขนาดเดียวกับ $\boldsymbol{z}$ และแต่ละส่วนประกอบ $m \sim \mathcal{N}(1, \sigma)$ และ $\sigma$ เป็นอภิมานพารามิเตอร์ กำหนดจากผู้ใช้.

ออกแบบการทดลอง เพื่อทดสอบประสิทธิภาพการใช้ชั้นสัญญาณรบกวน เปรียบเทียบกับการตกออก ทั้งเรื่องการฝึก และผลของแบบจำลองที่ฝึกได้. ดำเนินการทดลอง สังเกตผล สรุปและอภิปราย. ศึกษางานวิจัยของศรีวาสทาวาและคณะ อภิปรายผลที่ได้ เปรียบเทียบกับผลจากศรีวาสทาวาและคณะ.

รายการ [code: implement noise multiply w] แสดงตัวอย่างโปรแกรม. สังเกตว่า การใช้ชั้นสัญญาณรบกวน สะดวกกว่าการตกออก ในแง่ที่ไม่ต้องทำการชดเชยขณะใช้งานอนุมาน.

class mnoise(torch.autograd.Function):
    @staticmethod
    def forward(ctx, z, sigma=1):
        d =torch.distributions.normal.Normal(torch.tensor([1.0]), 
                                           torch.tensor([sigma]))
        mask = d.sample(sample_shape=z.shape).view(z.shape)
        mask = mask.to(z.device)
        ctx.save_for_backward(mask)     
        return mask * z

    @staticmethod
    def backward(ctx, dEzm):    
        mask, = ctx.saved_tensors
        dEz = mask * dEzm.clone()
        return dEz, None, None

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.do0 = mnoise.apply
        self.fc1 = torch.nn.Linear(784, 16)
        self.do1 = mnoise.apply
        self.fc2 = torch.nn.Linear(16, 10)

    def forward(self, x):
        z2 = None
        if self.training:
            xm = self.do0(x, 1.0)
            z1 = torch.nn.ReLU()(self.fc1(xm))
            z1m = self.do1(z1, 1.0)
            z2 = self.fc2(z1m)
        else:
            xm = x
            z1 = torch.nn.ReLU()(self.fc1(xm))
            z1m = z1
            z2 = self.fc2(z1m)
                
        return z2

5.0.0.7.4 แบบฝึกหัด

การทำนายการแจกแจง. แม้การหาค่าถดถอย การจำแนกค่าทวิภาค และการจำแนกกลุ่ม เป็นกลุ่มภาระกิจที่มีการใช้งานมากที่สุด แต่การใช้งานโครงข่ายประสาทเทียม ไม่ได้จำกัดอยู่แต่เฉพาะกลุ่มภาระกิจที่นิยมเหล่านี้. โครงข่ายประสาทเทียม สามารถประยุกต์ใช้งานได้กว้างขวาง ⁹ . หลักการของวิธีค่าฟังก์ชันควรจะเป็นสูงสุด (maximum likelihood) เป็นแนวทางหนึ่งที่ทั่วไปมากพอ ที่สามารถใช้ออกแบบฟังก์ชันจุดประสงค์สำหรับภาระกิจต่าง ๆ ที่ต้องการได้.

หลักการของวิธีค่าฟังก์ชันควรจะเป็นสูงสุด คือ หากกำหนดให้ $\boldsymbol{X}$ และ $\boldsymbol{Y}$ เป็นข้อมูลที่สนใจ และ $p(\boldsymbol{Y}|\boldsymbol{X}; \boldsymbol{\theta})$ เป็น ค่าประมาณความน่าจะเป็น โดย $\boldsymbol{\theta}$ เป็นพารามิเตอร์แล้ว ค่าของพารามิเตอร์ $\boldsymbol{\theta}$ สามารถหาได้จาก \[\begin{eqnarray} \boldsymbol{\theta}^\ast &=& \arg\max_{\boldsymbol{\theta}} p(\boldsymbol{Y}|\boldsymbol{X}; \boldsymbol{\theta}) \label{eq: maximum likelihood} \end{eqnarray}\] เมื่อ $\boldsymbol{\theta}^\ast$ คือค่าพารามิเตอร์ที่ดีที่สุด (สำหรับแบบจำลองและข้อมูลที่มี).

แบบฝึกหัดนี้ เราจะศึกษาการทำโครงข่ายประสาทเทียมสำหรับทำนายการแจกแจงของข้อมูล. นั่นคือ จากที่เคยใช้โครงข่ายประสาทเทียม $f$ ทำนายค่าเอาต์พุต $y$ จากอินพุต $x$ แบบฝึกหัดนี้จะใช้โครงข่ายประสาทเทียมทำนายการแจกแจงของเอาต์พุต $y$ จากอินพุต $x$. แนวทางคือ แทนที่จะใช้โครงข่ายประสาทเทียมทำนายค่าความน่าจะเป็น ¹⁰ $p(y|x)$ โดยตรง เราจะใช้โครงข่ายประสาทเทียมทำนาย $\boldsymbol{\theta}(x)$ ซึ่งนำไปใช้คำนวณค่าประมาณความน่าจะเป็น $p(y; \boldsymbol{\theta}(x)) \approx p(y|x)$ อีกต่อหนึ่ง.

แบบฝึกหัดนี้ การประมาณความน่าจะเป็น $p(y; \boldsymbol{\theta}(x))$ จะคำนวณด้วย แบบจำลองความหนาแน่นผสม (mixture density model). แบบจำลองความหนาแน่นผสม เป็นแบบจำลองทั่วไปในการประมาณค่าเอาต์พุต จากอินพุต โดยรวมค่าประมาณจากส่วนผสมต่าง ๆ เข้าด้วยกัน อาจมองว่า แบบจำลองความหนาแน่นผสม มีพื้นฐานจากกฎผลบวก และกฎผลคูณของทฤษฎีเบส์ได้ อันคือ $p(y|x) = \sum_{i=1}^M p(y|c=i) p(c=i|x)$ เมื่อ $c=i$ แทนส่วนผสม $i$ และ $M$ คือจำนวนส่วนผสมทั้งหมด. ส่วนผสม $c=i$ อาจมองเสมือนว่าเป็นสถานะภายในของความสัมพันธ์ระหว่าง $x$ กับ $y$ ก็ได้. ค่า $p(y|c=i)$ ถูกประมาณด้วยความหนาแน่นของการแจกแจงเกาส์เซียน. ดังนั้น สรุปคือ แบบจำลองความหนาแน่นผสม คำนวณ \[\begin{eqnarray} p(y; \boldsymbol{\theta}(x)) = \sum_{i=1}^M p(c=i|x) \cdot \mathcal{N}(y; \mu_i(x), \sigma_i(x)) \label{eq: GMM p(y; theta(x))} \end{eqnarray}\] เมื่อ $p(c=i|x)$ แทนความน่าจะเป็นของส่วนผสม $i$ และ $\mathcal{N}(y; \mu_i(x), \sigma_i(x))$ เป็นค่าความหนาแน่นความน่าจะเป็นของการแจกแจงเกาส์เซียน ที่มีค่าเฉลี่ย $\mu_i(x)$ กับค่าเบี่ยงเบนมาตราฐาน $\sigma_i(x)$. แบบจำลองเกาส์เซียนผสม สามารถใช้ประมาณค่าความน่าจะเป็นจากการแจกแจงใด ๆ ได้ หากมีจำนวนส่วนผสมเพียงพอ. จำนวนส่วนผสม $M$ เป็นอภิมานพารามิเตอร์ของแบบจำลอง.

สังเกต รูปแบบสมการ $\eqref{eq: GMM p(y; theta(x))}$ เขียนสำหรับกรณีเอาต์พุตมิติเดียว ($y \in \mathbb{R}$). กรณีทั่วไป ก็สามารถคำนวณได้ในลักษณะเดียวกัน นั่นคือ $p(\boldsymbol{y}; \boldsymbol{\theta}(\boldsymbol{x})) = \sum_{i=1}^M p(c=i|\boldsymbol{x}) \cdot \mathcal{N}(\boldsymbol{y}; \boldsymbol{\mu}_i(\boldsymbol{x}), \boldsymbol{\Sigma}_i(\boldsymbol{x}))$.

สำหรับจุดข้อมูลที่ $n^{th}$ ค่าความน่าจะเป็น $p(y_n|x_n) \approx p(y_n; \boldsymbol{\theta}(x_n))$ และด้วยสมมติฐานไอ.ไอ.ดี. (i.i.d. ย่อจาก independent and identically distributed random variables ซึ่ง ณ ที่นี้ หมายถึง สมมติฐานว่าจุดข้อมูลแต่ละจุดเป็นอิสระต่อกัน และมีการแจกแจงเหมือนกัน) จะได้ว่า \[p([y_1, y_2, \ldots, y_N]|[x_1, x_2, \ldots, x_N]) = \prod_{n=1}^N p(y_n|x_n)\] เพื่อความสะดวกในการคำนวณ ค่าลอการิทึมของฟังก์ชันควรจะเป็น (log likelihood) จะถูกนิยมมากกว่า. นอกจากนั้น สำหรับการฝึกแบบจำลอง นิยมวางกรอบเป็นปัญหาค่าน้อยที่สุด ค่าฟังก์ชันสูญเสีย สามารถกำหนดเป็น ค่าลบลอการิทึมของฟังก์ชันควรจะเป็น (negative log likelihood). ดังนั้น ค่าฟังก์ชันสูญเสีย สามารถนิยามได้เป็น \[\begin{eqnarray} \mathrm{loss} &=& -\log \prod_{n=1}^N p(y_n|x_n) \nonumber \\ &=& -\sum_n \log p(y_n|x_n) \label{eq: neg log likelihood} \\ &=& -\sum_n \log \sum_{i=1}^M p(c=i|x_n) \cdot \mathcal{N}(y_n; \mu_i(x_n), \sigma_i(x_n)) \label{eq: neg log likelihood GMM} \end{eqnarray}\]

สมการ $\eqref{eq: neg log likelihood GMM}$ ได้จากการใช้แบบจำลองความหนาแน่นผสม. โครงข่ายประสาทเทียม สามารถใช้เพื่อประมาณ พารามิเตอร์ของแบบจำลองความหนาแน่นผสม $\boldsymbol{\theta} = [p(c=i|x), \mu_i(x), \sigma_i(x)]^T$ สำหรับ $i=1, \ldots, M$.

จงศึกษาการทำโครงข่ายประสาทเทียม สำหรับประมาณการแจกแจง ซึ่งมีรายละเอียด คือ (1) จงสร้างข้อมูล $\{x_n,y_n\}$ สำหรับ $n=1, \ldots, N$ โดยกำหนดความสัมพันธ์ระหว่างตัวแปรต้น $x_n$ และตัวแปรตาม $y_n$ ดังนี้
(a) สำหรับแต่ละค่าของตัวแปรต้น $x$ ตัวแปรตาม $y$ แสดงออกได้สองลักษณะ.
(b) ลักษณะแรก $y \sim \mathcal{N}(\mu_0(x), \sigma_0(x))$
โดย $\mu_0(x) = 0.05 x^2 + 4$ และ $\sigma_0(x) = 0.2 + \log\left(1 + \exp(x-5)\right)$.
(c) ลักษณะที่สอง $y \sim \mathcal{N}(\mu_1(x), 0.5)$ โดย $\mu_1(x) = -0.05 x^2 - 4$.
(d) โอกาสที่ $y$ จะแสดงออกในลักษณะแรก เป็น $0.25+ \frac{0.5}{1 + \exp(-0.4 x)} \times 100\%$. นอกนั้น $y$ จะแสดงออกในลักษณะที่สอง.
(2) จงกำหนดโครงข่ายประสาทเทียม ฝึก ทดสอบ สังเกตผล สรุป และอภิปราย.

จากข้อกำหนดของข้อมูล สังเกตว่า (ก) ลักษณะข้อมูลเป็นไปตามแบบจำลองความหนาแน่นผสม และจำนวนลักษณะแสดงออก คือจำนวนส่วนผสม นั่นคือ $M = 2$. (ข) ความน่าจะเป็นของลักษณะแรก $p_0 = p(c=0|x) = 0.25+ \frac{0.5}{1 + \exp(-0.4 x)}$ และความน่าจะเป็นของลักษณะที่สอง $p_1 = p(c=1|x) = 1 - p(c=0|x)$. ทั้ง $p_0$ และ $p_1$ เป็นฟังก์ชันของ $x$. (ค) ลักษณะแรก ทั้งค่าเฉลี่ย $\mu_0$ และค่าเบี่ยงเบนมาตราฐาน $\sigma_0$ เป็นฟังก์ชันของ $x$. ส่วนลักษณะที่สอง ค่าเฉลี่ย $\mu_1$ เป็นฟังก์ชันของ $x$ แต่ค่าเบี่ยงเบนมาตราฐาน $\sigma_1$ เป็นค่าคงที่. (ง) ตัวแปรต้น $x \in \mathbb{R}$ ดังนั้น โครงข่ายประสาทเทียมรับอินพุตหนึ่งมิติ. (จ) พารามิเตอร์ของแบบจำลองความหนาแน่นผสม จะมีทั้งหมด $6$ ตัว ได้แก่ $\boldsymbol{\theta} = [p_0, p_1, \mu_0, \mu_1, \sigma_0, \sigma_1]^T$ ซึ่งทั้ง $6$ ค่านี้ จะคำนวณมาจากโครงข่ายประสาทเทียม. ดังนั้น โครงข่ายประสาทเทียมให้เอาต์พุตหกมิติ. สรุปคือ โครงข่ายประสาทเทียม $f: \mathbb{R} \mapsto \mathbb{R}^6$.

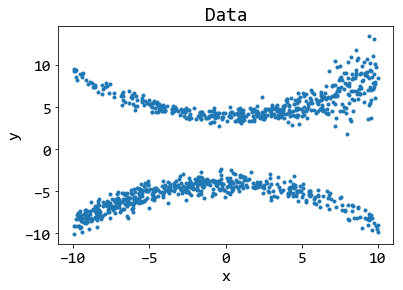
รูป 5 แสดงตัวอย่างจุดข้อมูลที่สร้างตามข้อกำหนด. สังเกตว่า ที่ตัวแปรต้น $x$ แต่ละค่า ตัวแปรตาม จะแสดงออกเป็นสองลักษณะ ซึ่งทั้งสองลักษณะมีการแจกแจงแบบสุ่ม โดยลักษณะแรก มีค่ามากกว่าลักษณะที่สอง และแนวโน้มข้อมูลจะโค้งขึ้น ในขณะที่ลักษณะที่สอง แนวโน้มข้อมูลจะโค้งลง. (เกี่ยวข้องกับ $\mu_0$ และ $\mu_1$.) จุดข้อมูลลักษณะแรก จะเบาบาง (มีสัดส่วนจำนวนจุดน้อยกว่า) จุดข้อมูลลักษณะที่สอง ในช่วงค่า $x < 0$. จุดข้อมูลลักษณะที่สอง ดูเบาบางลง เมื่อ $x > 0$. (เกี่ยวข้องกับ $p_0$ และ $p_1$.) การแจกแจงของจุดข้อมูลลักษณะที่สอง ดูคงที่ตลอดช่วงค่าของ $x$ แต่จุดข้อมูลลักษณะแรก ดูเหมือนมีการแจกแจงเพิ่มขึ้นอย่างเห็นได้ชัดในช่วง $x$ มีค่ามาก ๆ. (เกี่ยวข้องกับ $\sigma_0$ และ $\sigma_1$.)

ตัวอย่างจุดข้อมูล สำหรับโครงข่ายประสาทเทียม เพื่อทำนายการแจกแจง. แกนนอน แสดงค่าตัวแปรต้น x และแกนตั้ง แสดงค่าตัวแปรตาม y. — ตัวอย่างจุดข้อมูล สำหรับโครงข่ายประสาทเทียม เพื่อทำนายการแจกแจง. แกนนอน แสดงค่าตัวแปรต้น $x$ และแกนตั้ง แสดงค่าตัวแปรตาม $y$.

ตัวอย่างโปรแกรม สำหรับสร้างข้อมูล แสดงในรายการ [code: dist learn relation]. โปรแกรมเขียนเป็นคลาส และเมท็อดที่ใช้สร้างข้อมูล คือ sim_y ซึ่งจะสร้างข้อมูลตัวแปรตาม ขึ้นมาจากข้อมูลตัวแปรต้นที่รับเข้าไป. โปรแกรม สามารถทดสอบได้ง่ายๆ ด้วยคำสั่ง

r = relation()
xs = np.linspace(-10, 10, 1000)
ys = r.sim_y(xs)

ซึ่งค่า xs และ ys สามารถนำไปวาดกราฟ เพื่อดูความสัมพันธ์ได้.

class relation:
    def __init__(self):
        self.num_modes = 2
        self.mode_chances =[lambda x:0.25+0.5/(1+np.exp(-0.4*x)), 
                    lambda x: 1-(0.25+0.5/(1 + np.exp(-0.4*x)))]
        self.fmu_y = [lambda x: 0.05*x**2 + 4, 
                      lambda x: -0.05*x**2 - 4]
        self.fsigma_y = [lambda x: 0.2 + np.log(1 + np.exp(x-5)),
                         lambda x: 0.5*np.ones(x.shape)]

    def sim_y(self, xs):
        N = len(xs)
        p = np.random.uniform(0,1,N)
        ys = np.array([])
        for n in range(N):
            xn = xs[n]
            mode = self.num_modes-1
            for i in range(self.num_modes-1):
                pi = self.mode_chances[i](xn)            
                p[n] -= pi
                if p[n] < 0:
                    mode = i
                    break
            mun = self.fmu_y[mode](xn).reshape((-1,))
            D = mun.shape[0]
            sigman = self.fsigma_y[mode](xn).reshape((D,D))            
            yn = np.random.multivariate_normal(\
                            mun,sigman,1).item()
            ys = np.r_[ys, yn]
        return ys

ตัวอย่างโปรแกรมคำนวณฟังก์ชันสูญเสีย (คำนวณสมการ $\eqref{eq: neg log likelihood GMM}$) แสดงในรายการ [code: dist learn loss]. สังเกต (1) แบบจำลองความหนาแน่นผสม ถูกโปรแกรมเป็นส่วนหนึ่งของฟังก์ชันสูญเสีย. (2) ค่าความหนาแน่น $\mathcal{N}(\mu, \sigma) = \frac{1}{\sigma \sqrt{2 \pi}} \exp \left( -0.5 \left(\frac{y - \mu}{\sigma}\right)^2 \right)$ คำนวณโดยปฏิบัติการพื้นฐาน ไม่ได้ใช้ฟังก์ชันสำเร็จ.

def loss1(dhat, Y):
    dmode, dmu, dsigma = dhat
    eps = 1e-45
    likelihood = dmode*torch.exp(\
        -0.5*((Y.view(-1,1) - dmu)/dsigma)**2) 
    likelihood /= dsigma*torch.sqrt(\
        torch.Tensor([2.0*np.pi])).to(Y.device)
    loglikelihood = torch.log(likelihood.sum(dim=1) + eps).sum()
    NLL = -loglikelihood
    return NLL

ค่าเอาต์พุตของโครงข่าย $\hat{y} = [p_0, p_1, \mu_0, \mu_1, \sigma_0, \sigma_1]^T$ มีลักษณะต่าง ๆ กัน. ค่า $p_0$ และ $p_1$ เป็นค่าความน่าจะเป็น ซึ่ง $p_i \in [0,1]$ และ $\sum_i p_i = 1$. ดังนั้น โปรแกรมตัวอย่าง (รายการ [code: dist ann]) ใช้ฟังก์ชันซอฟต์แมกซ์ ¹¹ สำหรับ $[p_0, p_1]^T$ เพื่อคุมเงื่อนไขนี้. ค่า $\mu_0$ และ $\mu_1$ ไม่มีข้อจำกัดอะไร. ค่า $\sigma_0$ และ $\sigma_1$ เป็นค่าเบี่ยงเบนมาตราฐาน ซึ่ง $\sigma_i > 0$. โปรแกรมตัวอย่าง ใช้ฟังก์ชันบวกอ่อน $h(a) = \log(1 + \exp(a))$ สำหรับ $[\sigma_0, \sigma_1]^T$ เพื่อคุมเงื่อนไขนี้.

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(1, 8)
        self.fc2 = nn.Linear(8, 6) 

    def forward(self, x):
        z1 = nn.ReLU()(self.fc1(x))
        z2 = self.fc2(z1)
        ymode = nn.Softmax(dim=1)(z2[:,:2])
        ymu = z2[:, 2:4]
        ysigma = nn.Softplus()(z2[:, 4:])                
        return ymode, ymu, ysigma

ด้วยข้อมูล (รายการ [code: dist learn relation]), แบบจำลอง (รายการ [code: dist ann]), และฟังก์ชันสูญเสีย (รายการ [code: dist learn loss]) การฝึกก็สามารถทำได้ในลักษณะเดียวกับภาระกิจอื่น ๆ. อย่างไรก็ตาม รายการ [code: dist ann train] แสดงโปรแกรม train สำหรับตัวอย่างการฝึกโครงข่ายเพื่อทำนายการแจกแจง. การฝึกสามารถทำได้ เช่นตัวอย่างคำสั่ง

device = torch.device('cuda')
net = Net().to(device)
net, train_losses = train(net, device, 500, 0.001)

สำหรับการรันด้วยจีพียู $500$ สมัยฝึก ด้วยค่าอัตราเรียนรู้เป็น $0.001$.

หมายเหตุ การทำแบบฝึกหัดนี้ ไม่จำเพาะต้องใช้โครงสร้างแบบจำลองตามตัวอย่าง หรือไม่จำเป็นต้องฝึกดังโปรแกรม train ไม่จำเป็นต้องใช้ขั้นตอนวิธีอดัม หรือไม่จำเป็นต้องสร้างข้อมูลใหม่ทุกสมัยฝึก สามารถเลือกวิธีทำ และดำเนินการได้อย่างอิสระ.

def train(net, device, nepochs, lr):
    r = relation()
    optimizer = torch.optim.Adam(net.parameters(), lr=lr)
    net.train()
    train_losses = []
    for t in range(nepochs):
        optimizer.zero_grad()
        x, y = getdata(device, r)
        yhat = net(x)
        loss = loss1(yhat, y)
        loss.backward()        
        optimizer.step()
        train_losses.append(loss.item())
        if t % 50 == 49:
            print('* loss', loss.item())            
        if torch.isnan(loss).item() > 0:
            print('NaN break!')
            break        
    # end for t
    return net, train_losses

def getdata(dev, process):    
    xs = np.random.uniform(-10, 10, 1000)
    ys = process.sim_y(xs)
    txs = torch.from_numpy(xs).float().to(dev)
    tys = torch.from_numpy(ys).float().to(dev)
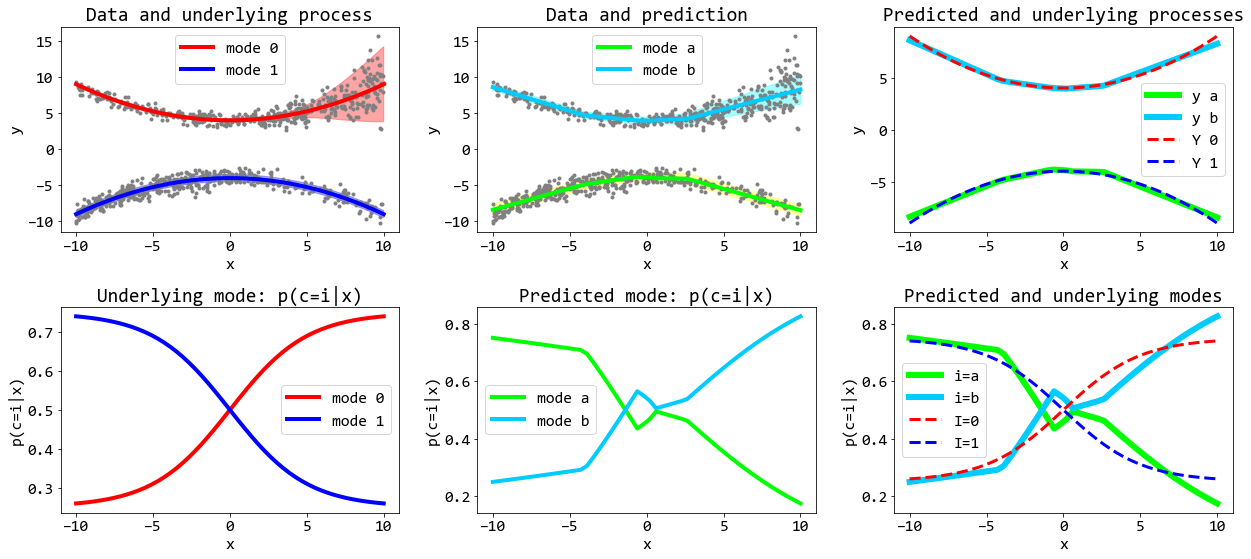
    return txs.view(-1,1), tys

รูป 6 แสดงตัวอย่างผลลัพธ์ ¹² จากการฝึกแบบจำลองดังตัวอย่าง. เนื่องจากลำดับของลักษณะไม่ได้สำคัญ ดังนั้น เพื่อลดความสับสนจากลำดับ ค่าเฉลยที่ใช้สร้างข้อมูลจะติดฉลากเป็น mode 0 และ mode 1 ในขณะที่ ผลทำนายจากแบบจำลอง จะติดฉลากเป็น mode a และ mode b.

จากการเปรียบเทียบ จะเห็นว่า แบบจำลองทำนายค่าเฉลี่ย $\mu_0$ และ $\mu_1$ ได้ดีมาก เปรียบเทียบ ภาพบนซ้ายกับภาพบนกลาง จะเห็นแนวเส้นคล้ายกันมาก (เส้นทึบฟ้า mode b คล้ายเส้นทึบแดง mode 0 และ เส้นทึบเขียว mode a คล้ายเส้นทึบน้ำเงิน mode 1) ความน่าจะเป็นของส่วนผสม แบบจำลองก็ทำนายได้ดีพอสมควร เปรียบเทียบภาพล่างซ้ายและภาพล่างกลาง.

ภาพขวาบนและล่าง แสดงค่าเฉลี่ย (ภาพบน) และความน่าจะเป็นของส่วนผสม (ภาพล่าง) ทั้งของเฉลยและที่ทำนายในภาพเดียวกัน. ค่าเบี่ยงเบนมาตราฐาน แสดงด้วยความหนาของพื้นที่แรงเงา ในภาพบนซ้าย (เฉลย) และภาพบนกลาง (ค่าทำนาย) ซึ่ง ลักษณะที่สอง (mode 1 ภาพซ้าย และ mode a ภาพกลาง) อาจจะมองเห็นความหนาได้ยาก แต่ลักษณะแรก โดยเฉพาะช่วงปลาย เห็นชัดเจนว่า เฉลยมีค่าเบี่ยงเบนมาตราฐานที่หนามาก แต่ค่าที่ทำนาย แม้จะดูหนาขึ้นในช่วงปลาย แต่ก็ดูแคบกว่าเฉลยมาก.

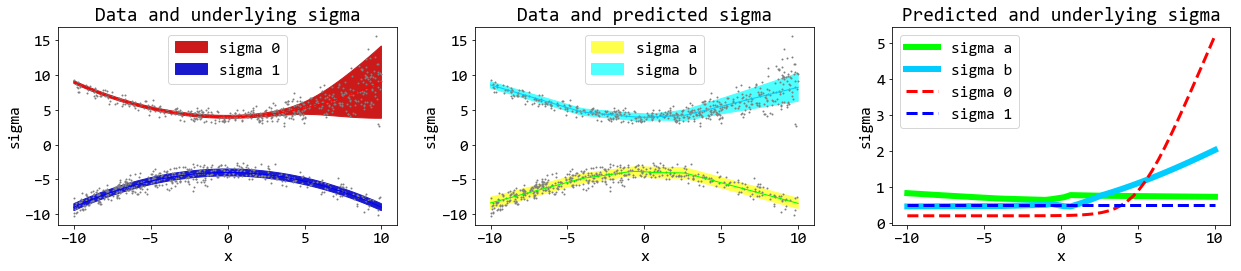
รูป 7 เน้นแสดงผลจากค่าเบี่ยงเบนมาตราฐาน (จุดข้อมูลแสดงด้วยขนาดที่เล็กลง และสีพื้นทีแรเงา เลือกให้เข้มขึ้น ในภาพซ้ายและภาพกลาง). ภาพขวา แสดงค่าเบี่ยงเบนมาตราฐาน ของทั้งเฉลยและทำนายในภาพเดียวกัน. ถึงแม้ค่าที่ทำนายอาจจะยังดูห่างจากเฉลยมาก แต่เห็นได้ชัดว่าแบบจำลองสามารถจับแนวโน้มของ $\sigma_0$ (sigma b) ที่เพิ่มในช่วงปลาย และ $\sigma_1$ (sigma a) ที่คงที่ตลอดช่วงได้.

ผลลัพธ์การเรียนการแจกแจง. ภาพบนซ้ายและกลาง แสดงจุดข้อมูล (จุดสีเทา) พร้อมค่าเฉลี่ย (\mu_0 เส้นสีแดง กับ \mu_1 สีน้ำเงินในภาพซ้าย และเส้นฟ้ากับสีเขียวในภาพกลาง) และค่าเบี่ยงเบนมาตราฐาน (\sigma_0 และ \sigma_1) ซึ่งแสดงด้วยความกว้างของพื้นที่แรเงา. ภาพบนขวา แสดงค่าเฉลี่ยของทั้งค่าที่ทำนาย (ใช้สัญลักษณ์ y a และ y b สำหรับ mode a และ mode b ตามลำดับ) และค่าเฉลย (ใช้สัญลักษณ์ Y 0 และ Y 1 สำหรับ mode 0 และ mode 1 ตามลำดับ). ภาพล่างซ้ายและกลาง แสดงค่าความน่าจะเป็นของส่วนผสม (p_0 เส้นสีแดง กับ p_1 เส้นสีน้ำเงิน ในภาพซ้าย และเส้นสีฟ้ากับเส้นสีเขียวในภาพกลาง). ภาพล่างขวา แสดงค่าความน่าจะเป็นของส่วนผสมทั้งค่าที่ทำนาย (ใช้สัญลักษณ์ i=a และ i=b สำหรับ mode a และ mode b ตามลำดับ) และค่าเฉลย (ใช้สัญลักษณ์ I=0 และ I=1 สำหรับ mode 0 และ mode 1 ตามลำดับ). — ผลลัพธ์การเรียนการแจกแจง. ภาพบนซ้ายและกลาง แสดงจุดข้อมูล (จุดสีเทา) พร้อมค่าเฉลี่ย ($\mu_0$ เส้นสีแดง กับ $\mu_1$ สีน้ำเงินในภาพซ้าย และเส้นฟ้ากับสีเขียวในภาพกลาง) และค่าเบี่ยงเบนมาตราฐาน ($\sigma_0$ และ $\sigma_1$) ซึ่งแสดงด้วยความกว้างของพื้นที่แรเงา. ภาพบนขวา แสดงค่าเฉลี่ยของทั้งค่าที่ทำนาย (ใช้สัญลักษณ์ `y a` และ `y b` สำหรับ `mode a` และ `mode b` ตามลำดับ) และค่าเฉลย (ใช้สัญลักษณ์ `Y 0` และ `Y 1` สำหรับ `mode 0` และ `mode 1` ตามลำดับ). ภาพล่างซ้ายและกลาง แสดงค่าความน่าจะเป็นของส่วนผสม ($p_0$ เส้นสีแดง กับ $p_1$ เส้นสีน้ำเงิน ในภาพซ้าย และเส้นสีฟ้ากับเส้นสีเขียวในภาพกลาง). ภาพล่างขวา แสดงค่าความน่าจะเป็นของส่วนผสมทั้งค่าที่ทำนาย (ใช้สัญลักษณ์ `i=a` และ `i=b` สำหรับ `mode a` และ `mode b` ตามลำดับ) และค่าเฉลย (ใช้สัญลักษณ์ `I=0` และ `I=1` สำหรับ `mode 0` และ `mode 1` ตามลำดับ).

ผลลัพธ์การเรียนค่าเบี่ยงเบนมาตราฐาน. ภาพซ้ายและกลาง แสดง จุดข้อมูล (จุดสีเทา) และค่าเบี่ยงเบนมาตราฐาน ที่แทนด้วยความหนาของพื้นที่แรเงา. ภาพขวา แสดงค่าเบี่ยงเบนมาตราฐาน ในแกนตั้ง และค่าตัวแปรต้น x ในแกนนอน. ค่าเบี่ยงเบนมาตราฐานที่ทำนาย ใช้สัญลักษณ์ sigma a และ sigma b สำหรับ mode a และ mode b ตามลำดับ. ค่าเบี่ยงเบนมาตราฐานของเฉลย ใช้สัญลักษณ์ sigma 0 และ sigma 1 สำหรับ mode 0 และ mode 1 ตามลำดับ. — ผลลัพธ์การเรียนค่าเบี่ยงเบนมาตราฐาน. ภาพซ้ายและกลาง แสดง จุดข้อมูล (จุดสีเทา) และค่าเบี่ยงเบนมาตราฐาน ที่แทนด้วยความหนาของพื้นที่แรเงา. ภาพขวา แสดงค่าเบี่ยงเบนมาตราฐาน ในแกนตั้ง และค่าตัวแปรต้น $x$ ในแกนนอน. ค่าเบี่ยงเบนมาตราฐานที่ทำนาย ใช้สัญลักษณ์ `sigma a` และ `sigma b` สำหรับ `mode a` และ `mode b` ตามลำดับ. ค่าเบี่ยงเบนมาตราฐานของเฉลย ใช้สัญลักษณ์ `sigma 0` และ `sigma 1` สำหรับ `mode 0` และ `mode 1` ตามลำดับ.

5.0.0.8 การกำหนดค่าเริ่มต้น.

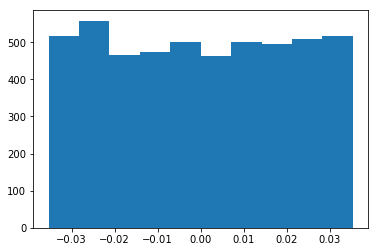
เมื่อเราทำการสร้างตัวแปร ค่าของตัวแปรจะถูกกำหนดขึ้นมาด้วย เช่น คำสั่งกำหนดค่า fc1 = torch.nn.Linear(800,5000) จะสร้างพารามิเตอร์ของชั้นคำนวณ ได้แก่ fc1.weight และ fc1.bias ซึ่งเป็นเทนเซอร์ สัดส่วน $(800,5000)$ และ $(5000)$ ตามลำดับ พร้อมค่าเริ่มต้น. โดยดีฟอลต์ของไพทอร์ช ค่าเริ่มต้นทั้งของค่าน้ำหนักและไบอัส จะถูกกำหนดดังเช่นสมการ $\eqref{eq: standard init}$ นั่นคือ $\theta \sim \mathcal{U}(-\frac{1}{\sqrt{m_i}}, -\frac{1}{\sqrt{m_i}})$ เมื่อ $\theta$ คือค่าน้ำหนักหรือไบอัสแต่ละค่า และ $m_i$ คือจำนวนแผ่เข้าของชั้นคำนวณ. ตัวอย่างนี้ $m_i = 800$ และหากตรวจสอบการกระจายของค่าเริ่มต้นที่สร้างขึ้น ด้วยคำสั่ง เช่น plt.hist(fc1.bias.detach()) จะเห็นแผนภูมิแท่งคล้ายตัวอย่างในรูป 9 (ภาพ ก). สังเกต ค่าต่ำสุดสูงสุดประมาณ $-0.035$ และ $0.035$ ($\frac{1}{\sqrt{800}} \approx 0.035$).

$การแจกแจงค่าเริ่มต้นของไบอัส. ภาพ ก. b \sim \mathcal{U}(-0.035, 0.035) และภาพ ข. b \sim \mathcal{U}(-0.01, 0.01)$	$การแจกแจงค่าเริ่มต้นของไบอัส. ภาพ ก. b \sim \mathcal{U}(-0.035, 0.035) และภาพ ข. b \sim \mathcal{U}(-0.01, 0.01)$
ก.	ข.

หากต้องการกำหนดค่าเริ่มต้นนี้เป็นอื่นก็สามารถทำได้ ดังตัอย่างคำสั่งเช่น

with torch.no_grad():        
    fc1.bias.data = 2*0.01*torch.rand(800) - 0.01

เปลี่ยนค่าไบอัสเป็น $b \sim \mathcal{U}(-0.01, 0.01)$ ซึ่งเมื่อตรวจสอบ จะเห็นภาพคล้ายตัวอย่างในรูป 9 (ภาพ ข). หมายเหตุ จุดสำคัญอยู่ที่ค่าสูงสุดต่ำสุด ไม่ใช่ความสูงต่ำของแผนภูมิแท่งแต่ละแท่ง (ที่โดยรวมแสดงการแจกแจงเอกรูป แต่จำนวนข้อมูลที่น้อย $800$ ค่า อาจทำให้เห็นความไม่สมดุลของแต่ละแท่งบ้าง).

การกำหนดค่าเริ่มต้นให้กับโครงข่ายประสาทเทียม อาจทำได้ดังตัวอย่าง

[language=Python, , caption={[ตัวอย่างการกำหนดค่าเริ่มต้นให้โครงข่ายประสาทเทียม]ตัวอย่างการกำหนดค่าเริ่มต้นให้โครงข่ายประสาทเทียม}, 
label={code: torch init net}]
with torch.no_grad():        
    net.fc1.bias.data = torch.rand(net.fc1.bias.shape)
    net.fc2.bias.data = torch.rand(net.fc2.bias.shape)

เมื่อ net เป็นตัวแปรแทนโครงข่ายประสาทเทียม ที่มีชั้นคำนวณ fc1 และ fc2 และต้องการกำหนดค่าเริ่มต้นของไบอัสแต่ละค่า ให้เป็นค่าสุ่มจากการแจกแจงเอกรูป $\mathcal{U}(0, 1)$. การกำหนดค่าน้ำหนักก็สามารถทำได้ในลักษณะเดียวกัน.

อย่างไรก็ตาม เพื่อความสะดวก สำหรับการกำหนดค่าเริ่มต้นชั้นคำนวณต่าง ๆ ด้วยวิธีเดียวกัน เมท็อด apply ของ nn.Module ¹³ สามารถช่วยลดภาระ การโปรแกรมซ้ำซ้อนลงได้ ดังคำสั่ง

with torch.no_grad():        
    net.apply(initx)

เมื่อ net คือตัวแปรโครงข่ายประสาทเทียมที่ต้องการกำหนดค่าน้ำหนักเริ่มต้น และ initx คือฟังก์ชันกำหนดค่าเริ่มต้นที่ต้องการใช้กับค่าน้ำหนัก (และไบอัส) ทุกชั้นคำนวณ. รายการ [code: xavier init] แสดงตัวอย่างโปรแกรมของฟังก์ชันที่ใช้กำหนดค่าน้ำหนักและไบอัส (วิธีเซเวียร์ ดูสมการ $\eqref{eq: xavier initialization}$ ประกอบ). เนื่องจาก เมท็อด apply จะรันฟังก์ชันกับทุก ๆ มอดูลย่อยของ net (ตัวอย่างข้างต้น คือ fc1 และ fc2) และตัวของ net เอง ดังนั้น ในฟังก์ชันที่จะใช้กำหนดค่าเริ่มต้น จึงต้องทำการเลือกกรณี (ตรวจสอบ type(m)) เพื่อจะดำเนินการได้ถูกต้อง.

[language=Python, , caption={[ฟังก์ชันกำหนดค่าน้ำหนักเริ่มต้นเซเวียร์]ฟังก์ชันกำหนดค่าน้ำหนักเริ่มต้นเซเวียร์
}, 
label={code: xavier init}]
def initx(m): # xavier initialization
    if type(m) == nn.Linear:        
        no, ni = m.weight.data.size()
        s = torch.sqrt(torch.Tensor([6/(ni + no)]))
        m.weight.data = 2*s*torch.rand(no, ni) - s
        m.bias.data = 0.1*torch.randn(m.bias.data.size())

5.0.0.8.1 แบบฝึกหัด

จากตัวอย่างวิธีกำหนดค่าเริ่มต้น จงเขียนโปรแกรมกำหนดค่าเริ่มต้นแบบไคมิง แล้วศึกษางานของโกลโรต์และเบนจิโอ จากนั้น เลือกชุดข้อมูล ออกแบบการทดลอง เพื่อศึกษาผลกระทบจากฟังก์ชันกระตุ้น และวิธีการกำหนดค่าเริ่มต้น แล้วนำเสนอสิ่งที่ได้เรียนรู้ อภิปราย และสรุปผล.

ตัวอย่างนำเสนอผลและอภิปราย. รูป 12 แสดงตัวอย่างผลที่คาดว่า เป็นส่วนหนึ่งที่ทำให้โกลโรต์และเบนจิโอ ตั้งสมมติฐานว่า หากความแปรปรวนของค่าน้ำหนัก ที่ชั้นต่าง ๆ มีค่าใกล้เคียงกัน จะช่วยให้การฝึกทำได้ง่ายขึ้น. สังเกตว่า ในกรณีที่การฝึกทำได้ดี ความห่างระหว่างเปอร์เซ็นไทล์ที่ 25 และ 75 (สื่อถึงความแปรปรวน) ของชั้นคำนวณต่าง ๆ จะมีความห่างใกล้เคียงกัน แต่อาจจะมีการขยายไล่เป็นชั้น ๆ จากชั้นต้น ๆ ที่จะขยายก่อนและไล่ไปชั้นหลัง ๆ ซึ่งต่างจากผลที่เห็น ในกรณีการฝึกล้มเหลว ที่ความแปรปรวนระหว่างชั้นคำนวณต่างกันอย่างชัดเจน นอกจากนั้น ก็ยังไม่เห็นการขยายของความแปรปรวน.

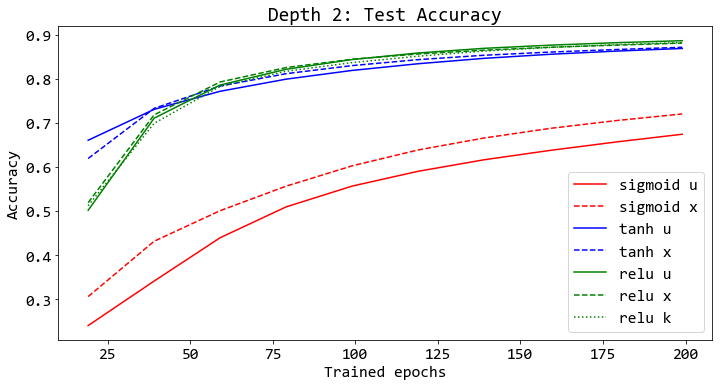
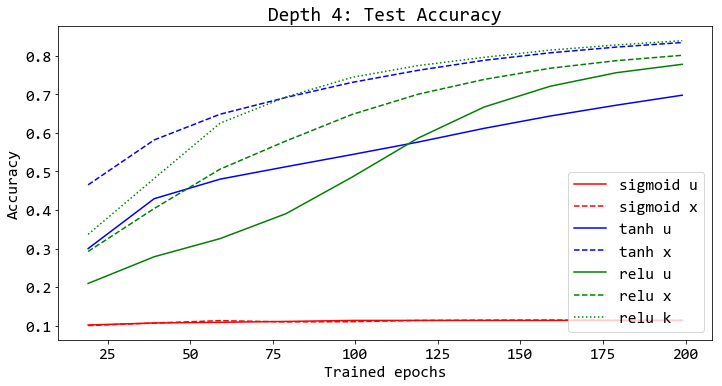
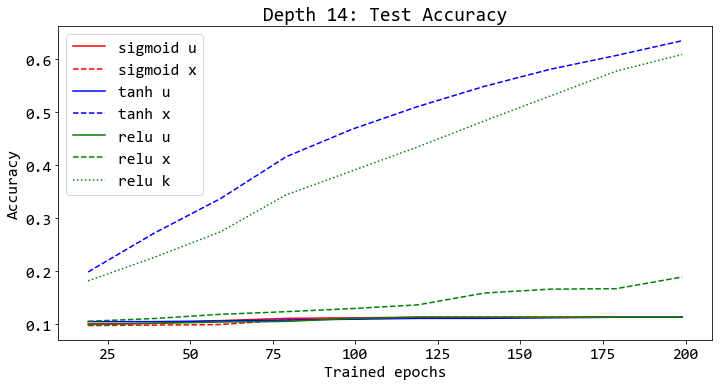
รูป 15 แสดงตัวอย่างผลสรุปที่สำคัญ ได้แก่ (1) ฟังก์ชันกระตุ้น tanh และ relu ทำงานดีกว่า sigmoid ไม่ว่าจะใช้โครงข่ายที่มีความลึกเท่าใด. (2) ผลดีจากการกำหนดค่าเริ่มต้นด้วยวิธีเซเวียร์และไคมิง (สัญกรณ์ย่อ x และ k ในภาพ) จะเห็นชัดเจนขึ้น เมื่อใช้งานกับโครงข่ายที่ลึกขึ้น. (3) ทั้งวิธีเซเวียร์ และวิธีไคมิน ให้ผล ดังที่คาดหมาย นั่นคือ วิธีเซเวียร์ ช่วยในกรณี tanh เมื่อเปรียบเทียบกับวิธีพื้นฐาน (สมการ $\eqref{eq: standard init}$ สัญกรณ์ย่อ u ในภาพ). และวิธีไคมิน ช่วยในกรณี relu เมื่อเปรียบเทียบกับทั้งวิธีเซเวียร์และวิธีพื้นฐาน. สังเกตว่า ทั้งวิธีเซเวียร์และวิธีไคมินพัฒนา โดยอาศัยสมมติฐานเชิงเส้น ที่แม้จะไม่ตรงกับสถานการณ์จริง แต่ในทางปฏิบัติ กลับพบว่า ทั้งสองวิธีทำงานได้ดีอย่างชัดเจน.

นอกจาก ผลสรุปเรื่องวิธีการกำหนดค่าเริ่มต้น อีกประเด็นหนึ่งที่โกลโรต์และเบนจิโอได้ศึกษา ก็คือ การตรวจดูค่าโดยรวม ของผลการกระตุ้นและค่าเกรเดียนต์ระหว่างฝึก (ดังเช่นที่แสดงในรูป 12) และตรวจสอบการแจกแจงของผลการกระตุ้นภายหลังการฝึก (ดังเช่นรูป 16) ที่ทั้งคู่คิดว่าน่าจะช่วยให้สามารถทำความเข้าใจพฤติกรรมการเปลี่ยนแปลงของโครงข่ายจากการฝึกได้ดีขึ้น.

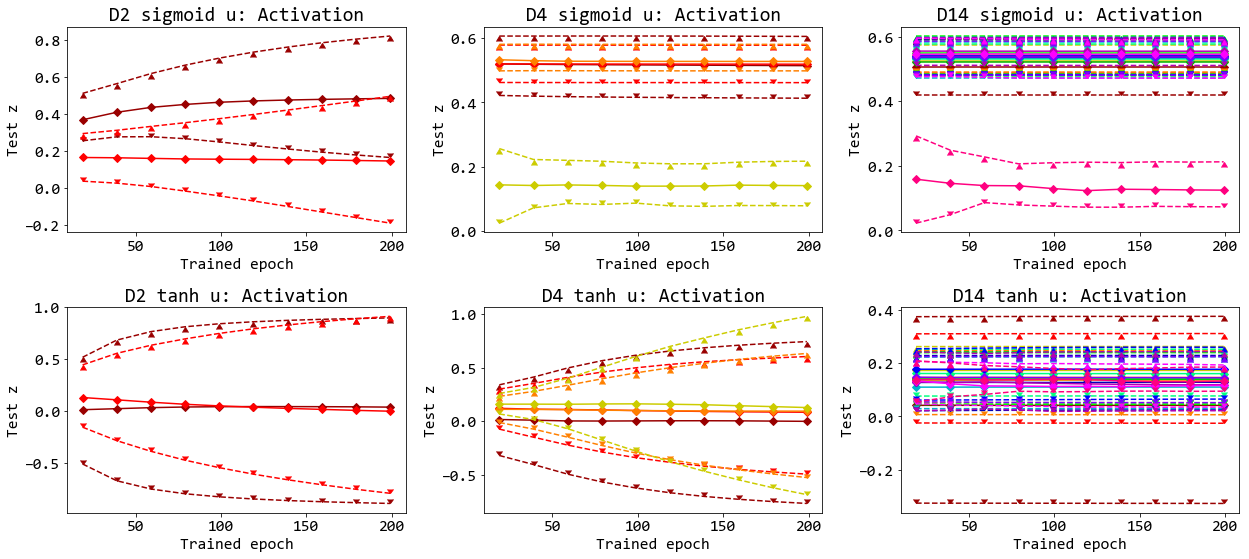
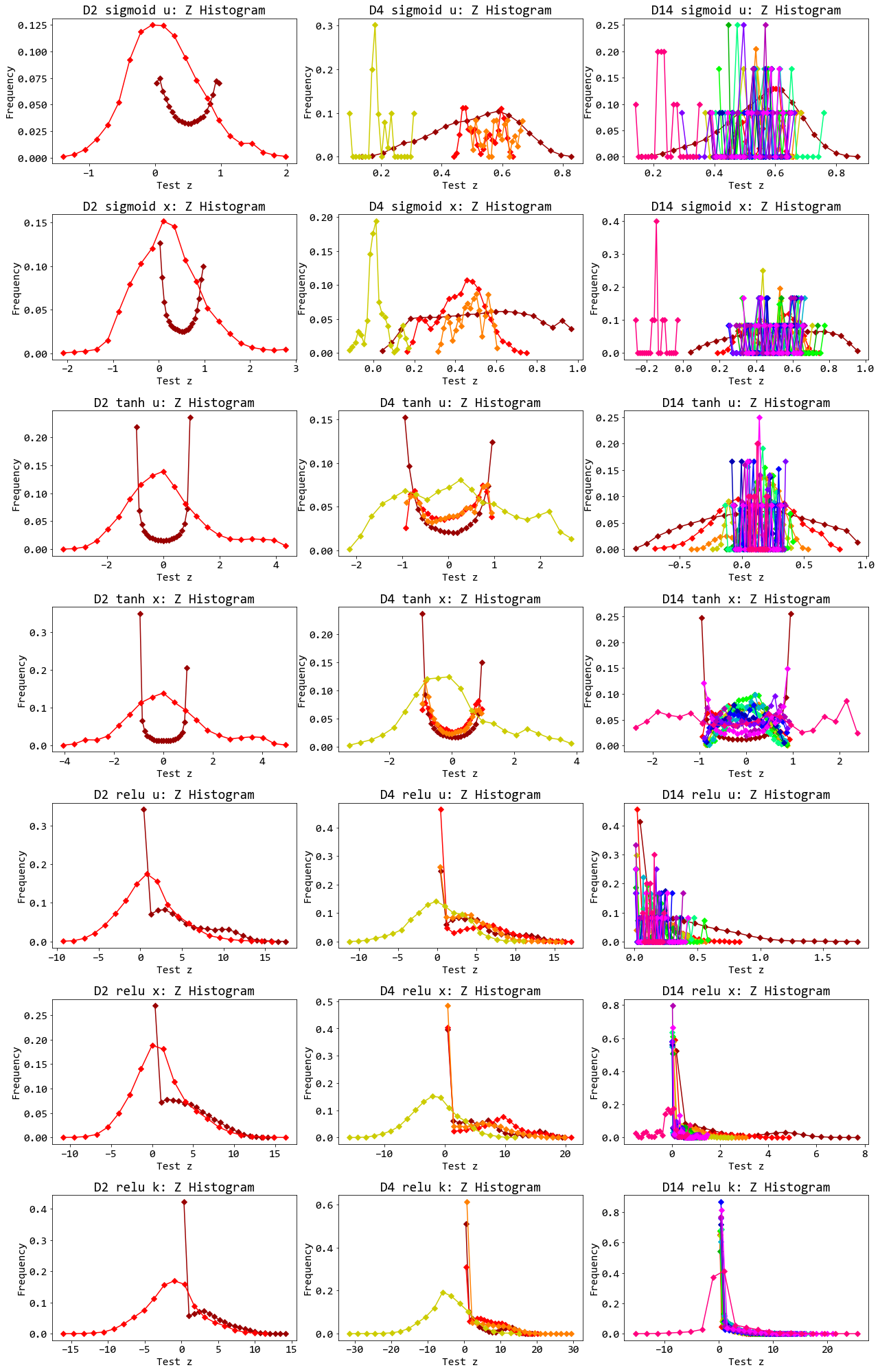
รูป 16 แสดงให้เห็นว่า กรณีที่การฝึกทำได้ดี (โครงข่ายสองชั้นทุกแบบ, โครงข่ายสี่ชั้น เมื่อใช้ tanh หรือ relu, โครงข่ายสิบสี่ชั้น เมื่อใช้ tanh และวิธีเซเวียร์ หรือเมื่อใช้ relu และวิธีไคมิง. ดูรูป 15 ประกอบ) หน่วยคำนวณส่วนใหญ่ (ในเกือบทุกกรณี ยกเว้น tanh และวิธีเซเวียร์) อยู่ในระดับอิ่มตัว (saturation) นั่นคือ ค่าผลการกระตุ้น $z = 0$ หรือ $z = 1$ สำหรับฟังก์ชันซิกมอยด์, ค่าการกระตุ้น $z = -1$ หรือ $z = 1$ สำหรับฟังก์ชันไฮเปอร์บอลิกแทนเจนต์, และค่าการกระตุ้น $z = 0$ สำหรับเรลู.

$ค่าความแม่นยำกับข้อมูลทดสอบ เมื่อใช้โครงข่ายความลึก 2 ชั้น (ภาพบนสุด) 4 ชั้น (ภาพกลาง) และ 14 ชั้น (ภาพล่าง) ประกอบกับฟังก์ชันกระตุ้นในชั้นซ่อนแบบต่างๆ (sigmoid ซิกมอยด์, tanh ไฮเปอร์บอลิกแทนเจนต์, และ relu เรลู ) และวิธีกำหนดค่าเริ่มต้นแบบต่าง ๆ (u วิธีพื้นฐาน สมการ \eqref{eq: standard init}, x วิธีเซเวียร์ สมการ \eqref{eq: xavier initialization}, และ k วิธีไคมิง สมการ \eqref{eq: kaiming init}). ค่าความแม่นยำที่แสดง เป็นค่าเฉลี่ยจากการทำซ้ำสิบครั้ง.$

แต่ละภาพ แสดงการแจกแจงของค่าการกระตุ้น สำหรับแต่ละกรณี (ความลึก ฟังก์ชันกระตุ้นที่ใช้ และวิธีกำหนดค่าเริ่มต้น ระบุเหนือแต่ละภาพ ด้วยรหัสเช่นเดียวกับรูป 12 และ 15). แกนนอน แสดงค่าผลการกระตุ้น และแกนตั้ง แสดงค่าความถี่หารด้วยจำนวนทั้งหมด.

หมายเหตุ การฝึกเขียนโปรแกรมเอง (เช่น รายการ [code: xavier init]) จะช่วยให้เข้าใจกลไกภายในได้ดี แต่การใช้งานในทางปฏิบัติ การใช้ฟังก์ชันสำเร็จรูป จะช่วยเพิ่มความสะดวกในการทำงานและการสื่อสารได้ดีขึ้น (โดยเฉพาะในกรณีทำงานด้วยกันหลายคน). ไพทอร์ชมีฟังก์ชันสำเร็จรูป สำหรับการกำหนดค่าเริ่มต้นด้วยวิธีที่รู้จักดีต่างๆ รวมถึงวิธีเซเวียร์และไคมิง เช่น nn.init.xavier_uniform_(w) สำหรับการกำหนดค่าน้ำหนักเริ่มต้นให้กับพารามิเตอร์ w ด้วยวิธีเซเวียร์.

5.0.0.8.2 แบบฝึกหัด

จงเลือกขั้นตอนวิธีการฝึก จากวิธีลงเกรเดียนต์กับกลไกโมเมนตัม, วิธีอาร์เมเอสพรอป, วิธีอาร์เมเอสพรอป กับกลไกโมเมนตัม, วิธีอดัม หรือวิธีอื่น ๆ ที่สนใจ แล้วเขียนโปรแกรมวิธีดังกล่าว เปรียบเทียบผลการทำงานกับโปรแกรมสำเร็จของวิธีนั้น (ได้แก่ optim.SGD, optim.RMSprop, และ optim.Adam) และเปรียบเทียบกับวิธีลงเกรเดียนต์ เลือกชุดข้อมูลขึ้นมาเพื่อทดสอบ ออกแบบการทดลอง เพื่อวัดผลทั้งในเชิงความเร็วและคุณภาพในการเรียนรู้ รวมถึงความทนทานต่อค่าอภิมานพารามิเตอร์ต่างๆที่เลือกใช้ และความทนทานกับการกำหนดค่าเริ่มต้นแบบต่างๆ อภิปราย และสรุป.

5.0.0.8.3 แบบฝึกหัด

จงออกแบบการทดลอง เพื่อทดสอบการทำงานของแบชนอร์ม วัดผลทั้งในความเร็วในการฝึก คุณภาพการฝึก ความทนทานต่อค่าอัตราการเรียนรู้ ผลจากขนาดของหมู่เล็ก รวมถึงตำแหน่งที่ทำแบชนอร์ม (ทำที่ตัวกระตุ้น นั่นคือก่อนฟังก์ชันกระตุ้น เปรียบเทียบกับทำที่ผลการกระตุ้น นั่นคือหลังฟังก์ชันกระตุ้น) ทดลองเขียนโปรแกรมแบชนอร์ม (ตัวอย่างแสดงในรายการ [code: class MyBN]) และเปรียบเทียบกับโปรแกรมแบชนอร์มสำเร็จรูป (เช่น คำสั่ง self.bn1 = nn.BatchNorm1d(8) เปรียบเทียบกับ self.bn1 = MyBN(8) ในรายการ [code: ann batch norm] เมื่อ MyBN กำหนดดังแสดงในรายการ [code: class MyBN]). สังเกตผล อภิปราย และสรุป.

[language=Python, , caption={[ตัวอย่างโปรแกรมโครงข่ายประสาทเทียมที่ใช้แบชนอร์ม]ตัวอย่างโปรแกรมโครงข่ายประสาทเทียมที่ใช้แบชนอร์ม.
แบชนอร์มเหมือนชั้นคำนวณที่เพิ่มขึ้น.
คลาส \texttt{MyBN} เป็นชั้นคำนวณแบชนอร์ม กำหนดดังแสดงในรายการ~\ref{code: class MyBN}.
หมายเหตุ การใช้แบชนอร์ม ทำให้ไบอัสเกินความจำเป็นและซ้ำซ้อน
และสามารถตัดออกได้.
แต่ในตัวอย่างนี้ไม่ได้ตัดค่าไบอัสออก.
หากต้องการตัดไบอัสออก สามารถทำได้โดยคำสั่ง เช่น \texttt{self.fc1 = nn.Linear(1, 8, bias=False)}
}, label={code: ann batch norm}]
class MyNetManualBN(nn.Module):
    def __init__(self):
        super(MyNetManualBN, self).__init__()        
        self.fc1 = nn.Linear(1, 8)
        self.bn1 = MyBN(8)
        self.fc2 = nn.Linear(8, 8)
        self.bn2 = MyBN(8)
        self.fc3 = nn.Linear(8, 1)

    def forward(self, x):
        self.a1 = self.fc1(x)
        self.b1 = self.bn1(self.a1)
        self.z1 = torch.relu(self.b1)
        self.a2 = self.fc2(self.z1)
        self.b2 = self.bn2(self.a2)
        self.z2 = torch.relu(self.b2)
        self.z3 = self.fc3(self.z2)
        return self.z3

class MyBN(nn.Module):
    def __init__(self, num_features, eps=1e-5, momentum=0.1):
        super(MyBN, self).__init__()
        self.num_features = num_features
        self.eps = eps
        self.momentum = momentum
        self.weight = nn.Parameter(torch.ones(num_features))
        self.bias = nn.Parameter(torch.zeros(num_features))
        self.register_buffer('running_mean', torch.zeros(num_features))
        self.register_buffer('running_var', torch.ones(num_features))                

    def forward(self, z):
        mu = self.running_mean
        svar = self.running_var
        if self.training:
            with torch.no_grad():
                mu = torch.mean(z, dim=0)
                svar = torch.var(z, dim=0)
            # Tracing running_mean and running_var
            p = self.momentum
            q = 1 - p
            self.running_mean = p*mu + q*self.running_mean
            self.running_var = p*svar + q*self.running_var            
        # end self.training        
        zn = (z - mu)/torch.sqrt(svar + self.eps)
        zns = zn * self.weight + self.bias
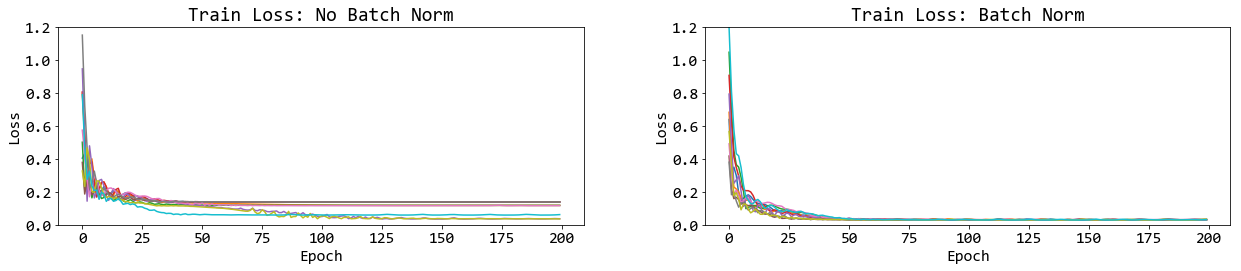
        return zns

รูป 17, 18, 19, และ 20 แสดงตัวอย่างการนำเสนอผล. รูป 17 แสดงค่าสูญเสียระหว่างการฝึก จากการทดสอบสิบซ้ำ ภาพซ้าย เมื่อไม่ได้ใช้แบชนอร์ม และภาพขวา เมื่อใช้แบชนอร์ม. เห็นได้ชัดเจนว่า แบชนอร์มช่วยให้การฝึกทำได้เร็วขึ้นและแน่นอนขึ้น.

รูป 18 แสดงค่าทดสอบ ซึ่งในที่นี้ใช้ค่าเฉลี่ยกำลังสองน้อยที่สุด. ภาพแสดงด้วยแผนภูมิกล่อง กล่องซ้ายสุด แสดงค่าผิดพลาด เมื่อไม่ใช้แบชนอร์ม. กล่องกลาง เมื่อใช้แบชนอร์ม (ทำที่ตัวกระตุ้น นั่นคือ ใช้ ทำที่ $\boldsymbol{A}$ เมื่อ ชั้นคำนวณ ทำ $h(\boldsymbol{A})$ โดย $\boldsymbol{A} = \boldsymbol{W} \cdot \boldsymbol{Z} + \boldsymbol{b}$ หรือ ทำก่อนเข้าฟังก์ชันกระตุ้น). กล่องขวา เมื่อใช้แบชนอร์ม แต่ทำแบชนอร์มที่ผลการกระตุ้น แทนที่จะทำที่ตัวกระตุ้น (นั่นคือ ทำที่ $\boldsymbol{Z}$ หรือทำหลังฟังก์ชันกระตุ้น). รูป 18 แสดงในเห็นว่า ไม่เพียงแต่ แบชนอร์มช่วยให้การฝึกดำเนินการได้เร็วขึ้น แบชนอร์มยังช่วยคุณภาพการฝึกด้วย และเพื่อให้ได้ประสิทธิภาพที่ดี การทำแบชนอร์มควรทำที่ค่าตัวกระตุ้น (ค่าก่อนเข้าฟังก์ชันกระตุ้น).

ค่าฟังก์ชันสูญเสียต่อสมัยฝึก จากการทดสอบซ้ำ 10 ครั้ง เมื่อไม่ใช้แบชนอร์ม (ภาพซ้าย) และใช้แบชนอร์ม (ภาพขวา).

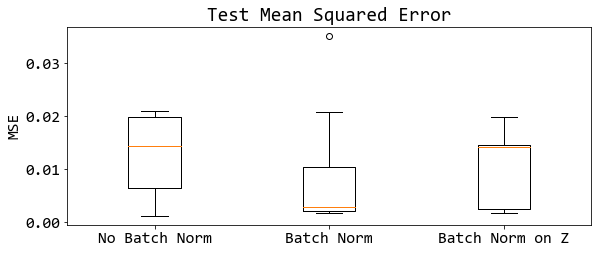
แผนภูมิกล่อง แสดงค่าเฉลี่ยค่าผิดพลาดกำลังสอง จากการทดสอบ 10 ครั้ง เมื่อไม่ใช้แบชนอร์ม (กล่องซ้าย), เมื่อใช้ (กล่องกลาง) และเมื่อใช้แบชนอร์ม แต่ทำแบชนอร์มที่ผลการกระตุ้น (กล่องขวา).

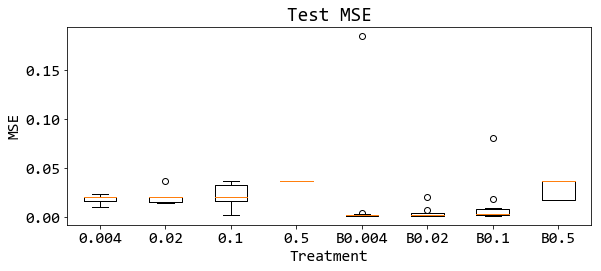
แผนภูมิกล่องแสดงค่าเฉลี่ยค่าผิดพลาดกำลังสอง จากการทดสอบ 10 ครั้ง เมื่อไม่ใช้แบชนอร์ม และเมื่อใช้แบชนอร์ม กับอัตราเรียนรู้ต่าง ๆ. ตัวเลขที่แสดง หมายถึง ค่าอัตราเรียนรู้ที่ใช้ และอักษร B ที่กำกับหมายถึง มีการใช้แบชนอร์ม. — แผนภูมิกล่องแสดงค่าเฉลี่ยค่าผิดพลาดกำลังสอง จากการทดสอบ 10 ครั้ง เมื่อไม่ใช้แบชนอร์ม และเมื่อใช้แบชนอร์ม กับอัตราเรียนรู้ต่าง ๆ. ตัวเลขที่แสดง หมายถึง ค่าอัตราเรียนรู้ที่ใช้ และอักษร `B` ที่กำกับหมายถึง มีการใช้แบชนอร์ม.

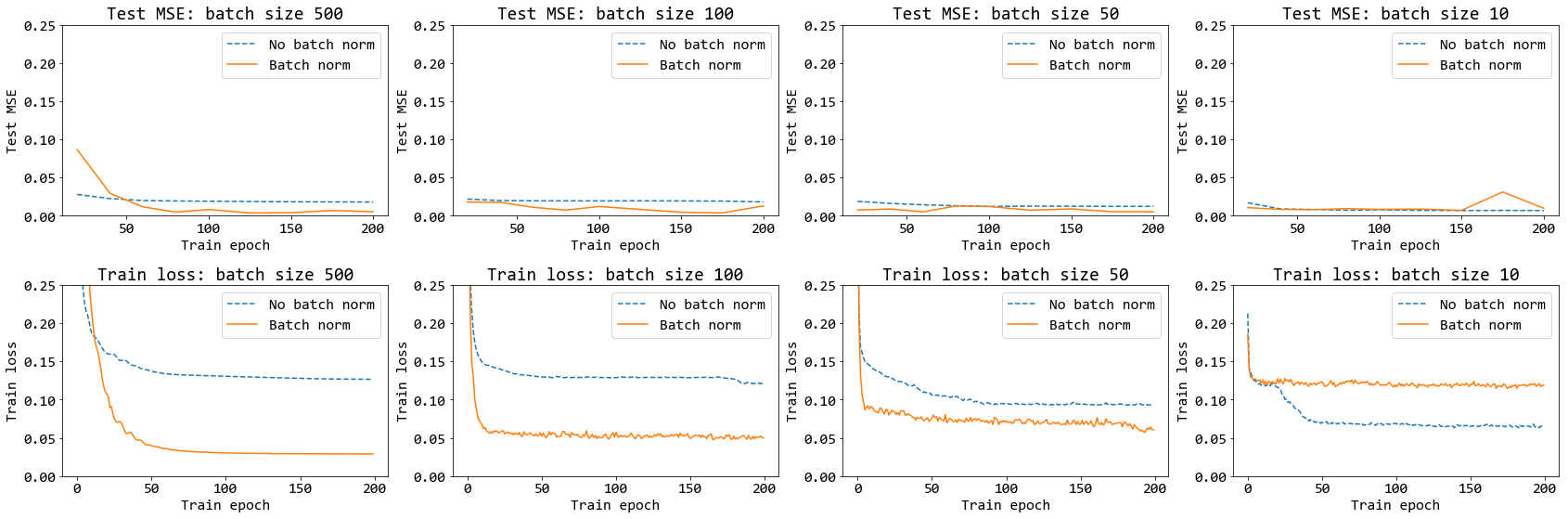
ค่าเฉลี่ยค่าผิดพลาด ระหว่างการฝึก เมื่อใช้และไม่ใช้แบชนอร์ม ที่ขนาดหมู่เล็กต่าง ๆ (ภาพต่าง ๆ ในแถวบน). ค่าเฉลี่ยค่าฟังก์ชันสูญเสีย ระหว่างการฝึก เมื่อใช้และไม่ใช้แบชนอร์ม ที่ขนาดหมู่เล็กต่าง ๆ (ภาพต่าง ๆ ในแถวล่าง). .

แผนภาพกล่อง แสดงค่าผิดพลาด จากการทดสอบ 10 ครั้ง เมื่อใช้และไม่ใช้แบชนอร์ม กับขนาดหมู่เล็กต่าง ๆ.

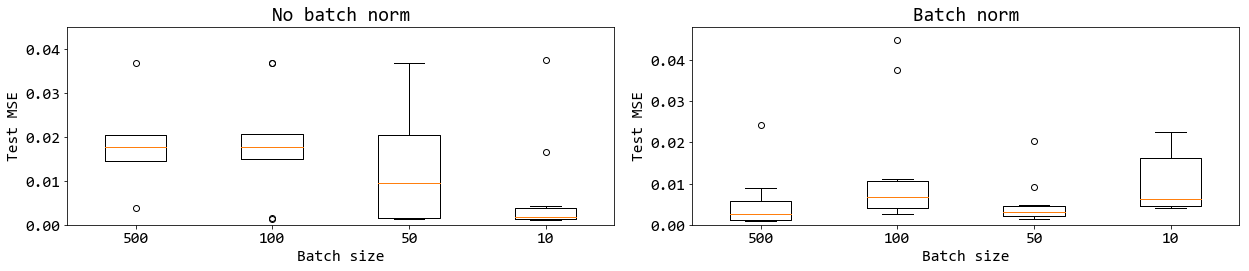
แผนภาพกล่อง แสดงค่าผิดพลาด จากการทดสอบ 10 ครั้ง เมื่อใช้ขนาดหมู่เล็กต่าง ๆ ในกรณีที่ใช้และไม่ใช้แบชนอร์ม. เปรียบเทียบกับรูป 21 รูปนี้นำเสนอจากอีกมุมมองหนึ่ง นั่นคือ การเลือกใช้หรือไม่ใช้แบชนอร์ม ควรพิจารณาประกอบกับขนาดของหมู่เล็กที่จะเลือกใช้ด้วย.

ภาพซ้าย แสดงการทำงานของแบชนอร์มกับการเลื่อนของความแปรปรวนร่วมเกี่ยวภายนอก. อัตราการปรับปรุงคุณภาพการทำนายเมื่อใช้แบชนอร์มเทียบกับไม่ใช้ แสดงด้วยเส้นประสีแดง โดย ค่าเป็นบวกหมายถึงคุณภาพดีขึ้นเมื่อใช้แบชนอร์ม ศูนย์หมายถึงคุณภาพเท่ากัน และค่าเป็นลบหมายถึงคุณภาพแย่ลง. เส้นทึบสีน้ำเงิน แสดงค่ามากที่สุดของความต่างระหว่างค่าเฉลี่ยของหมู่กับ ค่าเฉลี่ยของข้อมูลทั้งหมด (ความต่างคิดเป็นค่าสัมบูรณ์). ภาพขวา แสดงค่ามากที่สุดของความต่าง (แกนนอน) กับเปอร์เซ็นต์การปรับปรุงคุณภาพเมื่อใช้แบชนอร์ม (แกนตั้ง).

รูป 19 แสดงให้เห็นว่า แบชนอร์มทำงานได้ดีที่ค่าอัตราเรียนรู้ต่าง ๆ. รูป 20 แสดง การทำงานของแบชนอร์ม ในสถานการณ์ของขนาดหมู่เล็กต่าง ๆ ในช่วงสมัยฝึกต่าง ๆ. สังเกตว่า เมื่อใช้หมู่เล็กขนาดเล็กเกินไป (ภาพขวาสุด บนและล่าง) แบชนอร์มทำงานได้ไม่ดี และนำไปสู่การฝึกที่แย่กว่าการฝึกที่ไม่ใช้แบชนอร์ม. รูป 21 แสดงค่าความผิดพลาดเมื่อนำแบบจำลองที่ฝึกไปทดสอบ. รูป 21 ยืนยันว่า หากใช้แบชนอร์ม แล้วเลือกขนาดหมู่เล็กที่เล็กเกินไป จะทำให้ผลการฝึกแย่ลงได้.

แบชนอร์ม ออกแบบมาเพื่อแก้ไขการเลื่อนของความแปรปรวนร่วมเกี่ยวภายใน ที่เกิดจากการปรับค่าพารามิเตอร์ระหว่างการฝึก แต่การทำแบชนอร์ม ที่ปรับค่าเฉลี่ยและความแปรปรวนของหมู่เล็ก ก็เสี่ยงที่จะทำสารสนเทศจากข้อมูลเสียหาย. หากความต่างของค่าเฉลี่ยและความแปรปรวนระหว่างหมู่ มาจากตัวข้อมูลเอง ไม่ใช่มาจากการเปลี่ยนแปลงของค่าพารามิเตอร์ในชั้นคำนวณก่อนหน้า.

หากการแจกแจงสารสนเทศของข้อมูลในหมู่เล็กแต่ละหมู่ ค่อนข้างคงเส้นคงวา และสามารถแทนการแจกแจงสารสนเทศของข้อมูลโดยรวมได้ การเลื่อนของค่าเฉลี่ยและความแปรปรวนระหว่างหมู่ มาจากการเปลี่ยนแปลงของค่าพารามิเตอร์ของชั้นคำนวณก่อนหน้า การทำแบชนอร์มจะมีประสิทธิผลตามที่ออกแบบไว้.

แต่หากการเลื่อนของค่าเฉลี่ยและความแปรปรวนระหว่างหมู่ มาจากสารสนเทศที่ต่างกันของข้อมูลระหว่างหมู่เอง ความเสี่ยงของการทำ จะสูงขึ้นมาก และเมื่อประกอบกับแนวทางปฏิบัติของการสุ่มหมู่เล็ก ที่มักทำการสุ่มแค่ครั้งแรก และใช้ลำดับและการจัดกลุ่มนั้นตลอด ยิ่งจะซ้ำเติมความเสี่ยงนี้เข้าไปอีก.

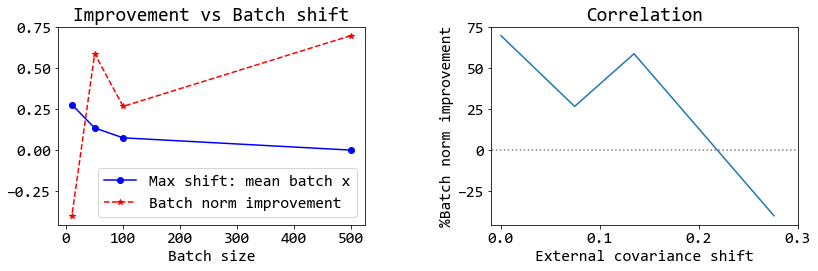
ตัวอย่างของกรณีที่ใช้ขนาดหมู่เล็กเป็นสิบ ภาพขวาสุดที่แสดงในรูป 21 แสดงให้เห็นว่า เมื่อขนาดหมู่เล็กลง โอกาสที่การแจกแจงสารสนเทศของข้อมูลระหว่างหมู่จะะสม่ำเสมอหรือจะเป็นตัวแทนของข้อมูลทั้งหมดได้ จะน้อยลง และเมื่อการแจกแจงสารสนเทศของข้อมูลระหว่างหมู่ไม่สม่ำเสมอ การทำแบชนอร์มจึงทำสารสนเทศบางอย่างเสียหายไป และส่งผลให้การฝึกทำได้แย่. รูป 22 เปรียบเทียบให้เห็นว่า ความสัมพันธ์ระหว่างคุณภาพการฝึกกับขนาดของหมู่เล็ก เปลี่ยนไป เมื่อใช้แบชนอร์ม. ในทางปฏิบัติ หลายครั้ง ขนาดของหมู่เล็ก อาจถูกจำกัดจากหน่วยความจำ และการเลือกใช้หรือไม่ใช้แบชนอร์ม ควรคำนึงถึงความเสี่ยง จากประเด็นความสม่ำเสมอระหว่างหมู่เล็ก ของการแจกแจงสารสนเทศจากตัวข้อมูลเองประกอบ.

รูป 23 แสดงประเด็นความสัมพันธ์ระหว่างประสิทธิผลการทำงานของแบชนอร์มกับการแจกแจงข้อมูลระหว่างหมู่เล็ก. จากรูป เมื่อ การแจกแจงข้อมูลระหว่างหมู่เล็ก ทำให้เกิดความต่างระหว่างหมู่เล็กมาก ประสิทธิผลการทำงานของแบชนอร์มจะต่ำลง และอาจต่ำจนการใช้แบชนอร์มจะเป็นผลเสียมากกว่าผลดี ดังแสดงออกมาเป็นเปอร์เซ็นต์ปรับปรุงที่ติดลบ.

แล้วกรณีที่ข้อมูลมีรูปแบบแปลก ๆ ที่พบได้ยาก หรือกรณีประเด็นเรื่องวิธีประมาณค่า $\mu_i$ และ $\sigma_i^2$ ที่ใช้ทำแบชนอร์มภายหลังการฝึก อาจก่อให้เกิดความเสี่ยงอย่างไรบ้าง จงระดมความคิิด อภิปราย และสรุป.

5.0.0.8.4 แบบฝึกหัด

การศึกษาหัวข้อที่สนใจ. ¹⁴ บางครั้งในบางจังหวะเวลา ศาสตร์ที่เราศึกษา มีการเปลี่ยนแปลงพัฒนาที่รวดเร็วมาก และอาจจำเป็นต้องศึกษาความก้าวหน้าและพัฒนาการล่าสุดจากแหล่งอื่น ๆ เพิ่มเติม.

จงเลือกหัวข้อเรื่องที่สนใจ (เช่น การบรรยายภาพอัตโนมัติ, การแต่งเพลงอัตโนมัติ, การทำนายพฤติกรรมโปรตีน) แล้วศึกษา ทำความเข้าใจในหัวเรื่องดังกล่าว.

การศึกษา ทำความเข้าใจ อาจทำโดย (1) ค้นหาและรวบรวมแหล่งข้อมูล เกี่ยวกับหัวข้อที่สนใจ ซึ่งแหล่งข้อมูลอาจรวมถึง หนังสือ บทความวิชาการ บทความทั่วไป วีดีโอ เว็บเพจ เป็นต้น.

(2) ศึกษาแต่ละแหล่งข้อมูลที่ได้มาคร่าว ๆ (ถ้าเป็นบทความวิชาการ รวมถึงบทความวิจัย อย่างน้อย อ่านบทคัดย่อและบทนำ) และอาจจะทำบันทึกย่อ ว่า แต่ละแหล่งข้อมูลเกี่ยวข้องกับหัวข้อที่สนใจมากน้อยขนาดไหน และเราเข้าใจเนื้อหาเข้าใจมากน้อยขนาดไหน รวมถึงอาจจัดลำดับความสำคัญ และหมายเหตุถึงสิ่งที่คิดว่าจะดำเนินการต่อ เช่น ไม่ค่อยเกี่ยวข้อง ตัดทิ้งไปก่อน หรือ เกี่ยวข้องมาก ศึกษาให้เข้าใจ หรือ เกี่ยวข้องประมาณ $50\%$ พอเข้าใจแล้ว เก็บไว้เป็นตัวอย่าง หรือ ไม่แน่ใจว่าเกี่ยวข้อง เข้าใจดี ชอบเทคนิคที่เขาใช้ อาจใช้เป็นประโยชน์กับงานของเราได้ เก็บไว้อ้างอิงทีหลัง. หรือ ไม่แน่ใจว่าเกี่ยวข้อง ไม่ค่อยเข้าใจ เก็บไว้ดูอีกทีหลังจากเข้าใจหัวข้อนี้ดีขึ้น.

โดยทั่วไป ถ้าเป็นบทความวิชาการหรือบทความวิจัย ที่ไม่ใช่บทความทบทวน หรือไม่ใช่บทความสำรวจ เราอาจจะต้องอ่านตั้งแต่สามจนถึงสิบบทความ จึงอาจจะพอเข้าใจหัวข้อนั้นในระดับเบื้องต้นได้. นักศึกษาปริญญาเอก ซึ่งถูกคาดหวังว่าจะเข้าใจในหัวข้อเป็นอย่างดี อาจต้องอ่านบทความ ไม่น้อยกว่า $100$ บทความ. และก็ไม่แปลกที่จะเห็น บทความทบทวน หรือบทความสำรวจของหัวข้อใด ๆ ที่คณะผู้เขียนอาจต้องอ่านบทความต่าง ๆ ที่เกี่ยวข้องกับหัวข้อนั้น ๆ มากกว่า $300$ บทความ.

(3) หากไม่สามารถเข้าใจบทความวิชาการส่วนใหญ่ได้ ให้ระบุศาสตร์พื้นฐานที่อาจจะขาดไป เช่น บทความที่หนึ่ง เกี่ยวข้องมาก แต่ไม่เข้าใจเลย ดูเหมือนจะใช้ทฤษฎีความน่าจะเป็นและแคลคูลัสของการแปรผัน (calculus of variations). บทความที่สอง เกี่ยวข้อง แต่อ่านไม่เข้าใจ ใช้พีชคณิตเชิงเส้น, ความน่าจะเป็น และทฤษฎีสารสนเทศ. บทความที่ห้า เกี่ยวข้องมาก แต่ยังอ่านไม่เข้าใจ ใช้ทฤษฎีความน่าจะเป็น, กระบวนการ และการหาค่าดีที่สุด. บทความที่แปด เกี่ยวข้องบ้าง แต่อ่านไม่เข้าใจ เพราะประยุกต์ใช้กับงานชีวการแพทย์ ใช้การหาค่าดีที่สุด และชีวเคมี. เช่นนี้ ก็จะช่วยให้เราพอเห็นว่า เราขาดพื้นฐานอะไรไปบ้าง และเราสามารถจัดลำดับความสำคัญ และเลือกที่จะศึกษาพื้นฐานเหล่านี้ก่อน. หมายเหตุ เราไม่จำเป็นต้องสร้างพื้นฐานทุก ๆ อย่าง เช่น เราอาจเลือกว่า สิ่งที่เราสนใจไม่ได้เกี่ยวข้องกับงานชีวการแพทย์ เราอาจจะไม่เลือกเรียนรู้พื้นฐานด้านชีวเคมี ก็ได้ หรือ เราคิดว่าทฤษฎีกระบวนการสโทแคสติก มีใช้บ้างกับงานบางประเภท บางแนวทาง ซึ่งเราอาจจะยังไม่สนใจ ก็สามารถทำได้. แต่ระวังว่า หากอ่านบทความวิชาการไม่รู้เรื่อง และพบว่าพื้นฐานอะไรบ้างที่เราต้องการ แต่เราไม่อยากเรียนรู้พื้นฐานเหล่านั้นเลย (โดยเฉพาะพื้นฐานที่จำเป็น) อาจเป็นสัญญาณเตือนว่า จริง ๆ แล้ว ใจเราอาจจะไม่อยากศึกษาหัวข้อที่เลือกจริง ๆ.

(4) จากแหล่งข้อมูลที่ได้ศึกษาเบื้องต้น เลือกแหล่งที่เกี่ยวข้องมาก ๆ ออกมาศึกษาต่อ ให้ละเอียดขึ้น. สำหรับบทความวิจัย ให้ลองสรุปบทความ โดยระบุการค้นพบที่สำคัญ, วิธีที่ใช้, และคุณค่าเมื่อมองจากภาพรวมใหญ่ของหัวข้อ รวมถึงความสัมพันธ์กับงานอื่น ๆ. อาจอภิปรายประเด็นเพิ่มเติมด้วย เช่น ข้อจำกัด หรือศักยภาพ หรือการตีความจากมุมมองอื่น หรืออาจจะเป็นความเห็นส่วนตัว หรือสิ่งที่ชอบ ประเด็นที่ไม่ชอบ หากมี.

(5) ถ้าสามารถทำได้ หากลุ่มคนที่สนใจเรื่องเดียวกัน และอภิปรายเรื่องที่เรียนรู้ต่าง ๆ ด้วยกัน (อาจเป็นที่สามารถพบปะตัวต่อตัว หรือกลุ่มแบบออนไลน์ก็ได้). เรื่องที่จะอภิปรายอาจจะเลือกอย่างอิสระตามความสนใจของกลุ่ม หรือหากไม่รู้จะเริ่มจากเรื่องใด อาจลองพิจารณาจากคำถามเหล่านี้ เป้าหมายที่สำคัญของหัวข้อนี้คืออะไร? หัวข้อนี้มีศักยภาพและประโยชน์ต่อสังคมในวงกว้างอย่างไร? ความท้าทายที่สำคัญของหัวข้อนี้มีอะไรบ้าง? แนวทางและวิธีการต่าง ๆ ที่ใช้เพื่อจัดการกับความท้าทาย มีอะไรบ้าง? และแต่ละแนวทางมีข้อดีข้อเสียอะไร? งานเด่น ๆ ในหัวข้อดีมีอะไรบ้าง ทำไมมันถึงเด่นกว่างานอื่น ๆ? อะไรคือสิ่งที่คนในวงการนี้ สนใจและอยากได้มากที่สุด? ทำไมถึงอยากได้? ในความเห็นส่วนตัวแล้ว คิดว่า นอกจากแนวทางหลัก ๆ แล้ว มีแนวทางอื่นอีกไหม? แนวทางไหนบ้างที่น่าสนใจ และทำไม? เป็นต้น

คำแนะนำในการอ่านบทความวิจัย. ก่อนอ่าน อาจจะถามตัวเองว่า ต้องการอะไรบ้าง จากบทความที่กำลังจะอ่าน. หากมีสิ่งที่ต้องการรู้เฉพาะจากบทความ เช่น อยากรู้วิธีประเมินผล เมื่ออ่านก็ให้ความสำคัญเป็นพิเศษกับวิธีประเมินผล และหลังอ่านเสร็จให้กลับมาตอบตัวเอง ว่าได้รู้สิ่งที่ค้นหาว่าอย่างไร.

แต่หากเป็นการอ่านเพื่อความเข้าใจภาพโดยทั่วไป ไม่ได้มีประเด็นที่เจาะจงเป็นพิเศษ อาจลองวิธีดังนี้ (1) อ่านผ่าน ๆ รอบแรก โดยอ่านชื่อเรื่อง บทคัดย่อ และรูปภาพ. (2) อ่านบทนำ และบทสรุป แล้วดูรูปภาพและเนื้อหาส่วนอื่น ๆ คร่าว ๆ. (3) อ่านเนื้อหาต่าง ๆ ในบทความ โดยอาจจะยังไม่ต้องสนใจรายละเอียด โดยเฉพาะนิพจน์หรือสมการคณิตศาสตร์มากนัก. (4) ทำความเข้าใจส่วนต่าง ๆ รวมถึงพจน์ นิพจน์ และสมการคณิตศาสตร์ต่าง ๆ. (5) ตั้งคำถามกับตัวเอง เช่น บทความนี้พยายามศึกษาหรือแก้ปัญหาอะไรอยู่? แนวทางหรือวิธีที่ใช้ มันมีอะไรเป็นปัจจัยสำคัญ? เนื้อหาที่อ่านมีประโยชน์อะไรบ้างกับเรา? มีอ้างอิงรายการไหนบ้างที่เราอยากจะตามศึกษาต่อ? (6) หากสนใจบทความ อาจจะลองอภิปรายเพิ่มเติม เช่น ผลการศึกษาอาจมีข้อจำกัดอะไรบ้าง หรืออาจแสดงถึงศักยภาพอะไรบ้าง? จุดน่าสนใจ ความคิดสร้างสรรค์ของงานนี้ มีที่ใดบ้าง?

หลังอ่านจบแล้ว อาจลองทบทวนดูว่า มันช่วยตอบคำถามอะไรบ้างในภาพรวม ยังมีอะไรบ้างที่เป็นสิ่งที่เราสงสัยอยู่? สำหรับนักศึกษาปริญญาเอก หากสิ่งที่เราสงสัย เป็นสิ่งที่ในวงการก็ยังไม่รู้ (ศึกษาแหล่งข้อมูลให้มากพอ เพื่อแน่ใจว่า ในวงการยังไม่รู้) และเป็นสิ่งที่หากรู้แล้วจะมีประโยชน์ สิ่งนั้นอาจเป็นตัวเลือกที่น่าสนใจสำหรับหัวข้อวิจัยได้ ถ้าเราพอที่จะช่วยคลายความสงสัยนั้นลงได้บ้าง (การเลือกหัวข้อวิจัยมีความเสี่ยงสูงมาก ควรปรึกษาอาจารย์ที่ปรึกษาก่อนตัดสินใจ).

ดัดแปลงจาก https://cs224d.stanford.edu/notebooks/vanishing_grad_example.html (ข้อมูลเมื่อ 24 พ.ค. 2560).↩︎
ตัวอย่างคำสั่งและโปรแกรมต่าง ๆ ที่จะแสดงนี้ ทดสอบกับ ไพทอร์ช เวอร์ชั่น 1.0.0.↩︎
การรับมรดก (inheritance) เป็นกลไกการเขียนโปรแกรมเชิงวัตถุ (object-oriented programming) ที่สำคัญ ช่วยให้เราสามารถใช้โปรแกรมเดิมซ้ำได้ โดยเปลี่ยนเฉพาะส่วนที่จำเป็น.↩︎
เพื่อลดความซับซ้อนของโปรแกรม สำหรับชั้นซ่อน คลาส tANN1 รับฟังก์ชันกระตุ้น trelu ได้เท่านั้น.↩︎
ลำดับชั้นของความคิด เป็นแนวคิดทางวิศวกรรมคอมพิวเตอร์ และวิศวกรรมทั่วไป (และจริง ๆ แล้วก็รวมถึงกิจกรรมต่าง ๆ ไปจนถึงอารยธรรมของมนุษยชาติ) ที่จะมองหรือแก้ปัญหาในหลาย ๆ ระดับของรายละเอียด โดยการคิดในระดับบน จะละการพิจารณารายละเอียดของระดับล่างที่เกินความจำเป็นออก. การละรายละเอียดระดับล่างออก ช่วยลดภาระเชิงปัญญา ทำให้สามารถมองปัญหาไปได้ไกลขึ้น กว้างขึ้น และเป็นองค์รวมมากขึ้น.↩︎
ตัวแปรวนซ้ำ (iterable variable) หมายถึง ตัวแปรวัตถุ ที่สามารถให้ค่าสมาชิกของมันออกมาได้ทีละตัว ซึ่งสามารถใช้งานได้สะดวกกับการวนซ้ำด้วยคำสั่ง for. ไพธอน มีข้อมูลหลายชนิดที่เป็นตัวแปรวนซ้ำ เช่น ลิสต์ ทูเพิล และดิกชันนารี.↩︎
นั่นคือ เมื่อตรวจดูสัดส่วน เช่น รันคำสั่ง labels[:,0].shape แล้วจะเห็นสัดส่วนเป็น torch.Size([50]) ไม่ใช่ torch.Size([50, 1]) ที่หมายถึง ไพทอร์ชเทนเซอร์ สองลำดับชั้น.↩︎
โปรแกรม optim.SGD หมายถึง วิธีลงเกรเดียนต์แบบสโทแคสติก (stochastic gradient descent method) ซึ่งมีกลไกหลัก คือ วิธีลงเกรเดียนต์ และเน้นการสุ่มลำดับข้อมูล (ดูหัวข้อ [sec: minibatch]) นอกจากนั้น optim.SGD ยังมีกลไกโมเมนตัมด้วย (หัวข้อ [sec: momentum]).↩︎
เนื้อหา ในแบบฝึกหัดนี้ได้รับอิทธิพลหลัก ๆ จากกูดเฟโลและคณะ.↩︎
เพื่อให้เนื้อหามีความทั่วไป และไม่เยิ่นเย้อมาก ในที่นี้จะใช้คำว่า ความน่าจะเป็น ในความหมายของความน่าจะเป็น หรือในกรณีที่ตัวแปรที่เกี่ยวข้องเป็นตัวแปรสุ่มต่อเนื่อง จะหมายถึง ความหนาแน่นความน่าจะเป็น. ดูหัวข้อ [sec: continuous random variable] เพิ่มเติม สำหรับความต่างระหว่างความน่าจะเป็น และความหนาแน่นความน่าจะเป็น.↩︎
เนื่องจาก $p_0$ และ $p_1$ ไม่ได้เปรียบเทียบกับรหัสหนึ่งร้อน การใช้ซอฟต์แมกซ์ อาจเพิ่มการคำนวณโดยไม่จำเป็น และอาจส่งผลเสียต่อเสถียรภาพและคุณภาพของฝึกอีกด้วย. กรณีนี้ การทำนอร์มอไลซ์ให้เหมาะสม อาจจะเป็นทางเลือกที่ดีกว่า.↩︎
หลังจากฝึกไป $4000$ สมัยฝึก โดยเริ่มต้นค่าน้ำหนัก ด้วยวิธีกำหนดค่าน้ำหนักเซเวียร์ ด้วยอัตรา $\sqrt{2}$ โดยการฝึก $2500$ สมัยแรก ฝึกกับข้อมูลที่ $\sigma_0 = \sigma_1 = 0.5$ และ $1500$ สมัยต่อมา จึงฝึกกับข้อมูลที่มีค่า $\sigma_0$ และ $\sigma_1$ ดังกำหนด. การฝึกกับข้อมูลดังกำหนด ตั้งแต่แรก พบว่าให้ผลไม่ต่างกันอย่างมีนัยสำคัญ.↩︎
nn.Module จะเป็นคลาสแม่ของคลาสโครงข่ายประสาทเทียมที่เราสร้างขึ้น ดังนั้น ตัวแปรวัตถุของคลาสโครงข่ายประสาทเทียมที่เราสร้างขึ้น จึงสามารถใช้เมท็อดต่าง ๆ ของคลาส nn.Module ได้.↩︎
ดัดแปลงจาก .↩︎