4 การเรียนรู้ของเครื่องในโลกกว้าง
“Failure is the key to success;
each mistake teaches us something.”—Morihei Ueshiba
“ความล้มเหลวเป็นกุญแจสู่ความสำเร็จ
แต่ละความผิดพลาดสอนเราบางอย่าง.”—โมเรเฮอิ อุเรชิบะ
บทนี้ นำเสนอตัวอย่างการนำวิธีการเรียนรู้ของเครื่อง ไปประยุกต์ใช้กับงานการรู้จำรูปแบบ รวมถึง วิธีการเรียนรู้ของเครื่องแบบต่าง ๆ ที่หลากหลาย. หัวข้อ 1.1 นำเสนอตัวอย่างระบบวิเคราะห์พฤติกรรมลูกค้า ที่ใช้แบบจำลองการเรียนรู้ของเครื่องประกอบอยู่ในระบบ ทั้งในส่วนการตรวจจับตำแหน่งลูกค้า และการแสดงผล. หัวข้อ 1.1 อภิปราย เทคนิคหลาย ๆ อย่างที่ใช้ประกอบกับวิธีการเรียนรู้ของเครื่อง เพื่อสามารถใช้กับงานการรู้จำรูปแบบได้อย่างมีประสิทธิผล. หัวข้อ 1.2 อภิปราย ซัพพอร์ตเวกเตอร์แมชชีน ซึ่งเป็นหนึ่งในวิธีการเรียนรู้ของเครื่องอีกที่ได้รับความนิยมอย่างมาก. ซัพพอร์ตเวกเตอร์แมชชีน ออกแบบและพัฒนาโดยอาศัยศาสตร์การหาค่าดีที่สุด มีทฤษฎีรองรับมั่นคง และมีเบื้องหลังการออกแบบที่สละสลวย.
4.1 การวิเคราะห์พฤติกรรมลูกค้า
เนื้อหาในหัวข้อนี้ ได้รับอิทธิพลหลัก ๆ จากโครงการวิจัยการวิเคราะหพฤติกรรมลูกคาผานขอมูลวิดีโอจากกลองวงจรปด.
4.1.1 การวิเคราะห์พฤติกรรมลูกค้าจากภาพวิดีโอ
ขอมูลวิดีโอจากกลองวงจรปดในรานคาปลีก นอกจากใชเพื่อเหตุผลดานความปลอดภัยแลว ขอมูลวิดีโอยังสามารถนำมาใช เพื่อการวิเคราะหพฤติกรรมการจับจายของลูกคาที่เขามาภายในรานได. การเขาใจพฤติกรรมของลูกคาสามารถนำมาชวยเพิ่มโอกาสทางธุรกิจได เชน ความเขาใจบริเวณและเวลาที่ลูกคาใชขณะเขามาภายในราน สามารถใช้ประกอบการตัดสินใจ สำหรับการจัดวางสินคา หรือการจัดกิจกรรมสงเสริมการตลาดได้.
ระบบวิเคราะหพฤติกรรมอัตโนมัติจะชวยอำนวยความสะดวกในการวิเคราะหเบื้องตน ถึงพฤติกรรมของลูกคาที่เข้ามาในร้าน โดยใช้ขอมูลวิดีโอที่ถายจากกลองวงจรปด. ระบบตัวอย่างนี้ วิเคราะหพฤติกรรม ซึ่งคือ การตรวจหาตำแหน่งของลูกค้า เมื่อลูกค้าเข้ามาใช้บริการภายในร้านค้า และนำเสนอผลสรุป เป็นแผ่นภาพสรุป. แผ่นภาพสรุปที่ได้ สามารถนำไปช่วยประกอบการตัดสินใจด้านการตลาด และอาจช่วยให้เข้าใจรูปแบบการเข้าใช้พื้นที่ในบริเวณร้านได้ดีขึ้น.
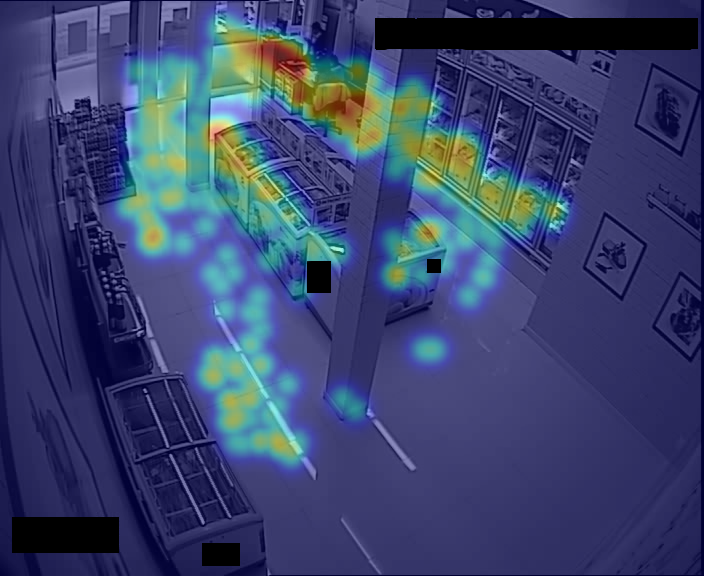
ขอมูลจากกลองวงจรปดภายในรานคาปลีก ถูกนำมาใช้เพื่อประมวลผล และตรวจหาตำแหนงของลูกคา แล้วจัดทำแผนภาพสรุป. รูป 1.1 แสดงตัวอยาง ของรูปแบบภาพสรุป ที่จัดทำเป็นรูปแบบแผนที่ความรอน (heat map). ภาพสรุปแสดงบริเวณที่พบลูกคาบอยที่สุดดวยสีแดง และสีโทนที่เย็นลงสื่อถึงความถี่ที่พบลูกคาลดลง (ความถี่ต่ำที่สุด แทนดวยสีที่เย็นที่สุด คือ สีน้ำเงิน).
4.1.2 ขั้นตอนการทำงานของระบบวิเคราะห์พฤติกรรมลูกค้าจากภาพวิดีโอ
ตัวอย่างระบบวิเคราะหพฤติกรรมอัตโนมัตินี้ มีส่วนประกอบหลักสองส่วน ได้แก่ (1) ส่วนการตรวจหาและระบุตำแหนงของลูกคาจากขอมูลวิดีโอ และ (2) ส่วนนำเสนอผล ที่นำตำแหนงของลูกคาที่ตรวจหาไดมาสรุปและแสดงผลเปนแผนที่ความรอน.
4.1.3 ส่วนของการตรวจหาและระบุตำแหน่งของลูกค้า จากข้อมูลวิดีโอ
ลักษณะงานวิเคราะห์พฤติกรรมลูกค้า เป็นงานลักษณะออฟไลน์ (offline mode) หรือลักษณะการประมวลผลเป็นชุด (batch processing ที่ไม่ใช่ระบบเวลาจริง real-time processing). เช่นเดียวกับงานของเบเนนสันและคณะ ที่ศึกษาการตรวจหาและระบุตำแหน่งคนเดินเท้า ซึ่งเป็นงานในลักษณะใกล้เคียงกัน งานการตรวจหาและระบุตำแหน่งลูกค้านี้ ดำเนินการโดย การแปลงจากวิดีโอมาเป็นชุดลำดับของภาพ แล้วจึงใช้วิธีการประมวลผลภาพ เพื่อตรวจหาและระบุตำแหน่งของลูกค้า.
การระบุตำแหน่งลูกค้าอาจทำได้หลายวิธี เช่น (ก) แนวทางวิธีลบฉากพื้นหลัง และ (ข) แนวทางวิธีตรวจหาภาพวัตถุ.
4.1.3.1 แนวทางวิธีลบฉากพื้นหลัง
แนวทางวิธีลบฉากพื้นหลัง ไม่ได้ใช้เทคนิคใดจากศาสตร์การเรียนรู้ของเครื่อง แต่ใช้อาศัยเทคนิคการประมวลผลภาพ และอาศัยลักษณะเฉพาะของข้อมูล. จากการสังเกตลักษณะเฉพาะของข้อมูล พื้นหลังของภาพวิดีโอค่อนข้างคงที่ ส่วนใหญ่ สิ่งที่เคลื่อนที่ในภาพมักจะเป็นคน ที่รวมทั้งลูกค้าและพนักงาน. แนวทางวิธีลบฉากพื้นหลัง อาศัยลักษณะเฉพาะของข้อมูลนี้เข้ามาช่วย.
แนวทางวิธีลบฉากพื้นหลัง (Background Subtraction) แสดงดังรูปที่ [fig: classic Background Subtraction Pipeline] ซึ่งเป็นแผนภูมิลำดับกระบวนการ. ข้อมูลวิดีโอ (ภาพซ้ายล่าง) จะถูกแปลงเป็นเฟรมภาพ (ขั้นตอน 1.1). หลังจากนั้น นำแต่ละภาพที่ได้ไปลบออกจากภาพพื้นหลัง (background หรือภาพในบริเวณร้านที่ไม่มีลูกค้าอยู่) รวมถึงการปรับปรุงเพื่อขยายความต่างให้ชัดเจนขึ้น (ขั้นตอนที่ 1.2a – 1.2c). สุดท้าย ทำการค้นหาและระบุตำแหน่งลูกค้าในภาพ (ขั้นตอนที่ 1.3a – 1.3b).
ขั้นตอนที่ 1.1. การแปลงจากวิดีโอไฟล์เป็นภาพ มีกระบวนทางเทคนิคที่มีรายละเอียดมาก รวมไปถึงข้อกำหนดต่าง ๆ ตามมาตราฐานของชนิดข้อมูลวิดีโอ แต่ในทางปฏิบัติมีเครื่องมือที่ช่วยทำงานเหล่านี้ได้มากมาย หนึ่งในเครื่องมือที่นิยมใช้ ก็เช่น โอเพ่นซีวี (OpenCV1) ซึ่งเป็นไลบรารี่รหัสเปิด (open-source library) สำหรับงานด้านทัศนคอมพิวเตอร์ (Computer Vision). ขั้นตอนที่ 1.2 การปรับปรุงภาพ เพื่อให้ตำแหน่งของลูกค้าเด่นชัดขึ้น เพื่อช่วยให้การตรวจหาตำแหน่งของลูกค้าในขั้นตอนต่อไปทำได้ง่าย. ขั้นตอนย่อยในการปรับปรุงภาพนี้ ได้แก่ เทคนิควิธีลบพื้นหลัง ที่นำภาพพื้นหลังไปลบออกจากภาพที่ต้องการตรวจหาตำแหน่งลูกค้า. สิ่งที่ต่างจากพื้นหลังก็จะปรากฏเด่นขึ้น (1.2a และ 1.2b) และ เทคนิควิธีแยกส่วนโดยการกำหนดระดับค่าขีดแบ่ง (segmentation by thresholding) ก็สามารถนำมาใช้ เพื่อแยกฉากหน้า (ที่อาจเป็นลูกค้า) ออกจากฉากหลัง. เทคนิควิธีแยกส่วนโดยการกำหนดระดับค่าขีดแบ่ง คือการตั้งค่าระดับขีดแบ่งขึ้นมาหนึ่งค่า โดย หากค่าความเข้มของพิกเซลมากกว่าระดับนั้น ก็จะปรับเพิ่มค่าความเข้มของพิกเซลนั้นไปจนมีค่ามากที่สุด (สว่างเต็มที่) ไม่เช่นนั้นก็ปรับลดค่าลงเป็นศูนย์ (มืดเต็มที่). ดังนั้น ภาพจะถูกแยกเป็นส่วนสว่างและมืดอย่างชัดเจน. ขั้นตอน 1.3 เป็นการนำภาพที่ปรับปรุงความต่างระหว่างฉากหน้าและฉากหลัง ไปตรวจหาตำแหน่งของลูกค้า ซึ่งใช้เทคนิคการตรวจหาแบบหน้าต่างเลื่อน (sliding window detection). เทคนิคการตรวจหาแบบหน้าต่างเลื่อน เป็นหนึ่งในวิธีที่นิยมใช้สำหรับงานการตรวจหาภาพวัตถุ. เทคนิคการตรวจหาแบบหน้าต่างเลื่อน เป็นเทคนิคการเลือกส่วนภาพ โดยส่วนภาพ(ในขนาดที่พอเหมาะแก่การตรวจสอบว่าเป็นวัตถุที่ต้องการหรือไม่) จะถูกเลือกขึ้นมาจากภาพที่สงสัย. การเลือกจะเริ่มที่มุมด้านหนึ่งของภาพ และขยับเลือกไปเรื่อย ๆ จนครอบคลุมทั้งภาพ. ส่วนภาพขนาดเล็กที่ถูกเลือกออกมานั้นจะถูกตรวจสอบว่ามีวัตถุที่ค้นหาอยู่ในส่วนภาพนั้นหรือไม่ (ขั้นตอน 1.3a). เมื่อได้ผลการตรวจสอบส่วนภาพขนาดเล็กจากตำแหน่งต่าง ๆ แล้ว ส่วนภาพต่าง ๆ ที่ได้ผลการตรวจเป็นบวกที่มีตำแหน่งใกล้ ๆ กัน จะถูกรวมกันตามเกณฑ์การรวมที่กำหนด และตำแหน่งของการรวมนั้นจะถูกบันทึกเป็นตำแหน่งของลูกค้าทั้งตัว (ขั้นตอน 1.3b). เมื่อถึงขั้นตอนนี้ ระบบก็จะสามารถระบุได้แล้วว่า ลูกค้าอยู่ที่ตำแหน่งใดในภาพ.

4.1.3.2 แนวทางของวิธีตรวจหาวัตถุ
กลไกจริง ๆ ของวิธีการลบฉากหลัง คือ การตรวจหาตำแหน่งของวัตถุที่ต่างจากฉากหลัง ซึ่งสมมติฐานก็คือน่าจะเป็นลูกค้า. วิธีการลบฉากหลังมีข้อดีคือ สามารถทำได้ง่ายและรวดเร็ว (ในกรณีที่มีภาพฉากหลังแล้ว). แต่ข้อเสีย คือความสามารถดังกล่าวไม่สามารถขยายไปใช้ในการแยกวัตถุอื่นได้ เช่น ยากที่จะแยกคนกับรถเข็นออกจากกันได้ และไม่สามารถนำไปใช้ในกรณีที่ฉากหลังมีการเปลี่ยนแปลงสูงได้ เช่น ไม่สามารถนำไปใช้ตรวจจับภาพคนเดินถนน ที่ฉากหลังเป็นสภาพการจราจรได้ และก็ไม่สามารถใช้ในกรณีคนมีการขยับน้อย เช่น ในสวนที่มีคนนั่งอ่านหนังสือ ฝึกสมาธิ หรือนอนหลับอยู่.
อีกแนวทางหนึ่งที่สามารถทำได้ คือ แนวทางวิธีตรวจหาวัตถุ. การตรวจหาวัตถุ (object detection) เป็นภารกิจการหาตำแหน่งของวัตถุในภาพ หากในภาพมีวัตถุปรากฎอยู่. แนวทางของวิธีตรวจหาวัตถุมีพื้นฐานมาจากสมมติฐานทางสถิติ เช่น รูปทรงของคนแม้จะมีความหลากหลาย แต่ก็มีรูปแบบและลักษณะร่วมกันอยู่มาก และวิธีการคือ การหาลักษณะร่วมเหล่านั้นออกมา และใช้มันช่วยในการจำแนกระหว่างคนกับสิ่งอื่น ๆ ที่ไม่ใช่คน. รูปที่ 1.3 แสดงขั้นตอนย่อย ๆ ในการตรวจหาตำแหน่งของลูกค้าด้วยวิธีการตรวจหาวัตถุ โดยเริ่มตั้งแต่
การแปลงข้อมูลวิดีโอออกมาเป็นข้อมูลภาพหลาย ๆ ภาพ (frame capture) เทียบเท่าขั้นตอน 1.1 ของรูปที่ 1.2 ของแนวทางการลบฉากหลัง. นั่นคือ การปรับปัญหาจากการทำงานกับข้อมูลวิดีโอ เป็นปัญหาเสมือนที่ทำงานกับภาพแทน.
การย่อและขยายภาพให้อยู่ในหลาย ๆ ขนาด (scaling) เพื่อให้วัตถุที่อยู่ห่างกล้องในระยะต่าง ๆ มีโอกาสที่จะถูกตรวจพบใกล้เคียงกัน.
การเลือกส่วนภาพ (window sampling). แนวทางนี้ ก็ยังคงเลือกใช้เทคนิคหน้าต่างเลื่อน. นั่นคือ ตีกรอบปัญหาการตรวจจับภาพวัตถุ เป็นปัญหาการจำแนกค่าทวิภาค โดยใช้การเลือกส่วนภาพออกมา เพื่อเป็นอินพุตของแบบจำลองจำแนก (ในขั้นตอนต่อไป).
การจำแนกส่วนภาพว่ามีภาพคนอยู่หรือไม่ (window classification). ภาพขนาดเท่า ๆ กัน (ได้จากการสุ่มภาพด้วยวิธีหน้าต่างเลื่อน) จะถูกผ่านเข้าแบบจำลองจำแนกข้อมูล โดยแบบจำลองจะทำหน้าที่ทำนายว่าภาพอินพุตนั้น มีภาพของวัตถุที่ต้องการ (ในที่นี้คือ ภาพคน) หรือไม่.
การลดผลการตรวจหาที่ซ้ำซ้อน (redundancy removal). การสุ่มด้วยวิธีหน้าต่างเลื่อน มักทำในลักษณะที่มีการซ้อนทับกัน เพื่อปัองกันการตัดกรอบที่กลางวัตถุ แต่การสุ่มในลักษณะนี้ก็อาจทำให้ การสุ่มในตำแหน่งใกล้เคียงกัน ตรวจพบวัตถุเดียวกันได้. ดังนั้น หลังการตรวจพบวัตถุแล้ว จึงต้องมีการทำการลดการซ้ำซ้อนลง. หลังจากขั้นตอนการลดการซ้ำซ้อน เราจะสามารถระบุตำแหน่งของวัตถุที่ตรวจพบได้.

จากนั้น ผลการตรวจหาที่ได้จะนำไปสรุป และแสดงผลด้วยวิธีแผนที่ความร้อน (hot zone analysis ซึ่งเป็นขั้นตอนที่ 6 ในรูป 1.3). ขั้นตอนที่ 2 ถึง 5 คือขั้นตอนที่ต่างจากแนวทางวิธีลบฉากหลัง (เปรียบเทียบกับ 1.2a ถึง 1.3b ในรูปที่ 1.2) ถึงแม้ทั้งสองแนวทางจะใช้กลไกของการเลือกส่วนภาพด้วยวิธีหน้าต่างเลื่อนก็ตาม.
4.1.3.2.1 การทำเทคนิคหน้าต่างเลื่อน.
วิธีหน้าต่างเลื่อน เป็นวิธีการเลือกส่วนภาพขนาดที่กำหนดจากข้อมูลภาพใหญ่ โดย การเลือกส่วนภาพจะเลือกทั่วถึงจากทุกบริเวณในภาพใหญ่ โดยอาจเริ่มจากมุมซ้ายบนของภาพใหญ่ เลือกส่วนภาพออกมา แล้วขยับไปทางขวา และทำเช่นนี้ไปจนสุดปลายด้านขวา แล้วจึงขยับลงล่างและไปเริ่มจากซ้ายสุด และทำลักษณะเช่นนี้อีก จนครอบคลุมบริเวณทั้งภาพใหญ่. ลำดับของภาพที่เลือกออกมา จะดูคล้ายกับลำดับของภาพที่มองจากหน้าต่างที่เลื่อนไปตำแหน่งต่าง ๆ ของภาพใหญ่ ดังนั้นเทคนิคนี้จึงเรียกว่า เทคนิคหน้าต่างเลื่อน. ขนาดของหน้าต่าง (window size) ซึ่งคือขนาดของส่วนภาพที่เลือก และขนาดของการขยับหน้าต่าง ที่มักเรียกว่า ขนาดขยับเลื่อน (stride) ซึ่งเป็นจำนวนพิกเซลของการขยับการเลือกส่วนภาพแต่ละครั้ง เป็นอภิมานพารามิเตอร์ของวิธีหน้าต่างเลื่อน.
รูป 1.4 แสดงตัวอย่างการทำงานของวิธีหน้าต่างเลื่อน. ในตัวอย่าง ภาพใหญ่ขนาด \(16\) พิกเซล กรอบหน้าต่างเลือกกว้าง \(8\) พิกเซล และขนาดขยับเลื่อนแนวนอนเป็น \(4\) พิกเซล ดังนั้นจึงสามารถขยับได้ \(3\) ตำแหน่งในแนวนอน (ได้แก่ เริ่มต้นที่พิกเซล 0, ขยับไปพิกเซล 4, และขยับไปพิกเซล 8). จำนวนตำแหน่งของหน้าต่างในแนวนอนและแนวตั้งสามารถเขียนเป็นการคำนวณทั่วไปได้ดังนี้ กำหนดให้เมทริกซ์ \(\boldsymbol{F} = [f_{m,n}]\), \(m = 0, \ldots, C-1\) และ \(n = 0, \ldots, R-1\) แทนภาพใหญ่ขนาด \(C \times R\) และ \(f_{m,n} \in \mathbb{I}\) เป็นค่าความเข้มของพิกเซลที่ตำแหน่ง \((m,n)\) และให้ \(\boldsymbol{W}_{ij} \in \mathbb{I}^{A \times B}\) แทนส่วนภาพขนาด \(A \times B\) ของดัชนีหน้าต่าง \((i,j)\). หากขนาดขยับเลื่อนตามแนวนอนและตั้งเป็น \((a,b)\) แล้ว วิธีหน้าต่างเลื่อน เป็นเสมือนฟังก์ชันแปลง \(S: \boldsymbol{F} \mapsto \{ \boldsymbol{W}_{ij} \}\) สำหรับดัชนี \(i = 0, \ldots, \lfloor \frac{C - A}{a} \rfloor\) และดัชนี \(j = 0, \ldots, \lfloor \frac{R - B}{b} \rfloor\). แต่ละส่วนภาพ \(\boldsymbol{W}_{ij} = [w_{p,q}(i,j)]\) เมื่อ \(p = 0, \ldots, A-1\) และ \(q = 0, \ldots, B-1\) เป็นเมทริกซ์ย่อย \(w_{p,q}(i,j) = f_{a \cdot i + p, b \cdot j + q}\).
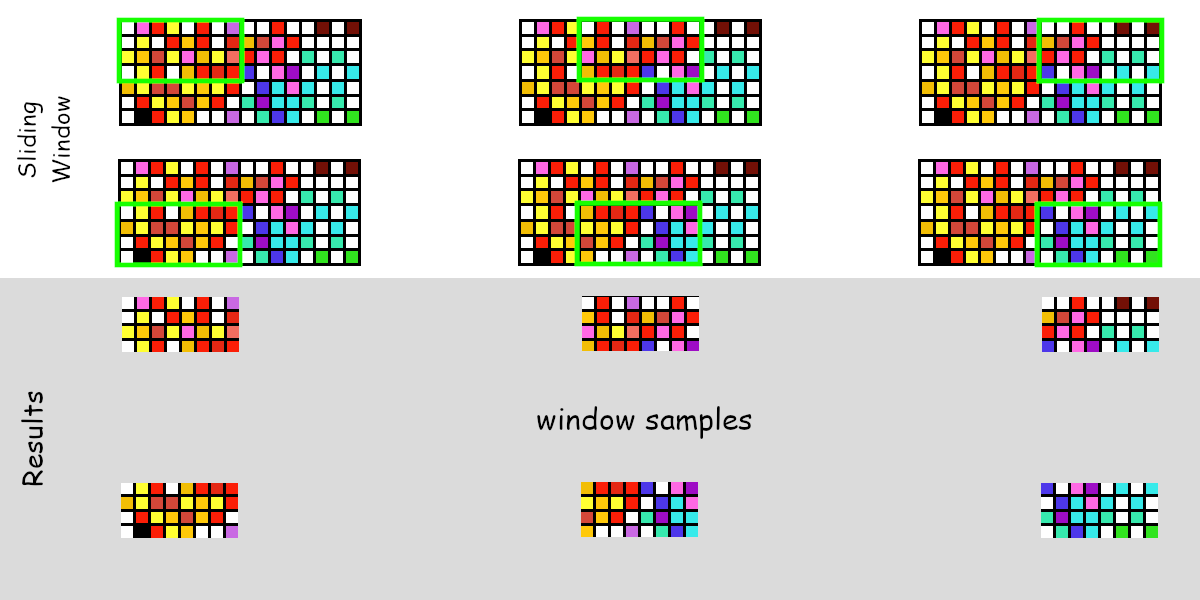
รูป 1.5 แสดงตัวอย่างการใช้วิธีหน้าต่างเลื่อนกับงานการตรวจจับภาพเป้าหมาย. ผลลัพธ์ที่ได้คือส่วนภาพต่าง ๆ. ส่วนภาพต่าง ๆ จะถูกนำไปตรวจสอบ ดัชนีของส่วนภาพที่พบว่ามีเป้าหมายอยู่ จะถูกนำไปใช้ระบุตำแหน่งของเป้าหมายในภาพใหญ่ (หากพบเป้าหมายในภาพ). จากอภิมานพารามิเตอร์ที่ใช้ (หน้าต่างขนาด \(128 \times 64\) ใช้ขนาดขยับเลื่อนเป็น \(16 \time 16\)) และขนาดของภาพใหญ่ (\(576 \times 704\)) หลังดำเนินการวิธีหน้าต่างเลื่อน จะได้ส่วนภาพ \(\boldsymbol{W}_{0,0}, \ldots, \boldsymbol{W}_{28, 40}\) (จาก \(\lfloor \frac{576 - 128}{16} \rfloor = 28\) และ \(\lfloor \frac{704 - 64}{16} \rfloor = 40\)). แต่ละส่วนภาพตัดมาจากภาพใหญ่ เช่น \[\boldsymbol{W}_{7,27} = \begin{bmatrix} f_{112,432} & \ldots & f_{112,495} \\ \vdots & \ddots & \vdots \\ f_{239,432} & \ldots & f_{239,495} \\ \end{bmatrix}\] เมื่อ \(f_{m,n}\) คือค่าความเข้มพิกเซลของภาพใหญ่ที่ตำแหน่งตามแนวตั้ง \(m\) และแนวนอน \(n\).
![ตัวอย่างการใช้วิธีหน้าต่างเลื่อนกับงานการตรวจจับภาพเป้าหมาย. ภาพซ้ายแถวบนสุด แสดงส่วนภาพแรก (W[0,0]) ที่วิธีหน้าต่างเลื่อนเริ่มต้น. และภาพขวาแถวล่างสุด แสดงส่วนภาพสุดท้าย (W[28,40]) ที่วิธีหน้าต่างเลื่อนเลือกออกมา เมื่อภาพใหญ่มีขนาด 576 \times 704 และหน้าต่างขนาด 128 \times 64 ใช้ขนาดขยับเลื่อนเป็น 16 \time 16.](04Classic/sliding_window_example.png)
4.1.3.2.2 การจำแนกและระบุตำแหน่งวัตถุ.
สำหรับแต่ละส่วนภาพที่เลือกมา \(\boldsymbol{W}_{ij}\) แบบจำลองจำแนกค่าทวิภาคสามารถใช้เพื่อทำนายว่าในส่วนภาพมีวัตถุเป้าหมายอยู่หรือไม่. นั่นคือ แบบจำลองจำแนกค่าทวิภาค เป็นเสมือนฟังก์ชันแปลง \(f: \boldsymbol{W}_{ij} \mapsto y_{ij}\) เมื่อ \(y_{ij}\) คือค่าทวิภาคที่ทำนาย ซึ่งในกรณีตัวอย่างนี้นิยามเป็น \(+1\) (มีเป้าหมายที่ค้นหาอยู่) หรือ \(-1\) (ไม่มีเป้าหมายที่ค้นหาอยู่). หาก \(y_{ij} = 1\) นั้นหมายถึง ส่วนภาพ \(\boldsymbol{W}_{ij}\) มีเป้าหมายอยู่ และตำแหน่งของเป้าหมาย ก็คือตำแหน่งต่าง ๆ ที่ \(\boldsymbol{W}_{ij}\) ครอบคลุม.
การแปลงจากส่วนภาพเป็นค่าทวิภาค ในตัวอย่างนี้ จะดำเนินเป็นสองขั้นตอน ได้แก่ (1) การแปลงส่วนภาพ ที่มักมีจำนวนมิติสูงมาก เป็นลักษณะสำคัญ ที่มีจำนวนมิติน้อยลงและเกี่ยวข้องการจำแนกเป้าหมายจากสิ่งอื่น ๆ และ (2) การแปลงลักษณะสำคัญที่ได้จากขั้นตอนแรกไปเป็นค่าทวิภาคที่ต้องการทำนาย. ลักษณะสำคัญ เป็นตัวแทนของอินพุตต้นฉบับในแบบที่ช่วยให้ภาระกิจเป้าหมายดำเนินการได้ง่ายขึ้น. การเทคนิคที่สำคัญต่าง ๆ ในงานการตรวจจับภาพวัตถุ ล้วนเกี่ยวข้องโดยตรงกับการทำลักษณะสำคัญแทนของอินพุตต้นฉบับ ไม่ว่าจะเป็น ลักษณะฮาร์ (Haar features) หรือ แผนภูมิแท่งของทิศทางเกรเดียนต์ (Histogram of Oriented Gradient) หรือ ถุงของทัศนะถ้อยคำ (Bag of Visual Words) เป็นต้น. ลักษณะสำคัญที่พัฒนาขึ้นมาในยุคหลัง ๆ อาจสร้างขึ้นจากลักษณะสำคัญที่พัฒนามาก่อนแล้ว เช่น แบบจำลองแปลงรูป (deformable model) ที่ใช้แผนภูมิแท่งของทิศทางเกรเดียนต์ เป็นพื้นฐาน. แม้แต่แนวทางการเรียนรู้เชิงลึก (บท [chapter: Deep Learning]) ที่โดยทั่วไปแล้ว ไม่จำเป็นต้องดำเนินการแปลงเป็นสองขึ้นตอน นั่นคือ ไม่ต้องเตรียมลักษณะสำคัญให้แบบจำลอง และสามารถรับอินพุตเป็นภาพต้นฉบับได้โดยตรง ก็มีการใช้ลักษณะสำคัญ เพียงแต่แบบจำลองทำการสร้างลักษณะสำคัญขึ้นได้เองจากข้อมูลจำนวนมากที่ใช้ฝึก.
ตัวอย่างนี้ดำเนินการจำแนกค่าทวิภาคของส่วนภาพโดย (1) ส่วนภาพ \(\boldsymbol{W}_{ij}\) จะถูกแปลงเป็นเวกเตอร์ลักษณะสำคัญ \(\boldsymbol{X}_{ij}\) และจากนั้น (2) ลักษณะสำคัญ \(\boldsymbol{X}_{ij}\) จะถูกแปลงเป็นฉลากทำนาย \(y_{ij} \in \{-1, +1\}\). ตัวอย่างนี้ แสดงการใช้แผนภูมิแท่งของทิศทางเกรเดียนต์ เป็นลักษณะสำคัญ และใช้ซัพพอร์ตเวกเตอร์แมชชีน เป็นแบบจำลองทำนาย.
หมายเหตุ แนวทางนี้ เพียงตรวจจับตำแหน่งของบุคคลในภาพ และไม่ได้มีการจำแนกแยกแยะมโนคติระดับสูง ว่าบุคคลในภาพเป็นลูกค้าจริง ๆ หรือเป็นพนักงานร้าน. เพื่อจะวิเคราะห์ในมโนคติระดับสูงดังกล่าว รูปแบบของเครื่องแบบ และเส้นทางการเคลื่อนที่ อาจนำมาใช้ประกอบได้.
4.1.3.2.3 การสกัดลักษณะสำคัญ.
แผนภูมิแท่งของทิศทางเกรเดียนต์ (Histogram of Oriented Gradients) ที่มักย่อเป็น เอชโอจี (HOG) เป็นลักษณะสำคัญที่นิยมใช้ในงานคอมพิวเตอร์วิทัศน์. เอชโอจี เป็นฟังก์ชันแปลง \(H: \boldsymbol{W} \mapsto \boldsymbol{x}\) เมื่อ \(\boldsymbol{W} \in \mathbb{I}^{A \times B}\) เป็นเมทริกซ์ของค่าความเข้มพิกเซล และ \(\boldsymbol{x} \in \mathbb{R}^D\) เป็นเวกเตอร์ค่าลักษณะสำคัญเอชโอจี. โดยทั่วไปแล้ว ขนาดของเวกเตอร์ \(\boldsymbol{x}\) จะเล็กกว่าขนาดของ \(\boldsymbol{W}\) มาก (นั่นคือ \(D << A \times B\)). สมมติฐานของเอชโอจี คือการแจกแจงพิกเซลเกรเดียนต์ของภาพสามารถเป็นนัยที่บ่งชี้รูปร่างและสามารถใช้ระบุเป้าหมายได้.
เอชโอจีเริ่มด้วยการคำนวณพิกเซลเกรเดียนต์ \(\boldsymbol{G}\). พิกเซลเกรเดียนต์ที่ตำแหน่ง \((r,c)\) เขียนด้วยสัญกรณ์ \(\boldsymbol{g}_{rc} =[g_x(r,c), g_y(r,c)]^T\) เมื่อ \(g_x(r,c) =f_{r,c+1} - f_{r,c}\) และ \(g_y(r,c) = f_{r+1,c} - f_{rc}\) และ \(f_{rc}\) คือค่าความเข้มพิกเซลของภาพที่ตำแหน่งแนวตั้ง \(r\) และแนวนอน \(c\) โดย กำหนดให้ \(f_{rc} \equiv 0\) เมื่อดัชนี \(r\) หรือ \(c\) เกินขอบเขตภาพ (\(r > R\) หรือ \(c > C\)). พิกเซลเกรเดียนต์ สามารถเขียนในรูปขนาดและมุมได้ ด้วยสัญกรณ์ \(\boldsymbol{g}_{rc} = m_{rc} \angle \theta_{rc}\) โดยขนาด \(m_{rc} = \sqrt{g_x^2(r,c) + g_y^2(r,c)}\) และมุม 2 \(\theta_{rc} = \arctan \frac{g_y(r,c)}{g_x(r,c)}\). รูป 1.6 แสดงค่าพิกเซลเกรเดียนต์ของส่วนภาพตัวอย่างที่มีเป้าหมาย และที่ไม่มีเป้าหมายอยู่.

จากนั้น เอชโอจีดำเนินการโดยแบ่งส่วนภาพ \(\boldsymbol{W}\) เป็นส่วนย่อย ๆ และเรียกแต่ละส่วนย่อยว่า เซลล์ (cell). ในแต่ละเซลล์ เอชโอจีจัดทำข้อมูล โดยจินตนาการเป็นเสมือนการทำแผนภูมิแท่ง โดย แต่ละแท่ง แทนค่าขนาดของเกรเดียนต์ในแต่ละทิศทาง (ทิศทางที่ใกล้เคียงกันจะถูกรวมอยู่ในแท่งเดียวกัน) และความสูงของแต่ละแท่ง เรียกว่า โหวต (vote) คำนวณจากผลรวมขนาดของเกรเดียนต์ในทิศทางของแท่งนั้น ๆ. ขึ้นตอนสุดท้าย เซลล์ต่าง ๆ ที่จะถูกรวมกันเป็นบล็อก (block) ในลักษณะซ้อนทับกัน และค่าโหวตจากเซลล์ในบล็อกจะถูกนอร์มอร์ไลซ์ภายในบล็อก. ค่าลักษณะสำคัญของเอชโอจี คือค่าโหวตที่ถูกนอร์มอร์ไลซ์แล้วจากบล็อกต่าง ๆ. นั่นคือ ขั้นตอนแรก คำนวณโหวตของเซลล์จากส่วนภาพ \(\boldsymbol{W}\) ที่มีขนาด \(A \times B\) โดยดำเนินการแปลง \(\boldsymbol{W} \mapsto \{\boldsymbol{v}_{ij}\}\) สำหรับดัชนีแนวตั้ง \(i = 0, \ldots, \lfloor \frac{A}{h_v} \rfloor - 1\) และดัชนีแนวนอน \(j = 0, \ldots, \lfloor \frac{B}{w_v} \rfloor - 1\) เมื่อ \(\boldsymbol{v}_{ij}\) เป็นเวกเตอร์ของเซลล์โหวต ที่เซลล์มีขนาด \(h_v \times w_v\).
หากเลือกจำนวนทิศทางของแผนภูมิแท่งเป็น \(K\) ทิศทาง เซลล์ \(\boldsymbol{v}_{ij} \in \mathbb{R}^K\) จะมีส่วนประกอบที่ \(k^{th}\) ของเซลล์ ที่เขียนเป็นสัญกรณ์ \(v_k(i,j)\) และสามารถคำนวณค่าได้จากผลรวมของขนาดของเกรเดียนต์ในทิศทางที่ \(k^{th}\) รวมถึงทิศทางใกล้เคียง ของพิกเซลที่อยู่ในขอบเขตของเซลล์. นั่นคือ หากส่วนภาพ \(\boldsymbol{W} = [w_{r,c}]\) โดย \(r = 0, \ldots, A-1\) และ \(c = 0, \ldots, B-1\) มีขนาดพิกเซลเกรเดียนต์ \(m_{rc}\) และมุมพิกเซลเกรเดียนต์ \(\theta_{rc}\) แล้วเซลล์โหวต \(v_k(i,j) = \sum_{r,c \in \Omega_{\mathrm{cell}}} m_{rc}\) สำหรับ \(k = 0, \ldots, K-1\) เมื่อเซต \(\Omega_{\mathrm{cell}}\) แทนเงื่อนไขพิกเซลในขอบเขตของเซลล์ ได้แก่ \(i \cdot h_v \leq r < (i+1) \cdot h_v\) และ \(j \cdot w_v \leq c < (j+1) \cdot w_v\) และเงื่อนไขทิศทาง ได้แก่ \(\frac{k \cdot 360}{K} \leq \theta_{rc} < \frac{(k+1) \cdot 360}{K}\).
รูป 1.9 แสดงตัวอย่างการแบ่งส่วนภาพออกเป็นเซลล์. จากอภิมานพารามิเตอร์ของตัวอย่าง ส่วนภาพถูกแบ่งออกเป็นเซลล์ \(\boldsymbol{v}_{0,0}, \ldots, \boldsymbol{v}_{15, 7}\) รวมทั้งหมด \(128\) เซลล์. ค่าขนาดของพิกเซลเกรเดียนต์ในเซลล์จะถูกนำมารวมกันตามทิศทาง. ในภาพแสดงตัวอย่างเมื่อเลือกทำ \(9\) ทิศทาง ดังนั้นผลลัพธ์คือหนึ่งเซลล์จะมีส่วนประกอบ \(9\) ตัวสำหรับทิศทาง \(0, 40, 80, 120, 160, 200, 240, 280, 320\) องศา. แต่ละทิศทางครอบคลุมทิศทางใกล้เคียง เช่น \(0\) องศา ครอบคลุม \(0 \leq \theta_{rc} < 40\). หมายเหตุ ภาพในรูป 1.9 มีการใช้ค่าชดเชย (offset) เพื่อใช้ทิศทางตัวแทนอยู่ตรงกลาง. นั่นคือใช้เงื่อนไขทิศทาง \(\frac{k \cdot 360}{K} + \delta \leq \theta_{rc} < \frac{(k+1) \cdot 360}{K} + \delta\) และใช้ค่าชดเชย \(\delta = -\frac{360}{2 K}\) ซึ่งในกรณีนี้คือ \(-20\). นั่นทำให้ \(0\) องศา ครอบคลุม \(-20 \leq \theta_{rc} < 20\).
 |
 |
 |
จากเซลล์โหวตที่ได้ เพื่อลดผลกระทบของแสงและเงาในบริเวณต่าง ๆ เซลล์จะถูกรวมเป็นบล็อก. นั่นคือ หากบล็อกมีขนาด \(n_y \times n_x\) เซลล์ และมีขนาดขยับเลื่อนบล็อกเป็น \(m_y \times m_x\) เซลล์ ส่วนภาพ \(\boldsymbol{W}\) ที่มีจำนวนเซลล์เป็น \(N_y \times N_x\) จะมีบล็อก \(\boldsymbol{b}_{pq}\) สำหรับ \(p = 0, \ldots, \lfloor \frac{N_y - n_y}{m_y} \rfloor\) และ \(q = 0, \ldots, \lfloor \frac{N_x - n_x}{m_x} \rfloor\). บล็อก \(\boldsymbol{b}_{pq}\) จะมีส่วนประกอบเป็นค่าเซลล์โหวตของเซลล์ในขอบเขตของบล็อก. นั่นคือ \(\boldsymbol{b}_{pq} = \{ \hat{\boldsymbol{v}}_{ij} \}_{i,j \in \Omega_{\mathrm{block}}}\) เมื่อเซต \(\Omega_{\mathrm{block}}\) แทนเงื่อนไข \(p \cdot m_y \leq i < p \cdot m_y + n_y\) และ \(q \cdot m_x \leq j < q \cdot m_x + n_x\). เวกเตอร์ \(\hat{\boldsymbol{v}}_{ij}\) คือค่าเซลล์โหวตหลังการทำนอร์มอร์ไลซ์ นั่นคือ ส่วนประกอบที่ \(k^{th}\) ของมัน \(\hat{v}_k(i,j) = (v_k(i,j) - v_{\min}(p,q))/(v_{\max}(p,q) - v_{\min}(p,q))\) โดย \(v_k(i,j)\) คือเซลล์โหวตที่ \(k^{th}\) ของเซลล์ \((i,j)\) และ \(v_{\max}(p,q)\) กับ \(v_{\min}(p,q)\) คือค่าเซลล์โหวตที่มากที่สุดกับน้อยที่สุดในบล็อก ตามลำดับ.
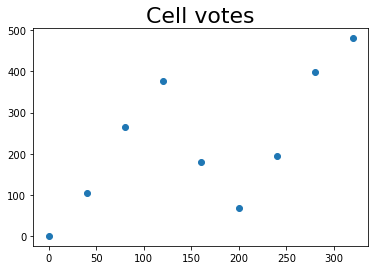
รูป 1.10 แสดงตัวอย่างขั้นตอนการทำบล็อก. ในตัวอย่าง บล็อกขนาด \(2 \times 2\) เซลล์ รวมผลโหวตของ \(4\) เซลล์ หรือเท่ากับ \(36\) ค่าโหวต. หากส่วนภาพมีจำนวนเซลล์เป็น \(16 \times 8\) เซลล์ จะมีจำนวนบล็อกทั้งหมดเป็น \(\left( \lfloor \frac{16 - 2}{1} \rfloor + 1 \right) \times \left( \lfloor \frac{8 - 2}{1} \rfloor + 1 \right)\) \(=105\) บล็อก. ดังนั้น สำหรับส่วนภาพขนาด \(128 \times 64\) ใช้เซลล์ขนาด \(8 \times 8\) ทำโหวต \(9\) ทิศทาง ใช้บล็อกขนาด \(2 \times 2\) และขนาดขยับเลื่อน \(1 \times 1\) ลักษณะสำคัญของเอชโอจี จะมี \(105 \times 2 \times 2 \times 9 = 3780\) ค่า.
![ขั้นตอนการทำเอชโอจีบล็อก. บล็อกขนาด 2 \times 2 เซลล์ และใช้ขนาดขยับเลื่อน 1 \times 1 เซลล์. แต่ละเซลล์ทำโหวต 9 ทิศทาง. ภาพซ้าย แสดงส่วนภาพ โดยเส้นสีเขียวแสดงขอบเขตแบ่งเซลล์ \boldsymbol{v}_{0,0} ถึง \boldsymbol{v}_{1,2} และเส้นสีแดงแสดงขอบเขตของบล็อก \boldsymbol{b}_{0,1}. ภาพถัดมา (ชื่อภาพ Cell[0,0] ถึง Cell[1,2]) แสดงค่าเซลล์โหวตของเซลล์ \boldsymbol{v}_{0,0} ถึง \boldsymbol{v}_{1,2}. ภาพขวาบน แสดงเซลล์โหวตภายในบล็อกก่อนทำนอร์มอร์ไลซ์. ภาพขวาล่าง ค่าของบล็อก.](04Classic/hog_block01.png)
รูป 1.12 แสดงตัวอย่างของลักษณะสำคัญของเอชโอจี สำหรับส่วนภาพที่มีเป้าหมาย และส่วนภาพที่ไม่มีเป้าหมาย. ลักษณะสำคัญที่แปลงมาอาจจะดูยากด้วยตาเปล่า. การวัดผลที่เหมาะสมจึงมีความสำคัญมาก.


ข้อสังเกต การตรวจจับภาพวัตถุ ที่ใช้วิธีการหน้าต่างเลื่อนกับลักษณะสำคัญเอชโอจี มีการทำงานในลักษณะพื้นที่ย่อย. นั่นคือ หน้าต่างและขนาดขยับเลื่อน ในวิธีหน้าต่างเลื่อน แบ่งจากภาพใหญ่เป็นส่วนภาพ. เซลล์ ในเอชโอจี แบ่งจากส่วนภาพเป็นเซลล์ แล้วใช้บล็อกกับขนาดขยับเลื่อนบล็อก แบ่งจากส่วนภาพเป็นบล็อก โดยอาศัยค่าที่ได้จากเซลล์. ทั้งสามระดับมีการทำงานในลักษณะคล้าย ๆ กัน ขั้นตอนหนึ่งต่อจากอีกขั้นตอนหนึ่ง. บทที่ [chapter: Deep Learning] อภิปรายแนวคิดของการเรียนรู้เชิงลึก และโครงสร้างคอนโวลูชั่น ที่ทำแนวคิดในลักษณะนี้ แต่ทำในลักษณะที่ทั่วไปและยืดหยุ่นขึ้น. ปัจจุบัน การเรียนรู้เชิงลึกและโครงสร้างคอนโวลูชั่น เป็นศาสตร์และศิลป์ของการตรวจจับภาพวัตถุ และสามารถให้ผลการทำงานที่แม่นยำมาก.
4.1.3.2.4 การจำแนกค่าทวิภาค.
จากภาพ \(\boldsymbol{F}\) เลือกส่วนภาพต่าง ๆ \(\boldsymbol{W}_{ij}\) ออกมาด้วยวิธีหน้าต่างเลื่อน. แต่ละส่วนภาพ \(\boldsymbol{W}_{ij}\) จะถูกสกัดเป็นลักษณะสำคัญ \(\boldsymbol{x}_{ij}\). ตอนนี้จากลักษณะสำคัญ \(\boldsymbol{x}_{ij}\) แบบจำลองจำแนกค่าทวิภาคสามารถนำมาใช้เพื่อทำนายผลว่าที่ตำแหน่ง \((i,j)\) มีเป้าหมายอยู่หรือไม่. แบบจำลองจำแนกค่าทวิภาค มีหลายชนิด. บทที่ [chapter: ANN] อภิปรายโครงข่ายประสาทเทียม. โครงข่ายประสาทเทียม ก็สามารถนำมาใช้ได้ แต่ตัวอย่างนี้ นำเสนอแบบจำลองจำแนกค่าทวิภาค อีกชนิดที่ได้รับความนิยมมาก คือ ซัพพอร์ตเวกเตอร์แมชชีน.
แบบจำลองจำแนกค่า (ทั้งการจำแนกค่าทวิภาค และการจำแนกกลุ่ม) มีหลายชนิด และอาจแบ่งเป็นแนวทางใหญ่ ๆ ได้สามแนวทาง. แนวทางแรก เรียกว่า แนวทางแบบจำลองแบ่งแยก (discriminative model). แนวทางนี้ เริ่มจากการสร้างแบบจำลองแบ่งแยก ที่ทำนายความน่าจะเป็นแบบมีเงื่อนไข ที่เอาต์พุตจะเป็นหนึ่ง สำหรับอินพุตที่ถาม นั่นคือ \(\mathrm{Pr}(y=1|\boldsymbol{x})\) หรือสำหรับการจำแนกกลุ่ม ความน่าจะเป็นแบบมีเงื่อนไขของเอาต์พุตกลุ่มที่ \(k^{th}\) สำหรับอินพุตที่ถาม นั่นคือ \(\mathrm{Pr}(y=k|\boldsymbol{x})\). หลังจากนั้น ใช้ทฤษฎีการตัดสินใจ เช่น วิธีระดับค่าขีดแบ่ง เพื่อเลือกค่าทวิภาพ หรือฉลากของกลุ่ม สำหรับกรณีการจำแนกกลุ่ม. โครงข่ายประสาทเทียม (บท [chapter: ANN]) สำหรับการจำแนกค่าทวิภาค หรือสำหรับการจำแนกกลุ่ม ก็จัดเป็นแบบจำลองแบ่งแยก. อย่างไรก็ตาม การตีความเอาต์พุตของโครงข่ายประสาทเทียมในเชิงความน่าจะเป็น โดยเฉพาะกรณีจำแนกกลุ่มว่า \(\hat{y}_k \approx \mathrm{Pr}(y=k|\boldsymbol{x})\) มีข้อสังเกต ข้อสงสัย และประเด็นที่กำลังสำรวจและศึกษาวิจัยอยู่.
แนวทางที่สอง เรียกว่า แนวทางแบบจำลองสร้างกำเนิด (generative model). แนวทางนี้ อาศัยความน่าจะเป็นแบบมีเงื่อนไขของอินพุต สำหรับเอาต์พุตแต่ละแบบ นั่นคือ \(\mathrm{Pr}(\boldsymbol{x}|y)\) และความน่าจะเป็นก่อนของเอาต์พุตแต่ละแบบ นั่นคือ \(\mathrm{Pr}(y)\) เพื่ออนุมานความน่าจะเป็นภายหลัง จากกฎของเบส์. นั่นคือ \[\begin{eqnarray} \mathrm{Pr}(y=k|\boldsymbol{x}) = \frac{\mathrm{Pr}(\boldsymbol{x}|y=k) \cdot \mathrm{Pr}(y=k)}{\mathrm{Pr}(\boldsymbol{x})} \label{eq: generative model} \end{eqnarray}\] โดย \(\mathrm{Pr}(\boldsymbol{x}) = \sum_k \mathrm{Pr}(\boldsymbol{x}|y=k) \cdot \mathrm{Pr}(y=k)\). หมายเหตุ บางแบบจำลอง แม้อาศัยการอนุมานการแจกแจงของอินพุต แต่อาจไม่ได้ประมาณ \(\mathrm{Pr}(\boldsymbol{x}|y)\) ออกมาโดยตรง เช่น โครงข่ายปรปักษ์เชิงสร้างกำเนิด (Generative Adversarial Network คำย่อ GAN) หรือ ตัวเข้าอัตรหัส (Autoencoder).
แนวทางที่สาม เป็นการสร้างฟังก์ชันที่แปลงอินพุตไปเป็นเอาต์พุตโดยตรง นั่นคือ \(f: \boldsymbol{x} \mapsto y\) โดยไม่ได้อาศัยความน่าจะเป็น หรือไม่สามารถตีในเชิงความเป็นความน่าจะเป็น. แนวทางนี้ เรียกว่า แนวทางฟังก์ชันแบ่งแยก (discriminant function). ซัพพอร์ตเวกเตอร์แมชชีน ก็จัดอยู่ในแนวทางนี้. หัวข้อ 1.2 อภิปรายซัพพอร์ตเวกเตอร์แมชชีน และทฤษฎีเบื้องหลัง.
4.1.4 การกำจัดการระบุซ้ำซ้อน
หลังจากขั้นตอนการจำแนกส่วนภาพที่มีเป้าหมายแล้ว ตำแหน่งของส่วนภาพที่ถูกจำแนกว่ามีเป้าหมาย จะถูกบันทึกเป็นค่าตำแหน่งที่ตรวจพบ. ตำแหน่ง อาจบันทึกเป็นพิกัดของกล่องขอบเขต (bounding box) เช่น พิกัด \((x,y)\) มุมขวาบนของกล่องขอบเขต กับพิกัดมุมล่างซ้าย หรืออาจจะเป็น พิกัดมุมขวาบนกับความกว้างและความสูง. กล่องขอบเขต สามารถนิยามเป็นขอบเขตของหน้าต่างที่เลือกส่วนภาพออกมา. ส่วนภาพในบริเวณใกล้เคียงกัน อาจถูกระบุว่ามีเป้าหมาย โดยที่เป้าหมายที่ส่วนภาพเหล่านั้นมี เป็นเป้าหมายเดียวกัน ซึ่งเป็นการระบุซ้ำซ้อน. รูป 1.5 แสดงตัวอย่างส่วนภาพ ที่ได้จากวิธีหน้าต่างเลื่อน. สังเกตว่า มีหลายส่วนภาพที่ครอบคลุมเป้าหมายเดียวกัน และอาจมีการระบุซ้ำซ้อนเกิดขึ้น.
จากตำแหน่งของส่วนภาพต่าง ๆ ที่ซ้ำซ้อน จะมีแค่ตำแหน่งเดียวที่จะเป็นตัวแทนของตำแหน่งของเป้าหมาย และที่เหลือจะถูกลบทิ้งไป. ขั้นตอนการกำจัดการระบุซ้ำซ้อนนี้ จะเรียกว่า การกำจัดความซ้ำซ้อน (redundancy removal). การกำจัดความซ้ำซ้อน ดำเนินการตั้งแต่ตรวจสอบความซ้ำซ้อน และกำจัดความซ้ำซ้อนที่พบ. ผลลัพธ์คือ ตำแหน่งต่าง ๆ ของการตรวจจับ ที่ไม่ซ้ำซ้อนกัน.
เพื่อตรวจสอบความซ้ำซ้อน แนวทางที่นิยม คือ กำหนดค่าระดับขีดแบ่ง \(\tau\) และกล่องขอบเขตสองกล่อง จะถือว่าซ้ำซ้อนกัน เมื่อ บริเวณซ้อนทับกันมีค่าการซ้อนทับมากกว่า ค่าระดับขีดแบ่ง \(\tau\). ค่าการซ้อนทับ มักถูกวัดด้วย ไอโอยู (IoU ซึ่งย่อมาจาก Intersect over Union) ซึ่งเป็นสัดส่วนพื้นที่ซ้อนทับกันต่อพื้นที่รวม. นั่นคือ \[\begin{eqnarray} \mathrm{IoU} = \frac{A_1 \cap A_2}{A_1 \cup A_2} \label{eq: IoU} \end{eqnarray}\] เมื่อ \(A_1\) และ \(A_2\) คือพื้นที่ของกล่องขอบเขตสองกล่องที่พิจารณา.
สำหรับกล่องขอบเขตต่าง ๆ ที่ซ้ำซ้อนกัน การกำจัดความซ้ำซ้อน อาจทำโดยสุ่มเลือกกล่องขอบเขตไว้กล่องหนึ่ง และตัดกล่องที่เหลือทิ้งก็ได้ แต่อาจทำให้คุณภาพโดยรวมของการตรวจจับด้อยลง. วิธีการระงับค่าไม่มากสุดท้องถิ่น (non-local-maximum suppression) จะระงับหรือตัดทิ้งกล่องขอบเขต ที่มีค่าความเหมาะสมไม่มากที่สุด เมื่อเปรียบเทียบกับกล่องขอบเขตอื่น ๆ ที่อยู่รอบ ๆ กล่องนั้น. ค่าความเหมาะสมของกล่องขอบเขต อาจได้มาจากแบบจำลองจำแนก เช่น กรณีโครงข่ายประสาทเทียม ค่าเอาต์พุตของโครงข่าย (ก่อนผ่านการตัดสินใจด้วยวิธีระดับค่าขีดแบ่ง) ถูกตีความเป็นค่าความน่าจะเป็น และสามารถนำมาใช้เป็นค่าความเหมาะสมได้. สำหรับกรณีซัพพอร์ตเวกเตอร์แมชชีน ค่าคะแนนตัดสินใจ (decision score สมการ \(\eqref{eq: svm discriminant function support vectors}\)) สามารถนำมาใช้ได้. อาณาเขตรอบกล่องที่พิจารณา โดยทั่วไป มักหมายถึงกล่องที่อยู่ติดกัน แต่อย่างไรก็ตาม ความกว้างของอาณาเขตนี้ สามารถกำหนดเป็นอภิมานพารามิเตอร์ได้.
4.1.5 การนำเสนอผลด้วยแผนที่ความร้อน
แผนที่ความร้อน เป็นแผนภาพสี ที่ให้ข้อมูลความถี่เชิงพื้นที่. ความถี่ของตำแหน่งที่พบลูกค้าบ่อย ๆ อนุมานมาจากพิกัดตำแหน่งต่าง ๆ ที่ตรวจพบลูกค้า จากชุดลำดับภาพของวิดีโอ. เวลาที่ลูกค้าใช้ในแต่ละตำแหน่ง จะสะท้อนออกมาในความถี่ที่แสดงนี้.
จากพิกัดตำแหน่งที่ตรวจพบลูกค้า ซึ่งอาจเป็นพิกัดของกล่องขอบเขต จะถูกแปลงเป็นพิกัดตัวแทน ซึ่งอาจใช้จุดศูนย์กลางของกล่องขอบเขต. จากนั้น พิกัดตำแหน่งที่ตรวจพบลูกค้าในแต่ละภาพจะถูกนำมารวมกัน ซึ่งเขียนเป็น \(\boldsymbol{D} = \{\boldsymbol{d}_i\}\) สำหรับ \(i=1,\ldots, N\) เมื่อ \(\boldsymbol{d}_i = [x_i, y_i]^T\) เป็นพิกัดตำแหน่งที่พบลูกค้า ในแนวนอนและแนวตั้งของภาพ ตามลำดับ. ดัชนี \(i\) เป็นดัชนีของพิกัด และ \(N\) คือจำนวนพิกัดทั้งหมดที่ต้องการนำมาสรุปเป็นความถี่เชิงพื้นที่. หมายเหตุ ในทางปฏิบัติ การเลือกพิกัดตรวจพบมาสรุปนั้น อาจเลือกตามระยะเวลา เช่นภายในหนึ่งเดือนที่ผ่านมา หรือ อาจเลือกตามช่วงเวลาที่สนใจได้ เช่นแยกสรุประหว่างวันธรรมดา และวันเสาร์อาทิตย์. แต่ ณ ที่นี้ แสดงดัชนี \(i\) เป็นดัชนีสำหรับพิกัดที่คัดเลือกมาแล้ว และ \(N\) เป็นจำนวนทั้งหมดที่ต้องการนำมาสรุปรวมกัน.
การสร้างแผนที่ความร้อน ก็คือ การแปลงข้อมูล \(\{\boldsymbol{d}_i\}\) ไปเป็นภาพสีขนาด \(H \times W\). วิธีหนึ่งที่นิยมคือ วิธีการประมาณความหนาแน่นแก่น (Kernel Density Estimation คำย่อ KDE). วิธีการประมาณความหนาแน่นแก่น เป็นการคำนวณการแจกแจงความน่าจะเป็นของข้อมูล และจัดเป็นแบบจำลองสร้างกำเนิดชนิดหนึ่ง. อย่างไรก็ตาม วิธีการประมาณความหนาแน่นแก่นใช้การคำนวณมาก ดังนั้น วิธีการประมาณความหนาแน่นแก่นจึงมีการใช้งานค่อนข้างจำกัด ในทางปฏิบัติ. และข้อจำกัดนี้ จะเห็นได้ชัดมากขึ้น เมื่อจำนวนข้อมูลมีมากขึ้น หรือข้อมูลมีมิติมากขึ้น.
วิธีการประมาณความหนาแน่นแก่น ประมาณการแจกแจงความน่าจะเป็น ที่ \(\boldsymbol{v} \in \mathbb{R}^M\) จากข้อมูล \(\boldsymbol{d}_i \in \mathbb{R}^M\) สำหรับ \(i = 1, \ldots, N\) โดยคำนวณ \[\begin{eqnarray} \hat{p}(\boldsymbol{v}) = \frac{1}{\sqrt{2\pi\sigma^2}} \cdot z(\boldsymbol{v}) \label{eq: KDE shell} \end{eqnarray}\] เมื่อ \[\begin{eqnarray} z(\boldsymbol{v}) = \frac{1}{N} \sum_{i=1}^N \exp \left( - \frac{\| \boldsymbol{v} - \boldsymbol{d}_i \|^2}{2 \sigma^2} \right) \label{eq: KDE kernel} \end{eqnarray}\] และ \(\sigma\) เป็นอภิมานพารามิเตอร์ ซึ่งควบคุมความราบรื่นความต่อเนื่องของผลลัพธ์.
ตัวหารในสมการ \(\eqref{eq: KDE shell}\) ทำเพื่อให้ \(\hat{p}(\boldsymbol{v})\) มีคุณสมบัติความหนาแน่นความน่าจะเป็นที่ถูกต้อง. เพื่อการสร้างแผนที่ความร้อน การคำนวณเฉพาะค่า \(z\) ที่ตำแหน่งต่าง ๆ ก็เพียงพอ. นั่นคือ สำหรับภาพขนาด \(H \times W\) แผนที่ความร้อน \(\boldsymbol{Z} = [z([c, r]^T)]\) สำหรับ \(c = 0, \ldots, W-1\) และ \(r = 0, \ldots, H-1\). จากนั้น \(\boldsymbol{Z}\) จะถูกนำไปวาดบนภาพสี โดยการแปลงค่า \(z\) ที่แต่ละพิกเซลเป็นสีตามแต่ระบบสีที่จะเลือกใช้.
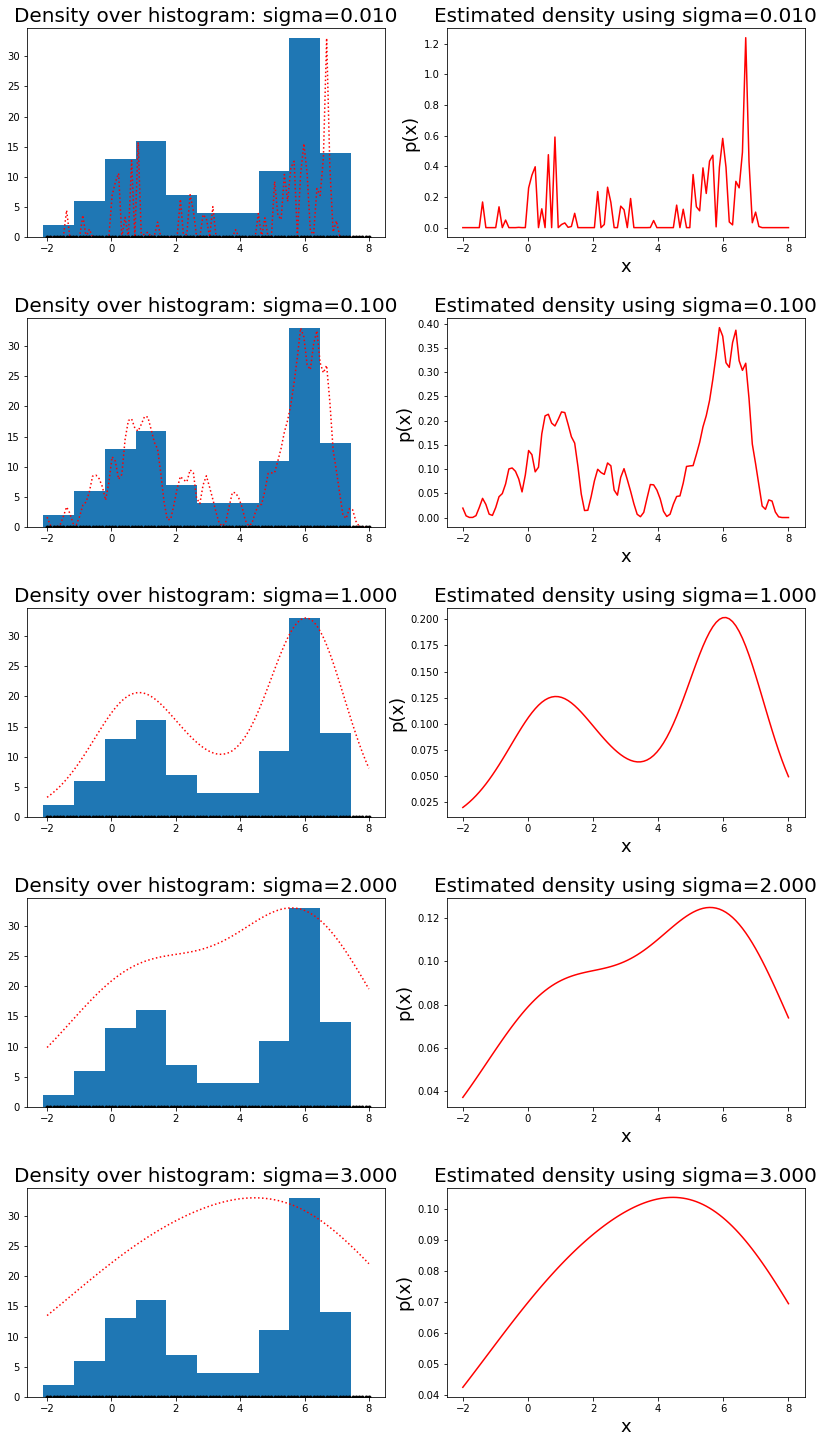
รูป 1.13 แสดงผลการประมาณความหนาแน่นความน่าจะเป็น ด้วยวิธีการประมาณความหนาแน่นแก่น เมื่อใช้ค่า \(\sigma\) ต่าง ๆ. ค่า \(\sigma\) อาจมองเหมือนเป็นการปรับความเรียบของความหนาแน่นที่จะประมาณ หรืออาจเปรียบเสมือนสมมติฐานเบื้องต้น เกี่ยวกับการความหนาแน่นของข้อมูล ว่าข้อมูลมีความหนาแน่นที่มีลักษณะเป็นการแจกแจงฐานนิยมเดี่ยว (unimodal distribution) หรือแบบพหุฐาน (multimodal) และการแจกแจกมีความหลากหลาย มีความซับซ้อนมากขนาดไหน. ภาพในรูป แสดง ค่า \(\sigma\) ขนาดเล็กให้ผลการประมาณความหนาแน่นที่มีความซับซ้อนมาก มีจำนวนฐานมาก ฐานแคบ. ค่า \(\sigma\) ขนาดใหญ่ให้ผลการประมาณความหนาแน่นที่ซับซ้อนน้อย มีจำนวนฐานน้อยลง และความหนาแน่นมีการกระจายตัวออกไปมากขึ้น ฐานกว้าง.
4.1.6 การประเมินผลการตรวจจับ
การประเมินผลเป็นหัวใจของงานการเรียนรู้ของเครื่อง เป็นหัวใจของงานวิศวกรรมและวิทยาศาสตร์ และเป็นหัวใจของ น่าจะเรียกได้ว่า ทุกภาระกิจ. การประเมินผลการตรวจจับวัตถุ อาจทำได้หลายวิธี. หนึ่งในวิธีทีี่นิยม คือ การประเมินด้วยค่าเฉลี่ยค่าประมาณความเที่ยงตรง.
ค่าเฉลี่ยค่าประมาณความเที่ยงตรง (mean Average Precision คำย่อ mAP) เป็นตัวชี้วัดที่นิยมใช้ประเมินคุณภาพระบบตรวจจับภาพวัตถุ. ค่าเฉลี่ยค่าประมาณความเที่ยงตรงสามารถใช้ประเมินความแม่นยำในการตรวจจับตำแหน่ง พร้อมกับประเมินความแม่นยำในการทายชนิดของวัตถุ โดยเป็นการประเมินความสามารถของระบบโดยรวม ไม่เฉพาะเจาะจงกับการเลือกระดับค่าขีดแบ่ง. (ดูแบบฝึกหัด [ex: binding affinity] สำหรับตัวอย่างผลจากการเลือกระดับค่าขีดแบ่งที่ต่างกัน.) ค่าเฉลี่ยค่าประมาณความเที่ยงตรง สามารถคำนวณได้จาก \[\begin{eqnarray} \mathrm{mAP} &=& \frac{1}{K} \sum_{k \in \mathrm{Classes}} \mathrm{AP}_k \label{eq: mAP} \end{eqnarray}\] เมื่อ \(\mathrm{Classes}\) คือเซตของฉลากกลุ่มต่าง ๆ ที่เกี่ยวข้อง. ค่า \(K\) คือจำนวนของชนิดฉลากที่เกี่ยวข้อง (ขนาดของเซต \(\mathrm{Classes}\)). ค่า \(\mathrm{AP}_k\) คือค่าประมาณความเที่ยงตรงของสำหรับการตรวจจับภาพของวัตถุชนิด \(k\).
ค่าประมาณความเที่ยงตรงของวัตถุแต่ละชนิด \(\mathrm{AP}_k\) สามารถประเมินได้จาก \[\begin{eqnarray} \mathrm{AP}_k = \sum_{j \in \mathrm{Ranks}} p_{kj} \cdot \Delta r_{kj} \label{eq: mAP class AP} \end{eqnarray}\] เมื่อ \(\mathrm{Ranks}\) คือเซตลำดับของผลลัพธ์การตรวจพบวัตถุชนิด \(k\). ค่า \(p_{kj}\) เป็นค่าความเที่ยงตรงสำหรับชนิด \(k\) ที่ลำดับ \(j\). และ \(\Delta r_{kj} = r_{kj} - r_{k,j-1}\) โดย \(r_{kj}\) เป็นค่าการเรียกกลับสำหรับวัตถุชนิด \(k\) ที่ลำดับ \(j\).
 |
 |
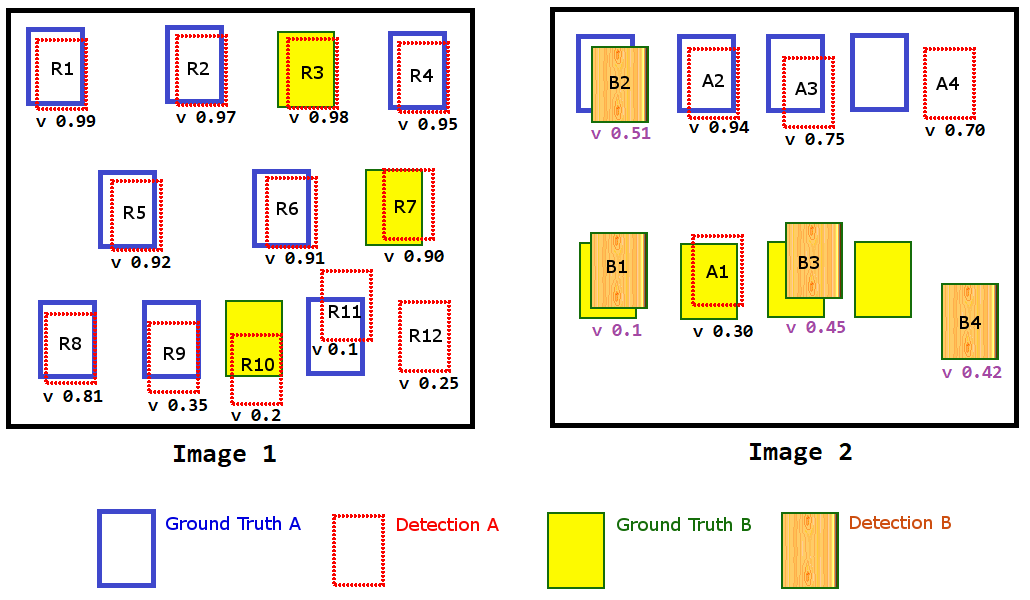
รูป 1.14 แสดงเฉลย และผลการตรวจจับวัตถุสองชนิด จากภาพสองภาพ. แต่ละการตรวจจับจะมีค่าการตรวจจับระบุอยู่ (\(v\) ในภาพ). มีหลายวิธีในการนำความแม่นยำในการตรวจจับตำแหน่ง เข้ามารวมด้วย. วิธีง่าย ๆ อาจใช้วิธีระดับค่าขีดแบ่ง กับการวัดไอโอยู เพื่อตัดการตรวจจับที่ตำแหน่งคลาดเคลื่อนมากทิ้ง. ตัวอย่างเช่น หากกล่องขอบเขตของการตรวจจับ มีค่าไอโอยูกับกล่องขอบเขตเฉลย ต่ำกว่า \(0.5\) ถือว่าผิด นั่นคือเท่ากับ ตรวจจับเกินหนึ่ง สำหรับการตรวจจับลอย และตรวจไม่พบหนึ่ง สำหรับเฉลยที่ไม่มีกล่องขอบเขตตรวจพบ. หรืออาจใช้ค่าไอโอยูเข้าไปคำนวณประกอบกับค่าความมั่นใจอื่น เพื่อสรุปออกมาเป็นค่าการตรวจจับก็ได้ ซึ่งจะทำให้กล่องขอบเขตของการตรวจจับ ที่มีตำแหน่งคลาดเคลื่อนไปมาก จะได้คะแนนค่าการตรวจจับน้อย.
ตัวอย่าง การประเมินค่าเฉลี่ยค่าประมาณความเที่ยงตรง จากรูป 1.14 ค่าเฉลี่ยค่าประมาณความเที่ยงตรงของการตรวจจับ สามารถหาได้จาก (1) เรียงลำดับการตรวจจับตามชนิด (2) ตรวจสอบผลลัพธ์จากการตรวจจับ เปรียบเทียบกับผลเฉลย (3) คำนวณหาค่าความเที่ยงตรง \(p_{kj}\) และค่าการเรียกกลับ \(r_{kj}\) (4) คำนวณพื้นที่ใต้กราฟความเที่ยงตรงและการเรียกกลับ (Area under P-R curve) และ (5) คำนวณพื้นที่ใต้กราฟเฉลี่ยของทุก ๆ ชนิด ซึ่งคือค่าเฉลี่ยค่าประมาณความเที่ยงตรง \(\mathrm{mAP}\). ตาราง 1.1 แสดงตัวอย่างการคำนวณค่าเฉลี่ยค่าประมาณความเที่ยงตรง.
| ผลลัพธ์ | ค่าการตรวจจับ | ความถูกต้อง | ชนิด | \(TP\) | \(FP\) | \(p_{kj}\) | \(r_{kj}\) | \(\Delta r_{kj}\) | \(p_{kj} \cdot \Delta r_{kj}\) |
|---|---|---|---|---|---|---|---|---|---|
| R1 | 0.99 | 1 | A | 1 | 0 | 1.00 | 0.08 | 0.08 | 0.08 |
| R3 | 0.98 | 0 | A | 1 | 1 | 0.50 | 0.08 | 0.00 | 0.00 |
| R2 | 0.97 | 1 | A | 2 | 1 | 0.67 | 0.17 | 0.08 | 0.06 |
| R4 | 0.95 | 1 | A | 3 | 1 | 0.75 | 0.25 | 0.08 | 0.06 |
| A2 | 0.94 | 1 | A | 4 | 1 | 0.80 | 0.33 | 0.08 | 0.07 |
| R5 | 0.92 | 1 | A | 5 | 1 | 0.83 | 0.42 | 0.08 | 0.07 |
| R6 | 0.91 | 1 | A | 6 | 1 | 0.86 | 0.50 | 0.08 | 0.07 |
| R7 | 0.90 | 0 | A | 6 | 2 | 0.75 | 0.50 | 0.00 | 0.00 |
| R8 | 0.81 | 1 | A | 7 | 2 | 0.78 | 0.58 | 0.08 | 0.06 |
| A3 | 0.75 | 1 | A | 8 | 2 | 0.80 | 0.67 | 0.08 | 0.07 |
| A4 | 0.70 | 0 | A | 8 | 3 | 0.73 | 0.67 | 0.00 | 0.00 |
| R9 | 0.35 | 1 | A | 9 | 3 | 0.75 | 0.75 | 0.08 | 0.06 |
| A1 | 0.30 | 0 | A | 9 | 4 | 0.69 | 0.75 | 0.00 | 0.00 |
| R12 | 0.25 | 0 | A | 9 | 5 | 0.64 | 0.75 | 0.00 | 0.00 |
| R10 | 0.20 | 0 | A | 9 | 6 | 0.60 | 0.75 | 0.00 | 0.00 |
| R11 | 0.10 | 1 | A | 10 | 6 | 0.63 | 0.83 | 0.08 | 0.05 |
| \(AP_A =\) | \(0.65\) | ||||||||
| B2 | 0.51 | 0 | B | 0 | 1 | 0 | 0 | 0 | 0 |
| B3 | 0.45 | 1 | B | 1 | 1 | 0.50 | 0.14 | 0.14 | 0.07 |
| B4 | 0.42 | 0 | B | 1 | 2 | 0.33 | 0.14 | 0.00 | 0.00 |
| B1 | 0.10 | 1 | B | 2 | 2 | 0.50 | 0.29 | 0.14 | 0.07 |
| \(AP_B =\) | \(0.14\) | ||||||||
| ค่าเฉลี่ยค่าประมาณความเที่ยงตรง \(\mathrm{mAP} = \mathrm{mean}_k AP_k = \frac{AP_A + AP_B}{2} \approx\) | \(0.40\) | ||||||||
[tbl: mAP Example]
ผลลัพธ์การตรวจหาวัตถุถูกนำมาจัดลำดับตามค่าการตรวจจับ. ค่าการตรวจจับนี้อาจเป็นค่าความน่าจะเป็นที่ระบบตรวจจับวัตถุให้ออกมา หรืออาจจะเป็นค่าอื่นในลักษณะคล้ายกัน เช่น ค่าความมั่นใจ หรือค่าไอโอยู (สมการ \(\eqref{eq: IoU}\)) หรือค่าความน่าจะเป็นคูณกับค่าไอโอยู ก็ได้. ในตัวอย่างนี้ ค่าการตรวจจับที่สูง หมายถึงการตรวจจับได้รับลำดับความสำคัญเป็นลำดับต้น ๆ. สังเกตว่า การจัดลำดับ ทำตามชนิดวัตถุที่ทำนาย เช่น ทุกการตรวจจับวัตถุที่ถูกทำนายเป็นชนิด A จะถูกนำมาจัดลำดับด้วยกัน ไม่ว่าจะเป็นการทำนายที่ภาพใด (หรือผลทำนายถูกหรือไม่ หรือว่าเฉลยจริงเป็นชนิดใด).
แต่ละผลลัพธ์จากการตรวจจับ จะถูกเปรียบเทียบกับผลเฉลย. ในตาราง 1.1 สดมภ์ความถูกต้อง จะระบุเป็น 1 หากมีผลเฉลยชนิดนั้นในตำแหน่งบริเวณนั้น และค่าความถูกต้อง จะระบุเป็น 0 หากไม่ใช่. ตัวอย่างเช่น ในรูป 1.14 ภาพซ้าย กล่องขอบเขต R3, R7, และ R10 ที่ทายตำแหน่งของวัตถุชนิด A แต่บริเวณนั้นไม่มีวัตถุชนิด A อยู่ (มีแต่วัตถุชนิด B) หรือ กล่องขอบเขต R12 ที่ทายตำแหน่งของวัตถุชนิด A แต่บริเวณนั้นไม่มีวัตถุใดอยู่เลย ค่าความถูกต้องของกล่องขอบเขตเหล่านี้ จะเป็นศูนย์.
หากผลลัพธ์จากการตรวจจับถูกต้อง ค่าบวกจริง \(TP\) จะเพิ่มขึ้นหนึ่ง (เริ่มจากลำดับบนสุด) แต่หากผลลัพธ์จากการตรวจจับไม่ถูกต้อง ค่าบวกเท็จ \(FP\) จะเพิ่มขึ้นหนึ่ง (เริ่มจากลำดับบนสุด). ค่าความเที่ยงตรง \(p_{kj}\) ซึ่งเป็นอัตราส่วนการทายถูกต่อการทายทั้งหมด จะสามารถคำนวณได้จาก \(p_{kj} = TP/(TP +FP)\) เมื่อ \(TP\) และ \(FP\) เป็นค่าบวกจริง และค่าบวกเท็จ สำหรับชนิดวัตถุ \(k\) ที่ลำดับ \(j\) เช่น สำหรับการทายวัตถุชนิด A ที่ลำดับแรกสุด นั่นคือ การทายกล่องขอบเขต R1 ทำให้ได้ \(TP = 1, FP = 0\) และ \(p_{A1} = 1\). แต่ที่ลำดับที่สอง (เปรียบเสมือนการตั้งค่าขีดแบ่งอ่อนลง) นั่นคือ การทายกล่องขอบเขต R1 กับกล่องขอบเขต R3 ทำให้ได้ \(TP = 1, FP = 1\) และ \(p_{A2} = 0.5\). ค่าการเรียกกลับ \(r_{kj}\) เป็นอัตราส่วนการทายถูกต่อผลเฉลยทั้งหมด สำหรับชนิดวัตถุ \(k\) ที่ลำดับ \(j\) ซึ่งคำนวณได้จาก \(r_{kj} = TP/N_k\) เมื่อ \(N_k\) คือจำนวนผลเฉลยทั้งหมดของวัตถุชนิด \(k\). ในที่นี้ (ดูรูป 1.14 ประกอบ) จำนวนผลเฉลยทั้งหมดชนิด A หรือ \(N_A = 12\) และ จำนวนผลเฉลยทั้งหมดชนิด B หรือ \(N_B = 7\). ดังนั้น ที่ลำดับล่าง ๆ (เทียบเท่ากับ เมื่อทายมากขึ้น) ค่าการเรียกกลับ \(r_{kj}\) จึงมีแนวโน้มเพิ่มขึ้น เช่น สำหรับการทายวัตถุชนิด A ที่ลำดับที่หนึ่ง (เทียบเท่า การทาย R1 อันเดียว) ค่าการเรียกกลับ \(r_{A1} = 1/12 \approx 0.08\). แต่ที่ลำดับที่สิบหก (ลำดับสุดท้าย เทียบเท่า การทายผลลัพธ์ทั้ง \(16\) อันออกไป) ซึ่งทายถูก \(10\) อัน (\(TP = 10\)) ทำให้ได้ค่าการเรียกกลับ \(r_{A16} = 10/12 \approx 0.83\).
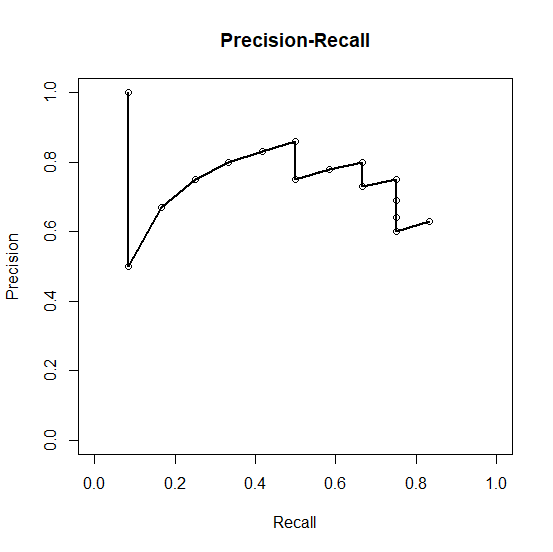
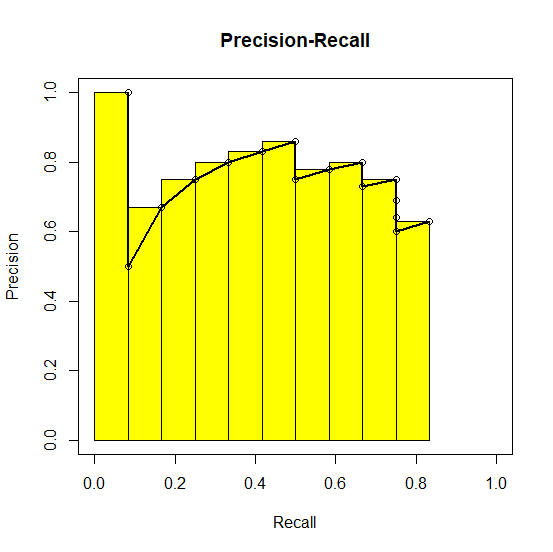
ค่า \(p_{kj}\) และ \(r_{kj}\) ที่ได้สามารถนำมาวาดกราฟความเที่ยงตรงและการเรียกกลับ (Area under P-R curve) ได้. รูป 1.16 (ภาพซ้าย) แสดงกราฟความเที่ยงตรงและการเรียกกลับของการตรวจจับวัตถุชนิด A. ค่าประมาณความเที่ยงตรงเป็นการประมาณพื้นที่ใต้กราฟความเที่ยงตรงและการเรียกกลับ. หากพื้นที่ใต้กราฟมีขนาดใหญ่ หมายถึงคุณภาพที่ดีของตรวจจับภาพวัตถุ. การประมาณพื้นที่ใต้กราฟความเที่ยงตรงและการเรียกกลับของการตรวจจับวัตถุชนิด A แสดงในรูป 1.16 (ภาพขวา).
การประมาณพื้นที่ใต้กราฟความเที่ยงตรงและการเรียกกลับ อาจใช้วิธีการคำนวณสี่เหลี่ยมคางหมูที่ช่วยให้ได้พื้นที่ที่แม่นยำกว่าได้ แต่โดยทั่วไปแล้ว การประมาณคร่าว ๆ ด้วยสี่เหลี่ยมก็เพียงพอ. พื้นที่ใต้กราฟ หรือค่าประมาณความเที่ยงตรงของวัตถุแต่ละชนิด จะถูกนำมาเฉลี่ยกัน เพื่อคำนวณเป็นค่าเฉลี่ยค่าประมาณความเที่ยงตรง เช่นในตัวอย่างนี้ \(mAP = 0.40\).
4.2 ซัพพอร์ตเวกเตอร์แมชชีน
ซัพพอร์ตเวกเตอร์แมชชีน (Support Vector Machine คำย่อ SVM) เป็นแบบจำลองจำแนกค่าทวิภาค ในแนวทางฟังก์ชันแบ่งแยก ซึ่งแปลงค่าอินพุต \(\boldsymbol{x} \in \mathbb{R}^D\) ไปเป็นเอาต์พุต \(\hat{y} \in \{-1, +1\}\) โดยตรง และไม่มีความเชื่อมโยงกับค่าความน่าจะเป็น. กลไกการทำงานของซัพพอร์ตเวกเตอร์แมชชีน อาศัยการแปลงข้อมูลจากปริภูมิของข้อมูลต้นฉบับไปสู่ปริภูมิใหม่ ซึ่งอาจเรียกว่า ปริภูมิลักษณะสำคัญ (feature space) โดยปริภูมิลักษณะสำคัญนี้จะช่วยให้การแบ่งแยกข้อมูลออกเป็นกลุ่มได้ง่ายขึ้น และอาศัยอภิระนาบในปริภูมิลักษณะสำคัญ เพื่อตัดแบ่งแยกข้อมูลออกเป็นสองกลุ่ม.
อภิระนาบ (hyperplane) หมายถึง ระนาบในปริภูมิหลายมิติ. ในปริภูมิสองมิติ อภิระนาบ จะหมายถึง เส้นตรง. นั่นคือ อภิระนาบ จะสามารถระบุได้ด้วยสมการ \(w_1 x_1 + w_2 x_2 + b = 0\) เมื่อ \(\boldsymbol{x} = [x_1, x_2]^T\) เป็นตัวแปรในปริภูมิ และ \(\boldsymbol{w} = [w_1, w_2]^T\) กับ \(b\) เป็นค่าสัมประสิทธิ์. ในปริภูมิสามมิติ อภิระนาบ จะหมายถึง ระนาบ (แผ่นตรงเรียบ ในสามมิติ). นั่นคือ อภิระนาบ จะสามารถระบุได้ด้วยสมการ \(w_1 x_1 + w_2 x_2 + w_3 x_3 + b = 0\) เมื่อ \(\boldsymbol{x} = [x_1, x_2, x_3]^T\) เป็นตัวแปรในปริภูมิ. ในปริภูมิ \(D\) มิติ อภิระนาบ อาจจะยากที่จะจินตนาการ แต่อภิระนาบ ก็จะสามารถระบุได้ด้วยสมการ \(\boldsymbol{w}^T \boldsymbol{x} + b = 0\) เมื่อ \(\boldsymbol{w}, \boldsymbol{x} \in \mathbb{R}^D\).
 |
 |
 |
 |
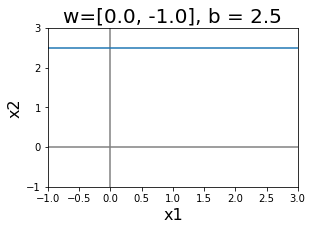
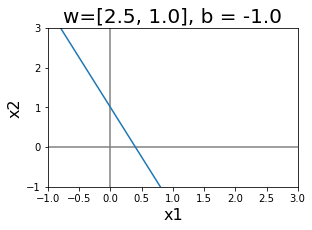 |
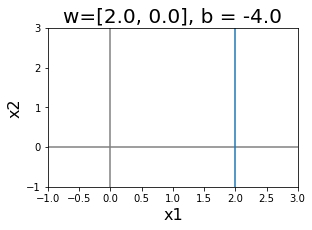
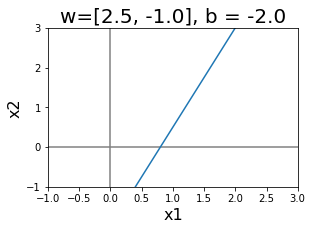
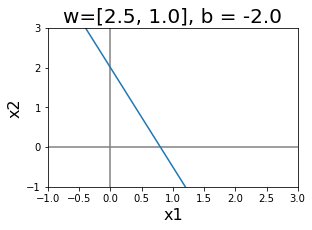
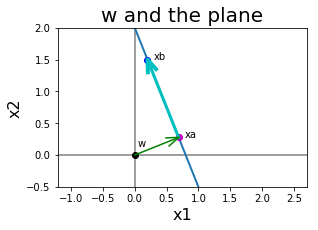
รูป 1.21 แสดงอภิระนาบในสองมิติ. สังเกตความสัมพันธ์ระหว่างทิศทางและตำแหน่งของอภิระนาบ กับค่าของ \(\boldsymbol{w}\) และ \(b\). หากกำหนดให้ \(\boldsymbol{x}_a\) และ \(\boldsymbol{x}_b\) เป็นจุดใด ๆ บนระนาบ. นั่นคือ \(\boldsymbol{w}^T \boldsymbol{x}_a + b = 0\) และ \(\boldsymbol{w}^T \boldsymbol{x}_b + b = 0\) เวกเตอร์จาก \(\boldsymbol{x}_a\) ไป \(\boldsymbol{x}_b\) ซึ่งคือ \(\boldsymbol{x}_b - \boldsymbol{x}_a\) เป็นเวกเตอร์ในแนวของระนาบ. ดูรูป 1.23 ภาพซ้ายประกอบ. พิจารณาผลคูณเวกเตอร์ระหว่าง \(\boldsymbol{w}\) กับเวกเตอร์ในแนวระนาบ และจากคุณสมบัติของจุดบนระนาบ ทำให้พบว่า \(\boldsymbol{w}^T \cdot (\boldsymbol{x}_b - \boldsymbol{x}_a)\) \(=\boldsymbol{w}^T \boldsymbol{x}_b - \boldsymbol{w}^T\boldsymbol{x}_a\) \(=\boldsymbol{w}^T \boldsymbol{x}_b + b - \boldsymbol{w}^T\boldsymbol{x}_a -b = 0\). ผลคูณของ \(\boldsymbol{w}\) กับเวกเตอร์ในแนวระนาบ จะเป็นศูนย์เสมอ. นั่นแปลว่า เวกเตอร์ \(\boldsymbol{w}\) ตั้งฉากกับแนวระนาบ. ดังนั้น ทิศทางของระนาบกำหนดด้วยค่าของเวกเตอร์ \(\boldsymbol{w}\).
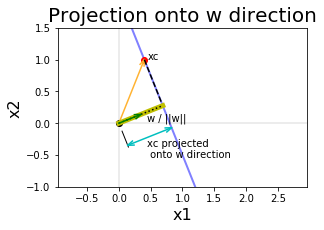
แต่ระนาบจะห่างจากจุดกำเนิดเท่าไร พิจารณารูป 1.23 ภาพขวา. จุดกำเนิด (origin) คือจุด \([0,0]^T\) ในปริภูมิสองมิติ แสดงด้วยจุดกลมสีดำในภาพ (ภาพขวา จุดนี้อาจถูกบังจากเวกเตอร์ต่าง ๆ). ระยะห่างระหว่างจุดกำเนิดกับระนาบ คือระยะจากจุดกำเนิดไประนาบในทิศทางที่ตั้งฉากกับระนาบ. นั่นคือ หากกำหนดให้ \(\boldsymbol{x}_c\) เป็นจุดใด ๆ ในระนาบ ขนาดของภาพฉายของ \(\boldsymbol{x}_c\) ลงบนเวกเตอร์หนึ่งหน่วยในแนว \(\boldsymbol{w}\) จะเป็นระยะทางจากจุดกำเนิดไปถึงระนาบ. ดังนั้น ระยะทางจากจุดกำเนิดไประนาบ สามารถคำนวณได้จาก \(d = \frac{\boldsymbol{w}^T}{\|\boldsymbol{w}\|} \cdot \boldsymbol{x}_c = \frac{\boldsymbol{w}^T \boldsymbol{x}_c}{\|\boldsymbol{w}\|}\) เมื่อ \(d\) คือระยะทางจากจุดกำเนิดไประนาบ. จากคุณสมบัติของระนาบ \(\boldsymbol{w}^T \boldsymbol{x}_c + b = 0\) ทำให้ พบว่า \(d = \frac{-b}{\| \boldsymbol{w}\|}\). หมายเหตุ ขนาดของการฉายภาพเป็นลบ หมายถึงทิศทางของภาพที่ฉาย จะกลับทิศกับเวกเตอร์หนึ่งหน่วยที่เป็นเสมือนฉาก. ถ้า \(b < 0\) ทำให้ ระยะ \(d > 0\) ระนาบจะห่างจุดกำเนิดออกไปขนาด \(|d|\) ทางทิศ \(\boldsymbol{w}\) ถ้า \(b > 0\) ทำให้ ระยะ \(d < 0\) ระนาบจะห่างจุดกำเนิดออกไปขนาด \(|d|\) ทางทิศตรงข้ามกับ \(\boldsymbol{w}\) และถ้า \(b = 0\) หมายถึง ระนาบจะผ่านจุดกำเนิด.
 |
 |
4.2.0.0.1 การวางกรอบปัญหาของซัพพอร์ตเวกเตอร์แมชชีน.
ซัพพอร์ตเวกเตอร์แมชชีน ในปัจจุบันถูกประยุกต์ในงานหลากหลายทั้งงานการหาค่าถดถอย และการจำแนกกลุ่ม แต่ดั้งเดิมเริ่มต้น ซัพพอร์ตเวกเตอร์แมชชีน ถูกออกแบบสำหรับการจำแนกค่าทวิภาค. ข้อมูลจะถูกแบ่งออกเป็น กลุ่มบวก และกลุ่มลบ. แนวคิดของซัพพอร์ตเวกเตอร์แมชชีน คือ การใช้อภิระนาบเป็นเสมือนเส้นแบ่งการตัดสินใจ และข้อมูลฝึกจะถูกนำมาใช้ เพื่อเลือกอภิระนาบในปริภูมิลักษณะสำคัญ ที่ทำให้ช่องว่างที่แบ่งระหว่างจุดข้อมูลกลุ่มบวกกับกลุ่มลบห่างกันมากที่สุด.
ซัพพอร์ตเวกเตอร์แมชชีน อาศัยกลไกที่สำคัญสองอย่าง. กลไกสำคัญแรก คือ การแปลงจุดข้อมูลไปสู่ปริภูมิลักษณะสำคัญ. เนื่องจากอภิระนาบเป็นฟังก์ชันเชิงเส้น บทบาทของการแปลงข้อมูล จะช่วยในการแปลงข้อมูลไปสู่ปริภูมิที่ข้อมูลจะสามารถถูกแบ่งได้ดีด้วยอภิระนาบ. กำหนดให้ลักษณะสำคัญ \(\boldsymbol{z} = \phi(\boldsymbol{x})\) เมื่อ \(\boldsymbol{x}\) เป็นจุดข้อมูลในปริภูมิข้อมูลดั้งเดิม และ \(\phi: \mathbb{R}^D \mapsto \mathbb{R}^M\) เป็นฟังก์ชันที่ใช้แปลงข้อมูลไปสู่ปริภูมิลักษณะสำคัญ โดย \(D\) และ \(M\) คือจำนวนมิติของปริภูมิข้อมูลดั้งเดิมและของปริภูมิลักษณะสำคัญตามลำดับ. ดังนั้น จุดข้อมูล \(\boldsymbol{x}\) (ในปริภูมิข้อมูลดั้งเดิม) จะถูกแทนด้วย \(\boldsymbol{z}\) ในปริภูมิลักษณะสำคัญ. การใช้งานซัพพอร์ตเวกเตอร์แมชชีนให้มีประสิทธิผล เกี่ยวพันโดยตรงกับการเลือกฟังก์ชันลักษณะสำคัญให้เหมาะสม ซึ่งจะได้อภิปรายรายละเอียดในหัวข้อ 1.2.2. หมายเหตุ การเลือกที่จะทำการแบ่งข้อมูลในปริภูมิดั้งเดิม สามารถทำได้ และในหลาย ๆ กรณี ก็เป็นทางเลือกที่เหมาะสม. การเลือกที่จะทำการแบ่งข้อมูลในปริภูมิดั้งเดิม ก็เปรียบเสมือนการเลือกใช้ฟังก์ชันเอกลักษณ์เป็นฟังก์ชันลักษณะสำคัญ นั่นคือ \(\phi(\boldsymbol{x}) = \boldsymbol{x}\) และ \(\boldsymbol{z} = \boldsymbol{x}\).
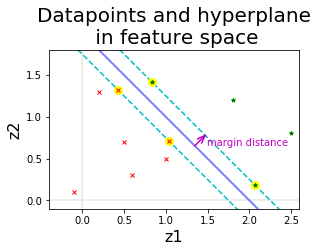
กลไกสำคัญที่สอง คือ การหาอภิระนาบที่ทำให้ขอบเขตของการแบ่งกว้างที่สุด. รูป 1.24 แสดงตัวอย่างความสัมพันธ์ระหว่าง จุดข้อมูลต่าง ๆ ในปริภูมิลักษณะสำคัญ อภิระนาบตัดสินใจ และขอบเขตของการแบ่ง. ออกแบบเพื่อการแบ่งกลุ่มสองกลุ่มโดยเฉพาะ จุดประสงค์ของซัพพอร์ตเวกเตอร์แมชชีน ไม่ใช่แค่หาอภิระนาบใดก็ได้ที่แบ่งข้อมูลได้ แต่ต้องการหาอภิระนาบที่แบ่งข้อมูลได้ และแบ่งได้โดยมีขอบเขตของการแบ่ง (margin of separation) ที่กว้างที่สุดด้วย. สังเกตว่า ในรูป 1.24 หากเอียงอภิระนาบตัดสินใจเพิ่มขึ้นหรือลดลงเล็กน้อย ผลที่ได้ก็จะยังคงสามารถแบ่งข้อมูลได้สมบูรณ์ แต่ขอบเขตของการแบ่งจะแคบลง.
จุดข้อมูลที่อยู่บนแนวขอบเขตของการแบ่ง ซึ่งเป็นจุดข้อมูลที่อยู่ใกล้กับจุดข้อมูลจากต่างกลุ่มมากที่สุด เป็นจุดที่แบ่งยากที่สุด และอภิระนาบจะถูกกำหนดด้วยจุดข้อมูลเหล่านี้. จุดข้อมูลเหล่านี้จะเรียกว่า ซัพพอร์ตเวกเตอร์ (support vectors) ซึ่งเป็นที่มาของชื่อ ซัพพอร์ตเวกเตอร์แมชชีน. จุดข้อมูลอื่น ๆ ที่อยู่ลึกลงไปในเขตของกลุ่ม เป็นจุดข้อมูลที่แบ่งแยกได้ง่ายกว่า จะไม่มีบทบาทในการกำหนดอภิระนาบ.
ปัญหาการจำแนกค่าทวิภาคในทางปฏิบัติ อาจจะมีขอบเขตของการแบ่ง ที่ซับซ้อนกว่าสถานการณ์ในรูป 1.24 ซึ่งสามารถแบ่งกลุ่มได้อย่างสมบูรณ์ด้วยอภิระนาบ. ในที่นี้ พิจารณาการพัฒนาซัพพอร์ตเวกเตอร์แมชชีน สำหรับกรณีที่ข้อมูลสามารถแบ่งแยกได้สมบูรณ์ก่อน และหัวข้อ 1.2.1 อภิปรายการพัฒนาขยายความสามารถสำหรับกรณีทั่วไป (ซึ่งรวมถึงสถานการณ์ที่ไม่สามารถแบ่งแยกกลุ่มได้สมบูรณ์).
4.2.0.0.2 การหาอภิระนาบ.
หากอภิระนาบตัดสินใจ บรรยายด้วย \(\boldsymbol{w}^T \boldsymbol{z} + b = 0\) และมีข้อมูลฝึก \(\{\boldsymbol{x}_i, y_i\}_{i=1, \ldots, N}\) ซึ่งเทียบเท่า \(\{\boldsymbol{z}_i, y_i\}\) โดย \(\boldsymbol{z}_i = \phi(\boldsymbol{x}_i)\) แล้ว อภิระนาบที่แบ่งแยกข้อมูลได้อย่างสมบูรณ์ คือ อภิระนาบที่มีค่าพารามิเตอร์ \(\boldsymbol{w}\) กับ \(b\) ที่ทำให้ \[\begin{eqnarray} \boldsymbol{w}^T \boldsymbol{z}_i + b &> 0 & \mbox{ เมื่อ } y_i = 1 \nonumber \\ \boldsymbol{w}^T \boldsymbol{z}_i + b &< 0 & \mbox{ เมื่อ } y_i = -1 \label{eq: svm separable starting criteria} \end{eqnarray}\] สำหรับ \(i = 1, \ldots, N\) โดย \(N\) เป็นจำนวนข้อมูลฝึก.
เพื่อความสะดวก กำหนดฟังก์ชันแบ่งแยก \(f\) เป็น \[\begin{eqnarray} f(\boldsymbol{z}) = \boldsymbol{w}^T \boldsymbol{z} + b \label{eq: svm discriminant function}. \end{eqnarray}\]
ผลทายกลุ่ม หรือผลตัดสินใจ \(\hat{y}\) สามารถคำนวณได้จาก \[\begin{eqnarray} \hat{y} = \left\{ \begin{array}{l l} 1 & \mbox{ เมื่อ } f(\boldsymbol{z}) > 0, \\ -1 & \mbox{ เมื่อ } f(\boldsymbol{z}) < 0. \\ \end{array} \right. \label{eq: svm separable yhat} \end{eqnarray}\]
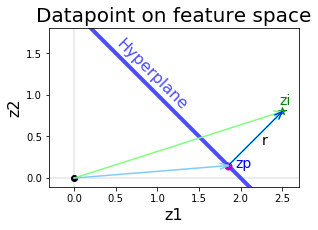
นอกจากแบ่งแยกข้อมูลได้สมบูรณ์แล้ว เรายังต้องการให้ขอบเขตของการแบ่งกว้างที่สุดด้วย. พิจารณาระยะจากอภิระนาบไปสู่จุดข้อมูลใด ๆ. ดูรูป 1.25 ประกอบ. เมื่อแทนจุดใด ๆ ในปริภูมิด้วยเวกเตอร์จากจุดกำเนิดไปจุดนั้น เวกเตอร์ \(\boldsymbol{z}_i\) สามารถเขียนในรูปส่วนประกอบได้ว่า \[\boldsymbol{z}_i = \boldsymbol{z}_p + r \vec{u}\] เมื่อ \(\boldsymbol{z}_p\) คือจุดภาพฉายเชิงตั้งฉากจากจุด \(\boldsymbol{z}_i\) ลงบนอภิระนาบ และ \(\vec{u} = \boldsymbol{w}/\|\boldsymbol{w}\|\) คือเวกเตอร์หนึ่งหน่วยในทิศทางตั้งฉากกับอภิระนาบ และ \(r\) คือระยะห่างระหว่างจุด \(\boldsymbol{z}_i\) กับอภิระนาบ. ดังนั้น จุดใด ๆ \(\boldsymbol{z}_i = \boldsymbol{z}_p + r \boldsymbol{w}/\|\boldsymbol{w}\|\) และค่าฟังก์ชันแบ่งแยก \[\begin{eqnarray} f(\boldsymbol{z}_i) &=& f(\boldsymbol{z}_p + r \boldsymbol{w}/\|\boldsymbol{w}\|) = \boldsymbol{w}^T \cdot (\boldsymbol{z}_p + r \boldsymbol{w}/\|\boldsymbol{w}\|) + b \nonumber \\ &=& \boldsymbol{w}^T \boldsymbol{z}_p + b + r \|\boldsymbol{w}\|^2/\|\boldsymbol{w}\| = r \|\boldsymbol{w}\| \nonumber \\ r &=& \frac{f(\boldsymbol{z}_i)}{\|\boldsymbol{w}\|} \label{eq: svm distance from hyperplane}. \end{eqnarray}\] นั่นคือ ระยะห่างระหว่างจุดใด ๆ \(\boldsymbol{z}_i\) กับอภิระนาบจะเท่ากับค่าฟังก์ชันแบ่งแยกหารด้วยขนาดของ \(\boldsymbol{w}\). ถ้า \(f(\boldsymbol{z}_i) = 0\) ก็คือระยะห่าง \(r = 0\) จุดอยู่บนระนาบ. ถ้า \(f(\boldsymbol{z}_i) > 0\) และจุดนั้นอยู่ห่างระนาบตามคำนวณ ไปทางฝั่งกลุ่มบวก. ถ้า \(f(\boldsymbol{z}_i) < 0\) และจุดนั้นอยู่ห่างระนาบไปทางฝั่งกลุ่มลบ. หมายเหตุ จุดกำเนิด \(\boldsymbol{0}\) จะอยู่ห่างระนาบ \(r = f(\boldsymbol{0})/\|\boldsymbol{w}\| = b/\|\boldsymbol{w}\|\). สังเกตว่า ระยะ \(r\) คือระยะจากระนาบไปจุดใด ๆ ซึ่งเมื่อพิจารณาที่จุดกำเนิด ระยะ \(r\) กับระยะจากจุุดกำเนิดไประนาบ \(d\) (ที่อภิปรายตอนต้นหัวข้อ) จะกลับทิศทางกัน.
พารามิเตอร์ของอภิระนาบที่ทำให้ขอบเขตของการแบ่งกว้างที่สุด อาจเขียนเป็นเงื่อนไขทั่วไปได้ว่า \[\begin{eqnarray} \boldsymbol{w}^T \boldsymbol{z}_i + b & \geq +1 & \mbox{ สำหรับ } y_i = +1 \nonumber \\ \boldsymbol{w}^T \boldsymbol{z}_i + b & \leq -1 & \mbox{ สำหรับ } y_i = -1 \label{eq: svm margin constraints} \end{eqnarray}\] ในสถานการณ์ที่ข้อมูลสามารถแบ่งแยกได้โดยสมบูรณ์ ค่าพารามิเตอร์ \(\boldsymbol{w}\) และ \(b\) ที่ได้ สามารถนำไปปรับขนาดโดยคูณค่าคงที่เข้าไป เพื่อให้เงื่อนไขในอสมการ \(\eqref{eq: svm margin constraints}\) เป็นจริงได้. จุดข้อมูล \(i^{th}\) ที่ทำให้เงื่อนไขในอสมการ \(\eqref{eq: svm margin constraints}\) ทำงาน 3 จะอยู่บนแนวขอบเขตของการแบ่ง และจุดเหล่านี้จะเรียกว่า ซัพพอร์ตเวกเตอร์. (ดูรูป 1.24 ประกอบ). ค่าฟังก์ชันแบ่งแยกของซัพพอร์ตเวกเตอร์ เป็น \[f(\boldsymbol{z}'_i) = \boldsymbol{w}^T \boldsymbol{z}'_i + b = \left\{ \begin{array}{ll} +1 & \mbox{ เมื่อ } y'_i = +1, \\ -1 & \mbox{ เมื่อ } y'_i = -1. \end{array} \right.\] โดย \(\boldsymbol{z}'_i\) และ \(y'_i\) คือค่าลักษณะสำคัญและเฉลยของซัพพอร์ตเวกเตอร์ดัชนี \(i^{th}\).
ระยะจากอภิระนาบไปซัพพอร์ตเวกเตอร์ \(\boldsymbol{z}'_i\) จะเป็น \[r = \frac{f(\boldsymbol{z}'_i)}{\|\boldsymbol{w}\|} = \left\{ \begin{array}{lll} \frac{+1}{\|\boldsymbol{w}\|} & \mbox{ เมื่อ } & y'_i = +1, \\ \frac{-1}{\|\boldsymbol{w}\|} & \mbox{ เมื่อ } & y'_i = -1. \\ \end{array} \right.\] ดังนั้นความกว้างของขอบเขตของการแบ่ง \(\rho = 2 r = 2/\|\boldsymbol{w}\|\) และปัญหาค่ามากที่สุด \(\max_{\boldsymbol{w}, b} \rho = \frac{2}{\|\boldsymbol{w}\|}\) ก็เทียบเท่าปัญหาค่าน้อยที่สุด \(\min_{\boldsymbol{w}, b} \|\boldsymbol{w}\|\). นอกจากนั้น อสมการ \(\eqref{eq: svm margin constraints}\) สามารถเขียนให้กระชับขึ้นได้เป็น \[\begin{eqnarray} y_i \cdot (\boldsymbol{w}^T \boldsymbol{z}_i + b) & \geq 1 \label{eq: svm concise margin constraints}. \end{eqnarray}\] นั่นคือ กรอบปัญหาการฝึกซัพพอร์ตเวกเตอร์แมชชีน สามารถเขียนได้เป็น \[\begin{eqnarray} \underset{\boldsymbol{w}, b}{\mathrm{minimize}} & \frac{1}{2} \boldsymbol{w}^T \boldsymbol{w} & \nonumber \\ \mbox{s.t.} & y_i (\boldsymbol{w}^T \boldsymbol{z}_i + b) \geq 1 & \mbox{ for } i =1, \ldots, N. \label{eq: svm primal separable} \end{eqnarray}\] ฟังก์ชันจุดประสงค์ของซัพพอร์ตเวกเตอร์แมชชีน เป็นคอนเวกซ์ (convex function) และข้อจำกัดเป็นฟังก์ชันเชิงเส้น ซึ่งเหล่านี้ล้วนเป็นคุณสมบัติที่ดี จากมุมมองของการแก้ปัญหาค่าดีที่สุด (หัวข้อ [sec: optimization]) เพราะว่า ลักษณะเหล่านี้ ทำให้ เมื่อแก้ปัญหาและพบค่าทำให้น้อยที่สุดท้องถิ่นแล้ว ค่าทำให้น้อยที่สุดท้องถิ่นจะเป็น ค่าทำให้น้อยที่สุดทั่วหมดด้วย.
การใช้งานซัพพอร์ตเวกเตอร์แมชชีนในทางปฏิบัติจะไม่แก้ปัญหานี้โดยตรง แต่จะใช้คุณสมบัติของภาวะคู่กัน (ดูแบบฝึกหัด [ex: opt duality] เพิ่มเติม) เพื่อแปลงปัญหาในนิพจน์ \(\eqref{eq: svm primal separable}\) ซึ่งเป็นปัญหาปฐม ไปอยู่ในรูปปัญหาคู่ ซึ่งจะสามารถใช้งานได้มีประสิทธิภาพกว่า.
4.2.0.0.3 ปัญหาคู่.
จากวิธีลากรานจ์ จุดประสงค์และข้อจำกัดที่ระบุด้วยนิพจน์ \(\eqref{eq: svm primal separable}\) จะแทนด้วยลากรานจ์ฟังก์ชัน \[\begin{eqnarray} J(\boldsymbol{w}, b, \boldsymbol{\alpha}) = \frac{1}{2} \boldsymbol{w}^T \boldsymbol{w} - \sum_{i=1}^N \alpha_i \cdot \left( y_i \cdot (\boldsymbol{w}^T \boldsymbol{z}_i + b)- 1\right) \label{eq: svm primal lagrange objective} \end{eqnarray}\] เมื่อ \(\boldsymbol{\alpha} = [\alpha_1, \ldots, \alpha_N]^T\) เป็นลากรานจ์พารามิเตอร์ โดย \(\alpha_i \geq 0\) สำหรับ \(i=1, \ldots, N\).
จากทฤษฎีบทคารูชคุนทักเกอร์ (ดูแบบฝึกหัด [ex: opt kkt]) ที่กล่าวว่า หากกำหนดให้ \(\boldsymbol{w}_o\) และ \(b_o\) แทนชุดค่าพารามิเตอร์ที่ดีที่สุด (ค่าทำให้น้อยที่สุด) แล้ว ณ จุดที่ดีที่สุด เงืื่อนไขต่อไปนี้จะต้องเป็นจริง. เงื่อนไขที่หนึ่ง คือ \(\alpha_i \geq 0\) สำหรับทุก ๆ ค่าของ \(i\). เงื่อนไขที่สอง คือ \[\begin{eqnarray} \nabla_{\boldsymbol{w}} J (\boldsymbol{w}_o, b_o, \boldsymbol{\alpha}) = 0 \nonumber \\ \nabla_{b} J(\boldsymbol{w}_o, b_o, \boldsymbol{\alpha}) = 0 \nonumber \end{eqnarray}\] ซึ่งเมื่อหาอนุพันธ์และแก้สมการแล้วจะได้ว่า \[\begin{eqnarray} \boldsymbol{w}_o &=& \sum_{i=1}^N \alpha_i y_i \boldsymbol{z}_i \label{eq: svm w} \\ \sum_{i=1}^N \alpha_i y_i &=& 0 \label{eq: svm dual eq constraint} \end{eqnarray}\] และเงื่อนไขที่สาม คือ \[\sum_{i=1}^N \alpha_i \cdot \left( y_i (\boldsymbol{w}_o^T \boldsymbol{z}_i + b_o) - 1 \right) = 0.\] ดังนั่น เมื่อพิจารณาเงื่อนไขที่หนึ่งกับเงื่อนไขที่สามแล้วจะพบว่า ณ จุดที่ดีที่สุด ถ้า \(\alpha_i > 0\) แล้ว เรารู้แน่ ๆ เลยว่า \(y_i (\boldsymbol{w}_o^T \boldsymbol{z}_i + b_o) - 1 = 0\). นั่นคือข้อจำกัดทำงาน ซึ่งหมายถึง จุดข้อมูลที่ \(i^{th}\) เป็นซัพพอร์ตเวกเตอร์.
กำหนดให้ \(J'\) แทนลากรานจ์ฟังก์ชัน เมื่อใช้ชุดค่าพารามิเตอร์ที่ดีที่สุด (ใช้ \(\boldsymbol{w}_o\) และ \(b_o\)) พร้อมแทนค่าจากสมการ \(\eqref{eq: svm w}\) และ \(\eqref{eq: svm dual eq constraint}\) จะได้ \[J'(\boldsymbol{\alpha}) = \sum_{i=1}^N \alpha_i - \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j \boldsymbol{z}^T_i \boldsymbol{z}_j\] เมื่อ \(\alpha \geq 0\) และ \(\sum_{i=1}^N \alpha_i y_i = 0\). กำหนดให้ ฟังก์ชันเคอร์เนล \(k(\boldsymbol{x}_i, \boldsymbol{x}_j) = \phi(\boldsymbol{x})^T_i \phi(\boldsymbol{x})_j\) \(=\boldsymbol{z}^T_i \boldsymbol{z}_j\).
ดังนั้นปัญหาคู่ สามารถระบุได้เป็น \[\begin{eqnarray} \underset{\boldsymbol{\alpha}}{\mathrm{maximize}} & \sum_{i=1}^N \alpha_i - \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j k(\boldsymbol{x}_i, \boldsymbol{x}_j) \nonumber \\ \mbox{s.t.} & \nonumber \\ & \begin{array}{ll} \sum_{i=1}^N \alpha_i y_i = 0, & \\ \alpha \geq 0 & \mbox{ for } i =1, \ldots, N. \end{array} \label{eq: svm dual separable} \end{eqnarray}\] สังเกตว่า (1) ปัญหาปฐมเป็นปัญหาค่าน้อยที่สุด แต่ปัญหาคู่เป็นปัญหาค่ามากที่สุด 4. (2) ปัญหาคู่อยู่ในรูปของตัวแปร \(\boldsymbol{\alpha}\) เท่านั้น ไม่มี \(\boldsymbol{w}\) ไม่มี \(b\).
หาก \(\boldsymbol{\alpha}^\ast\) เป็นลากรานจ์พารามิเตอร์ที่ดีที่สุดที่หาได้มา แล้วการทำนายกลุ่มของจุดข้อมูล \(\boldsymbol{x}\) สามารถคำนวณได้โดยค่าฟังก์ชันแบ่งแยก \(f(\phi(\boldsymbol{x})) = \boldsymbol{w}_o^T \phi(\boldsymbol{x}) + b_o\). เพื่อความสะดวก นิยาม \(g(\boldsymbol{x}) = \boldsymbol{w}_o^T \phi(\boldsymbol{x}) + b_o\). เมื่อแทนค่าสมการ \(\eqref{eq: svm w}\) เข้าไปแล้วจะได้ \[\begin{eqnarray} g(\boldsymbol{x}) &=& \sum_{i=1}^N \alpha^\ast_i y_i \phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}) + b_o \nonumber \\ &=& \sum_{i=1}^N \alpha^\ast_i y_i k(\boldsymbol{x}_i,\boldsymbol{x}) + b_o \label{eq: svm score function} \end{eqnarray}\] เมื่อ \(\boldsymbol{x}_i, y_i\) คือจุดข้อมูลฝึก.
เนื่องจากตัวแปร \(\alpha^\ast_i\) ทำหน้าที่ของลากรานจ์พารามิเตอร์ ดังนั้น สำหรับข้อจำกัดที่ไม่ได้ทำงาน ซึ่งสัมพันธ์กับจุดข้อมูลที่อยู่ลึกลงไปในกลุ่ม ไม่ได้อยู่บริเวณขอบเขตของการแบ่ง ไม่ใช่ซัพพอร์ตเวกเตอร์ ค่า \(\alpha^\ast_i\) ของจุดข้อมูลเหล่านั้นจะเป็นศูนย์ (เงื่อนไขที่สามและที่หนึ่งของคารูชคุนทักเกอร์). สำหรับ \(\alpha^\ast_i = 0\) ไม่ได้ส่งผลต่อการคำนวณสมการ \(\eqref{eq: svm score function}\) เลย. ดังนั้น การใช้ซัพพอร์ตเวกเตอร์แมชชีนอนุมานกลุ่ม จึงไม่จำเป็นต้องใช้ข้อมูลทุกตัว ใช้เฉพาะซัพพอร์ตเวกเตอร์ก็พอ. นั่นคือ ค่าการอนุมานกลุ่ม คำนวณจาก \[\begin{eqnarray} g(\boldsymbol{x}) &=& \sum_{i \in S} \alpha^\ast_i y_i k(\boldsymbol{x}_i,\boldsymbol{x}) + b_o \label{eq: svm discriminant function support vectors} \end{eqnarray}\] เมื่อ \(S\) คือ เซตของดัชนีของซัพพอร์ตเวกเตอร์ นั่นคือ \(S = \{i: \alpha^\ast_i > 0\}\).
สำหรับค่าของพารามิเตอร์ \(b_o\) พิจารณาจากซัพพอร์ตเวกเตอร์ (\(i \in S\)) ที่มี \(\alpha^\ast_i > 0\). จากทฤษฎีบทของคารูชคุนทักเกอร์ทำให้รู้ว่า ถ้า \(\alpha^\ast_i > 0\) หมายถึง เงื่อนไข \(y_i (\boldsymbol{w}_o^T \boldsymbol{z}_i + b_o) \geq 0\) ทำงาน. นั่นคือ สำหรับ \(i \in S\) แล้ว \[\begin{eqnarray} y_i \cdot g(\boldsymbol{x}_i) &=& 1 \label{eq: svm active constraints for b} \\ y_i \cdot (\sum_{j \in S} \alpha^\ast_j y_j k(\boldsymbol{x}_j,\boldsymbol{x}_i) + b_o) &=& 1 \label{eq: svm solve for b}. \end{eqnarray}\] เมื่อคูณ \(y_i\) เข้าไปทั้งสองข้าง (ซึ่ง \(y_i^2 = 1\)) และจัดรูปใหม่จะได้ \[\begin{eqnarray} b_o &=& y_i - \sum_{j \in S} \alpha^\ast_j y_j k(\boldsymbol{x}_j,\boldsymbol{x}_i) \nonumber \end{eqnarray}\] การคำนวณ อาจสุ่มเลือกดัชนี \(i\) ของซัพพอร์ตเวกเตอร์ขึ้นมาหนึ่งตัว หรือที่นิยม คือการใช้ค่าเฉลี่ย \[\begin{eqnarray} b_o &=& \frac{1}{|S|} \sum_{i \in S} \left( y_i - \sum_{j \in S} \alpha^\ast_j y_j k(\boldsymbol{x}_j,\boldsymbol{x}_i) \right) \label{eq: svm b} \end{eqnarray}\] เมื่อ \(|S|\) คือจำนวนของซัพพอร์ตเวกเตอร์.
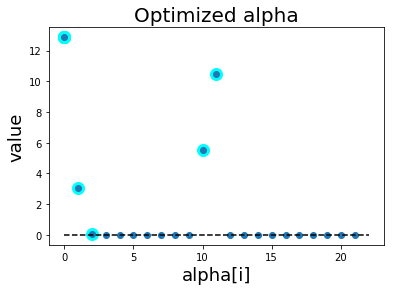
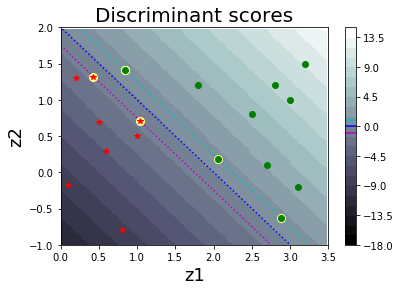
ตัวอย่างผลลัพธ์จากการฝึกซัพพอร์ตเวกเตอร์แมชชีน แสดงในรูป 1.27. ภาพซ้ายเป็นค่า \(\boldsymbol{\alpha}\) ที่ได้จากการฝึก. ภาพขวาแสดงค่าฟังก์ชันแบ่งแยก ที่คำนวณจากสมการ \(\eqref{eq: svm discriminant function support vectors}\). ซัพพอร์ตเวกเตอร์ คือจุดข้อมูลที่เน้น ดังแสดงในภาพขวา ซึ่งระบุได้จากค่า \(\alpha_i\) ที่สัมพันธ์กับมันมีค่ามากกว่าศูนย์.
 |
 |
4.2.1 สถานการณ์ที่ไม่สามารถแบ่งแยกกลุ่มได้สมบูรณ์
ในทางปฏิบัติ การแจกแจงของกลุ่มข้อมูลอาจจะทำให้บริเวณของข้อมูลมีการซ้อนทับกันได้. สมมติฐานการแบ่งแยกได้อย่างสมบูรณ์ อาจจะทำให้ได้แบบจำลองที่การโอเวอร์ฟิต ขาดคุณสมบัติความทั่วไป. ดังนั้น เพื่อผ่อนสมมติฐานการแบ่งแยกได้อย่างสมบูรณ์ ควรจะยอมให้มีบางจุดข้อมูลที่อาจล้ำเข้าไปในขอบเขตของการแบ่งบ้าง หรือแม้แต่ยอมให้มีบางจุดข้อมูลที่ถูกจำแนกกลุ่มผิดบ้าง.
ซัพพอร์ตเวกเตอร์แมชชีนผ่อนปรนสมมติฐานการแบ่งแยกสมบูรณ์ลง ด้วยการผ่อนปรนข้อจำกัดของขอบเขตของการแบ่ง (อสมการ \(\eqref{eq: svm margin constraints}\)) ผ่านกลไกของตัวแปรช่วย \(\xi_i\) เป็น \[\begin{eqnarray} \boldsymbol{w}^T \boldsymbol{z}_i + b & \geq +1 - \xi_i & \mbox{ สำหรับ } y_i = +1 \nonumber \\ \boldsymbol{w}^T \boldsymbol{z}_i + b & \leq -1 + \xi_i & \mbox{ สำหรับ } y_i = -1 \label{eq: svm margin xi constraints} \end{eqnarray}\] โดย \(\xi_i \geq 0\) สำหรับ \(i = 1, \ldots, N\) เมื่อ \(N\) เป็นจำนวนข้อมูลฝึก.
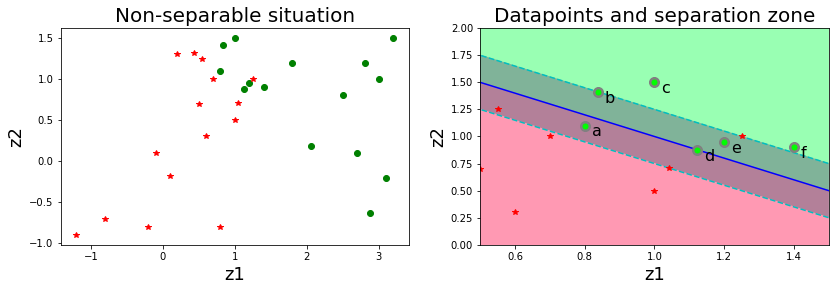
ดังนั้น ถ้า \(\xi_i = 0\) หมายถึง จุดข้อมูลที่ \(i^{th}\) จะอยู่ห่างอภิระนาบออกมาทางกลุ่มที่ถูกต้อง และอยู่นอกขอบเขตของการแบ่ง. รูป 1.28 แสดงตัวอย่างต่าง ๆ เมื่อผ่อนปรนเงื่อนไขแบ่งแยกสมบูรณ์ลง. โดยในรูป จุด b, จุด c, และจุด f จะมี \(\xi_b, \xi_c, \xi_f = 0\). ถ้า \(\xi_i > 0\) หมายถึง จุดข้อมูลที่ \(i^{th}\) อยู่ล้ำแนวของขอบเขตของการแบ่งออกไป. ในรูป จุด a, จุด d, และจุด e จะมี \(\xi_a, \xi_d, \xi_e > 0\).
พิจารณากรณี ที่ \(0 < \xi_i < 1\) นั่นคือ จุดข้อมูลอยู่ล้ำแนวของขอบเขตของการแบ่งออกไป แต่ยังไม่ถึงอภิระนาบ เช่น จุด e ในรูป จะมี \(0 < \xi_e < 1\). และเนื่องจากจุดข้อมูลยังอยู่ฝั่งของกลุ่มอยู่ จุดข้อมูลที่มี \(0 < \xi_i < 1\) จะยังถูกจำแนกได้ถูกต้อง. กรณีที่ \(\xi_i = 1\) นั่นคือ จุดข้อมูลอยู่ล้ำแนวของขอบเขตของการแบ่งออกไป และไปอยู่บนอภิระนาบพอดี เช่น ในรูป \(\xi_d = 1\). กรณีที่ \(\xi_i > 1\) นั่นคือ จุดข้อมูลอยู่ล้ำแนวของขอบเขตของการแบ่งออกไปมาก มากจนเลยแนวของอภิระนาบ ข้ามไปอยู่อีกฝั่งของการจำแนก ดังนั้น จุดข้อมูลจะถูกจำแนกผิด เช่น ในรูป \(\xi_a > 1\).
เงื่อนไขในอสมการ \(\eqref{eq: svm margin xi constraints}\) เขียนให้กระชับขึ้นเป็น \[\begin{eqnarray} y_i \left( \boldsymbol{w}^T \boldsymbol{z}_i + b \right) &\geq 1 - \xi_i & \mbox{ สำหรับ } i = 1, \ldots, N \label{eq: svm margin xi concise} \end{eqnarray}\] เมื่อ \(\xi_i \geq 0\). การปรับเงื่อนไขนี้ เปรียบเสมือนการปรับจากข้อจำกัดที่เข้มงวด ผ่อนปรนลงมาเป็นข้อจำกัดที่อ่อนลง. กรอบปัญหา จึงถูกวางใหม่เป็น \[\begin{eqnarray} \underset{\boldsymbol{w}, b, \boldsymbol{\xi}}{\mathrm{minimize}} & \frac{1}{2} \boldsymbol{w}^T \boldsymbol{w} + C \sum_{i=1}^N \xi_i \nonumber \\ \mbox{s.t.} & \begin{array}{ll} y_i \left( \boldsymbol{w}^T \phi(\boldsymbol{x}_i) + b \right) \geq 1 - \xi_i & \mbox{ for } i =1, \ldots, N \end{array} \label{eq: csvm primal} \end{eqnarray}\] เมื่อ \(C > 0\). อภิมานพารามิเตอร์ \(C\) เป็นเหมือนค่าที่ใช้ควบคุมความเข้มงวดของข้อจำกัด. ค่า \(C\) ที่เล็กจะยอมให้มีการจำแนกผิดได้มากขึ้น ในขณะที่ค่า \(C\) ใหญ่จะบังคับให้แบบจำลองจำแนกผิดให้น้อยลง.
4.2.1.0.1 ปัญหาคู่.
ในทำนองเดียวกัน ลากรานจ์ฟังก์ชันของปัญหาปฐม (นิพจน์ \(\eqref{eq: csvm primal}\)) คือ \[J(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}) = \frac{1}{2} \boldsymbol{w}^T \boldsymbol{w} + C \sum_{i=1}^N \xi_i - \sum_{i=1}^N \alpha_i \cdot \left(y_i \left( \boldsymbol{w}^T \phi(\boldsymbol{x}_i) + b \right) - 1 + \xi_i\right) - \sum_{i=1}^N \beta_i \xi_i\] โดย \(\alpha_i, \beta_i \geq 0\). ทั้ง \(\alpha_i\) และ \(\beta_i\) เป็นลากรานจ์พารามิเตอร์.
จากทฤษฎีบทคารูชคุนทักเกอร์ ณ จุดที่ดีที่สุด ค่าพารามิเตอร์ที่ดีที่สุด \(\boldsymbol{w}_o, b, \boldsymbol{\xi}_o\) จะทำให้เงื่อนไขดังนี้เป็นจริง. เงื่อนไขที่หนึ่ง \(\alpha_i \geq 0\) และ \(\beta_i \geq 0\). เงื่อนไขที่สอง \[\begin{eqnarray} \nabla_{\boldsymbol{w}} J (\boldsymbol{w}_o, b, \boldsymbol{\xi}_o) = 0 \nonumber \\ \nabla_{b} J (\boldsymbol{w}_o, b, \boldsymbol{\xi}_o) = 0 \nonumber \\ \nabla_{\boldsymbol{\xi}} J (\boldsymbol{w}_o, b, \boldsymbol{\xi}_o) = 0 \nonumber . \end{eqnarray}\] หลังจากหาอนุพันธ์และแก้สมการแล้ว สรุปได้ว่า \[\begin{eqnarray} \boldsymbol{w}_o &=& \sum_{i=1}^N \alpha_i y_i \phi(\boldsymbol{x}_i) \label{eq: kkt2 w} \\ \sum_{i=1}^N \alpha_i y_i &=& 0 \label{eq: kkt2 b} \\ C - \alpha_i - \beta_i &=& 0 \mbox{ for } i =1, \ldots, N \label{eq: kkt2 xi}. \end{eqnarray}\] สมการ \(\eqref{eq: kkt2 xi}\) คือ \(\beta_i = C - \alpha_i\). แทนค่าเหล่านี้ เข้าไปในลากรานจ์ฟังก์ชันแล้ว ลากรานจ์ฟังก์ชัน ณ จุดที่ดีที่สุด \(J'\) สามารถเขียนได้ว่า \[\begin{eqnarray} J'(\boldsymbol{\alpha}) &=& \sum_{i=1}^N \alpha_i -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j k(\boldsymbol{x}_i, \boldsymbol{x}_j) \label{eq: csvm J'} \end{eqnarray}\] เมื่อ \(\sum_{i=1}^N \alpha_i y_i = 0\) และ \(\alpha_i \geq 0\) กับ \(\beta_i \geq 0\). แต่ \(\beta_i \geq 0\) เทียบเท่ากับ \(\alpha_i \leq C\). ดังนั้นปัญหาคู่สามารถระบุได้เป็น \[\begin{eqnarray} \underset{\boldsymbol{\alpha}}{\mathrm{maximize}} & \sum_{i=1}^N \alpha_i - \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j k(\boldsymbol{x}_i, \boldsymbol{x}_j) \nonumber \\ \mbox{s.t.} & \nonumber \\ & \begin{array}{ll} \sum_{i=1}^N \alpha_i y_i = 0, & \\ 0 \leq \alpha_i \leq C & \mbox{ for } i =1, \ldots, N. \end{array} \label{eq: svm dual} \end{eqnarray}\] สังเกตุว่า ปัญหาคู่สำหรับกรณีทั่วไป แทบจะเหมือนกับปัญหาคู่กรณีข้อมูลแบ่งแยกได้โดยสมบูรณ์เลย ต่างกันเพียงแต่เงื่อนไขของค่า \(\alpha_i\) ที่เปลี่ยนมาเป็น \(0 \leq \alpha_i \leq C\).
การอนุมานค่าฟังก์ชันแบ่งแยกก็ทำได้โดยการคำนวณสมการ \(\eqref{eq: svm score function}\) เช่นเดิม. และค่าพารามิเตอร์ \(b_o\) ในกรณีที่ข้อมูลไม่สามารถแบ่งแยกได้สมบูรณ์ สามารถพิจารณาจาก เงื่อนไข \(y_i \left( \boldsymbol{w}^T \boldsymbol{z}_i + b \right) \geq 1 - \xi_i\) (อสมการ \(\eqref{eq: svm margin xi concise}\)) ที่เมื่อ \(\alpha_i > 0\) แล้ว เงื่อนไขจะทำงาน. นั่นคือ \(y_i \left( \boldsymbol{w}^T \boldsymbol{z}_i + b \right) = 1 - \xi_i\). แต่เรายังไม่สามารถแก้สมการนี้ได้ เพราะเรายังไม่รู้ค่า \(\xi_i\). อย่างไรก็ตาม จากการที่ \(\xi_i \geq 0\) เป็นเงื่อนไข ที่ควบคุมด้วยลากรานจ์พารามิิเตอร์ \(\beta_i\). นั่นคือ เรารู้ว่า เมื่อ \(\beta_i > 0\) (เทียบเท่า \(\alpha_i < C\)) แล้ว เงื่อนไขจะทำงาน ซึ่งคือ \(\xi_i = 0\). ดังนั้น จุดข้อมูลที่ \(0 < \alpha_i < C\) จะบอกได้ว่า \(y_i \left( \boldsymbol{w}^T \boldsymbol{z}_i + b \right) = 1\) ซึ่งเราสามารถใช้จุดข้อมูลเหล่านี้ แก้สมการหาค่า \(b_o\) ได้. นั่นคือ \[\begin{eqnarray} y_i \cdot g(\boldsymbol{x}_i) &=& 1 \mbox{ เมื่อ } i \in \{j: 0 < \alpha_j < C \} \label{eq: non-sep for b} \\ \sum_{j \in S} \alpha^\ast_j y_j k(\boldsymbol{x}_j,\boldsymbol{x}_i) + b_o &=& y_i \nonumber \\ b_o &=& y_i - \sum_{j \in S} \alpha^\ast_j y_j k(\boldsymbol{x}_j,\boldsymbol{x}_i) \label{eq: svm b general}. \end{eqnarray}\] เช่นเดียวกัน \(i\) อาจเลือกจากดัชนีหนึ่ง ซึ่งทำให้ \(0 < \alpha_i < C\) หรือ อาจใช้ค่าเฉลี่ย ซึ่งคือ \[\begin{eqnarray} b_o &=& \frac{1}{|S'|} \sum_{i \in S'} \left( y_i - \sum_{j \in S} \alpha^\ast_j y_j k(\boldsymbol{x}_j,\boldsymbol{x}_i) \right) \label{eq: svm bo} \end{eqnarray}\] เมื่อ \(S = \{i: \alpha_i > 0\}\) และ \(S' = \{i: 0 < \alpha_i < C\}\) เป็นเซตดัชนีของซัพพอร์ตเวกเตอร์ และซัพพอร์ตเวกเตอร์ที่แนวขอบเขตของการแบ่ง ตามลำดับ. หมายเหตุ \(S\) มาจากสมการ \(\eqref{eq: kkt2 w}\) ที่คำนวณทุกตัว แต่ \(\alpha_i = 0\) ไม่มีผล ดังนั้นจึงเลือกเฉพาะที่ \(\alpha_i > 0\) มาคำนวณ เพื่อลดการคำนวณที่ไม่จำเป็นและลดข้อมูล \((\boldsymbol{x}_i, y_i)\) ที่ต้องเก็บรักษาไว้. ส่วน \(S'\) มาจากทฤษฎีบทคารูชคุนทักเกอร์ที่ทำให้อสมการ \(\eqref{eq: svm margin xi concise}\) เปลี่ยนมาอยู่ในรูปสมการ \(\eqref{eq: non-sep for b}\) เพื่อทำให้สามารถคำนวณค่า \(b_o\) ได้.
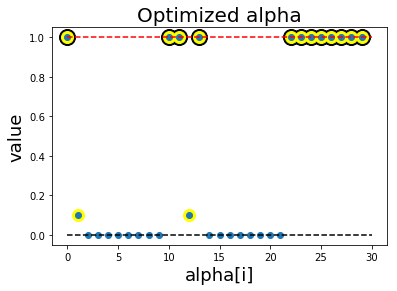
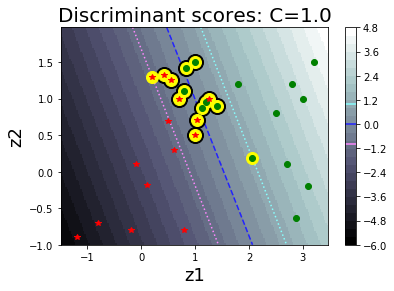
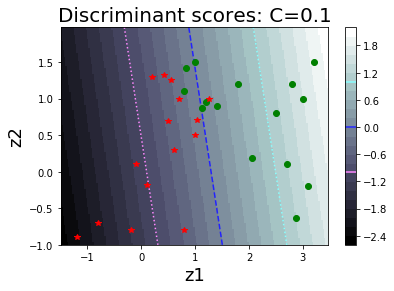
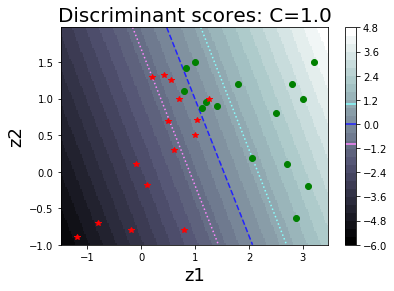
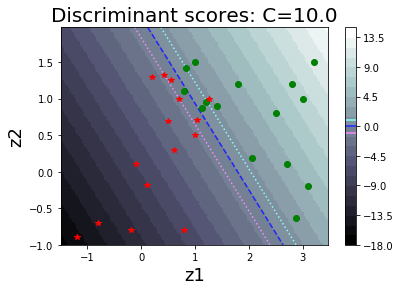
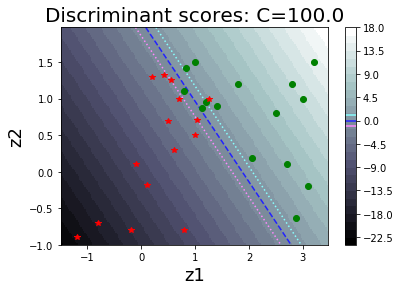
รูป 1.30 แสดงค่า \(\alpha_i\) ต่าง ๆ ที่ฝึกเสร็จ (ภาพซ้าย) และค่าฟังก์ชันแบ่งแยก (ภาพขวา). รูป 1.34 แสดงตัวอย่างของพฤติกรรมการจำแนกของแบบจำลอง เมื่อเลือกค่า \(C\) ต่าง ๆ. สังเกตุว่า ที่ค่า \(C\) ขนาดเล็ก จะเห็นขอบเขตของการแบ่งกว้าง และมีจุดข้อมูลล้ำแนวขอบเขตของการแบ่งจำนวนมาก. ที่ค่า \(C\) ขนาดใหญ่ ฟังก์ชันแบ่งแยกจะปรับการคำนวณ เพื่อให้จุดข้อมูลล้ำแนวขอบเขตของการแบ่งออกไปน้อยลง แต่ก็ทำให้ขอบเขตของการแบ่งแคบลง.
 |
 |
 |
 |
 |
 |
นอกจาก ซัพพอร์ตเวกเตอร์แมชชีนในรูปแบบดั้งเดิม ที่ระบุด้วยนิพจน์ \(\eqref{eq: svm dual}\) ยังมีรูปแบบที่พัฒนาขึ้นมาใหม่อีก เช่น นูซัพพอร์ตเวกเตอร์แมชชีน (\(\nu\)-SVM) ที่วางกรอบปัญหาเป็น \[\begin{eqnarray} \underset{\boldsymbol{\alpha}}{\mathrm{maximize}} & - \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j k(\boldsymbol{x}_i, \boldsymbol{x}_j) \nonumber \\ \mbox{s.t.} & \nonumber \\ & \begin{array}{ll} \sum_{i=1}^N \alpha_i y_i = 0, & \\ \sum_{i=1}^N \alpha_i \geq \nu , & \\ 0 \leq \alpha_i \leq 1/N & \mbox{ for } i =1, \ldots, N. \end{array} \label{eq: nu-svm} \end{eqnarray}\] โดย \(\nu\) เป็นอภิมานพารามิเตอร์ แทน \(C\) ในนิพจน์ \(\eqref{eq: svm dual}\).
4.2.2 ฟังก์ชันเคอร์เนล
ซัพพอร์ตเวกเตอร์แมชชีน จัดการการคำนวณอย่างสละสลวยที่ในการฝึก (นิพจน์ \(\eqref{eq: svm dual}\) และสมการ \(\eqref{eq: svm bo}\)) และการอนุมาน (สมการ \(\eqref{eq: svm discriminant function support vectors}\)) สามารถทำงานโดยตรงกับฟังก์ชันเคอร์เนล (kernel function) \(k(\boldsymbol{x}, \boldsymbol{x}')\) โดยไม่จำเป็นต้องอาศัยฟังก์ชันลักษณะสำคัญ \(\phi(\boldsymbol{x})\). โอกาสเช่นนี้ ทำให้การใช้งานซัพพอร์ตเวกเตอร์แมชชีน สามารถกำหนดฟังก์ชันเคอร์เนล ที่เทียบเท่าการทำงานในปริภูมิลักษณะสำคัญที่มีจำนวนมิติมาก ๆ ได้ โดยไม่จำเป็นต้องเข้าไปทำงานในปริภูมิที่มีมิติสูงนั้นโดยตรง. การใช้ประโยชน์แง่มุมนี้ มักถูกเรียกว่า ลูกเล่นเคอร์เนล (kernel tricks).
ฟังก์ชันเคอร์เนล อาจนิยมตรง ๆ จากฟังก์ชันลักษณะสำคัญด้วย \[\begin{eqnarray} k(\boldsymbol{x}, \boldsymbol{x}') &=& \phi(\boldsymbol{x})^T \phi(\boldsymbol{x}') = \sum_{m=1}^M \phi_m(\boldsymbol{x}) \phi_m(\boldsymbol{x}') \label{eq: kernel function} \end{eqnarray}\] เมื่อ \(\boldsymbol{x}\) และ \(\boldsymbol{x}'\) เป็นจุดข้อมูลสองจุด. ฟังก์ชัน \(\phi(\boldsymbol{x})\) เป็นฟังก์ชันลักษณะสำคัญ และ \(\phi_m(\boldsymbol{x})\) เป็นส่วนประกอบที่ \(m^{th}\) ของค่าฟังก์ชันลักษณะสำคัญ. ฟังก์ชันเคอร์เนล สามารถถูกออกแบบได้หลายวิธี. วิธีหนึ่ง (1) อาจกำหนดผ่านฟังก์ชันลักษณะสำคัญ และสมการ \(\eqref{eq: kernel function}\) อีกวิธีหนึ่งในการสร้างเคอร์เนล (2) อาจกำหนดฟังก์ชันเคอร์เนลโดยตรง โดยไม่ต้องอาศัยฟังก์ชันลักษณะสำคัญ แต่ต้องตรวจสอบว่าฟังก์ชันที่กำหนดนั้น มีคุณสมบัติเป็นฟังก์ชันเคอร์เนลได้. การตรวจสอบนั้น อาจจะใช้ทฤษฎีบทของเมอร์เซอร์ (Mercer’s theorem ดู สำหรับรายละเอียด) หรือ ใช้การตรวจแกรมเมทริกซ์ (Gram matrix) \(\boldsymbol{K} = [k_{ij}]\) สำหรับ \(i,j = 1, \ldots, N\) เมื่อ \(N\) เป็นจำนวนจุดข้อมูลฝึก (หรือจำนวนซัพพอร์ตเวกเตอร์) และ \(k_{ij} = k(\boldsymbol{x}_i, \boldsymbol{x}_j)\). ฟังก์ชันจะมีคุณสมบัติเป็นฟังก์ชันเคอร์เนลได้ หากแกรมเมทริกซ์เป็นเมทริกซ์บวกแน่นอน 5 (positive definite matrix) สำหรับทุก ๆ ค่าที่เป็นไปได้ของ \(\boldsymbol{x}\) และ \(\boldsymbol{x}'\).
แต่ (3) วิธีที่สะดวกกว่าในการสร้างฟังก์ชันเคอร์เนล คือสร้างจากฟังก์ชันเคอร์เนลที่ถูกตรวจสอบมาแล้ว ด้วยคุณสมบัติดังนี้ (จาก ). หาก \(k_1(\boldsymbol{x}, \boldsymbol{x}')\) และ \(k_2(\boldsymbol{x}, \boldsymbol{x}')\) มีคุณสมบัติเป็นฟังก์ชันเคอร์เนลได้แล้ว ฟังก์ชันต่อไปนี้ก็จะมีคุณสมบัติเป็นเคอร์เนลได้เช่นกัน \[\begin{eqnarray} k(\boldsymbol{x}, \boldsymbol{x}') &=& c k_1(\boldsymbol{x}, \boldsymbol{x}') \label{eq: kernel 1} \\ k(\boldsymbol{x}, \boldsymbol{x}') &=& f(\boldsymbol{x}) k_1(\boldsymbol{x}, \boldsymbol{x}') f(\boldsymbol{x}') \label{eq: kernel 2} \\ k(\boldsymbol{x}, \boldsymbol{x}') &=& \mathrm{polynomial}^+( k_1(\boldsymbol{x}, \boldsymbol{x}') ) \label{eq: kernel 3} \\ k(\boldsymbol{x}, \boldsymbol{x}') &=& \exp( k_1(\boldsymbol{x}, \boldsymbol{x}') ) \label{eq: kernel 4} \\ k(\boldsymbol{x}, \boldsymbol{x}') &=& k_1(\boldsymbol{x}, \boldsymbol{x}') + k_2(\boldsymbol{x}, \boldsymbol{x}') \label{eq: kernel 5} \\ k(\boldsymbol{x}, \boldsymbol{x}') &=& k_1(\boldsymbol{x}, \boldsymbol{x}') \cdot k_2(\boldsymbol{x}, \boldsymbol{x}') \label{eq: kernel 6} \\ k(\boldsymbol{x}, \boldsymbol{x}') &=& k_3(g(\boldsymbol{x}), g(\boldsymbol{x}')) \label{eq: kernel 7} \\ k(\boldsymbol{x}, \boldsymbol{x}') &=& \boldsymbol{x}^T \boldsymbol{A} \boldsymbol{x}' \label{eq: kernel 8} \\ k(\boldsymbol{x}, \boldsymbol{x}') &=& k_a(\boldsymbol{x}_a, \boldsymbol{x}'_a) + k_b(\boldsymbol{x}_b, \boldsymbol{x}'_b) \label{eq: kernel 9} \\ k(\boldsymbol{x}, \boldsymbol{x}') &=& k_a(\boldsymbol{x}_a, \boldsymbol{x}'_a) \cdot k_b(\boldsymbol{x}_b, \boldsymbol{x}'_b) \label{eq: kernel 10} \end{eqnarray}\] เมื่อ \(c > 0\) เป็นค่าคงที่. ฟังก์ชัน \(f: \mathbb{R}^D \mapsto \mathbb{R}\) เป็นฟังก์ชันใด ๆ. ฟังก์ชัน \(\mathrm{polynomial}^+\) เป็นฟังก์ชันพหุนามที่สัมประสิทธิ์ไม่มีค่าลบ. ฟังก์ชัน \(g: \mathbb{R}^D \mapsto \mathbb{R}^M\) และ \(k_3\) มีคุณสมบัติเป็นฟังก์ชันเคอร์เนลสำหรับ \(\mathbb{R}^M\). เมทริกซ์ \(\boldsymbol{A}\) สมมาตร และเป็นบวกกึ่งแน่นอน 6 เวกเตอร์ \(\boldsymbol{x}_a, \boldsymbol{x}'_a\) เป็นส่วนหน้าของ \(\boldsymbol{x}, \boldsymbol{x}'\) และเวกเตอร์ \(\boldsymbol{x}_b, \boldsymbol{x}'_b\) เป็นส่วนหน้าของ \(\boldsymbol{x}, \boldsymbol{x}'\) นั่นคือ \(\boldsymbol{x} = [\boldsymbol{x}_a, \boldsymbol{x}_b]^T\) และ \(k_a\) กับ \(k_b\) เป็นคุณสมบัติเป็นฟังก์ชันเคอร์เนลสำหรับปริภูมิย่อยดังกล่าว.
ฟังก์ชันเคอร์เนลที่นิยม และแนะนำสำหรับการเริ่มต้นใช้งานซัพพอร์ตเวกเตอร์แมชชีน ได้แก่ ฟังก์ชันเคอร์เนลเชิงเส้น และฟังก์ชันเคอร์เนลเกาส์เซียน.
ฟังก์ชันเคอร์เนลเชิงเส้น (linear kernel) ที่นิยามเป็น \[\begin{eqnarray} k(\boldsymbol{x}, \boldsymbol{x}') = \boldsymbol{x}^T \boldsymbol{x}' \label{eq: svm linear kernel} \end{eqnarray}\] ซึ่งคือ ฟังก์ชันลักษณะสำคัญเป็นฟังก์ชันเอกลักษณ์ \(\phi(\boldsymbol{x}) = \boldsymbol{x}\). ฟังก์ชันเคอร์เนลเชิงเส้น สร้างจากนิยามของเคอร์เนลในสมการ \(\eqref{eq: kernel function}\).
ฟังก์ชันเคอร์เนลเกาส์เซียน (Gaussian kernel) นิยามเป็น \[\begin{eqnarray} k(\boldsymbol{x}, \boldsymbol{x}') = \exp\left( -\frac{\|\boldsymbol{x} - \boldsymbol{x}'\|^2}{2 \sigma^2}\right) \label{eq: svm gaussian kernel} \end{eqnarray}\] ฟังก์ชันเคอร์เนลเกาส์เซียน อาจจะมองว่าสร้างมาจากคุณสมบัติของเคอร์เนล. พิจารณา \[\|\boldsymbol{x} - \boldsymbol{x}'\|^2 = \boldsymbol{x}^T \boldsymbol{x} - 2 \boldsymbol{x}^T \boldsymbol{x}' + (\boldsymbol{x}')^T \boldsymbol{x}'\] ซึ่งเท่ากับว่า \[k(\boldsymbol{x}, \boldsymbol{x}') = \exp \left(-\frac{1}{2 \sigma^2}\boldsymbol{x}^T \boldsymbol{x}\right) \cdot \exp \left(\frac{1}{\sigma^2} \boldsymbol{x}^T \boldsymbol{x}'\right) \cdot \exp \left(-\frac{1}{2 \sigma^2} (\boldsymbol{x}')^T \boldsymbol{x}'\right).\] นั่นคือ ใช้ฟังก์ชันเคอร์เนลเชิงเส้น \(\boldsymbol{x}^T \boldsymbol{x}'\) เป็นพื้นฐาน และใช้คุณสมบัติในสมการ \(\eqref{eq: kernel 2}\), \(\eqref{eq: kernel 4}\), และ \(\eqref{eq: kernel 1}\) ประกอบ.
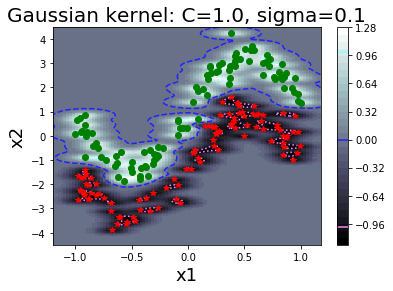
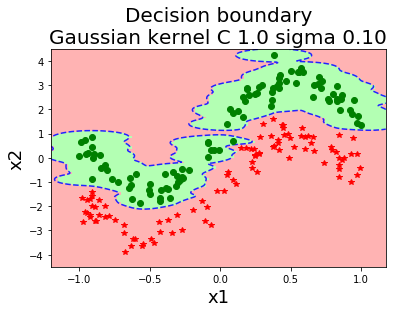
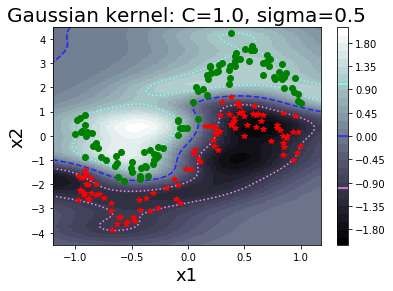
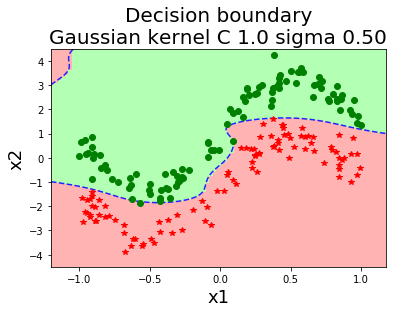
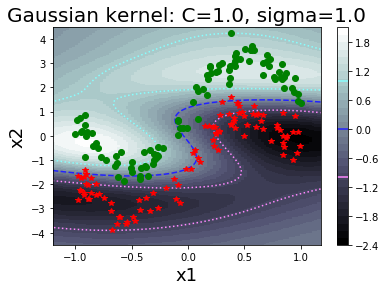
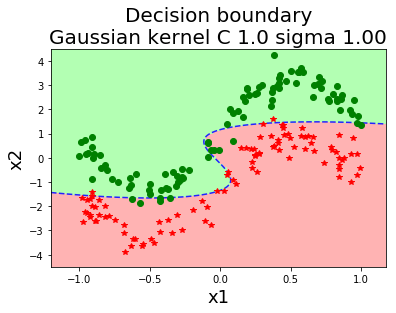
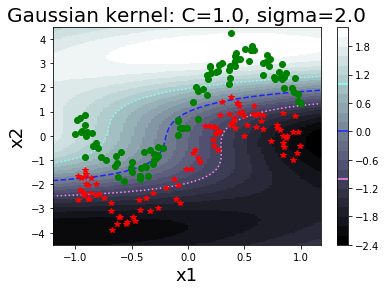
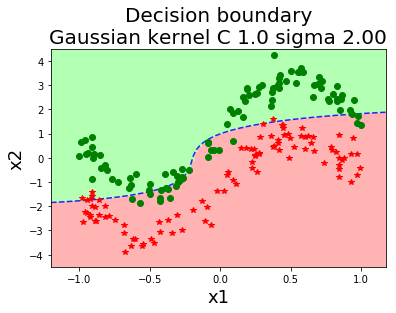
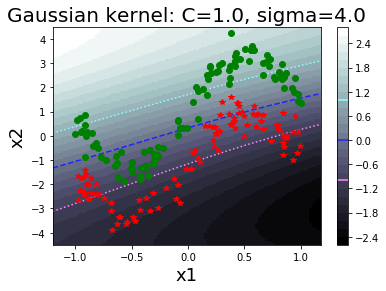
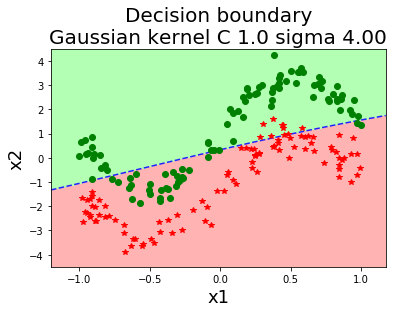
รูป 1.44 แสดงค่าฟังก์ชันแบ่งแยก เมื่อใช้ฟังก์ชันเคอร์เนลเกาส์เซียน ที่ค่า \(\sigma\) ต่าง ๆ. สังเกตุว่า ในภาพเส้นค่าค่าฟังก์ชันแบ่งแยกเป็นศูนย์ (ซึ่งสะท้อนถึงอภิระนาบในปริภูมิลักษณะสำคัญ) สามารถโค้งเลี้ยวไปตามข้อมูลได้ในปริภูมิข้อมูล. ภาพต่างทางขวา แสดงขอบเขตตัดสินใจ (decision boundary) ซึ่งเป็นส่วนในปริภูมิข้อมูล ที่ข้อมูลที่อยู่ภายในบริเวณจะถูกตัดสินตามชนิดของขอบเขตตัดสินใจ.
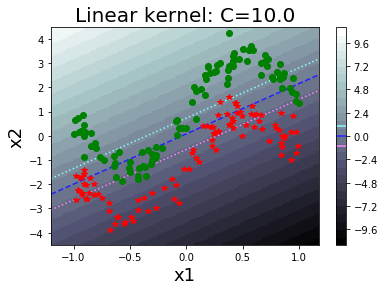
รูป 1.45 แสดงการใช้ฟังก์ชันเคอร์เนลเชิงเส้น เพื่อเปรียบเทียบ.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
4.3 อภิธานศัพท์
- การตรวจหาวัตถุ (object detection):
ภารกิจการหาตำแหน่งของวัตถุในภาพ หากภาพมีวัตถุอยู่.
- วิธีหน้าต่างเลื่อน (sliding window):
วิธีการเลือกส่วนภาพขนาดที่กำหนดจากข้อมูลภาพใหญ่ โดยการเลือกส่วนภาพ จะเลือกทั่วถึงจากทุกบริเวณในภาพใหญ่ ซึ่งอาจเริ่มจากมุมซ้ายบนของภาพใหญ่ เลือกส่วนภาพออกมา แล้วขยับไปทางขวา และทำเช่นนี้ไปจนสุดปลายด้านขวา แล้วจึงขยับลงล่างและไปเริ่มจากซ้ายสุด และทำลักษณะเช่นนี้อีก จนครอบคลุมบริเวณทั้งภาพใหญ่.
- ขนาดขยับเลื่อน (stride):
ขนาดของการเลื่อนหน้าต่างแต่ละครั้ง.
- การสกัดลักษณะสำคัญ (feature extraction):
การแปลงอินพุตดั้งเดิม ให้อยู่ในรูปแบบใหม่ โดยที่รูปแบบใหม่นี้จะช่วยให้ภาระกิจที่ต้องการดำเนินการได้สะดวกขึ้น.
- แบบจำลองแบ่งแยก (discriminative model):
แบบจำลองการจำแนกกลุ่ม ที่อาศัยหรือตีความได้ว่าใช้ความน่าจะเป็นภายหลัง \(\mathrm{Pr}(y|x)\) เมื่อ \(y\) เป็นค่ากลุ่มที่ต้องการทำนาย และ \(x\) เป็นอินพุตหรือตัวแปรต้น. ตัวอย่างเช่น โครงข่ายประสาทเทียม.
- แบบจำลองสร้างกำเนิด (generative model):
แบบจำลองการจำแนกกลุ่ม ที่อาศัยความน่าจะเป็น \(\mathrm{Pr}(x|y)\) ทางตรงหรือทางอ้อม เมื่อ \(x\) เป็นอินพุตหรือตัวแปรต้น และ \(y\) เป็นค่ากลุ่ม. โดยทั่วไปแล้ว \(x\) จะอยู่ในปริภูมิที่มีขนาดใหญ่กว่า \(y\) มาก ๆ เช่น ปัญหาการจำแนกภาพคน โดยเป็นภาพสเกลเทาขนาด \(H \times W\) ตัวแปร \(\boldsymbol{x}\) อยู่ในปริภูมิ \(\mathbb{R}^{H \times W}\) ในขณะที่ตัวแปร \(\boldsymbol{y}\) อยู่ในปริภูมิ \(\{+1, -1\}\).
- ฟังก์ชันแบ่งแยก (discriminant function):
แบบจำลองการจำแนกกลุ่ม ทำการคำนวณค่าเพื่อจำแนกกลุ่มโดยตรง ไม่อาศัยและไม่สามารถตีความในเชิงความน่าจะเป็น. ตัวอย่างเช่น ซัพพอร์ตเวกเตอร์แมชชีน.
- กล่องขอบเขต (bounding box):
บริเวณสี่เหลี่ยมที่เป็นขอบเขตภายในภาพ ซึ่งแต่ละกล่องขอบเขตสามารถระบุได้ด้วยสี่ค่า เช่น พิกัด \((x,y)\) มุมซ้ายบน และขนาดความกว้างกับความสูงของกล่อง \((w,h)\).
- การกำจัดการระบุซ้ำซ้อน (redundancy removal):
กลไกที่สำคัญสำหรับการตรวจจับภาพวัตถุ เพื่อกำจัดการระบุการตรวจพบตั้งแต่สองอันขึ้นไป ที่จริง ๆ แล้วระบุถึงวัตถุเดียวกัน.
- วิธีระงับค่าไม่มากสุดท้องถิ่น (non-local-maximum suppression):
วิธีหนึ่งในการกำจัดการระบุซ้ำซ้อน ที่ดำเนินการด้วยการตัดทิ้งกล่องขอบเขตที่มีค่าความเหมาะสมไม่มากที่สุด เมื่อเปรียบเทียบกับกล่องขอบเขตอื่น ๆ ที่อยู่รอบ ๆ กล่องนั้น โดย ค่าความเหมาะสม คือค่าที่ใช้วัดความมั่่นใจว่ากล่องขอบเขตนั้นมีวัตถุที่ค้นหาอยู่.
- ไอโอยู (IoU หรือ intersection of union):
ปริมาณวัด ที่วัดจากสัดส่วนพื้นที่ซ้อนทับกันของกล่องขอบเขตสองกล่อง ต่อพื้นที่รวม เพื่อบอกความใกล้เคียงของตำแหน่งการตรวจจับ อาจใช้ในกลไกของการตรวจจับ หรือใช้ในกระบวนการประเมินผล.
- วิธีการประมาณความหนาแน่นแก่น (kernel density estimation):
วิธีหนึ่งในการประมาณความหนาแน่นความน่าจะเป็นของข้อมูล.
- ค่าเฉลี่ยค่าประมาณความเที่ยงตรง (mean Average Precision หรือ mAP):
วิธีการวัดความสามารถของระบบตรวจจับภาพวัตถุ ที่คำนวณจากค่าประมาณพื้นที่ใต้กราฟของค่าความเที่ยงตรงและค่าระลึกกลับของวัตถุชนิดต่าง ๆ แล้วนำมาเฉลี่ยกัน.
- ปริภูมิลักษณะสำคัญ (feature space):
ปริภูมิหรือเซตของของค่าต่าง ๆ ที่เป็นไปได้ทั้งหมดของข้อมูล ในรูปแบบที่น่าจะช่วยให้ภาระกิจที่ต้องการทำได้ง่ายขึ้น.
- ซัพพอร์ตเวกเตอร์แมชชีน (support vector machine):
แบบจำลองจำแนกค่าทวิภาค ที่จำแนกข้อมูล ด้วยการใช้อภิระนาบในปริภูมิลักษณะสำคัญ. อภิระนาบที่ใช้ ถูกเลือกมาจากอภิระนาบที่สามารถแบ่งข้อมูลตัวอย่างได้ขอบเขตของการแบ่งกว้างที่สุด.
- อภิระนาบ (hyperplane):
ระนาบในปริภูมิหลายมิติ. สำหรับปริภูมิสองมิติ อภิระนาบคือเส้นตรง. สำหรับปริภูมิสามมิติ อภิระนาบคือแผ่นตรงเรียบ. ปริภูมิหลายมิติใด ๆ (กี่มิติก็ตาม) อภิระนาบสามารถบรรยายได้ด้วยสมการ \(\boldsymbol{w}^T \boldsymbol{x} + b = 0\) เมื่อ \(\boldsymbol{x}\) เป็นจุดใด ๆ ในปริภูมิ และ \(\boldsymbol{w}\) กับ \(b\) เป็นพารามิเตอร์ของอภิระนาบ.
- ขอบเขตของการแบ่ง (margin of separation):
ความห่างที่แบ่งกลุ่มข้อมูลสองกลุ่มออกจากกัน (ซึ่งอาจแบ่งได้สมบูรณ์ หรือไม่สมบูรณ์ก็ตาม).
- ขอบเขตตัดสินใจ (decision boundary):
บริเวณในปริภูมิข้อมูล ที่จุดข้อมูลต่าง ๆ หากอยู่ภายในบริเวณจะถูกจำแนกชนิดตามชนิดของขอบเขตตัดสินใจ.
- ซัพพอร์ตเวกเตอร์ (support vectors):
จุดข้อมูลที่สำคัญต่อการกำหนดอภิระนาบ.
- ลูกเล่นเคอร์เนล (kernel tricks):
การอาศัยรูปแบบการคำนวณของซัพพอร์ตเวกเตอร์แมชชีน ที่สามารถกำหนดฟังก์ชันเคอร์เนลได้โดยตรง และไม่ต้องกำหนดฟังก์ชันลักษณะสำคัญ.
- ฟังก์ชันเคอร์เนล (kernel function):
ฟังก์ชันคำนวณค่าสเกล่าร์ ที่บรรยายความสัมพันธ์ระหว่างจุดข้อมูลสองจุด. ในปริภูมิลักษณะสำคัญ.
- ฟังก์ชันเคอร์เนลเชิงเส้น (linear kernel):
ฟังก์ชันเคอร์เนล \(k(\boldsymbol{x}, \boldsymbol{x}) = \boldsymbol{x}^T \boldsymbol{x}'\).
- ฟังก์ชันเคอร์เนลเกาส์เซียน (gaussian kernel):
ฟังก์ชันเคอร์เนล \(k(\boldsymbol{x}, \boldsymbol{x}') = \exp\left( -\frac{\|\boldsymbol{x} - \boldsymbol{x}'\|^2}{2 \sigma^2}\right)\).