3 แบบฝึกหัด
“I learned that courage was not the absence of fear, but the triumph over it. The brave man is not he who does not feel afraid, but he who conquers that fear.”
—Nelson Mandela
“ผมได้เรียนรู้ว่า ความกล้าหาญไม่ใช่การปราศจากความกลัว แต่เป็นการเอาชนะความกลัว. คนกล้าหาญ ไม่ใช่คนที่ไม่รู้สึกกลัว แต่เป็นคนที่อยู่เหนือความกลัวนั้น.”
—เนลสัน แมนเดลา
3.0.0.0.1 แบบฝึกหัด
จากตัวอย่างการฝึกแบบจำลองพหุนามระดับขั้นหนึ่ง ในหัวข้อ [sec: curve fitting] จงเขียนรูปสมการในลักษณะเดียวกับสมการ \(\eqref{eq: polynomial M1}\) สำหรับแบบจำลองพหุนามระดับขั้นใด ๆ \(m\). คำใบ้ ลองทำสำหรับระดับขั้นสอง หรือระดับขั้นสามก่อน.
3.0.0.0.2 แบบฝึกหัด
จงแสดงให้เห็นว่าอนุพันธ์ของฟังก์ชันซิกมอยด์ คือ \[\begin{aligned} h'(a) & = z \cdot (1 - z) \label{eq: ann dsigmoid}\end{aligned}\] เมื่อ \(h'(a) = \frac{d h(a)}{d a}\) และ \(a\) คือผลรวมการกระตุ้น และ \(z\) คือผลลัพธ์จากการกระตุ้น นั่นคือ \(z = h(a)\).
3.0.0.0.3 แบบฝึกหัด
จงแสดงให้เห็นว่าอนุพันธ์ของฟังก์ชันไฮเปอร์บอลิกแทนเจนต์ \(\mathrm{tanh}(a) = (e^a - e^{-a})/(e^a + e^{-a})\) คือ \[\begin{aligned} \mathrm{tanh}'(a) & = 1 - z^2 \label{eq: ann dtanh} \end{aligned}\] เมื่อ \(\mathrm{tanh}'(a) = \frac{d \mathrm{tanh}(a)}{d a}\) และ \(a\) คือผลรวมการกระตุ้น และ \(z\) คือผลลัพธ์จากการกระตุ้น นั่นคือ \(z = \mathrm{tanh}(a)\).
3.0.0.0.4 แบบฝึกหัด
จงแสดงให้เห็นว่าอนุพันธ์ของฟังก์ชันเรเดียวเบซิส (radial basis function) \(r(a) = e^{-a^2}\) คือ \[\begin{aligned} r'(a) & = -2 a \cdot z \label{eq: ann dradial} \end{aligned}\] เมื่อ \(r'(a) = \frac{d r(a)}{d a}\) และ \(a\) คือผลรวมการกระตุ้น และ \(z\) คือผลลัพธ์จากการกระตุ้น นั่นคือ \(z = r(a)\).
3.0.0.0.5 แบบฝึกหัด
จงแสดงให้เห็นว่า \(\delta_k^{(L)} = \frac{\partial E}{\partial a_k^{(L)}} = \hat{y}_k - y_k\) สำหรับกรณีดังนี้
(ก) การหาค่าถดถอย ใช้ฟังก์ชันเอกลักษณ์ ซึ่งคือ \(\hat{y}_k = a^{(L)}_k\)
และฟังก์ชันจุดประสงค์ค่าผิดพลาดกำลังสอง คือ \(E = \frac{1}{2} \sum_k (\hat{y}_k - y_k)^2\).(ข) การจำแนกค่าทวิภาค ใช้ฟังก์ชันซิกมอยด์ ซึ่งคือ \(\hat{y}_k = \frac{1}{1 + \exp(-a^{(L)}_k)}\)
และฟังก์ชันจุดประสงค์ครอสเอนโทรปี \(E = - \sum_k \left\{ y_k \log (\hat{y}_k) + (1-y_k) \log (1-\hat{y}_k) \right\}\).(ค) การจำแนกกลุ่ม ใช้ฟังก์ชันซอฟต์แมกซ์ ซึ่งคือ \(\hat{y}_k = \frac{\exp(a^{(L)}_k)}{\sum_{j=1}^K \exp(a^{(L)}_j)}\)
และฟังก์ชันจุดประสงค์ครอสเอนโทรปี \(E = - \sum_j y_j \log (\hat{y}_j)\).
3.0.0.0.6 แบบฝึกหัด
การทำเรกูลาไรซ์ กล่าวง่าย ๆ คือการควบคุมพฤติกรรมการทำนายของแบบจำลอง เพื่อช่วยลดความเสี่ยงการโอเวอร์ฟิต โดยยังคงความซับซ้อนของแบบจำลองไว้. โครงข่ายประสาทเทียมสามารถทำเรกูลาไรซ์ได้ ดังเช่น ฟังก์ชันจุดประสงค์ ในสมการ \(\eqref{eq: ann En}\) สามารถถูกดัดแปลงเป็น \[\begin{eqnarray} \mathrm{loss}_n &=& E_n + \frac{\lambda}{2} \sum_q \sum_j \sum_i w_{ji}^2(q) \label{eq: ann regularized En} \end{eqnarray}\] เมื่อ \(w_{ji}(q) \equiv w_{ji}^{(q)}\) แทนค่าน้ำหนักในชั้น \(q^{th}\) ของแบบจำลอง. หมายเหตุ สัญลักษณ์ \(w_{ji}(q)\) ใช้แทน \(w_{ji}^{(q)}\) เพื่อลดความรุงรัง. จงแสดงให้เห็นว่า \[\begin{eqnarray} \frac{\partial \mathrm{loss}_n}{\partial w_{ji}^{(q)}} &=& \frac{\partial E_n}{\partial w_{ji}^{(q)}} + \lambda w_{ji}^{(q)} \label{eq: ann regularized derivative}. \end{eqnarray}\]
สังเกตว่า การทำเรกูลาไรซ์ไม่รวมค่าไบอัส.
3.1 แบบฝึกหัดเขียนโปรแกรม
3.1.0.0.1 แบบฝึกหัด
จากตัวอย่างการฝึกแบบจำลองพหุนามระดับขั้นหนึ่ง ในหัวข้อ [sec: curve fitting] โปรแกรมในรายการ [code: deg-1 poly example] แสดงตัวอย่างการปรับเส้นโค้งด้วยฟังก์ชันพหุนามระดับขั้นหนึ่ง. สามบรรทัดแรกเป็นการเตรียมข้อมูล. บรรทัดที่สี่ เป็นการฝึกแบบจำลอง ซึ่งเรียกใช้โปรแกรม train_poly1 ที่แสดงในรายการ [code: train deg-1 polynomial]. หลังจากฝึกแบบจำลองเรียบร้อย แบบจำลองที่ฝึกเสร็จ (แบบจำลองที่เลือก พร้อมค่าพารามิเตอร์ที่หามาได้) จะสามารถนำไปใช้งาน ซึ่งคือการทำนายคำตอบ จากค่าที่ถามได้ บรรทัดสุดท้าย แสดงตัวอย่างที่ทำนายค่า \(y\) สำหรับค่า \(x = 5\) ซึ่งทำโดยเรียกใช้ฟังก์ชัน fmodel ที่โปรแกรมแสดงในรายการ [code: polynomial model].
จงทำความเข้าใจโปรแกรมเหล่านี้ ทดสอบโปรแกรม และเปรียบเทียบผลกับตัวอย่างในหัวข้อ [sec: curve fitting].
def fmodel(x, w): # e.g., fmodel(5, [0.7, -0.65, 1])
w = np.array(w).reshape((-1,1))
m = len(w)
y = 0
for i in range(m):
y += w[i] * x**i
return ydef train_poly1(datax, datay):
N = datax.shape[0]
sumx, sumx2 = np.sum(datax), np.sum(datax**2)
sumy, sumyx = np.sum(datay), np.sum(datay*datax)
A = np.array([[N, sumx],[sumx, sumx2]])
b = np.array([[sumy],[sumyx]])
wt = np.linalg.solve(A, b)
return wtDX = [0.000, 0.111, 0.222, 0.333, 0.444, 0.556, 0.667, 0.778, 0.889, 1]
DY = [0.160, 0.724, 0.931, 0.712, 0.610, -0.460, -0.684, -1.299, -1.147, -0.045]
X, Y = np.array(DX), np.array(DY)
wo = train_poly1(X, Y); print('trained w =\n', wo)
print('Predict y = %.3f at x = 5'%fmodel(5, wo)) 3.1.0.0.2 แบบฝึกหัด
จากแบบฝึกหัด 1.0.0.0.1 และตัวอย่างโปรแกรมในแบบฝึกหัด 1.1.0.0.1 จงเขียนฟังก์ชัน train_poly ที่รับอาร์กิวเมนต์เป็นข้อมูล datax และ datay และระดับขั้นของฟังก์ชันพหุนาม M เพื่อฝึกแบบจำลองพหุนามระดับขั้น M.
3.1.0.0.3 แบบฝึกหัด
จากแบบฝึกหัด 1.1.0.0.2 จงเขียนโปรแกรม เพื่อศึกษาคุณสมบัติความทั่วไปของแบบจำลอง (หัวข้อ [sec: model selection]) โดยการสร้างข้อมูล \(y = \sin (2 \pi x) + \epsilon\) เมื่อ \(\epsilon \sim \mathcal{N}(0, 0.3)\) โดยสร้างข้อมูลขึ้นมา \(10\) จุดข้อมูลสำหรับการฝึก และ \(5\) จุดข้อมูลสำหรับการทดสอบ. ให้ \(x\) อยู่ในช่วง \(0\) ถึง \(1\). พร้อมเขียนโปรแกรม เพื่อวาดกราฟดังรูป [fig: multiple degs curve fitting with true nature] และ [fig: train and test data].
คำใบ้ ดูคำสั่ง np.linspace และ np.random.normal.
3.1.0.0.4 แบบฝึกหัด
รายการ [code: mlp] แสดงโปรแกรมคำนวณโครงข่ายประสาทเทียม. โปรแกรมคำนวณตามสมการ \(\eqref{eq: mlp feedforward a vec}\) และ \(\eqref{eq: mlp feedforward z vec}\). โดยรับ จำนวนชั้นคำนวณ ผ่าน net_params['layers']. ค่าของพารามิเตอร์ต่าง ๆ ก็รับผ่าน net_params เช่น ค่าไบอัสชั้นที่หนึ่ง ผ่าน net_params['bias1'] ค่าน้ำหนักชั้นที่หนึ่ง ผ่าน net_params['weight1'] โดยตัวเลขตามหลังชื่อระบุชั้นของพารามิเตอร์. ค่าไบอัส เป็นเวกเตอร์ที่มีจำนวนส่วนประกอบเท่ากับจำนวนโหนดในชั้นคำนวณ. ค่าน้ำหนัก เป็นเมทริกซ์ขนาด \(M_q \times M_{q-1}\) เมื่อ \(M_q\) คือจำนวนโหนดของชั้นคำนวณ และ \(M_{q-1}\) คือจำนวนโหนดของชั้นคำนวณก่อนหน้า. เพื่อความสะดวกในการเขีียนโปรแกรม อินพุตถูกกำหนด เป็นเสมือนเอาต์พุตจากชั้นคำนวณที่ศูนย์. อินพุต X ที่รับเข้าต้องอยู่ในรูปเมทริกซ์ ขนาด \(D \times N\) เมื่อ \(D\) เป็นจำนวนมิติของอินพุต และ \(N\) เป็นจำนวนจุดข้อมูล. โครงข่ายประสาทเทียมจะให้เอาต์พุตออกมา ในรูปเมทริกซ์ ขนาด \(K \times N\) เมื่อ \(K\) คือจำนวนมิติของเอาต์พุตที่ต้องการ.
การกำหนดจำนวนโหนดในแต่ละชั้นคำนวณ ทำทางอ้อมผ่านการกำหนดขนาดของค่าไบอัส และขนาดของค่าน้ำหนัก. นอกจากจำนวนชั้นคำนวณ ค่าไบอัส และค่าน้ำหนักแล้ว ฟังก์ชันกระตุ้นสามารถกำหนดได้ในแต่ละชั้นคำนวณ เช่น หากกำหนดฟังก์ชันกระตุ้นของชั้นคำนวณที่หนึ่ง เป็นฟังก์ชันจำกัดแข็ง อาจทำโดย การกำหนดค่า net_params['act1'] ให้เป็น hardlimit เมื่อ hardlimit อ้างถึงฟังก์ชันจำกัดแข็งที่โปรแกรมแสดงในรายการ [code: hardlimit].
ข้อสังเกต ฟังก์ชัน hardlimit ไม่ได้เขียนโดยใช้คำสั่ง if. อะไรคือข้อดีข้อเสีย ของการเขียนโปรแกรมในแบบรายการ [code: hardlimit] เปรียบเทียบกับการเขียนโดยใช้คำสั่ง if
def mlp(net_params, X):
assert X.shape[0] == net_params['weight1'].shape[1], 'X: D,N'
num_layers = net_params['layers']
# Feed forward
Z = X
for i in range(1, num_layers):
b = net_params['bias%d'%i]
w = net_params['weight%d'%i]
act_f = net_params['act%d'%i]
A = np.dot(w, Z) + b # A: M x N
Z = act_f(A) # Z: M x N
return Z # M x Ndef hardlimit(a):
return 1*(a > 0)การใช้งานโปรแกรมคำนวณโครงข่ายประสาทเทียม สามารถทำได้ เช่น หากทำการคำนวณตรรกะเอ็กซ์ออร์ ในรูป [fig: ANN MLP for XOR] การคำนวณสามารถทำได้ดังแสดงในรายการ [code: xor]. ตัวแปร net กำหนดจำนวนชั้นคำนวณ ค่าน้ำหนัก ค่าไบอัส และฟังก์ชันกระตุ้น.
จงศึกษาโปรแกรมเหล่านี้ ทดลองรัน และปรังแต่งโครงข่ายประสาทเทียม โดยใช้ค่าน้ำหนักและค่าไบอัสอื่น หรือปรับแต่งเป็นโครงสร้างอื่น สังเกตผล และสรุป. หมายเหตุ โครงข่ายในรูป [fig: ANN MLP for XOR] เป็นโครงข่ายสองชั้น แต่การเรียกใช้โปรแกรม mlp กำหนด 'layers': 3 ซึ่งในโปรแกรม mlp นับอินพุตเป็นชั้นคำนวณที่ศูนย์เข้าไปด้วย โดยชั้นคำนวณที่ศูนย์ไม่มีการคำนวณ (ใช้ Z = X แล้วเริ่มคำนวณลูปจากดัชนีที่หนึ่ง ดูรายการ [code: mlp] ประกอบ).
net = {'layers': 3, 'bias1': np.array([[-20],[-20]]),
'weight1': np.array([[-30, 30],[30, -30]]),
'bias2': np.array([[-20]]), 'weight2': np.array([[30, 30]]),
'act1': hardlimit, 'act2': hardlimit}
x = np.array([[0, 0, 1, 1], [0, 1, 0, 1]])
y = mlp(net, x)
print(x[0,:])
print(x[1,:])
print(y[0,:])3.1.0.0.5 แบบฝึกหัด
รายการ [code: train_mlp] แสดงโปรแกรมฝึกโครงข่ายประสาทเทียม train_mlp ที่ใช้วิธีแพร่กระจายย้อนกลับ คำนวณค่าเกรเดียนต์ และใช้วิธีลงชันที่สุด เพื่อปรับค่าพารามิเตอร์. การปรับค่าพารามิเตอร์ใช้ข้อมูลฝึกทุกจุดทีเดียว และการปรับทำครั้งเดียวในแต่ละสมัยฝึก นี่คือ การฝึกแบบหมู่. โปรแกรม train_mlp รับแบบจำลอง (พร้อมค่าพารามิเตอร์เริ่มต้น) ผ่านอาร์กิวเมนต์ net_params ซึ่งเป็นไพธอนดิกชันนารีที่มีกุญแจต่าง ๆ ดังอภิปรายในแบบฝึกหัด 1.1.0.0.4. อาร์กิวเมนต์ trainX และ trainY เป็นตัวแปรต้น และตัวแปรตามของข้อมูลฝึก ที่อยู่ในรูป \(D \times N\) และ \(K \times N\) ตามลำดับ เมื่อ \(D\), \(K\), และ \(N\) เป็นจำนวนมิติของอินพุต จำนวนมิติของเอาต์พุต และจำนวนจุดข้อมูล ตามลำดับ. อาร์กิวเมนต์ loss อ้างถึงฟังก์ชันสูญเสีย ที่จะใช้เป็นฟังก์ชันจุดประสงค์. อาร์กิวเมนต์ lr แทนอัตราการเรียนรู้. อาร์กิวเมนต์ epochs แทนจำนวนสมัยที่จะฝึก.
โปรแกรม train_mlp รีเทิร์นไพธอนดิกชันนารี net_params ที่แทนโครงสร้างแบบจำลอง ซึ่งค่าพารามิเตอร์ได้ถูกปรับเปลี่ยนไปแล้ว จากการฝึก และรีเทิร์นไพธอนลิสต์ train_losses ที่บันทึกค่าเฉลี่ยค่าผิดพลาดกำลังสองของแบบจำลองหลังฝึกแต่ละสมัย. สังเกต ขั้นตอนที่สามของการแพร่กระจายย้อนกลับ ในโปรแกรมใช้ delta[i - 1] = dsigmoid(Z[i - 1]) * sumdw ซึ่งเรียกใช้อนุพันธ์ของซิกมอยด์ ดังนั้น หากชั้นซ่อนใช้ฟังก์ชันกระตุ้นอื่น นอกจากซิกมอยด์ จะต้องแก้ไขโปรแกรมที่ส่วนนี้. ในเบื้องต้นนี้ โปรแกรมใช้คำสั่ง assert act_f == sigmoid เพื่อป้องกัน ความพลั้งเผลอที่อาจเกิดขึ้น.
def train_mlp(net_params, trainX, trainY, loss, lr=0.1,
epochs=1000):
# '''
# net_params
# * 'layers': number of layers, inc. input layer.
# * 'bias1': bias of layer 1.
# * 'weight1': weight of layer 1.
# * 'act1': activation function of layer 1.
# * ...
# loss: loss function with interface loss(yp, y).
# lr: learning rate.
# epochs: number of training epochs.
# '''
num_layers = net_params['layers']
last_layer = num_layers-1
out_act = 'act%d'%last_layer
_, N = trainX.shape
A = {}
Z = {0: trainX}
delta = {}
dEw = {}
dEb = {}
train_losses = []
step_size = lr/N
for nt in range(epochs):
# (1) Forward pass
for i in range(1, num_layers):
b = net_params['bias%d'%i]
w = net_params['weight%d'%i]
act_f = net_params['act%d'%i]
A[i] = np.dot(w, Z[i-1]) + b # A: M x N
Z[i] = act_f(A[i]) # Z: M x N
# end forward pass
Yp = Z[i]
# (2) Calculate output dE/da
delta[last_layer] = Yp - trainY # delta: M x N
# (3) Backpropagate to calculate dE/da for layer i-1
for i in range(last_layer, 1, -1):
b = net_params['bias%d'%i] # b: Mnext x 1
w = net_params['weight%d'%i] # w: Mnext x M
act_f = net_params['act%d'%(i-1)]
sumdw = np.dot(w.transpose(), delta[i]) # M x N
assert act_f == sigmoid
delta[i - 1] = dsigmoid(Z[i - 1]) * sumdw # M x N
# (4) Calculate gradient dE/dw and dE/db
dEw[i] = np.dot(delta[i], Z[i-1].transpose()) #Mnxt,M
dEb[i] = np.dot(delta[i], np.ones((N, 1))) #Mnxt,1
# end backpropagate
# Calculate gradient dE/dw and dE/db: dE ~ d sum En
dEw[1] = np.dot(delta[1], Z[0].transpose()) # M1 x M0
dEb[1] = np.dot(delta[1], np.ones((N, 1))) # M1 x 1
# Update parameters w/ Gradient Descent
for i in range(1, num_layers):
b = net_params['bias%d'%i]
w = net_params['weight%d'%i]
b -= step_size * dEb[i]
w -= step_size * dEw[i]
# end update parameters
# Calculate loss at each epoch
lossn = np.sum(loss(Yp, trainY), axis=0)
train_losses.append(np.mean(lossn)) # loss = MSE
# end epoch nt
return net_params, train_lossesรายการ [code: sigmoid] แสดงโปรแกรมคำนวณฟังก์ชันซิกมอยด์และอนุพันธ์. สังเกตว่า อนุพันธ์ของซิกมอยด์ รับอาร์กิวเมนต์ที่เป็นผลลัพธ์จากการกระตุ้นแล้ว \(\boldsymbol{Z}\) ไม่ใช่ผลรวมการกระตุ้น \(\boldsymbol{A}\). (ดูแบบฝึกหัด 1.0.0.0.2 และอภิปรายถึงข้อดีข้อเสียของการเขียนโปรแกรมให้รับอาร์กิวเมนต์เป็น \(\boldsymbol{Z}\) เปรียบเทียบกับการเขียนโปรแกรมให้รับอาร์กิวเมนต์เป็น \(\boldsymbol{A}\). คำใบ้ โปรแกรมที่มีประสิทธิภาพ ควรลดการคำนวณที่ซ้ำซ้อน.)
รายการ [code: identity] แสดงโปรแกรมคำนวณฟังก์ชันเอกลักษณ์ ซึ่งทำหน้าที่ เป็นจุดอ้างอิง เพื่อให้โปรแกรม mlp และ train_mlp รวมถึงการปรับแต่งโครงข่ายประสาทเทียม ผ่านไพธอนดิกชันนารี net_params ทำได้สะดวก และยืดหยุ่น.
def sigmoid(a):
return 1/(1 + np.exp(-a))
def dsigmoid(z): # Caution!: argument is z, not a!
return z * (1 - z)def identity(a):
return aรายการ [code: w_initn] แสดงโปรแกรมกำหนดค่าน้ำหนักเริ่มต้นด้วยการสุ่ม. โปรแกรม w_initn สุ่มค่าไบอัสและค่าน้ำหนัก จากการแจกแจงเกาส์เซียน ซึ่งค่าดีฟอลต์คือค่าเฉลี่ยเป็น \(0\) และค่าเบี่ยงเบนมาตราฐานเป็น \(1\). โปรแกรมรับอาร์กิวเมนต์ Ms เป็นลิสต์ของเลขที่ระบุจำนวนโหนดในแต่ละชั้น โดยเริ่มจากจำนวนโหนดในชั้นอินพุต (ซึ่งคือจำนวนมิติของอินพุต) และตามด้วยจำนวนโหนดในชั้นคำนวณที่หนึ่ง จนถึงจำนวนโหนดในชั้นเอาต์พุต (ซึ่งเท่ากับจำนวนมิติของเอาต์พุตสุดท้าย). โปรแกรมรีเทิร์นไพธอนดิกชันนารี ในรูปแบบของโครงข่ายประสาทเทียม ที่จะสามารถใช้ได้กับ mlp (รายการ [code: mlp]) และ train_mlp (รายการ [code: train_mlp]) ถ้าเพิ่มค่าของฟังก์ชันกระตุ้นเข้าไป.
def w_initn(Ms, umeansigma=(0,1)):
assert len(Ms) >= 2, 'Ms: list of units in each layer'
num_layers = len(Ms)
params = {'layers': num_layers}
mu = umeansigma[0]
sigma = umeansigma[1]
for i, m in enumerate(Ms[1:], start=1):
mprev = Ms[i-1]
b = np.random.randn(m,1)
w = np.random.randn(m, mprev)
params['bias%d'%i] = b*sigma + mu
params['weight%d'%i] = w*sigma + mu
return paramsรายการ [code: sqr_error] แสดงโปรแกรมคำนวณค่าผิดพลาดกำลังสอง ซึ่งใช้ช่วยประเมินการฝึก.
def sqr_error(yhat, y):
assert yhat.shape == y.shape
return (yhat - y)**2 # output: K x Nจากโปรแกรมต่าง ๆ ที่มี ตัวอย่างต่อไปนี้แสดง การสร้าง การฝึก และใช้แบบจำลองที่ฝึกแล้วในการทำนาย. สมมติ ข้อมูลจำนวน \(200\) จุดข้อมูล ทั้งตัวแปรต้นและตัวแปรตามมีมิติเดียว ได้มาดังนี้
x = np.linspace(0, 1, 200)
noise = np.random.rand(200)
y = x + 0.3 * np.sin(2 * np.pi * x) + 0.1 * noise
x, y = x.reshape((1, -1)), y.reshape((1, -1))สมมติต้องการใช้โครงข่ายประสาทเทียมสองชั้น ขนาด \(8\) หน่วยซ่อน โครงข่ายประสาทเทียมสามารถถูกสร้าง และฝึกได้ดังนี้
net = w_initn([1, 8, 1])
net['act1'] = sigmoid
net['act2'] = identity
tnet, losses = train_mlp(net, x, y, sqr_error, lr=0.3, epochs=40000)เมื่อ เลือกใช้อัตราเรียนรู้ \(0.3\) และทำการฝึก \(40000\) สมัย. ผลลัพธ์ที่ได้คือ แบบจำลองที่ฝึกแล้ว tnet และความก้าวหน้าในการฝึก losses. การฝึกทุกครั้งควรตรวจสอบความก้าวหน้าในการฝึก ว่าดำเนินไปได้ด้วยดี เช่น ทำ plt.plot(losses) เพื่อดูว่ากราฟลู่ลงจนราบดีแล้ว. หลังจากฝึกเสร็จแล้ว แบบจำลอง tnet สามารถนำไปใช้ทำนายได้ เช่น Yp = mlp(tnet, x) เมื่อ x เป็นตัวแปรต้นที่ถาม และผลลัพธ์การทำนายคือ Yp.
จงศึกษาโปรแกรมเหล่านี้ ทดลองสร้าง ทดลองฝึก และทดลองใช้แบบจำลองทำนาย รวมไปถึงประเมินผลการทำนาย เช่น ลองวัดค่ารากที่สองของค่าเฉลี่ยค่าผิดพลาดกำลังสอง np.sqrt(np.mean( sqr_error(Yp, y))) และลองวาดผลการทำนาย เปรียบเทียบกับข้อมูล เช่น
plt.plot(x[0], y[0], 'r*', label='Ground Truth')
plt.plot(x[0], Yp[0], 'go', label='ANN')อภิปราย และสรุปสิ่งที่ได้เรียนรู้.
3.1.0.0.6 แบบฝึกหัด
การกำหนดค่าน้ำหนักเริ่มต้น มีผลอย่างมากต่อการฝึกโครงข่ายประสาทเทียม. จงสร้างข้อมูล (ดูแบบฝึกหัด 1.1.0.0.5) แบ่งข้อมูลออกเป็นข้อมูลฝึก และข้อมูลทดสอบ. จากนั้น เลือกโครงข่ายประสาทเทียมที่เหมาะสม แล้วทดลองฝึกโครงข่ายประสาทเทียม และวัดผลการทำงานกับข้อมูลทดสอบ. ทดลองซ้ำทั้งหมดไม่น้อยกว่า \(40\) ซ้ำ ซึ่งในแต่ละซ้ำ ทำการกำหนดค่าน้ำหนักเริ่มต้นใหม่ทุกครั้ง นอกนั้นให้ทำอย่างอื่นเหมือนเดิม. การกำหนดค่าน้ำหนักเริ่มต้น ให้ใช้วิธีการสุ่ม (รายการ [code: w_initn]) สังเกตผลการทำงานจากการทดลองซ้ำ อภิปรายผล และทำการทดลองเช่นนี้อีก แต่ใช้วิธีเหงี่ยนวิดโดรว์ (รายการ [code: w_initngw]) ในการกำหนดค่าน้ำหนักเริ่มต้น เปรียบเทียบผลที่ได้ อภิปราย และสรุปสิ่งที่ได้เรียนรู้.
หมายเหตุ การแบ่งข้อมูล อาจทำได้ดังนี้ เมื่อ x และ y เป็นตัวแปรต้นและตัวแปรตามของข้อมูล ซึ่งมีจำนวน N จุดข้อมูล. ในตัวอย่างแบ่งข้อมูล โดยแบ่งให้ประมาณ \(60\%\) ของข้อมูลทั้งหมดใช้เป็นข้อมูลฝึก (trainx และ trainy) และที่เหลือเป็นข้อมูลทดสอบ (testx และ testy).
_, N = x.shape
ids = np.random.choice(N, N, replace=False)
train_size = 0.6
mark = round(train_size*N)
train_ids = ids[:mark]
test_ids = ids[mark:]
trainx, trainy = x[:, train_ids], y[:, train_ids]
testx, testy = x[:, test_ids], y[:, test_ids]หากแบ่งข้อมูลดังคำสั่งข้างต้นแล้ว การฝึกแบบจำลอง การใช้แบบจำลองทำนายข้อมูลทดสอบ และวัดผลการทดสอบด้วยค่ารากที่สองของค่าเฉลี่ยค่าผิดพลาดกำลังสอง (rmse) สามารถทำได้ดังเช่น
tnet, losses = train_mlp(net, trainx, trainy, sqr_error, 0.3, 40000)
Yp = mlp(trained_net, testx)
rmse = np.sqrt(np.mean(sqr_error(Yp, testy)))def w_initngw(Ms, maxoff=(1.4, 0)):
assert len(Ms) >= 2
num_layers = len(Ms)
params = {'layers': num_layers}
scale = maxoff[0]
offset = maxoff[1]
for i, m in enumerate(Ms[1:], start=1):
mprev = Ms[i-1]
wmax = scale*m**(1/mprev)
wi_ = np.random.rand(m, mprev) * 2 - 1
denomi = np.sqrt(np.sum(wi_**2, axis=1).reshape((-1,1)))
wi = wmax * wi_ /denomi
bi = wmax * np.linspace(-1, 1, m) \
* np.sign(np.random.rand(m)) + offset
params['bias%d'%i] = bi.reshape((m,1))
params['weight%d'%i] = wi
return params รูป 1 และ 2 แสดงตัวอย่างผลจากการทดลอง ซึ่งเลือกผลที่ดีที่สุด (ค่าผิดพลาดทดสอบต่ำสุด) จากการทดลองซ้ำ \(40\) ครั้ง เมื่อกำหนดค่าน้ำหนักเริ่มต้น ด้วยการสุ่ม และด้วยวิธีเหงี่ยนวิดโดรว์ ตามที่ระบุในคำบรรยายรูป.
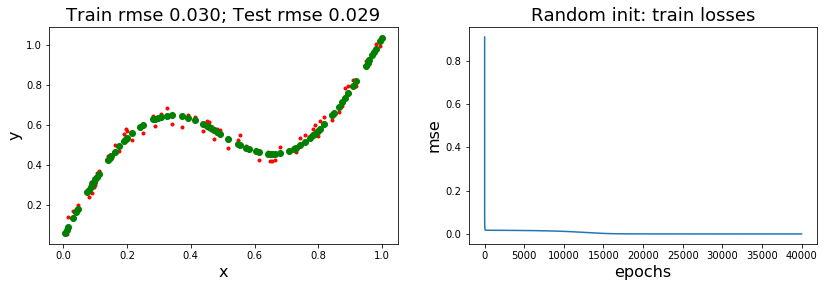
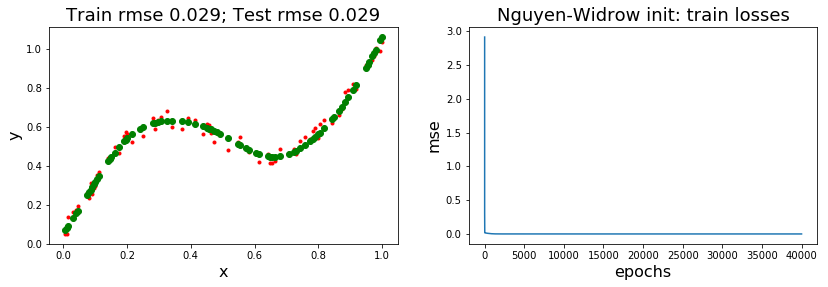
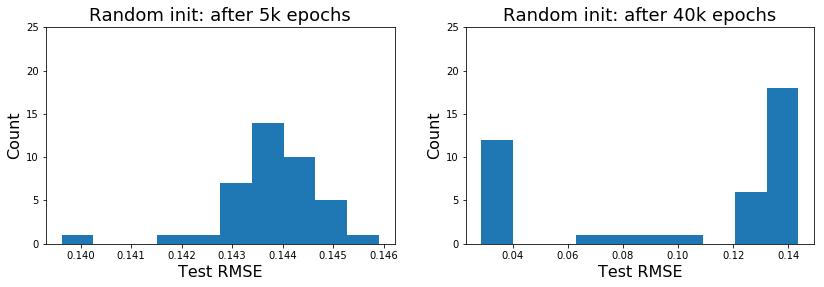
รูป 4 และ 5 แสดงตัวอย่างวิธีการนำเสนอผลศึกษา. ตาราง 1 แสดงตัวอย่างค่าสถิติจากการศึกษา. สังเกตจากผลในตัวอย่าง ผลการทำงานของแบบจำลองที่ฝึกแล้ว เมื่อใช้การสุ่มกำหนดค่าเริ่มต้น จะมีความหลากหลายค่อนข้างมาก. เมื่อเปรียบเทียบกับวิธีเหงี่ยนวิดโดรว์ (1) ผลลัพธ์ที่ดีที่สุด เมื่อกำหนดค่าเริ่มต้นด้วยวิธีสุ่ม หากฝึกนานพอ ไม่ได้ต่างจาก ผลลัพธ์ที่ดีที่สุด เมื่อกำหนดค่าเริ่มต้นด้วยวิธีเหงี่ยนวิดโดรว์. แต่ (2) การกำหนดค่าเริ่มต้นด้วยวิธีเหงี่ยนวิดโดรว์ สามารถช่วยให้ได้แบบจำลองที่ดี โดยใช้จำนวนสมัยฝึกที่น้อยกว่า การกำหนดค่าเริ่มต้นด้วยวิธีสุ่ม. (3) ผลลัพธ์โดยเฉลี่ย ของการกำหนดค่าเริ่มต้นด้วยวิธีเหงี่ยนวิดโดรว์ ดีกว่า ผลลัพธ์โดยเฉลี่ย เมื่อกำหนดค่าเริ่มต้นด้วยวิธีสุ่ม. (4) โอกาสที่จะได้แบบจำลองที่ดี เมื่อกำหนดค่าเริ่มต้นด้วยวิธีเหงี่ยนวิดโดรว์ จะสูงกว่าเมื่อกำหนดค่าเริ่มต้นด้วยวิธีสุ่ม ถึงสองเท่าครึ่ง หากฝึกนานพอ.
ที่ \(40000\) สมัย นับค่าผิดพลาดน้อยกว่า \(0.04\) ได้ \(12\) ครั้งจาก \(40\) ครั้ง หรือคิดเป็น มีโอกาสประมาณ \(30\%\) เมื่อใช้วิธีสุ่ม และฝึกนานพอ เปรียบเทียบกับ ประมาณ \(95\%\) (นับได้ \(38\) ครั้ง) เมื่อใช้วิธีเหงี่ยนวิดโดรว์. แต่ที่ \(5000\) สมัย ค่าผิดพลาดที่ต่ำกว่า \(0.04\) ไม่มีเลย เมื่อใช้วิธีสุ่ม เปรียบเทียบกับ มีโอกาสประมาณ \(80\%\) (นับได้ \(32\) ครั้ง) เมื่อใช้วิธีเหงี่ยนวิดโดรว์. เปรียบเทียบผลที่ได้ทำการทดลองเอง กับผลตัวอย่างที่นำเสนอในรูป 4 และตาราง 1 อภิปรายผลที่ได้ กับข้อสังเกตที่ตั้งไว้นี้ รวมถึงอภิปรายถึงแนวทางปฏิบัติ เมื่อทำแบบจำลองโครงข่ายประสาทเทียม.
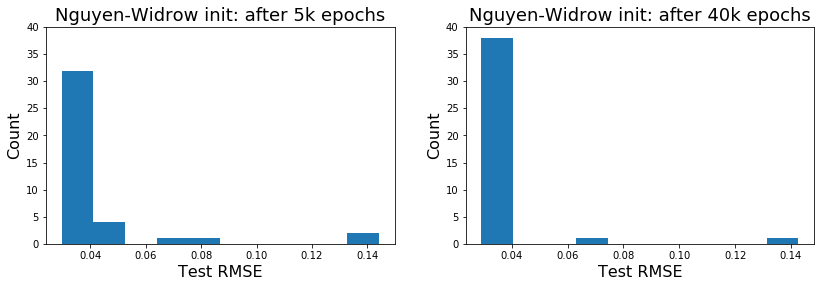
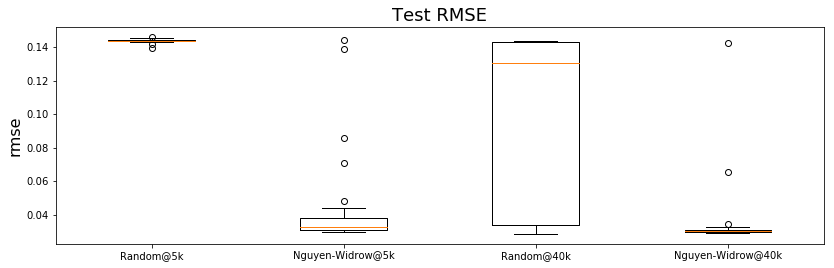
| ผลจากแบบจำลองที่ผ่านการฝึก | |||
| การกำหนดค่าน้ำหนักเริ่มต้น | ค่าสถิติ | \(5000\) สมัย | \(40000\) สมัย |
| ค่าน้อยที่สุด | \(0.140\) | \(0.029\) | |
| วิธีสุ่ม | ค่าเฉลี่ย | \(0.144\) | \(0.101\) |
| ค่ามากที่สุด | \(0.146\) | \(0.144\) | |
| ค่าน้อยที่สุด | \(0.030\) | \(0.029\) | |
| วิธีเหงี่ยนวิดโดรว์ | ค่าเฉลี่ย | \(0.041\) | \(0.034\) |
| ค่ามากที่สุด | \(0.144\) | \(0.143\) | |
3.1.0.1 ความสำคัญของการทำซ้ำ.
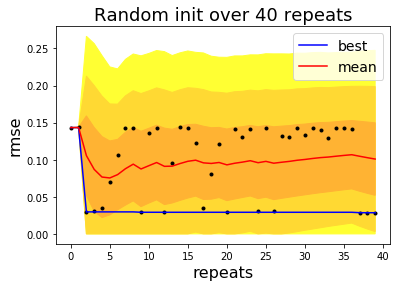
เกี่ยวกับการทำซ้ำ การทำแบบจำลองด้วยโครงข่ายประสาทเทียม นิยมทำซ้ำหลายครั้ง (หากทรัพยากรอำนวย) เนื่องจาก ผลค่อนข้างจะหลากหลาย ดังที่เห็นจากรูป 4 โดยเฉพาะอย่างยิ่งเมื่อใช้วิธีการกำหนดค่าน้ำหนักเริ่มต้นด้วยการสุ่ม. รูป 6 แสดงความสำคัญของการทำซ้ำ ซึ่งช่วยให้มีโอกาสมากพอ ที่จะพบแบบจำลองที่ดี หรืออย่างน้อย ก็ช่วยให้ได้เห็นความสามารถโดยเฉลี่ยของแบบจำลองและการฝึกที่ใช้.
โปรแกรมข้างล่างนี้ เป็นตัวอย่างคำสั่งส่วนหนึ่ง (ไม่ใช่ทั้งหมด) ที่ใช้สร้างรูป 6.
cave = []
cstd = []
cbest = []
for i in range(40):
cave.append(np.mean(trmses[:(i+1)]))
cstd.append(np.std(trmses[:(i+1)]))
cbest.append(np.min(trmses[:(i+1)]))
cave = np.array(cave)
cstd = np.array(cstd)
cbest = np.array(cbest)
ci_u = cave + cstd
ci_l = cave - cstd
ci_ys = np.hstack( (ci_u, ci_l[::-1]) )
plt.fill(ci_xs, ci_ys, color=(1, 0.7, 0.2))
plt.plot(trmses, 'k.')
plt.plot(cbest, color=(0, 0, 1), label='best')
plt.plot(cave, 'r-', label='mean')เมื่อ trmses แทนไพธอนลิสต์ที่เก็บค่าผิดพลาดทดสอบของแต่ละซ้ำไว้ ทั้งหมด \(40\) ซ้ำ. หมายเหตุ ค่าสถิติที่ใช้ทำ แถบความเชื่อมั่น (confidence intervals) ในรูป คือ \(\mu \pm \sigma\) (แสดงในโปรแกรมตัวอย่างข้างต้น) และ \(\mu \pm 2 \sigma\) กับ \(\mu \pm 3 \sigma\) (ไม่ได้แสดงในโปรแกรมตัวอย่าง). สังเกตว่า แนวทางปฏิบัติ ที่ทำซ้ำหลาย ๆ ครั้ง และเลือกแบบจำลองที่ทำงานได้ดีที่สุด นั้น เป็นเสมือนการหาค่าดีที่สุดอ่อน ๆ (soft optimization) ที่ช่วยบรรเทา การติดกับสถานการณ์ที่ดีที่สุดท้องถิ่น ของขั้นตอนวิธีหาค่าดีที่สุดลงได้บ้าง.
3.1.0.1.1 แบบฝึกหัด
จากรูป [fig: ann normalizaton motivation] จงสร้างข้อมูลชุดบี จากความสัมพันธ์ \(y = 0.1 (x - 100) + 0.3 \sin( 0.2 \pi (x - 100) ) + \epsilon\) เมื่อ \(\epsilon \sim \mathcal{U}(0,1)\). สัญกรณ์ \(\epsilon \sim \mathcal{U}(0,1)\) หมายถึง ค่าของ \(\epsilon\) สุ่มจากการแจกแจงเอกรูป. สร้างข้อมูลขึ้นมา \(500\) จุดข้อมูลสำหรับการฝึก และ \(250\) จุดข้อมูลสำหรับการทดสอบ. ให้ \(x\) อยู่ในช่วง \(100\) ถึง \(110\). ทดลองใช้โครงข่ายประสาทเทียมสองชั้น ที่มีจำนวนหน่วยซ่อน \(8\) หน่วย เลือกอภิมานพารามิเตอร์ เพื่อให้การฝึกสามารถทำงานได้ดี. เปรียบเทียบ (ก) การไม่ทำนอร์มอไลซ์ กับ (ข) การทำนอร์มอไลซ์ให้อยู่ในช่วง \([0,1]\) และ (ค) การทำนอร์มอไลซ์ให้อยู่ในช่วง \([-1,1]\) และ (ง) การทำนอร์มอไลซ์ให้ค่าเฉลี่ย และค่าเบี่ยงเบนมาตราฐาน เป็น \(0\) และ \(1\) ตามลำดับ. เปรียบเทียบ อภิปรายผล และสรุป พร้อมเขียนโปรแกรมเพื่อวาดกราฟนำเสนอผลสรุป.
คำใบ้ ดูคำสั่ง np.random.rand. การทดลองกรณีง่ายก่อน จะช่วยให้การเลือกค่าอภิมานพารามิเตอร์สะดวกขึ้น. กรณีง่าย หมายถึง กรณีที่น่าจะช่วยให้การฝึกแบบจำลองทำได้ง่ายกว่า.
หมายเหตุ รายการ [code: normalize1] แสดงโปรแกรมสำหรับการนอร์มอไลซ์อินพุตแบบกำหนดช่วง. ศึกษาโปรแกรม ทดลองใช้ อภิปราย และเขียนโปรแกรมสำหรับการนอร์มอไลซ์อินพุตแบบค่าสถิติ ทดสอบ แล้วนำโปรแกรมนอร์มอไลซ์อินพุตทั้งสองแบบ ไปทำการทดลอง.
def normalize1(X, params=None):
# X: D x N
xmax = np.max(X, axis=1)
xmin = np.min(X, axis=1)
if params is not None:
xmax = params['xmax']
xmin = params['xmin']
else:
params = {'xmax': xmax, 'xmin': xmin}
xmax = xmax.reshape((-1, 1))
xmin = xmin.reshape((-1, 1))
xn = (X - xmin)/(xmax - xmin)
return xn, params3.1.0.1.2 แบบฝึกหัด
ชุดข้อมูลเรือยอชต์ (yacht dataset) จากคลังข้อมูลยูซีไอ ซึ่งดาวน์โหลดที่ http://archive.ics.uci.edu/ml/datasets/Yacht+Hydrodynamics มีภารกิจ คือการประมาณค่าแรงต้านที่เหลือค้าง (residuary resistance) ของเรือยอชต์ขณะแล่น ซึ่งเป็นปัญหาการหาค่าถดถอย. ข้อมูลชุดนี้มี \(308\) ระเบียน นั่นคือ มี \(308\) จุดข้อมูล และแต่ละจุดข้อมูลจะมี \(7\) เขตข้อมูล (\(7\) ลักษณะสำคัญ). ตามมุมมองของฐานข้อมูล (database) จุดข้อมูล จะเรียก ระเบียน (record) และคุณลักษณะสำคัญต่าง ๆในระเบียน จะเรียก เขตข้อมูล (field).
ชุดข้อมูลเรือยอชต์นี้ เขตข้อมูลที่หนึ่ง ตำแหน่งตามแนวยาวเรือของศูนย์กลางการลอยตัว (longitudinal position of the center of buoyancy) เป็นลักษณะที่ช่วยอธิบายการกระจายน้ำหนักของเรือตามแนวยาว ว่าน้ำหนักกระจายอยู่หน้าลำ กลางลำ หรือท้ายลำอย่างไร. เขตข้อมูลที่สอง ค่าสัมประสิทธิปริซึ่ม (prismatic coefficient) เป็นลักษณะที่ช่วยอธิบายรูปทรงของท้องเรือ โดยวัดจากอัตราส่วนของปริมาตรที่อยู่ใต้น้ำของท้องเรือ เปรียบเทียบกับปริมาตรของรูปทรงปริซึ่มที่มีความยาวเท่ากัน และพื้นที่หน้าตัดเท่ากับ พื้นที่หน้าตัดที่กว้างที่สุดของท้องเรือ. เขตข้อมูลที่สาม อัตราส่วนความยาวเรือกับการกระจัด (length-displacement ratio) เป็นลักษณะที่ช่วยบ่งชี้ถึงความหนักของเรือ เมื่อเทียบกับความยาว เรือที่หนักจะมีค่านี้มาก เรือที่เบาจะมีค่านี้น้อย. เขตข้อมูลที่สี่ อัตราส่วนความกว้างเรือกับระดับจมน้ำ (beam-draught ratio) เป็นลักษณะทรงท้องเรือที่วัดจาก อัตราส่วนความกว้างเรือ กับความกว้างของส่วนที่กว้างที่สุดของเรือในแนวระดับน้ำ. เขตข้อมูลที่ห้า อัตราส่วนความยาวกับความกว้างเรือ (length-beam ratio). เขตข้อมูลที่หก ตัวเลขฟรูด (Froude number) เป็นค่าที่บอกความต้านทานของการที่วัตถุเคลื่อนที่ในน้ำ. เขตข้อมูลทั้งหกนี้ บรรยายลักษณะรูปร่าง และการกระจายน้ำหนักของท้องเรือ และเขตข้อมูลเหล่านี้จะใช้เป็นอินพุตของแบบจำลอง.
เขตข้อมูลที่เจ็ด (Residuary resistance per unit weight of displacement) เป็นค่าความต้านทานเหลือค้าง ซึ่งเป็นแรงต้านสำคัญที่เกิดกับเรือ และเกี่ยวพันกับลักษณะต่าง ๆ ของเรือ (ที่บรรยายด้วยหกเขตข้อมูลแรก). การประมาณค่าความต้านทานเหลือค้างได้แม่นยำ จะช่วยในการประเมินสมถนะของเรือได้ดี รวมถึงช่วยเป็นข้อมูลประกอบ สำหรับการออกแบบเรือด้วย เช่น การเลือกรูปทรงและขนาดของท้องเรือ การกำหนดน้ำหนักบรรทุกของเรือ การเลือกขนาดของเครื่องยนต์ที่เหมาะสม. (ดูคำอธิบายเพิ่มเติมจากคลังข้อมูลยูซีไอ และอรทิโกสาและคณะ.)
ข้อมูลมี \(308\) ตัวอย่าง และสามารถอ่านข้อมูลเข้าได้ดังเช่นไฟล์ข้อความทั่วไป ดังแสดงในโปรแกรมตัวอย่างข้างล่าง เมื่อไฟล์ข้อมูลถูกดาวน์โหลดมาในชื่อ yacht_hydrodynamics.data.
with open('yacht_hydrodynamics.data', 'r') as f:
yacht = f.read()ข้อมูลที่นำเข้ามาจะอยู่ในรูปข้อความ เพื่อประสิทธิภาพในการประมวลผล ควรจัดข้อมูลเข้าในรูปนัมไพอาร์เรย์ก่อน ดังแสดงด้วยคำสั่งข้างล่าง
dataxy = []
lines = yacht.split('\n')
i = 0
for line in lines:
i += 1
row = []
j = 0
flag = False
for d in line.split(' '):
j += 1
try:
c = float(d)
row.append(c)
except:
flag = True
# end for d
if flag: print(i, ',', j, '; d:', row)
if len(row) > 0: dataxy.append(row)
# end for line
Dataxy = np.array(dataxy)เมื่อ Dataxy คือข้อมูลในรูปแบบ np.array ขนาด \(308 \times 7\). รูป 7 แสดงความสัมพันธ์ระหว่างเขตข้อมูลที่หนึ่งถึงหก (ทีละเขตข้อมูล) กับเขตข้อมูลที่เจ็ด (ที่เป็นตัวแปรตาม) หลังจากแบ่งข้อมูลแล้ว. ในตัวอย่างนี้ ข้อมูล \(185\) จุดข้อมูล (ประมาณ \(60\%\)) ถูกแบ่งเป็นชุดฝึก (trainx และ trainy) และที่เหลือเป็นชุดทดสอบ (testx และ testy).
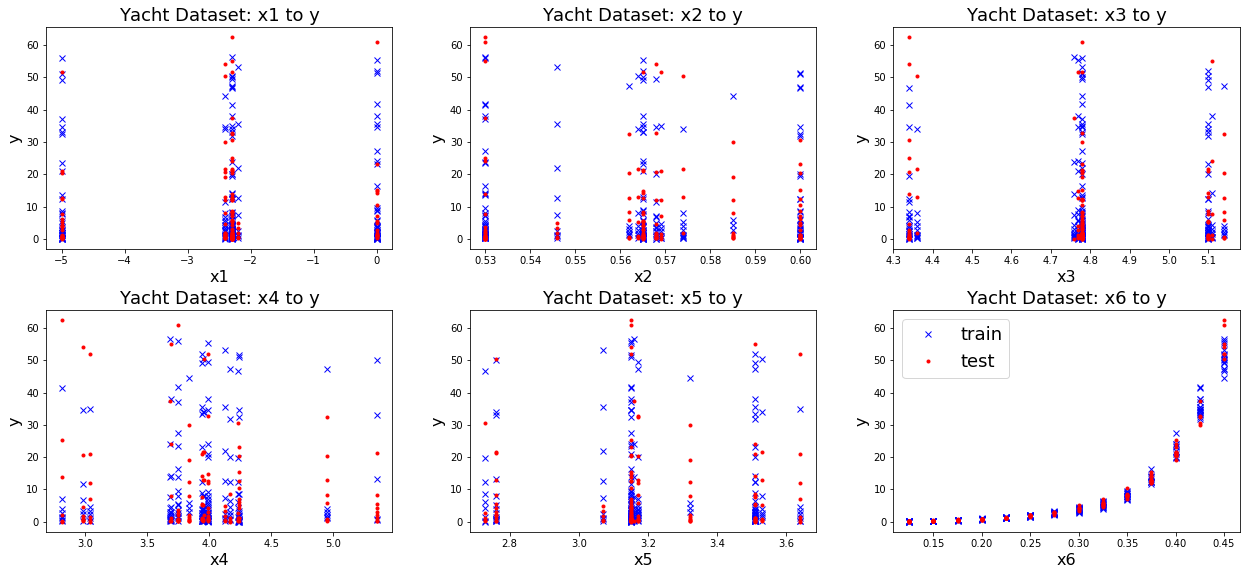
จากรูป 7 สังเกตว่า อินพุตมิติต่าง ๆ มีขนาดแตกต่างกันพอสมควร เช่น \(x_1\) (ภาพซ้ายบน) มีขนาดตั้งแต่ \(-5\) ถึ \(0\) ในขณะที่ \(x_6\) (ภาพขวาล่าง) มีขนาดไม่เกิน \(0.5\). เพื่อช่วยให้การฝึกแบบจำลองทำได้ง่ายขึ้น สถานการณ์เช่นนี้ ควรนอร์มอไลซ์อินพุต (หัวข้อ [sec: ann applications]).
จงสร้างแบบจำลองโครงข่ายประสาทเทียม เพื่อประมาณค่าความต้านทานเหลือค้าง จากคุณลักษณะทั้งหกของเรือ โดยใช้ชุดข้อมูลเรือยอชต์ ในการฝึก และการทดสอบ โดยแบ่งข้อมูลให้เรียบร้อย ทำนอร์มอไลซ์อินพุต อภิปรายว่า กรณีนี้การนอร์มอไลซ์ชนิดใด (ระหว่างนอร์มอไลซ์เข้าสู่ช่วงที่จำกัด กับนอร์มอไลซ์เข้าสู่ค่าสถิติที่กำหนด) เหมาะสมมากกว่ากัน พร้อมเหตุผลประกอบ. หลังจากฝึกและทดสอบเสร็จ นำเสนอผลให้ชัดเจน. รูป 8 แสดงตัวอย่างการนำเสนอผล.
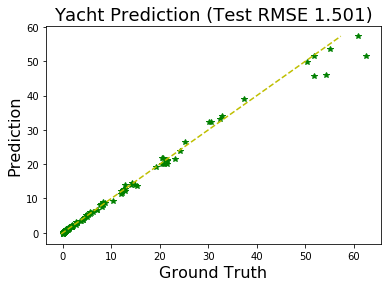
การฝึกด้วยโปรแกรม ดังรายการ [code: train_mlp] ซึ่งใช้ข้อมูลฝึกทั้งหมดในการปรับค่าพารามิเตอร์ทีเดียว เป็นการฝึกแบบหมู่ (หัวข้อ [sec: online and batch training]). เมื่อสามารถทำแบบจำลองประมาณค่าความต้านทานเหลือค้างได้ดีพอสมควรแล้ว ศึกษาความแปรปรวนของผล ด้วยการทำซ้ำ และเปรียบเทียบผลกับการฝึกแบบออนไลน์.
รายการ [code: train_online] แสดงตัวอย่างโปรแกรมฝึกโครงข่ายประสาทเทียม โดยใช้วิธีการฝึกแบบออนไลน์ (เปรียบเทียบกับรายการ [code: train_mlp]). รูป 10 แสดงผลความแม่นยำ ที่ได้จากการฝึกแบบหมู่ เปรียบเทียบกับแบบออนไลน์ จากการทดลองซ้ำ \(40\) ครั้ง.
def train_online(net_params, trainX, trainY, loss, lr, epochs):
num_layers = net_params['layers']
last_layer = num_layers-1
out_act = 'act%d'%last_layer
_, N = trainX.shape
A = {}
delta = {}
dEw = {}
dEb = {}
train_losses = []
step_size = lr/N
for nt in range(epochs):
for n in range(N): # ONLINE! through each datapoint
Z = {0: trainX[:,[n]]} # ONLINE!
# (1) Forward pass
for i in range(1, num_layers):
b = net_params['bias%d'%i]
w = net_params['weight%d'%i]
act_f = net_params['act%d'%i]
A[i] = np.dot(w, Z[i-1]) + b
Z[i] = act_f(A[i])
# end forward pass
Yp = Z[i]
# (2) Calculate output dE/da
delta[last_layer] = Yp - trainY[:,[n]] # ONLINE!
# (3) Backpropagate
for i in range(last_layer, 1, -1):
b = net_params['bias%d'%i]
w = net_params['weight%d'%i]
act_f = net_params['act%d'%(i-1)]
sumdw = np.dot(w.transpose(), delta[i])
assert act_f == sigmoid
delta[i - 1] = dsigmoid(Z[i - 1]) * sumdw
# (4) Calculate gradient dE/dw and dE/db
dEw[i] = np.dot(delta[i], Z[i-1].transpose())
dEb[i] = delta[i] # ONLINE!
# end backpropagate
# Calculate gradient
dEw[1] = np.dot(delta[1], Z[0].transpose())
dEb[1] = delta[1] # ONLINE!
# Update parameters
for i in range(1, num_layers):
b = net_params['bias%d'%i]
w = net_params['weight%d'%i]
b -= step_size * dEb[i]
w -= step_size * dEw[i]
# end update parameters
# end ONLINE through each datapoint
# Calculate loss at each epoch
Yp = mlp(net_params, trainX)
lossn = np.sum(loss(Yp, trainY), axis=0)
train_losses.append(np.mean(lossn))
# end epoch nt
return net_params, train_losses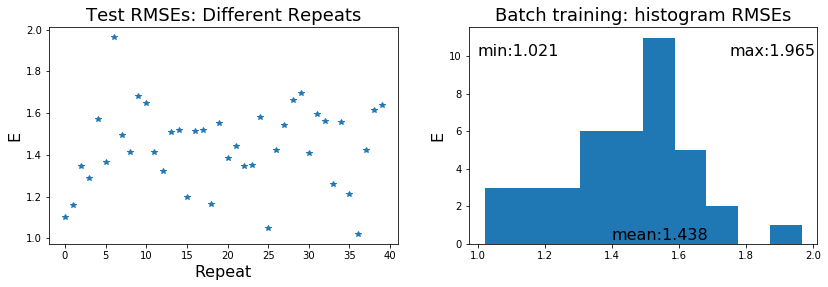
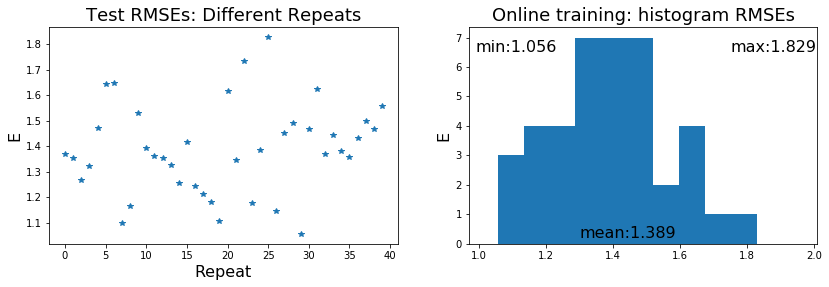
ในกรณีนี้ ดังผลที่แสดงในรูป 10 ความแม่นยำที่ได้ ไม่ได้แตกต่างกันเท่าไร แต่เวลาในการฝึกต่างกันมาก เช่นในการทดลองตัวอย่าง การฝึกแบบออนไลน์ใช้เวลาเป็น \(36\) เท่าของเวลาฝึกแบบหมู่.
3.1.0.1.3 แบบฝึกหัด
ข้อมูลชุดภาพเอ็กซเรย์เต้านมของมวลเนื้อ (Mammographic Mass dataset) จากคลังข้อมูลยูซีไอที่ http://archive.ics.uci.edu/ml/datasets/Mammographic+Mass เอลเตอร์และคณะ ใช้ศึกษาการทำนายผลการตรวจภาพเอ็กซเรย์เต้านม ของร่องรอยมวลเนื้อ (mammographic mass lesion) ว่าเป็นเนื้อดี (benign) หรือเนื้อร้าย (malignant) จากค่าลักษณะสำคัญต่าง ๆ ของของภาพ ประกอบกับอายุของผู้ป่วย. วิธีตรวจภาพเอ็กซเรย์เต้านม (Mammography) เป็นวิธีที่มีประสิทธิผลมากในการตรวจมะเร็งทรวงอก . ข้อมูลชุดนี้ประกอบด้วย ค่าการประเมินไบแรตส์ (BI-RADS assessment เป็นค่าเชิงเลขลำดับ ordinal values), อายุของผู้ป่วย (เลขจำนวนเต็ม), รูปทรงของมวลเนื้อ (mass shape ซึ่งถูกแทนด้วย 1 สำหรับทรงกลม round, 2 สำหรับทรงรี oval, 3 สำหรับทรงกลีบย่อย lobular, 4 สำหรับทรงที่ผิดแปลก irregular), ลักษณะขอบของมวลเนื้อ (mass margin ซึ่งถูกแทนด้วย 1 สำหรับเขตรอบชัดเจน circumscribed, 2 สำหรับขอบเขตเป็นกลีบย่อย ๆ microlobulated, 3 สำหรับขอบเขตคลุมเครือ obscured, 4 สำหรับขอบเขตยากจะระบุ ill-defined, 5 สำหรับขอบเขตเป็นลักษณะหนามหรือปุ่ม spiculated), ความหนาแน่นของมวลเนื้อ (mass density ซึ่งถูกแทนด้วย 1 สำหรับความหนาแน่นสูง high, 2 สำหรับความหนาแน่นกลาง ๆ iso, 3 สำหรับความหนาแน่นต่ำ low, 4 สำหรับมวลเนื้อมีไขมันอยู่ fat-containing) และความร้ายแรง (severity ซึ่งมีสองค่า 0 สำหรับเนื้อดี หรือ 1 สำหรับเนื้อร้าย). ค่าความร้ายแรง คือค่าเป้าหมาย ที่ต้องการทำนาย. การสามารถทำนายค่าความร้ายแรงได้อย่างแม่นยำจะช่วยให้แพทย์และผู้ป่วยสามารถตัดสินใจได้ดีขึ้นว่า ควรจะทำการตัดเนื้อจากบริเวณที่สงสัยออกตรวจเพื่อยืนยันผลหรือไม่.
ข้อมูลชุดนี้มี \(961\) ระเบียน เฉลยหรือผลการตรวจจริง ระบุ \(516\) ระเบียนที่ผลเป็นเนื้อดี (ค่าความร้ายแรง เป็นศูนย์) และ \(445\) ระเบียนที่ผลเป็นเนื้อร้าย (ค่าความร้ายแรง เป็นหนึ่ง). ข้อมูลชุดนี้มีค่าบางค่าของเขตข้อมูลที่ไม่ครบ (missing attribute values) ได้แก่ ค่าการประเมินไบแรตส์ขาดไป \(2\) ค่า, อายุขาดไป \(5\) ค่า, รูปทรงของมวลเนื้อขาดไป \(31\) ค่า, ลักษณะขอบของมวลเนื้อขาดไป \(48\) ค่า และความหนาแน่นของมวลเนื้อขาดไป \(76\) ค่า. ส่วนความร้ายแรงมีค่าครบทุกระเบียน.
จงทำแบบจำลองโครงข่ายประสาทเทียมเพื่อทำนายค่าความร้ายแรง จากลักษณะสำคัญ ด้วยข้อมูลชุดภาพเอ็กซเรย์เต้านม เลือกแบบจำลอง ฝึก ทดสอบ วัดผล รายงานผลที่ได้ อภิปราย และสรุป. ภาระกิจนี้ เป็นการจำแนกค่าทวิภาค ที่เอาต์พุต คือความร้ายแรง ซึ่งมีค่าเป็นหนึ่งหรือศูนย์. การจัดการกับข้อมูลขาดหาย สามารถดำเนินการได้หลายแนวทาง. แนวทางหนึ่ง ซึ่งเป็นแนวทางที่ง่ายที่สุด คือตัดระเบียนที่มีข้อมูลขาดหายทิ้งทั้งระเบียน.
คำสั่งข้างล่าง แสดงตัวอย่างการอ่านไฟล์ข้อมูล mammographic_masses.data และเตรียมข้อมูล
with open('mammographic_masses.data', 'r') as f:
mammo_text = f.read()
mammo1 = []
for line in mammo_text.split('\n'):
row = []
complete = True
for field in line.split(','):
try:
val = int(field)
except:
complete = False
val = None
row.append(val)
if complete:
mammo1.append(row)
else:
mammo_miss.append(row)
# end for line
mammo1 = np.array(mammo1)ซึ่งผลลัพธ์จะคือ mammo1 ซึ่งเป็นนัมไพอาร์เรย์ขนาด \(830 \times 6\) ซึ่งทุกแถว (ทุกระเบียนข้อมูล) ครบถ้วนสมบูรณ์ ไม่มีข้อมูลขาดหาย. ในขณะที่ mammo_miss เป็นลิสต์ของระเบียนข้อมูลที่เหลือ และทุกระเบียนใน mammo_miss มีข้อมูลที่ขาดหายไป (ดูย่อหน้า การจัดการกับข้อมูลขาดหาย).
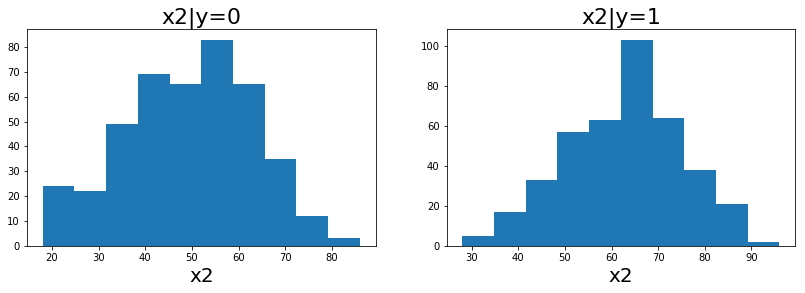
ข้อมูลของ mammo1 แสดงในรูป 11, 12 และ 15. สังเกตว่า ข้อมูลชุดภาพเอ็กซเรย์เต้านมนี้ อินพุตมิติแรก (รูป 11 และคำอธิบายข้อมูล ที่สามารถดาวน์โหลดได้พร้อมไฟล์ข้อมูล) เป็นค่าเชิงเลขลำดับ ซึ่งสามารถคิดเสมือนว่าเป็นค่าตัวเลขได้. อินพุตมิติที่สอง เป็นจำนวนเต็มแสดงอายุ ซึ่งเป็นตัวเลขจริง ๆ. แต่อินพุตมิติที่สามถึงห้า (รูป 15) เป็นค่าแทนชื่อ (nominal values) ซึ่งไม่ได้มีความหมายเป็นปริมาณตามขนาดใหญ่เล็กของตัวเลขจริง ๆ ตัวเลขทำหน้าที่ แค่เป็นดัชนีเพื่ออ้างถึงชื่อเท่านั้น.
รูป 16 แสดงผลลัพธ์ของการทำนาย ด้วยแผนภูมิกล่อง จากตัวอย่างผลการทำนายของ แบบจำลองที่ทำโดยไม่สนใจความหมายของอินพุต (กล่องซ้าย ระบุด้วยชื่อ Naive) และแบบจำลองที่ทำการเข้ารหัสอินพุตให้เหมาะสมกับความหมาย (กล่องขวา ระบุด้วยชื่อ Coding). แบบจำลองที่ทำโดยไม่สนใจความหมายของอินพุต นั่นคือ ใช้ค่าตัวเลขของข้อมูลใส่เป็นอินพุตให้กับแบบจำลองโดยตรง เช่น ในตัวอย่างข้างล่าง ที่เพียงทำนอร์มอไลซ์อินพุต
trainx = mammo1[train_ids,:5].transpose() # 5 x N
trainy = mammo1[train_ids,5].reshape((1,-1)) # 1 x N
testx = mammo1[test_ids,:5].transpose() # 5 x N
testy = mammo1[test_ids,5].reshape((1,-1)) # 1 x N
trainxn, normpars = normalize1(trainx)
# Configure binary classification net
net = w_initn([5, 10, 1])
net['act1'] = sigmoid
net['act2'] = sigmoid
# Train net
trained_net, train_losses = train_mlp(net, trainxn, trainy,
binaries_cross_entropy, lr=0.1, epochs=5000)เมื่อ train_ids และ test_ids เป็นดัชนีที่สุ่มเลือก เพื่อใช้เป็นข้อมูลฝึก และข้อมูลทดสอบ ตามลำดับ. ตัวอย่างผลที่แสดงในแบบฝึกหัดนี้ ได้จากการใช้ข้อมูลจำนวน \(300\) จุดข้อมูลเป็นข้อมูลทดสอบ และใช้ที่ข้อมูลที่เหลือเป็นข้อมูลฝึก (ดูตัวอย่างวิธีแบ่งข้อมูล จากแบบฝึกหัด 1.1.0.0.6). โปรแกรม normalize1, w_initn, sigmoid และ train_mlp ได้อภิปรายไปแล้ว ดังรายการ [code: normalize1], [code: w_initn], [code: sigmoid] และ [code: train_mlp] ตามลำดับ. ส่วนโปรแกรม binaries_cross_entropy เป็นฟังก์ชันสูญเสียครอสเอนโทรปีแบบทวิภาค ที่นิยมใช้กับงานจำแนกค่าทวิภาค แสดงในรายการ [code: binaries_cross_entropy].
def binaries_cross_entropy(yhat, y):
assert yhat.shape == y.shape
loss = yhat.copy()
zero_ids = np.where(y == 0)
loss[zero_ids] = 1 - loss[zero_ids]
loss = -np.log(loss)
return loss # output: K x Nหลังจากการฝึกสมบูรณ์แล้ว แบบจำลองถูกทดสอบดังคำสั่งตัวอย่างข้างล่างนี้
testxn, _ = normalize1(testx, normpars)
Yp = mlp(trained_net, testxn)
Yc = cutoff(Yp)
accuracy = np.mean(Yc == testy)เมื่อ Yp เป็นค่าที่ทำนายจากแบบจำลอง ซึ่งมีค่าอยู่ในช่วง \([0,1]\) และเพื่อบังคับให้ผลตัดสินใจเป็น \(0\) หรือ \(1\) จึงใช้โปรแกรม cutoff ช่วย. ผลประเมินความแม่นยำของแบบจำลองจำแนกทวิภาค อาจวัดด้วยค่าความแม่นยำ accuracy ที่มีค่าระหว่างศูนย์ถึงหนึ่ง และค่าใกล่หนึ่งหมายถึงความแม่นยำสูง. โปรแกรม cutoff เขียนด้วยคำสั่งดังนี้
def cutoff(a, tau=0.5):
return (a > tau)*1ผลลัพธ์ที่แสดงในรูป 16 ได้มาจากการทดลองซ้ำ \(40\) ครั้ง. แบบจำลอง naive สร้างโดยไม่สนใจความหมายของข้อมูล ดังได้อภิปรายไป. ส่วนแบบจำลอง coding สร้างโดยแปลงอินพุตเป็นรหัสตามความหมายของลักษณะสำคัญ แต่ละอย่าง โดยเฉพาะลักษณะสำคัญที่สามถึงห้า ซึ่งเป็นค่าแทนชื่อ ได้แก่ รูปทรงของมวลเนื้อ ลักษณะขอบของมวลเนื้อ และความหนาแน่นของมวลเนื้อ. แบบจำลอง coding เข้ารหัสลักษณะทั้งสาม ด้วยรหัสหนึ่งร้อน โดยคำสั่ง trainxc, cparams = mammo_coding(trainx). นอกจากลักษณะสำคัญทั้งสาม ลักษณะสำคัญที่หนึ่งถูกเข้ารหัสเป็นระดับค่า และลักษณะสำคัญที่สอง ซึ่งเป็นอายุ ถูกนอร์มอไลซ์ด้วยค่าสถิติ. โปรแกรม mammo_coding เขียนด้วยคำสั่งดังนี้
def mammo_coding(xin, cpars=None):
d0 = xin[[0],:].copy()
d0[d0 > 5] = 5 # make it {0,...,5}
d1 = xin[[1],:].copy()
d2 = xin[[2],:].copy()
d3 = xin[[3],:].copy()
d4 = xin[[4],:].copy()
code0 = coding(d0, level_cbook(6)) # ordinal
code1, cpars = normalize2(d1, cpars) # age normalized with stats
z4code = np.vstack( (np.zeros((1,4)), onehot_cbook(4)) )
z5code = np.vstack( (np.zeros((1,5)), onehot_cbook(5)) )
code2 = coding(d2, z4code) # nominal
code3 = coding(d3, z5code) # nominal
code4 = coding(d4, z4code) # nominal
return np.vstack((code0, code1, code2, code3, code4)), cparsเมื่อ normalize2 เป็นโปรแกรมนอร์มอไลซ์อินพุต (ดูแบบฝึกหัด 1.1.0.1.1) และ coding, onehot_cbook และ level_cbook เขียนดังนี้
def coding(xin, code_book):
'''
xin: 1 x N
code_book: np.array in K x C, K: key of x, C: code
'''
return code_book[xin][0].transpose()
def onehot_cbook(K):
return np.diag(np.ones((K,)))
def level_cbook(K):
return np.tril(np.ones((K,K)))การเข้ารหัสอินพุตเช่นนี้ ทำให้อินพุตที่เข้าแบบจำลองกลายเป็น \(20\) มิติ แต่ช่วยให้ผลการทำงานดีขึ้นอย่างชัดเจน ดังตัวอย่างผลลัพธ์ที่แสดงในรูป 16. รูป 16 รายงานผลด้วยค่าความแม่นยำ ในช่วง \(0\) ถึง \(1\). บางครั้ง ค่าความแม่นยำนิยมรายงานเป็นเปอร์เซ็นต์ เช่น ค่าความแม่นยำเฉลี่ยเป็น \(80.9\%\) และ \(82.3\%\) สำหรับแบบจำลอง naive และแบบจำลอง coding.
นอกจากการรายงานผลด้วยค่าความแม่นยำแล้ว เมทริกซ์ความสับสน (confusion matrix) เป็นการแจกแจงผลการทำงานออกเป็นสี่ชนิด คือ จำนวนบวกจริง (true positive คำย่อ TP), จำนวนบวกเท็จ (false positive คำย่อ FP), จำนวนลบจริง (true negative คำย่อ TN) และจำนวนลบเท็จ (false negative คำย่อ FN). จำนวนบวกจริง คือจำนวนจุดข้อมูลทดสอบที่ถูกทายเป็น \(1\) และเฉลยเป็น \(1\). จำนวนบวกเท็จ คือจำนวนจุดข้อมูลทดสอบที่ถูกทายเป็น \(1\) แต่เฉลยเป็น \(0\). จำนวนลบจริง คือจำนวนจุดข้อมูลทดสอบที่ถูกทายเป็น \(0\) และเฉลยเป็น \(0\). จำนวนลบเท็จ คือจำนวนจุดข้อมูลทดสอบที่ถูกทายเป็น \(0\) แต่เฉลยเป็น \(1\).
ตัวอย่างเมทริกซ์ความสับสน แสดงข้างล่าง
| ผลจริง | ||||
| 1 | 0 | |||
| True Positive | False Positive | |||
| ผลทำนาย | 1 | 130 | 26 | Precision = 0.833 |
| False Negative | True Negative | |||
| 0 | 25 | 119 | ||
| Recall = 0.839 | ||||
นอกจากเมทริกซ์ความสับสนแล้ว ตัวอย่างยังรายงานค่าความเที่ยงตรง (precision) และค่าการระลึกกลับ (recall) ที่ด้านข้าง และด้านล่างของเมทริกซ์ความสับสนด้วย.
ค่าความเที่ยงตรงและค่าการระลึกกลับ ออกแบบ โดยคำนึงถึง ความสมดุลของการแจกแจงของกลุ่มข้อมูล. ข้อมูลชุดนี้มีการแจกแจงข้อมูลพอ ๆ กัน. ข้อมูลกลุ่ม 1 (ผลเป็นเนื้อร้าย) และข้อมูลกลุ่ม 0 (ผลเป็นเนื้อดี) มีจำนวนระเบียนใกล้เคียงกัน คือ \(445\) ระเบียนและ \(516\) ระเบียน ตามลำดับ. ลักษณะการแจกแจงเช่นนี้ ทำให้ค่าความแม่นยำ สามารถสะท้อนคุณภาพการทำนายจริงของแบบจำลองได้ดี. แต่หากการแจกแจงไม่สมดุลอย่างมาก เช่น สมมติอัตราส่วนคนเป็นมะเร็งตับอ่อนต่อประชากรมีค่าน้อยกว่า \(1\%\) เพียงแต่แบบจำลองทำนายผลเป็น \(0\) คือไม่เป็นมะเร็ง สำหรับทุก ๆ ตัวอย่างที่เข้ามาทดสอบ แบบจำลองนั้นก็มีโอกาสถูกถึง \(99\%\) (ความแม่นยำ เป็น \(0.99\)) นั่นคือ เท่ากับทายว่าไม่มีใครเป็นมะเร็งตับอ่อนเลย ซึ่งแม้จะมีโอกาสทายถูกสูงมาก ๆ แต่มันไม่ได้มีประโยชน์ต่อการช่วยระบุกลุ่มเสี่ยงเลย.
ดังนั้นแทนที่จะใช้แค่ค่าความแม่นยำ ค่าความเที่ยงตรง (สมการ \(\eqref{eq: precision}\)) และค่าการระลึกกลับ (สมการ \(\eqref{eq: recall}\)) จะช่วยสะท้อนคุณภาพการทำนายได้ดีกว่า โดยเฉพาะสำหรับข้อมูลที่มีการแจกแจงข้อมูลไม่สมดุล. การตรวจสอบค่าความเที่ยงตรง และค่าการระลึกกลับ จะช่วยบอกได้ว่าแบบจำลองทำนายได้ดีอย่างสมดุลกับผลทำนาย. สำหรับงานจำแนกค่าทวิภาค ค่าความเที่ยงตรง \(P\) สามารถคำนวณได้จาก \[\begin{eqnarray} P &=& \frac{TP}{TP + FP} \label{eq: precision} \end{eqnarray}\] และค่าการระลึกกลับ \(R\) สามารถคำนวณได้จาก \[\begin{eqnarray} R &=& \frac{TP}{TP + FN} \label{eq: recall} \end{eqnarray}\]
หมายเหตุ เมื่อใช้ค่าความเที่ยงตรงและค่าการระลึกกลับในการวัดผล กับข้อมูลที่มีการแจกแจงไม่สมดุล จะกำหนดให้กลุ่ม 1 (กลุ่มบวก) เป็นกลุ่มที่มีสัดส่วนน้อย (เช่น กลุ่มของมะเร็งตับอ่อน) และกลุ่ม 0 (กลุ่มลบ) เป็นกลุ่มใหญ่ (เช่น กลุ่มที่ไม่ได้เป็น).
ค่าความเที่ยงตรงและค่าการระลึกกลับ ช่วยสะท้อนความสามารถของแบบจำลองได้ดีขึ้น โดยเฉพาะในกรณีที่ข้อมูลมีการแจกแจงระหว่างกลุ่มไม่สมดุล. แต่การรายงานผล ด้วยตัวเลขสองตัวนั้น อาจทำให้ลำบากในการเปรียบเทียบผล เช่น ผลของแบบจำลองหนึ่ง อาจจะได้ค่าความเที่ยงตรงสูง แต่ค่าการระลึกกลับต่ำ แต่อีกแบบจำลองหนึ่ง มีค่าความเที่ยงตรงต่ำ แต่ค่าการระลึกกลับสูง. เพื่อความสะดวก ค่าคะแนนเอฟ (F Score หรือ บางครั้งเรียก F1 Score) ซึ่งเป็นค่าเฉลี่ยเชิงเรขาคณิต มักใช้ในการสรุป ค่าความเที่ยงตรง และค่าการระลึกกลับ ให้เป็นตัวเลขตัวเดียว. ค่าคะแนนเอฟ สัญกรณ์ \(F\) สามารถคำนวณได้จาก \[\begin{eqnarray} F = 2 \cdot \frac{P \cdot R}{P + R} \label{eq: F score}. \end{eqnarray}\]
จากเมทริกซ์ความสับสนในตัวอย่าง ค่าคะแนนเอฟ จะเท่ากับ \(0.836\).
สุดท้าย ย้อนกลับมาทบทวนเรื่องผลลัพธ์สุดท้าย จากหัวข้อ [sec: prob cond prob examples] ตัวอย่าง ปัญหาการตรวจเต้านมด้วยภาพเอ็กซเรย์. ตัวอย่างนั้น อภิปรายการคำนวณหา โอกาสที่จะเป็นมะเร็ง เมื่อผลการตรวจระบุว่าเป็น. นั่นคือ หา \(\mathrm{Pr}(C = 1|M = 1)\) เมื่อ \(M = 1\) หมายถึงผลการตรวจระบุว่าเป็นมะเร็ง และ \(C = 1\) หมายถึงการเป็นมะเร็งจริง ๆ.
ข้อมูลประกอบ คือ \(17\%\) ของผู้หญิงอายุเกิน 40 ปีเป็นมะเร็งเต้านม นั่นคือ \(\mathrm{Pr}(C = 1) = 0.17\). ค่า \(\mathrm{Pr}(M = 1|C = 1)\) สามารถประมาณได้จากค่าในเมทริกซ์ความสับสน \(\mathrm{Pr}(M = 1|C = 1) \approx R\) เมื่อ \(R\) คือค่าระลึกกลับ ซึ่งในตัวอย่างนี้เป็น \(0.839\) และค่า \(\mathrm{Pr}(M = 1|C = 0)\) ประเมินได้จาก \(\mathrm{Pr}(M = 1|C = 0) \approx \frac{FP}{FP + TN}\) ซึ่งในตัวอย่างนี้เป็น \(\frac{26}{26 + 119} = 0.179\).
เมื่อรวมหลักฐานทุกอย่างเข้าด้วยกัน โดยใช้กฎของเบยส์ จะได้ว่า \[\begin{eqnarray} \mathrm{Pr}(C = 1|M = 1) &=& \frac{\mathrm{Pr}(M = 1|C = 1) \mathrm{Pr}(C = 1)}{\mathrm{Pr}(M = 1|C = 0) \mathrm{Pr}(C = 0) + \mathrm{Pr}(M = 1|C = 1) \mathrm{Pr}(C = 1)} \nonumber \\ &=& \frac{0.839 \cdot 0.17}{0.179 \cdot 0.83 + 0.839 \cdot 0.17} = 0.4898 \nonumber . \end{eqnarray}\] ดังนั้น ผลตรวจภาพเอ็กซเรย์เต้านม จึงเป็นเสมือนแค่การตรวจเบื้องต้น เพื่อประกอบการตัดสินใจ ตัดชิ้นเนื้อไปตรวจ (biopsy).
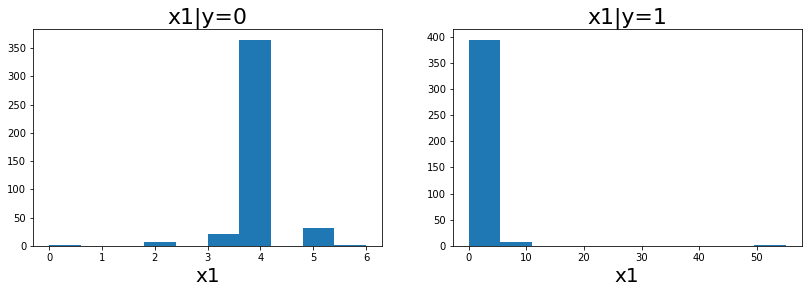
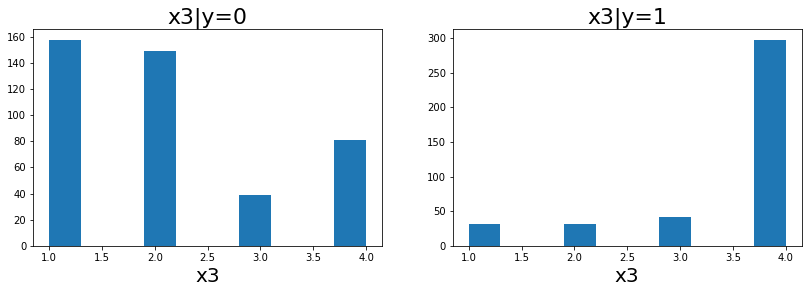
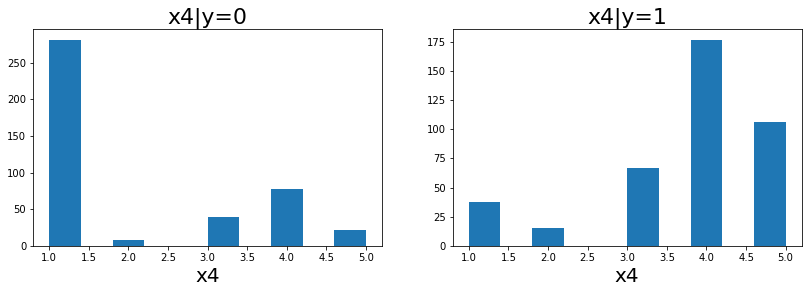


3.1.0.2 การจัดการกับข้อมูลขาดหาย.
แบบฝึกหัด 1.1.0.1.3 แนะนำวิธีตัดระเบียนที่มีข้อมูลขาดหายทิ้งไป ซึ่งเป็นหนึ่งในแนวทางที่นิยม และดำเนินการได้ง่าย. นอกจากแนวทางตัดระเบียนทิ้ง ยังมีแนวทางอื่น ๆ อีก เช่น วิธีการแทนค่าข้อมูลที่ขาดหายไป ด้วยค่าเฉลี่ย สำหรับมิติหรือเขตข้อมูลที่เป็นค่าต่อเนื่อง (continuous-value field) หรือแทนด้วยค่าที่พบบ่อยที่สุด ในกรณีที่เขตข้อมูลเป็นค่าแทนชื่อ ฉลาก หรือหมวดหมู่ (categorical field). อีกวิธีที่นิยม คือ วิธีการแทนค่าที่หายไป ด้วยค่าทุกค่าที่เป็นไปได้. วิธีนี้ ระเบียนที่ข้อมูลขาดหายไป จะถูกแทนด้วยระเบียนใหม่หลาย ๆ ระเบียน โดยค่าข้อมูลต่าง ๆ ของระเบียนใหม่ จะเหมือนระเบียนเดิม ยกเว้นข้อมูลที่หายไป จะถูกแทนด้วยค่าหนึ่ง ในกลุ่มค่าที่เป็นไปได้. จำนวนระเบียนใหม่นี้จะเท่ากับจำนวนค่าที่เป็นไปได้ของเขตข้อมูลที่ข้อมูลขาดหายไป. ดูกรึซีมาลาบุสเสและฮูเพิ่มเติม สำหรับวิธีต่าง ๆ ในการจัดการข้อมูลที่ขาดหายไป. นอกจากนั้น การเรียนรู้แบบกึ่งมีผู้ช่วยสอน ยังเสนอแนวทางที่น่าสนใจ ในจัดการกับข้อมูลขาดหายไป โดยเฉพาะกับฉลากที่ขาดหายไป.
วิธีแทนค่าขาดหายด้วยทุกค่าที่เป็นไปได้ การดำเนินการจะยุ่งยากกว่าวิธีอื่น ๆ คำสั่งข้างล่างแสดงตัวอย่างวิธีทำ
mammo3 = []
for row in mammo_miss[:-1]:
mammo3.extend(fix_row(row, field_vals))เมื่อ mammo_miss เป็นลิสต์ของระเบียนที่มีข้อมูลขาดหาย. โปรแกรม fix_row แสดงในรายการ [code: fix_row] และการทดลองตัวอย่าง กำหนด field_vals ด้วย
field_vals = {0: [0, 2, 3, 4, 5], 1: list(range(18, 97, 6)),
2: [1, 2, 3, 4],
3: [1, 2, 3, 4, 5], 4: [1, 2, 3, 4]}สังเกต การทดลองตัวอย่างเลือกแทนค่าอายุเป็นช่วง ๆ ช่วงละหกปี แทนการแทนทุกค่าที่เป็นไปได้ ซึ่งหากทำทุกค่า ในกรณีนี้ อาจเพิ่มจำนวนระเบียนขึ้นมหาศาลโดยไม่จำเป็น.
def fix_row(row, fix_vals):
rows = [row]
i = 0
while i < len(rows):
flag_next = True
for j, c in enumerate(rows[i]):
if c is None:
for v in fix_vals[j]:
newrow = rows[i].copy()
newrow[j] = v
rows.append(newrow)
del rows[i]
flag_next = False
break
# end for j, c
if flag_next:
i += 1
# end while i
good_rows = rows
return good_rows| ค่าความแม่นยำ | ||
| วิธี | ค่าเฉลี่ย | ค่าเบี่ยงเบนมาตราฐาน |
| ตัดระเบียนไม่สมบูรณ์ออก | \(0.8314\) | \(0.0073\) |
| แทนด้วยค่าเฉลี่ย หรือค่าพบบ่อยที่สุด | \(0.8308\) | \(0.0063\) |
| แทนด้วยทุกค่าที่เป็นไปได้ | \(0.8093\) | \(0.0070\) |
| แทนด้วยรหัสศูนย์ | \(0.8203\) | \(0.0061\) |
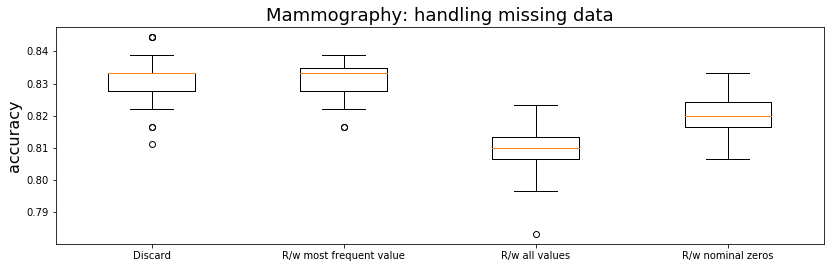
รูป 17 และตาราง 2 แสดงตัวอย่างผลเปรียบเทียบ วิธีจัดการข้อมูลขาดหายแบบต่าง ๆ. นอกจากวิธีทั่วไป ดังอภิปรายข้างต้น ในรูป ยังเสนอผลจากวิธีแทนข้อมูลค่าแทนชื่อที่ขาดหาย ด้วยรหัสศูนย์. เนื่องจากข้อมูลภาพเอ็กซเรย์เต้านม มีเขตข้อมูลหลายเขต ที่เป็นชนิดค่าแทนชื่อ ซึ่งในตัวอย่างของแบบฝึกหัด 1.1.0.1.3 ใช้การเข้ารหัสหนึ่งร้อน (ดูโปรแกรม coding และ onehot_cbook). รหัสหนึ่งร้อน จะใช้ค่าทวิภาพหลายค่า แทนชื่อ โดยมีแค่หนึ่งค่าที่ตำแหน่งสำหรับชื่อนั้น ๆ ที่จะมีค่าเป็นหนึ่ง เพื่อระบุชื่อฉลากนั้น และค่าอื่น ๆ ในรหัสจะเป็นศูนย์ เช่น ฉลากหนึ่ง แทนด้วย \([1, 0, 0, 0]^T\) และฉลากสอง แทนด้วย \([0, 1, 0, 0]^T\) สำหรับกรณีที่มีสี่ฉลาก. ข้อมูลที่ขาดหาย อาจสามารถแทนเป็นรหัสศูนย์ โดยไม่มีหนึ่งที่ตำแหน่งใดในรหัสเลย เช่น \([0, 0, 0, 0]^T\). นี่คือ แนวคิดของวิธีแทนข้อมูลชนิดค่าแทนชื่อที่ขาดหายด้วยรหัสศูนย์ (ระบุด้วย R/w nominal zeros ในภาพ).
3.1.0.2.1 แบบฝึกหัด
ข้อมูลเอมนิสต์ เป็นชุดข้อมูลขนาดใหญ่ของภาพตัวเลขลายมือเขียน พร้อมเฉลย. ชุดข้อมูลประกอบด้วย \(60000\) ตัวอย่าง สำหรับข้อมูลฝึก และ \(10000\) ตัวอย่าง สำหรับข้อมูลทดสอบ. แต่ละตัวอย่าง ตัวเลขในภาพถูกปรับขนาด และปรับจุดศูนย์กลาง และอยู่ในภาพสเกลเทา (gray scale) ขนาด \(28 \times 28\) พิกเซล. คำอธิบาย และข้อมูลเอมนิสต์ สามารถหาได้ที่ http://yann.lecun.com/exdb/mnist/
จงทำแบบจำลองโครงข่ายประสาทเทียม เพื่อรู้จำภาพตัวเลขลายมือเขียน. นั่นคือ สร้างแบบจำลองที่ทายฉลากตัวเลข จากภาพตัวเลขลายมือเขียน เลือกแบบจำลอง ฝึก ทดสอบ วัดผล รายงานผล อภิปราย และสรุป.
ข้อมูลเอมนิสต์อยู่ในไฟล์ชนิดไบนารี (binary file) และเก็บด้วยรูปแบบเอนเดียนใหญ่ (big endian). ไฟล์ฉลาก เช่น train-labels.idx1-ubyte มีส่วนหัว \(8\) ไบต์ ซึ่งเป็นตัวเลขขนาดสามสิบสองบิตสองตัว แล้วจึงตามด้วยข้อมูลขนาด \(60000\) ไบต์ แต่ละไบต์เป็นตัวเลขแทนฉลากของข้อมูลแต่ละระเบียน. ไฟล์ข้อมูลภาพ เช่น train-images.idx3-ubyte มีส่วนหัว \(16\) ไบต์ ซึ่งเป็นตัวเลขขนาดสามสิบสองบิตสี่ตัว แล้วจึงตามด้วยข้อมูลที่แต่ละไบต์เป็นตัวเลขแทนค่าความเข้มของพิกเซล (\(0\) ถึง \(255\)) เรียงกันต่อกันไป \(784\) ไบต์ต่อภาพ จำนวน \(60000\) ภาพ รวมเป็นข้อมูลภาพทั้งหมด \(47040000\) ไบต์.
ตัวอย่างคำสั่งข้างล่างนำเข้าข้อมูลฉลากของชุดฝึก
import struct
with open('train-labels.idx1-ubyte','rb') as f:
# Read header
for i in range(2):
try:
bi = f.read(4)
print('bi:', bi)
print('* little endian:', struct.unpack_from("<I",bi)[0])
print('* big endian:', struct.unpack_from(">I",bi)[0])
except struct.error:
print('error')
trainy = []
for i in range(60000):
try:
bi = f.read(1)
trainy.append(struct.unpack_from(">B",bi)[0])
except struct.error:
print('error')
trainy = np.array(trainy).reshape((1,-1))คำสั่งข้างต้นใช้คำสั่ง struct.unpack_from(">I",bi) เพื่ออ่านตัวเลข (32 บิต) ออกมา สำหรับตรวจสอบความถูกต้อง และใช้คำสั่ง struct.unpack_from(">B",bi) เพื่ออ่านข้อมูลตัวเลข (8 บิต) ออกมาเก็บรวบรวมใน trainy. รูป 18 แสดงการแจกแจงของข้อมูลเอมนิสต์.

ในลักษณะเดียวกัน ข้อมูลภาพ เช่น train-images.idx3-ubyte ก็สามารถนำเข้าเป็นตัวแปร trainx (นัมไพอาร์เรย์ สัดส่วน (784, 60000)). ข้อมูลอินพุตแต่ละระเบียน จะมี \(784\) ค่าลักษณะ. แต่ละค่าลักษณะ เป็นเลขจำนวนเต็มตั้งแต่ \(0\) ถึง \(255\). ตัวอย่างของอินพุตแต่ละระเบียน แสดงในรูป 20 ภาพซ้าย. เมื่อนำค่าลักษณะ จะจัดเรียงใหม่เป็นสองลำดับชั้นมิติ และนำไปวาดลงในภาพสองมิติ จะได้ดังแสดงในภาพขวา ซึ่งวาดด้วยคำสั่ง plt.imshow(trainx[:,9].reshape((28,28)), cmap=plt.cm.bone) ซึ่งเลือกข้อมูลภาพลำดับที่เก้ามาแสดง. ตัวอย่างภาพตัวเลขต่าง ๆ ของข้อมูลเอมนิสต์ แสดงดังรูป 21.
 |
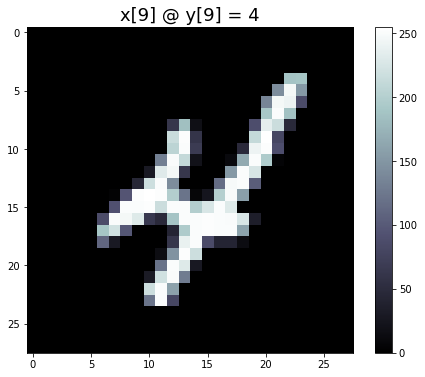 |

ภาระกิจการรู้จำตัวเลขลายมือ เป็นงานการจำแนกประเภท ที่เอาต์พุตมีค่าที่เป็นไปได้ \(10\) ฉลาก. คำสั่งข้างล่าง แสดงตัวอย่างการสร้างโครงข่ายประสาทเทียมเป็นแบบจำลองสำหรับงานรู้จำตัวเลขลายมือ โดยใช้ข้อมูลเอมนิสต์ในการฝึก.
trainxn = trainx/255 # normalize pixel [0,255] to [0,1]
trainyc = coding(trainy, onehot_cbook(10))
# Configure net
net = w_initngw([784, 8, 10])
net['act1'] = sigmoid
net['act2'] = softmax
# Train net
trained_net, train_losses = train_mlp(net, trainxn, trainyc,
cross_entropy, lr=1, epochs=300)เมื่อ trainx และ trainy เป็นข้อมูลเอมนิสต์สำหรับฝึก ที่นำเข้ามา. คำสั่ง trainxn = trainx/255 ปรับขนาดของอินพุตให้อยู่ในช่วงศูนย์ถึงหนึ่ง. ส่วนคำสั่งถัดมา ปรับเอาต์พุตให้อยู่ในรหัสหนึ่งร้อน (โปรแกรม coding และ onehot_cbook ดูแบบฝึกหัด 1.1.0.1.3). ตัวอย่างนี้ใช้โครงข่ายประสาทเทียมสองชั้น ขนาด \(8\) หน่วยซ่อน โดยโครงข่ายรับอินพุตขนาด \(784\) มิติ และให้เอาต์พุตออกมาขนาด \(10\) มิติ. ค่าน้ำหนักเริ่มต้น กำหนดด้วยวิธีเหงี่ยนวิดโดรว์ (รายการ [code: w_initngw]). ฟังก์ชันซอฟต์แมกซ์ และฟังก์ชันสูญเสียครอสเอนโทรปี ถูกเลือกใช้สำหรับภารกิจการจำแนกกลุ่ม (รายการ [code: softmax] และ [code: cross entropy]). ตัวอย่างนี้ ฝึก \(300\) สมัย โดยใช้อัตราเรียนรู้เป็น \(1\).
สังเกต โปรแกรมซอฟต์แมกซ์ เขียนโดยอาศัยคุณสมบัติคณิตศาสตร์ \[\frac{e^{a_k}}{\sum_i e^{a_i}} = \frac{e^{a_k - a_{\max}}}{\sum_i e^{a_i - a_{\max}}}
\nonumber\] เมื่อ \(a_{\max}\) คือค่าส่วนประกอบของเวกเตอร์ที่มีค่ามากที่สุด. (ทดลองรันฟังก์ชันซอฟต์แมกซ์ โดยใช้ค่า va ต่าง ๆ. ทดลองค่าใหญ่ ๆ ด้วย เช่น va = np.array([[800],[500],[100]]) สังเกตผล และเปรียบเทียบกับผลจากโปรแกรมที่แสดงในแบบฝึกหัด [ex: num nan] และอภิปราย.) ฟังก์ชันสูญเสียครอสเอนโทรปี (รายการ [code: cross entropy]) ซึ่งคือ \(-\log \hat{y}_k\) สำหรับ ทุก ๆ ค่า \(k\) ที่ทำให้ \(y_k = 1\) ก็เขียนด้วยการคำนวณ \[-\log\left( \sum_k y_k \cdot \hat{y}_k\right)\] เมื่อ \(\hat{y}_k\) คือเอาต์พุตจากแบบจำลองที่ผ่านซอฟต์แมกซ์ออกมา สำหรับกลุ่มที่ \(k^{th}\) และเอาต์พุตเฉลย \(y_k\) เป็นส่วนประกอบของฉลากในรหัสหนึ่งร้อน \(\boldsymbol{y} = [y_1, \ldots, y_K]\) เมื่อ \(K\) เป็นจำนวนกลุ่ม. นั่นคือ \(y_k \in \{0, 1\}\) และ \(\sum_{k=1}^K y_k = 1\). (อภิปราย การเขียนโปรแกรมฟังก์ชันสูญเสียครอสเอนโทรปี ดังรายการ [code: cross entropy] เปรียบเทียบกับการเขียนโปรแกรมตาม \(-\sum_k y_k \cdot \log \hat{y}_k\).) หมายเหตุ ตัวแปร yhat และ y เป็นเมทริกซ์ขนาด \(K \times N\) เมื่อ \(N\) เป็นจำนวนจุดข้อมูล และผลลัพธ์ของ cross_entropy ซึ่งคือค่าสูญเสียของจุดข้อมูลต่าง ๆ เป็นเมทริกซ์ขนาด \(1 \times N\). ดังนั้นการคำนวณค่าสูญเสียไม่สามารถเขียนในรูปเวคตอไรเซชั่นได้. โปรแกรมในรายการ [code: cross entropy] จึงเขียนด้วย -np.log(np.sum(y*yhat,axis=0)).
def softmax(va):
assert va.shape[0] > 1, 'va must be in K x N.'
amax = np.max(va, axis=0)
ap = va - amax
expa = np.exp(ap)
denom = np.sum(expa, axis=0)
return expa/denomdef cross_entropy(yhat, y):
assert yhat.shape == y.shape
eps = 1e-323
return -np.log(np.sum(y*yhat,axis=0) + eps).reshape((1,-1))หลังจากฝึกเสร็จ แบบจำลองสามารถทำไปใช้งานได้. คำสั่งข้างล่าง แสดงตัวอย่างการทดสอบแบบจำลองที่ฝึกมา
testxn = testx/255
Yp = mlp(trained_net, testxn)
Yc = np.argmax(Yp, axis=0)
accuracy = np.mean(Yc == testy[0,:])
print('Accuracy = ', accuracy)เมื่อ testx และ testy เป็นข้อมูลทดสอบ. ตัวแปร Yp เป็นเอาต์พุตของแบบจำลอง ที่อยู๋ในรูปประมาณรหัสหนึ่งร้อน ส่วน Yc คือฉลากที่ทาย โดย เลือกฉลากที่มีส่วนประกอบในรหัสหนึ่งร้อน มีค่าสูงสุด เป็นฉลากที่ทาย.
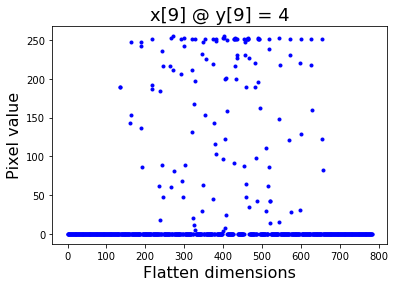
ตาราง 3 แสดง เมทริกซ์สับสน ของผลทดสอบตัวอย่างที่ได้. ตัวเลขตามแนวทะแยงมุม คือจำนวนที่ทายถูก ในแต่ละประเภท. จากเมทริกซ์สับสนในตัวอย่าง ช่วยให้การวิเคราะห์ความผิดพลาด ทำได้สะดวกขึ้น เช่น จากเมทริกซ์ ภาพตัวเลขที่ทายผิดมากที่สุด คือภาพเลขเก้า ที่ถูกทายเป็นเลขสี่ถึง \(81\) ครั้ง และในทางกลับกัน ก็มีผิดไป \(48\) ครั้ง. รูป 23 แสดงตัวอย่างรูปที่สับสนระหว่างภาพเลขสี่ และภาพเลขเก้า.
| ฉลากเฉลย | ||||||||||
| ทำนาย | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 947 | 0 | 17 | 5 | 3 | 12 | 17 | 4 | 8 | 8 |
| 1 | 1 | 1100 | 24 | 1 | 1 | 5 | 4 | 18 | 12 | 6 |
| 2 | 1 | 4 | 900 | 30 | 3 | 3 | 5 | 28 | 5 | 1 |
| 3 | 4 | 5 | 17 | 872 | 0 | 68 | 0 | 8 | 21 | 15 |
| 4 | 0 | 1 | 11 | 0 | 896 | 14 | 14 | 11 | 13 | 81 |
| 5 | 15 | 2 | 4 | 55 | 3 | 737 | 20 | 0 | 44 | 11 |
| 6 | 6 | 4 | 10 | 2 | 14 | 19 | 894 | 0 | 21 | 1 |
| 7 | 4 | 2 | 12 | 16 | 1 | 9 | 1 | 921 | 8 | 34 |
| 8 | 2 | 17 | 31 | 22 | 13 | 18 | 3 | 2 | 831 | 8 |
| 9 | 0 | 0 | 6 | 7 | 48 | 7 | 0 | 36 | 11 | 844 |
| ค่าความแม่นยำ \(89.4 \%\). | ||||||||||
[tbl: ann ex confusion matrix]
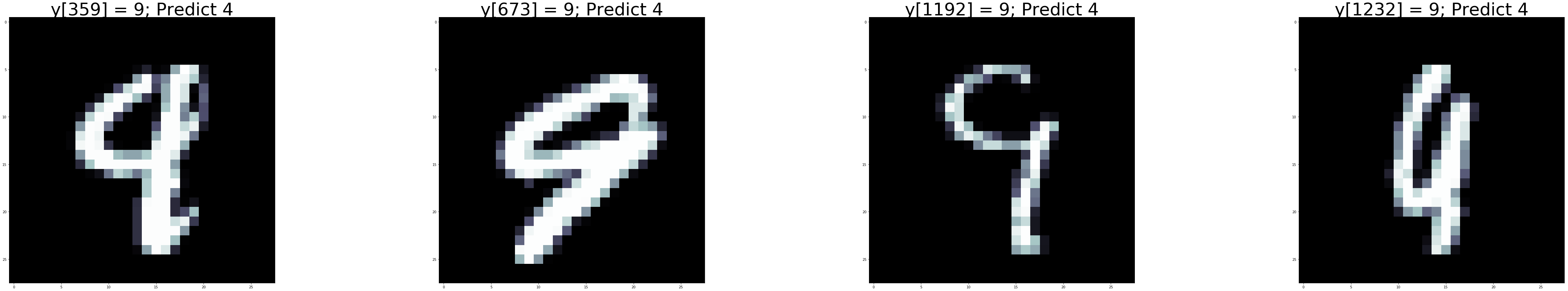
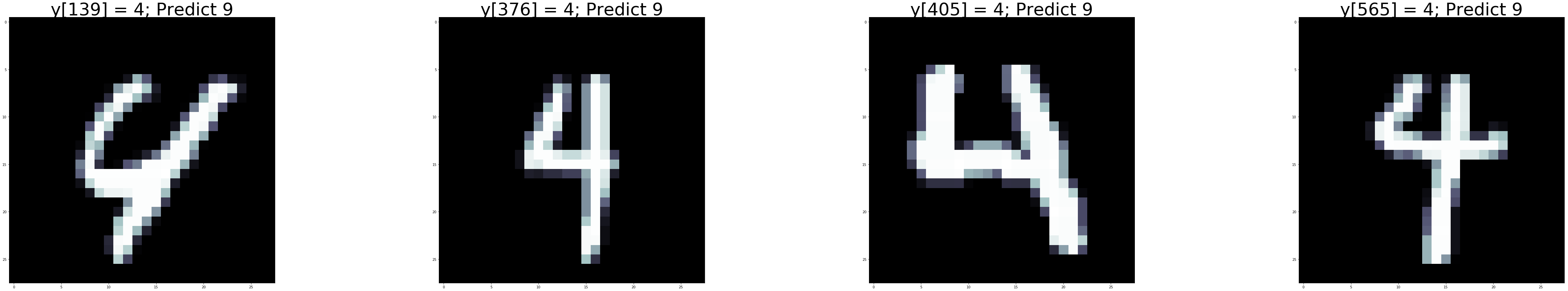
3.1.0.2.2 แบบฝึกหัด
การทำนายการจับตัวกันระหว่างโปรตีนและโมเลกุลขนาดเล็ก (protein-ligand binding prediction) เป็นภารกิจที่สำคัญในกระบวนการค้นหายา โดยเฉพาะการออกแบบยา (ดูเกร็ดความรู้การค้นหายา). แบบฝึกหัดนี้ ได้แรงบรรดาลใจจากงานศึกษา ของซานเชซและคณะ. คณะของซานเชซ ใช้ข้อมูลจากฐานข้อมูลดียูดี (DUD: A Directory of Useful Decoys http://dud.docking.org/) ที่รวบรวมข้อมูลของลิแกนต์ และตัวหลอก ของโปรตีนต่าง ๆ ซึ่งลิแกนต์ (ligand) คือโมเลกุลที่จับตัวกับโปรตีนที่สนใจ ส่วนตัวหลอก (decoy) คือโมเลกุลที่ไม่จับตัวกับโปรตีนที่สนใจ.
จงเลือกโปรตีนเป้าหมายจากฐานข้อมูลดียูดี และสร้างแบบจำลองทำนายการจับตัวกันของโปรตีนเป้าหมาย กับโมเลกุลขนาดเล็ก โดยจะสร้างเป็นแบบจำลองเฉพาะสำหรับโปรตีนนั้น และใช้คุณลักษณะต่าง ๆ ของโมเลกุลขนาดเล็ก เพื่อทำนายว่าโมเลกุลจะสามารถจับกับโปรตีนเป้าหมายได้หรือไม่. ทดสอบ วิเคราะห์ อภิปรายผล และสรุป. หมายเหตุ การสร้างแบบจำลองทั่วไปที่สามารถทำนายการจับตัวระหว่างโมเลกุลกับโปรตีนใด ๆ มีความท้าทายมาก และคู่ควรกับโครงการวิจัยระยะยาว (งานวิจัยของคณะของซานเชซเอง ก็เป็นการสร้างแบบจำลองเฉพาะกับแต่ละโปรตีน). ดังนั้น เพื่อให้เหมาะสมกับเนื้อหา ระดับความยาก และเวลา แบบฝึกหัดนี้จำกัดปัญหาเป็นการสร้างแบบจำลองเฉพาะโปรตีนก่อน.
ภารกิจนี้ มีผลทำนายเป็นสองสถานะ คือ จับตัวกัน หรือไม่จับตัวกัน. ดังนั้น ภาระกิจนี้ควรวางกรอบเป็นงานการจำแนกค่าทวิภาค. อินพุตของแบบจำลองเป็นคุณลักษณะของโมเลกุล ซึ่งคณะของซานเชซ ใช้ไลบรารี่เคโมไพ (chemopy http://code.google.com/p/pychem/downloads/list) ช่วยในการจัดเตรียมคุณลักษณะของโมเลกุล จากข้อมูลรูปแบบโมลสอง (Tripos’s mol-2 format) ที่ได้จากฐานข้อมูลดียูดี. แต่ตัวอย่างที่จะแสดงต่อไปนี้ เลือกที่จะจัดเตรียมคุณลักษณะต่าง ๆ ของโมเลกุลเอง โดยเลือกทำเฉพาะคุณลักษณะง่าย ๆ ที่ไม่ซับซ้อนจนเกินไป. ผู้อ่านอาจทดลองไลบรารี่เคโมไพ หรือไลบรารี่ที่เกี่ยวข้องอื่น ๆ เช่น อาร์ดีคิต (RDKit http://www.rdkit.org ) หากสนใจ.
ฐานข้อมูลดียูดี มีข้อมูลของโปรตีนสำคัญ ๆ อยู่หลายตัว (dud.docking.org/r2/) เช่น แอนจิโอเท็นซินคอนเวิร์ตติง เอนไซม์ (Angiotensin-converting enzyme), อะเซติลโคลีน เอสเตอเรส (Acetylcholine esterase) รวมถึง เอชเอมจี โคเอ รีดักเตส (Hydroxymethylglutaryl-CoA reductase) และไทโรซีนคิเนสซาร์ค (Tyrosine kinase SRC). ตัวอย่างต่อไปนี้ เลือกเป้าหมายเป็นโปรตีนไทโรซีนคิเนสซาร์ค ซึ่งเป็นเอนไซม์ทีี่เกี่ยวข้องกับโรคมะเร็งเนื้อเยื่อเกี่ยวพัน (sarcoma). รายการ [code: load_compounds] แสดงโปรแกรมสำหรับนำเข้าข้อมูล โดยโปรแกรมรับชื่อไฟล์ข้อมูล (พร้อมเส้นทาง) ด้วยอาร์กิวเมนต์ cpath และรีเทิร์นลิสต์ของดิกชันนารีออกมา. ลิแกนต์และตัวหลอก ถูกโหลดได้ด้วยคำสั่ง เช่น
ligands = load_compounds('databases/dud_decoys2006/src_decoys.mol2')
decoys = load_compounds('databases/dud_ligands2006/src_ligands.mol2')สำหรับโปรตีนไทโรซีนคิเนสซาร์คนี้ ข้อมูลลิแกนต์มีอยู่ \(159\) โมเลกุล และข้อมูลตัวหลอกมีอยู่ \(6319\) โมเลกุล. โมเลกุลแต่ละตัว จะมีข้อมูลอยู่สามชนิดคือ ข้อมูลทั่วไปของโมเลกุล ข้อมูลของอะตอมต่าง ๆ ในโมเลกุล และข้อมูลของพันธะที่เชื่อมอะตอมต่าง ๆ ซึ่งสามารถเข้าถึง ได้ด้วยคำสั่งเช่น ligands[0]['MOLECULE'] หรือ ligands[0]['ATOM'] หรือ ligands[0]['BOND'] สำหรับ ข้อมูลต่าง ๆ ของลิแกนต์โมเลกุลแรก (ลำดับที่ศูนย์). รูปแบบไฟล์ข้อมูลโมลสอง และคำอธิบาย สามารถศึกษาเพิ่มเติมได้จากเอกสารประกอบ Tripos Mol2 SYBYL 7.1 (Mid-2005) ที่สามารถค้นหาได้จากอินเตอร์เนต.
def load_compounds(cpath):
with open(cpath, 'r') as f:
ctxt = f.read()
field_name = 'dummy key'
v = 'dummy value'
field_count = 0
compounds = []
hasData = False
d = {}
for line in ctxt.split('\n'):
if line[:9] == '@<TRIPOS>':
field_count = 0 # start new field
if hasData:
d[field_name] = v
field_name = line[9:]
if field_name == 'MOLECULE' and hasData:
compounds.append(d)
d = {}
hasData = True
else:
if len(line) > 0:
if field_name == 'MOLECULE':
if field_count == 0:
v = {}
v['name'] = line
elif field_count == 1:
molecule_info = line.split()
v['num_atom'] = molecule_info[0]
if len(molecule_info) > 1:
v['num_bonds'] = molecule_info[1]
elif field_count == 2:
v['mol_type'] = line
elif field_count == 3:
v['charge_type'] = line
elif field_name == 'ATOM':
if field_count == 0:
v = []
atom_info = line.split()
if len(atom_info) > 5:
row = [int(atom_info[0]), # id
atom_info[1], # name
float(atom_info[2]), # x
float(atom_info[3]), # y
float(atom_info[4]), # z
*atom_info[5:]] # type and others
v.append(row)
elif field_name == 'BOND':
if field_count == 0:
v = []
bond_info = line.split()
if len(bond_info) > 3:
row = [int(bond_info[0]), # id
int(bond_info[1]), # atom1
int(bond_info[2]), # atom2
bond_info[3]] # bond_type
v.append(row)
field_count += 1
# end for line
d[field_name] = v
compounds.append(d)
return compoundsจากข้อมูลที่ได้นำเข้ามา ตัวอย่างนี้เลือกแปลงข้อมูลของโมเลกุลเป็นลักษณะสำคัญเชิงเลข โดยใช้จำนวนอะตอม จำนวนพันธะ จำนวนอะตอมคาร์บอน จำนวนอะตอมไฮโดรเจน จำนวนอะตอมออกซิเจน จำนวนอะตอมไนโตรเจน จำนวนอะตอมกำมะถัน จำนวนพันธะเดี่ยว จำนวนพันธะคู่ จำนวนพันธะสาม จำนวนพันธะเอไมด์ และ จำนวนพันธะอะโรมาติก ดังโปรแกรม compound_feat1 ในรายการ [code: compound_feat1]. ข้อมูลลิแกนต์และตัวหลอก (ตัวแปร xlig และ xdec ตามลำดับ) เตรียมได้ดังตัวอย่างคำสั่ง
xlig = np.zeros((12,0))
for c in ligands:
xi = compound_feat1(c)
xlig = np.hstack((xlig, xi))
xdec = np.zeros((12,0))
for c in decoys:
xi = compound_feat1(c)
xdec = np.hstack((xdec, xi))โปรแกรม compound_feat1 เรียกใช้ count_elements และ count_bonds ซึ่งแสดงในรายการ [code: bind affin count].
def compound_feat1(c):
feat = np.zeros((12, 1))
feat[0] = c['MOLECULE']['num_atom']
feat[1] = c['MOLECULE']['num_bonds']
celements = count_elements(c)
feat[2] = celements['C']
feat[3] = celements['H']
if 'O' in celements.keys():
feat[4] = celements['O']
if 'N' in celements.keys():
feat[5] = celements['N']
if 'S' in celements.keys():
feat[6] = celements['S']
cbonds = count_bonds(c)
feat[7] = cbonds['1']
feat[8] = cbonds['2']
feat[9] = cbonds['3']
feat[10] = cbonds['am']
feat[11] = cbonds['ar']
return featimport re
def count_elements(c):
elements = {}
for r in c['ATOM']:
mr = re.match('[A-Za-z]+', r[1])
if not mr:
print('No element!', r[1])
continue
else:
e = mr.group(0)
if e not in elements.keys():
elements[e] = 1
else:
elements[e] += 1
return elements
def count_bonds(c):
bonds = {'1': 0, '2': 0, '3': 0, 'am': 0, 'ar': 0}
for b in c['BOND']:
bond_type = b[3]
if bond_type in bonds.keys():
bonds[bond_type] += 1
else:
print('undefined bond:', bond_type)
return bondsเนื่องจากสัดส่วนจำนวนข้อมูลลิแกนต์ ต่างจากจำนวนข้อมูลตัวหลอกมาก ตัวอย่างคำสั่งข้างล่าง แบ่งข้อมูลประมาณ \(60\%\) สำหรับการฝึก และที่เหลือสำหรับการทดสอบ แล้วรวมข้อมูลลิแกนต์และตัวหลอกเข้าด้วยกัน
_, Nlig = xlig.shape
_, Ndec = xdec.shape
ids_lig = np.random.choice(Nlig, Nlig, replace=False)
ids_dec = np.random.choice(Ndec, Ndec, replace=False)
mark_lig = round(Nlig * 0.6)
trainx_lig = xlig[:, ids_lig[:mark_lig]]
testx_lig = xlig[:, ids_lig[mark_lig:]]
mark_dec = round(Ndec * 0.6)
trainx_dec = xdec[:, ids_dec[:mark_dec]]
testx_dec = xdec[:, ids_dec[mark_dec:]]
# Combine ligands and decoys
_, N1 = trainx_lig.shape
_, N0 = trainx_dec.shape
trainx = np.hstack((trainx_lig, trainx_dec))
trainy = np.hstack((np.ones((1, N1)), np.zeros((1, N0))))
_, N1 = testx_lig.shape
_, N0 = testx_dec.shape
testx = np.hstack((testx_lig, testx_dec))
testy = np.hstack((np.ones((1, N1)), np.zeros((1, N0))))![fig: การแจกแจงของลักษณะสำคัญเชิงเลข ทั้ง 12 ลักษณะสำคัญ (x[0] ถึง x[11]) ของข้อมูลโมเลกุลสารประกอบทั้งลิแกนต์ (y=1) และตัวหลอก (y=0).](03Ann/ligand/train_data1.png)
![fig: การแจกแจงของลักษณะสำคัญเชิงเลข ทั้ง 12 ลักษณะสำคัญ (x[0] ถึง x[11]) ของข้อมูลโมเลกุลสารประกอบทั้งลิแกนต์ (y=1) และตัวหลอก (y=0).](03Ann/ligand/train_data2.png)
![fig: การแจกแจงของลักษณะสำคัญเชิงเลข ทั้ง 12 ลักษณะสำคัญ (x[0] ถึง x[11]) ของข้อมูลโมเลกุลสารประกอบทั้งลิแกนต์ (y=1) และตัวหลอก (y=0).](03Ann/ligand/train_data3.png)
รูป 26 แสดงการแจกแจงของข้อมูลฝึก. ค่าอินพุตมีช่วงค่อนข้างกว้าง คำสั่งข้างล่างแสดงตัวอย่างการทำนอร์มอไลซ์อินพุต เตรียมแบบจำลองโครงข่ายประสาทเทียมสองชั้นขนาด \(8\) หน่วยซ่อน และฝึก \(500\) สมัยด้วยอัตราเรียนรู้ \(0.1\).
trainxn, normpars = normalize2(trainx)
num_epochs = 500
learn_rate = 0.1
net = w_initn([12, 8, 1])
net['act1'] = sigmoid
net['act2'] = sigmoid
trained_net, train_losses = train_mlp(net, trainxn, trainy,
binaries_cross_entropy, lr=learn_rate, epochs=num_epochs)ตัวอย่างคำสั่งข้างล่างทำการทดสอบผลการทำนาย
testxn, _ = normalize2(testx, normpars)
Yp = mlp(trained_net, testxn)
Yc = cutoff(Yp)
accuracy = np.mean(Yc == testy)ผลลัพธ์ของตัวอย่าง แสดงค่าความแม่นยำออกมาที่ \(97.5\%\). หมายเหตุ ผลลัพธ์ที่ทดลองแต่ละครั้งอาจแสดงค่าที่ต่างกันไปเนื่องจากผลของการสุ่ม ซึ่งอยู่ในกระบวนการแบ่งข้อมูล และการกำหนดค่าน้ำหนักเริ่มต้น. ดังนั้น หากต้องการศึกษาปัจจัยที่เกี่ยวข้องอย่างสมบูรณ์ ควรทำการทดลองซ้ำ โดยให้จำนวนทำซ้ำมากพอ 1 เพื่อยืนยันผลว่าความต่างของผลลัพธ์เป็นผลมาจากปัจจัยที่ต่างกันจริง ๆ ไม่ใช่มาจากความแปรปรวนของข้อมูลหรือความแปรปรวนจากกระบวนการสุ่ม. แต่เพื่อความกระชับ ตัวอย่างนี้ไม่ได้ทำซ้ำ.
ค่าความแม่นยำที่ได้ แม้จะดูดีมาก แต่เมื่อพิจารณาเมทริกซ์ความสับสนที่ได้ (ดังแสดงข้างล่าง) แล้วจะพบว่าแบบจำลองนี้ล้มเหลว เพราะมันไม่ระบุสารประกอบใดที่อาจจับตัวกับเป้าหมายเลย.
| ผลจริง | |||
| 1 | 0 | ||
| จำนวนบวกจริง | จำนวนบวกเท็จ | ||
| ผลทำนาย | 1 | 0 | 0 |
| จำนวนลบเท็จ | จำนวนลบจริง | ||
| 0 | 64 | 2528 | |
สังเกตว่า เมื่อสัดส่วนจำนวนข้อมูลต่างกันมาก แบบจำลองเพียงทำนายว่า ไม่จับตัวกับเป้าหมาย กับทุก ๆ สารประกอบ ก็สามารถจะได้ค่าความแม่นยำที่สูงมากได้. แต่เมื่อพิจารณาค่าความเที่ยงตรง และค่าการระลึกกลับ ซึ่งเป็น \(0/0\) และ \(0\) ตามลำดับ จะพบว่า ความเที่ยงตรง และการระลึกกลับ สะท้อนความล้มเหลวของแบบจำลองทำนายได้ชัดเจนมาก.
ก่อนจะอภิปรายเรื่องวิธีจัดการกับปัญหาสัดส่วนจำนวนข้อมูลไม่สมดุล พิจารณาค่าเอาต์พุตที่ได้จากแบบจำลอง สำหรับกรณีของลิแกนต์และตัวหลอก. รูป 27 แสดงให้เห็นว่า ค่าเอาต์พุตที่มากที่สุด มีค่าอยู่แค่ประมาณ \(0.2\). ค่าเอาต์พุตที่ได้จะถูกตัดสินใจสุดท้ายด้วย โปรแกรม cutoff (ดูแบบฝึกหัด 1.1.0.1.3) ที่ค่าดีฟอล์ตคือตัดทายหนึ่งที่ \(0.5\). ดังนั้น ค่าใด ๆ ที่น้อยกว่า \(0.5\) จะทายเป็นศูนย์ และทำให้ทุก ๆ สารประกอบ ถูกทายเป็นศูนย์ (หรือทายว่าไม่จับตัวกับเป้าหมาย). แต่เมื่อพิจารณารูป 27 โดยเฉพาะค่าความต่างระหว่างเอาต์พุตที่ได้สำหรับลิแกนต์ เปรียบเทียบกับตัวหลอก จะพบว่า แม้ทั้งคู่จะมีค่าต่ำ แต่ค่าเอาต์พุตสำหรับลิแกนต์ส่วนใหญ่ ก็มากกว่าค่าเอาต์พุตสำหรับตัวหลอก ค่อนข้างชัดเจน. ดังนั้น ความล้มเหลวของการทำนายนี้ อาจบรรเทาได้เพียงแค่การปรับระดับค่าขีดแบ่ง (threshold) ลง.
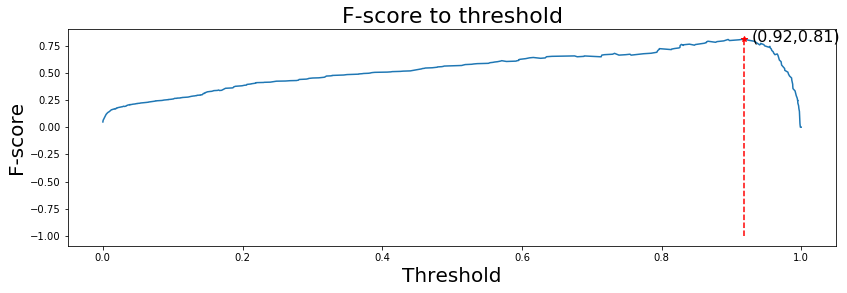
พฤติกรรมการทำนายของแบบจำลองจำแนกค่าทวิภาค สามารถถูกปรับแต่งได้จากการปรับระดับค่าขีดแบ่ง. รูป 28 แสดงค่าคะแนนเอฟ เมื่อใช้ระดับค่าขีดแบ่งต่าง ๆ. หมายเหตุ เพื่อลดความยุ่งยากจากกรณี \(0/0\) ตัวหารของค่าความเที่ยงตรง และค่าคะแนนเอฟ คำนวณด้วยคำสั่งดังตัวอย่าง
Precision = TP/(TP + FP + 1e-12)
fscore = 2 * Precision * Recall /(Precision + Recall + 1e-12)เมื่อ TP, FP, และ Recall เป็นจำนวนบวกจริง, จำนวนบวกเท็จ, และค่าการระลึกกลับ ตามลำดับ. ค่า 1e-12 เป็นค่าน้อย ๆ ที่เพิ่มเข้าไป ซึ่งจะเปลี่ยนกรณี \(0/0\) เป็น \(0\) และไม่รบกวนกรณีอื่นๆมาก.


จากรูป 28 ค่าคะแนนเอฟจะสูงสุด เมื่อเลือกใช้ระดับค่าขีดแบ่งประมาณ \(0.05\) และเมื่อเลือกระดับค่าขีดแบ่งที่ประมาณ \(0.05\) แล้วจะได้ผลทดสอบดังเมทริกซ์ความสับสน
| ผลจริง | |||
| 1 | 0 | ||
| จำนวนบวกจริง | จำนวนบวกเท็จ | ||
| ผลทำนาย | 1 | 45 | 384 |
| จำนวนลบเท็จ | จำนวนลบจริง | ||
| 0 | 19 | 2144 | |
และได้ค่าความเที่ยงตรง \(0.105\) ค่าการระลึกกลับ \(0.703\) และค่าคะแนนเอฟ \(0.183\). ผลลัพธ์ที่ได้ แม้จะยังแย่ แต่ก็ดีขึ้นกว่าเดิมมาก. นอกจากนั้น ระดับค่าขีดแบ่ง ก็สามารถเลือกปรับใช้ให้เหมาะกับความชอบส่วนบุคคล หรือให้เหมาะกับสถานการณ์ได้ เช่น บางภาระกิจ อาจเลือก บวกเท็จดีกว่าลบเท็จ (เช่น หากทรัพยากรเพียงพอ ได้ตัวหลอกเกินมา ดีกว่าขาดลิแกนต์ไป) ในขณะที่บางภาระกิจ อาจเลือก ลบเท็จดีกว่าบวกเท็จ (เช่น เมื่อทรัพยากรจำกัดมาก ๆ ตกลิแกนต์ไปบ้าง ดีกว่าได้ตัวหลอกมา และเปลืองค่าใช้จ่ายในขั้นตอนการพัฒนายาต่อไปเปล่า ๆ). เนื่องจากการเลือกระดับค่าขีดแบ่ง มีผลต่อการทำนายมาก และยังอาจถูกปรับให้เหมาะกับความชอบส่วนบุคคลได้ การประเมินแบบจำลอง บางครั้งจึงนิยมใช้กราฟอาร์โอซี (Receiver Operating Characteristic คำย่อ ROC) และพื้นที่ใต้เส้นโค้ง (Area Under Curve คำย่อ AUC). กราฟอาร์โอซี หมายถึง กราฟแสดงผลการทำนาย โดยอาจเลือกใช้ดัชนีวัดได้หลายแบบ เช่น อาจใช้กราฟระหว่างค่าความเที่ยงตรงกับค่าการระลึกกลับ (precision-recall plot) หรืออาจใช้กราฟระหว่างค่าอัตราการตรวจจับได้กับอัตราสัญญาณหลอก (detection-rate-to-false-alarm-rate plot). อัตราการตรวจจับได้ อาจเรียกว่าค่าความไว (sensitivity หรือ true positive rate) \(S_1 = \mathrm{Recall} = TP/(TP + FN)\) เมื่อ \(TP\) และ \(FN\) คือจำนวนบวกจริง และจำนวนลบเท็จ ตามลำดับ. อัตราสัญญาณหลอก (false alarm rate) \(FAR = FP/(TN + FP)\) หรือ \(FAR = 1 - S_2\) เมื่อ \(S_2\) คือค่าความจำเพาะ (specificity หรือ true negative rate) ซึ่ง \(S_2 = TN/(TN + FP)\) โดย \(TN\) และ \(FP\) คือจำนวนลบจริง และจำนวนบวกเท็จ ตามลำดับ.
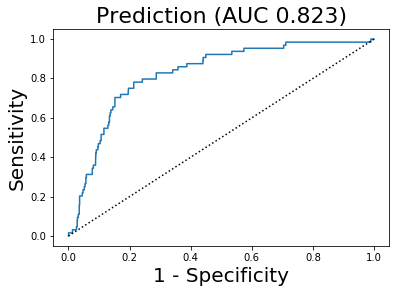
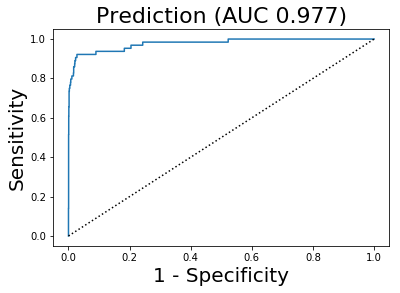
รูป 29 แสดงกราฟระหว่างค่าความไวกับอัตราสัญญาณหลอก จากผลตัวอย่าง. จุดต่าง ๆ บนเส้นกราฟคำนวณโดยการปรับระดับค่าขีดแบ่งจากน้อยที่สุดไปมากที่สุด และประเมินผลการทำนายสำหรับแต่ละระดับค่าขีดแบ่ง. พื้นที่ใต้เส้นโค้ง ก็คือพื้นที่ใต้กราฟอาร์โอซีที่เลือกใช้. รูป 29 แสดงค่าพื้นที่ใต้เส้นโค้ง กำกับไว้เหนือภาพ. ค่าพื้นที่ใต้เส้นโค้งที่ใกล้หนึ่ง แสดงถึงคุณภาพการทำนายที่ดีของแบบจำลอง.
สำหรับภารกิจการจำแนกค่าทวิภาค หรือการจำแนกกลุ่ม เมื่อจำนวนจุดข้อมูลของแต่ละกลุ่มข้อมูลต่างกันมาก จะเกิดปัญหาสัดส่วนจำนวนข้อมูลไม่สมดุล (unbalanced data) ขึ้น. วิธีจัดการปัญหาสัดส่วนจำนวนข้อมูลไม่สมดุลในชุดข้อมูลฝึก สามารถทำได้หลายวิธี เช่น วิธีการสุ่มเกิน (over sampling), วิธีการสุ่มขาด (under sampling), วิธีปรับฟังก์ชันจุดประสงค์. วิธีการสุ่มเกิน ใช้การสุ่มแบบคืนที่ (sampling with replacement) เพื่อเพิ่มจุดข้อมูลของกลุ่มน้อยขึ้นมาให้ใกล้เคียงกับกลุ่มใหญ่. วิธีการสุ่มขาด ใช้การสุ่มเลือกบางส่วนของข้อมูลจากกลุ่มใหญ่ เพื่อให้ข้อมูลของที่ใช้ฝึกของกลุ่มใหญ่มีจำนวนใกล้เคียงกับจำนวนของกลุ่มน้อย. วิธีีปรับฟังก์ชันจุดประสงค์ ปรับการคำนวณค่าฟังก์ชันจุดประสงค์ โดยให้น้ำหนักความสำคัญกับการทำนายกลุ่มน้อยมากขึ้น (หรือลดน้ำหนักความสำคัญของการทำนายกลุ่มใหญ่ลง หรือทำทั้งสองทาง) เพื่อชดเชยกับจำนวนข้อมูลที่ต่างกัน.
ตัวอย่างที่จะแสดงต่อไปนี้ ใช้วิธีการสุ่มเกิน ซึ่งสัดส่วนความต่างกันของจำนวนข้อมูลทั้งสองกลุ่ม คือ \(3791/95 \approx 40\) เท่า เมื่อ \(3791\) และ \(95\) คือจำนวนจุดข้อมูลในชุดฝึกของกลุ่มใหญ่ (ตัวหลอก) และของกลุ่มน้อย (ลิแกนต์) ตามลำดับ. ตัวอย่างนี้ เลือกเพิ่มจำนวนในกลุ่มน้อยขึ้นมาเป็นประมาณ \(80\%\) ของจำนวนในกลุ่มใหญ่ ดังแสดงในคำสั่งข้างล่าง
over_factor = int(np.floor(N0/N1 * 0.8))
ids = np.random.choice(N1, over_factor * N1, replace=True)
trainx = np.hstack((trainx_lig[:, ids], trainx_dec))
trainy = np.hstack((np.ones((1, over_factor*N1)), np.zeros((1, N0))))เมื่อ N0 คือจำนวนข้อมูลฝึกในกลุ่มใหญ่ และ N1 คือจำนวนข้อมูลฝึกในกลุ่มน้อย. ตัวแปร trainx_lig และ trainx_dec คือตัวแปรค่าอินพุตของข้อมูลกลุ่มน้อย และของข้อมูลกลุ่มใหญ่ ตามลำดับ. ฉลากเฉลยของข้อมูลลิแกนต์ กำหนดให้มีค่าเป็นหนึ่ง (ลิแกนต์ คือสารประกอบที่จับตัวกับโปรตีนเป้าหมาย) และฉลากเฉลยของข้อมูลตัวหลอก กำหนดให้มีค่าเป็นศูนย์ (ตัวหลอก คือสารประกอบที่ไม่จับตัวกับโปรตีนเป้าหมาย). ข้อมูลฝึกหลังทำการสุ่มเกินเพื่อปรับเพิ่มจำนวนข้อมูลกลุ่มน้อย คือ trainx (อินพุต) และ trainy (เอาต์พุต เฉลย).
หลังจากทำการนอร์มอไลซ์อินพุต ฝึกแบบจำลอง 2 และทดสอบแล้ว ผลที่ได้แสดงดังเมทริกซ์ความสับสน
| ผลจริง | |||
| 1 | 0 | ||
| จำนวนบวกจริง | จำนวนบวกเท็จ | ||
| ผลทำนาย | 1 | 59 | 87 |
| จำนวนลบเท็จ | จำนวนลบจริง | ||
| 0 | 5 | 2441 | |
ค่าความเที่ยงตรง \(0.404\) ค่าการระลึกกลับ \(0.922\) และค่าคะแนนเอฟ \(0.562\) ซึ่งปรับปรุงขึ้นมาก. ผลประเมินนี้ได้จากการตัดสินผลทำนายด้วยระดับค่าขีดแบ่ง \(0.5\). ในลักษณะเดียวกัน รูป 30 แสดงแผนภูมิกล่องของค่าเอาต์พุตจากแบบจำลอง สำหรับข้อมูลกลุ่มน้อย และกลุ่มใหญ่. สังเกตว่า เอาต์พุตจากแบบจำลอง มีช่วงค่าแยกกันชัดเจนมากระหว่างข้อมูลกลุ่มน้อย (ค่าใกล้หนึ่ง) และข้อมูลกลุ่มใหญ่ (ค่าใกล้ศูนย์) แม้จะมีค่าผิดปกติบ้าง. ในทางสถิติ ค่าผิดปกติ (outliers) หมายถึง ค่าของจุดข้อมูลจำนวนน้อย ที่มีค่าต่างจากค่าของจุดข้อมูลอื่น ๆ ในกลุ่มอย่างมาก.

จากรูป 30 การตัดสินผลทำนาย อาจสามารถปรับปรุงได้ง่าย ๆ ด้วยการเปลี่ยนระดับค่าขีดแบ่ง. พิจารณารูป 31 ซึ่งแสดงค่าคะแนนเอฟ ที่ระดับค่าขีดแบ่งต่าง ๆ และเมื่อเปลี่ยนระดับค่าขีดแบ่งเป็นประมาณ \(0.92\) จะได้เมทริกซ์ความสับสน
| ผลจริง | |||
| 1 | 0 | ||
| จำนวนบวกจริง | จำนวนบวกเท็จ | ||
| ผลทำนาย | 1 | 47 | 5 |
| จำนวนลบเท็จ | จำนวนลบจริง | ||
| 0 | 17 | 2523 | |
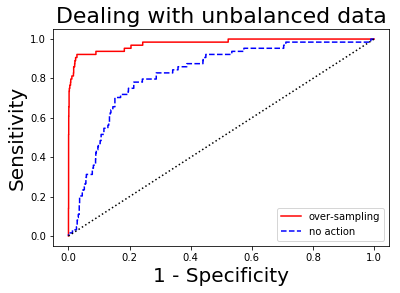
ค่าความเที่ยงตรง \(0.904\) ค่าการระลึกกลับ \(0.734\) และค่าคะแนนเอฟ \(0.810\) ซึ่งโดยทั่วไปแล้ว ค่าคะแนนเอฟขนาดนี้ ถือว่าแบบจำลองสามารถทำงานได้ดีพอสมควร. รูป 33 แสดงแสดงกราฟระหว่างค่าความไวกับอัตราสัญญาณหลอก พร้อมค่าพื้นที่ใต้เส้นโค้ง เมื่อใช้วิธีสุ่มเกิน (ภาพซ้าย) และเปรียบเทียบกับการไม่ทำอะไรเลย (ภาพขวา). จากตัวอย่างข้างต้น วิธีสุ่มเกินสามารถช่วยปรับปรุงคุณภาพของการเตรียมแบบจำลองทำนาย ในกรณีจำนวนข้อมูลไม่สมดุลได้อย่างชัดเจน.
 |
 |
3.1.0.3 เกร็ดความรู้การค้นหายา
(เรียบเรียงจาก และ และ ) ยา โดยทั่วไปคือ โมเลกุลที่กระตุ้นหรือยับยั้งการทำงานของชีวโมเลกุล เช่น โปรตีน ซึ่งส่งผลทางการรักษาโรคกับผู้ป่วย. แนวทางในการค้นหายาแบบดั้งเดิม อาจจะเริ่มด้วยการหาส่วนผสมออกฤทธิ์ (active ingredient) จากตำรับยาดั่งเดิม เช่น ยารีเซอร์พีน. รีเซอร์พีน (Reserpine) เป็นยาสำหรับบำบัดอาการความดันสูง ที่สะกัดจากรากของต้นระย่อมน้อย (Rauvolfia serpentina หรือชื่อสามัญ Indian snakeroot) ที่อยู่ในตำรับยาอายุรเวทของอินเดียมาแต่โบราณ. หรืออาจจะเริ่มด้วยการค้นหาสารประกอบต่าง ๆ ที่ส่งผลที่ต้องการ จากการทดลองกับสัตว์ที่ป่วยเป็นโรค หรือจากการทดลองในหลอดทดลองกับเซลล์ที่เป็นโรค. สารประกอบที่พบจากการค้นหาเบื้องต้น จะเรียกว่า สารประกอบหลัก. สารประกอบหลัก (lead compounds) คือ สารประกอบที่จากการทดลองแล้วพบว่าน่าจะช่วยรักษาโรคได้ แต่โครงสร้างทางเคมีอาจจะยังไม่ดีเท่าไร. จากนั้น สารประกอบหลักต่าง ๆ ที่ได้ จะถูกดัดแปลงทางเคมี เพื่อปรับปรุง การออกฤทธิ์ (potency) และสมรรถนะการเลือก (selectivity) รวมถึงปรับปรุงคุณสมบัติทางเภสัชจลนศาสตร์อื่น ๆ ให้เหมาะสมที่จะเป็นยา และสามารถดำเนินการทดสอบกับสัตว์ทดลอง และทดสอบทางคลีนิคได้ต่อไป. แนวทางในการค้นหายาแบบดั้งเดิมนี้ เริ่มจากการค้นหาสารประกอบหลักโดยสังเกตผลที่ได้โดยตรง และเมื่อพบสารประกอบหลักต่าง ๆ แล้วจึงค่อยศึกษากลไกการทำงาน และชีวโมเลกุลต่าง ๆ ที่เกี่ยวข้องกับการทำงานของสารประกอบเหล่านั้น และนำความรู้ความเข้าใจที่ได้ กลับมาปรับปรุงโครงสร้างของสารประกอบหลัก เพื่อให้ได้สารประกอบที่มีคุณสมบัติทางยาที่ดีมากขึ้น. แต่แนวทางการพัฒนายา เช่น กลีเวค ที่อภิปรายไปในเกร็ดความรู้ รูปแบบของลูคีเมียและยารักษา ดำเนินการกลับกัน คือ เริ่มจากการเข้าใจกลไกของโรค และวิถีที่เกี่ยวข้อง (biological pathway). จากนั้น เลือกชีวโมเลกุลในวิถีที่เกี่ยวข้องกับโรค เป็นเป้าหมาย. แล้วจึงออกแบบลิแกนต์หรือโมเลกุลของสารประกอบที่จะเข้าไปจับกับชีวโมเลกุลเป้าหมาย เพื่อปรับการทำงานของโมเลกุลเป้าหมายในทางรักษาบรรเทาโรค. แนวทางหลังนี้ อาจเรียกว่า การค้นหายาแบบย้อนกลับ (reverse drug discovery) หรือ การค้นหายาโดยกำหนดเป้าหมาย (target-based drug discovery).
การค้นหายาโดยกำหนดเป้าหมาย โรคหัวใจ คอเลสเตอรอล และกลุ่มยาสแตติน. แนวทางการค้นหายาโดยกำหนดเป้าหมาย เริ่มที่การเข้าใจกลไกของการทำงานของร่างกายและกลไกของโรค หรือเข้าใจเหตุก่อน. จากนั้นเลือกเป้าหมายที่อยู่ในกลไก ซึ่งอาจเป็นโปรตีน หรือดีเอ็นเอ หรืออาร์เอ็นเอ แล้วจึงหาลิแกนต์ ซึ่งคือโมเลกุลจะเข้าไปจับกับเป้าหมาย และเปลี่ยนการทำงานของเป้าหมาย ในทางที่จะช่วยแก้ไขกลไกที่เป็นเหตุของโรค. การค้นพบกลุ่มยาสแตติน (Statins) เป็นตัวอย่างหนึ่งของการค้นพบยาโดยกำหนดเป้าหมาย.
หลังสงครามโลกครั้งที่สองสงบ ยุโรปหลังสงครามลำบากมาก ขาดแคลนแทบทุกอย่าง แต่ อันเซิล คีส์ (Ancel Keys) นักผจญภัยและนักวิทยาศาสตร์ จากมินนิโซตา สหรัฐอเมริกา พบสถิติที่น่าสนใจ คือ สถิติการตายด้วยโรคหัวใจในยุโรปหลังสงครามลดลงอย่างมาก ขณะที่สถิติในอเมริกาสูงมาก. คีส์สงสัย และศึกษาว่าอะไรเป็นปัจจัยต่อการตายด้วยโรคหัวใจ นอกจากนั้น ระหว่างท่องเที่ยว คีส์พบว่า ชาวประมงในเนเปิ้ล อิตาลี มีระดับคอเลสเตอรอลในกระแสเลือดต่ำกว่าระดับคอเลสเตอรอลของนักธุรกิจอเมริกันมาก ๆ. จากข้อมูลที่เห็น คีส์เชื่อเลยว่า คนรวยกินอาหารที่อุดมด้วยไขมัน และก็หัวใจวายมากกว่า. แต่ตอนนั้น ส่วนใหญ่ไม่ได้เชื่อแบบคีส์.
ถึงแม้ว่าก่อนหน้านั้น มีงานศึกษาที่พบว่า หลอดเลือดแดงใหญ่จากเนื้อเยื้อผู้ป่วยโรคท่อเลือดแดงและหลอดเลือดแดงแข็ง มีคอเลสเตอรอลมากกว่าที่เนื้อเยื้อปกติมี ถึงกว่ายี่สิบเท่า และถ้าให้สัตว์กินคอเลสเตอรอลมาก ๆ แล้วมันจะป่วยเป็นโรคภาวะไขมันในเลือดสูง และโรคท่อเลือดแดงและหลอดเลือดแดงแข็ง แต่คนส่วนใหญ่ก็ยังไม่ค่อยมั่นใจเท่าไรว่า อาหาร ระดับคอเลสเตอรอลในกระแสเลือด และโรคหัวใจ มันเกี่ยวข้องกัน. ดังนั้น คีส์และเพื่อนนักวิจัย ได้ร่วมกันทำโครงการวิจัยระดับนานาชาติ เพื่อศึกษาปัจจัยความเสี่ยงต่ออาการหัวใจวาย โดยครอบคลุมกลุ่มตัวอย่างมากกว่า \(12,000\) คน จากที่ต่าง ๆ ของโลก ยูโกสลาเวีย อิตาลี กรีก ฟินแลนด์ เนเธอร์แลนด์ ญี่ปุ่น และสหรัฐอเมริกา ซึ่งแต่ละที่มีวัฒนธรรมอาหารการกินที่แต่ต่างกันมาก. ผลการศึกษาพบ ความสัมพันธ์ระหว่างอาหารที่กินกับระดับคอเลสเตอรอลในกระแสเลือด และยืนยันว่า ระดับคอเลสเตอรอลในกระแสเลือดเป็นปัจจัยเสี่ยงหลักต่อการเป็นโรคหัวใจ คนที่มีระดับคอเลสเตอรอลในกระแสเลือดสูงกว่า \(260\) มิลลิกรัมต่อเดซิลิตร จะมีโอกาสที่จะหัวใจวายเป็นห้าเท่าของคนที่มีระดับคอเลสเตอรอลในกระแสเลือดต่ำกว่า \(200\) มิลลิกรัมต่อเดซิลิตร.
สิ่งหนึ่งที่ควรระลึก คือ เช่นเดียวกับหลาย ๆ อย่างในธรรมชาติและชีวิต ไม่มีอะไรที่ดีหรือชั่วโดยสมบูรณ์. คอเลสเตอรอลไม่ใช่สิ่งชั่วร้าย น่ารังเกียจ ที่ต้องกำจัดออกไปให้สิ้นซาก ถอนรากถอนโคน. คอเลสเตอรอลเป็นสิ่งที่จำเป็นกับชีวิต ร่างกายเราต้องการคอเลสเตอรอล คอเลสเตอรอลเป็นส่วนประกอบสำคัญของเยื่อหุ้มเซลล์ในเซลล์ของสัตว์ทุกชนิด (รวมถึงเซลล์ของเราด้วย). คอเลสเตอรอลไม่ได้ชั่วร้าย เพียงแต่ ปริมาณของมันที่เกินระดับ จะสร้างปัญหา.
“All things are poison, and nothing is without poison, the dosage alone makes it so a thing is not a poison.”
—Paracelsus
“ทุกสิ่งล้วนเป็นพิษ ไม่มีสิ่งใดปราศจากพิษ ปริมาณเท่านั้นที่จะทำให้ไม่เป็นพิษ.”
—พาราเซลซุส
ช่วงปี ค.ศ. 1969-1970 ระหว่างที่นายแพทย์โจเซฟ โกลด์สไตน์ (Joe Goldstein) ทำงานที่โรงพยาบาลของสถาบันหัวใจแห่งชาติ (National Heart Institute) ในเมืองเบเธสดา รัฐแมรี่แลนด์ สหรัฐอเมริกา โกลด์สไตน์ได้ดูแลคนไข้เด็กสองคนที่ป่วยเป็นโรคภาวะไขมันในเลือดสูงทางพันธุกรรม (familial hypercholesterolemia คำย่อ FH). เด็กทั้งสองเป็นพี่น้องกัน อายุแค่หกขวบกับแปดขวบเท่านั้น แต่มีคอเลสเตอรอลในเลือดอยู่ในระดับสูงมาก คืออยู่ในช่วง \(800\) มิลลิกรัมต่อเดซิลิตร.
โกลด์สไตน์สนใจกรณีนี้มาก และศึกษากรณีนี้ร่วมกับไมเคิล บราวน์ (Michael Brown). ตอนนั้นในวงการแพทย์รู้อยู่แล้วว่า ร่างกายมีการสังเคราะห์คอเลสเตอรอล และการสังเคราะห์คอเลสเตอรอลเป็นกลไกการควบคุมแบบป้อนกลับ นั่นคือ ถ้าให้อาหารที่มีคอเลสเตอรอลสูงกับสุนัข ร่างกายของสุนัขนั้นจะหยุดการสังเคราะห์คอเลสเตอรอลลง. ความรู้นี้ ทำให้โกลด์สไตน์และบราวน์สงสัยว่า เด็กทั้งสองอาจจะมีการผิดปกติในกลไกการควบคุมแบบป้อนกลับนี้.
ขณะที่เพื่อน ๆ ของโกลด์สไตน์และบราวน์ ส่วนใหญ่ศึกษาเรื่องมะเร็ง หรือประสาทวิทยา หรือเรื่องอื่น ๆ ที่อยู่ในกระแส แต่ทั้งโกลด์สไตน์และบราวน์ ตัดสินใจที่จะศึกษาเรื่องกลไกควบคุมคอเลสเตอรอลอย่างจริงจัง ถึงแม้เพื่อน ๆ ของเขาจะชอบล้อเลียนว่า “มันก็แค่ก้อนหยุ่ ๆ ไร้รูปร่าง” โกลด์สไตน์และบราวน์ ได้ทำงานร่วมกันอย่างเป็นทางการ หลังจากทั้งคู่ย้ายไปศูนย์การแพทย์ตะวันตกเฉียงใต้มหาวิทยาลัยเท็กซัส. ระหว่างสองปีที่ทั้งคู่มุ่งมั่นทำงานหนัก ปริศนากลไกควบคุมคอเลสเตอรอลก็เฉลย.
โกลด์สไตน์และบราวน์ เริ่มสืบจากวิถีการสังเคราะห์คอเลสเตอรอลที่วงการแพทย์ตอนนั้นรู้ดีอยู่แล้ว. ทั้งคู่มุ่งความสนใจที่อัตราการสังเคราะห์คอเลสเตอรอล ซึ่งจะขึ้นกับเอนไซม์ในขั้นแรกของวิถี ที่ชื่อ เอชเอมจี โคเอ รีดักเตส (HMG-CoA reductase หรือ 3-hydroxy-3-methyl-glutaryl-coenzyme A reductase) ซึ่งจะเรียกสั้น ๆ ว่า รีดักเตส. ถ้ารีดักเตสทำงานมาก คอเลสเตอรอลจะถูกสังเคราะห์ออกมามาก.
การทำงานของรีดักเตส จะอยู่ที่ตับ เพราะฉะนั้น โกลด์สไตน์และบราวน์ไม่สามารถศึกษาการทำงานของรีดักเตสโดยตรงได้. ทั้งคู่ตัดสินใจ ศึกษาการทำงานของรีดักเตสจากเซลล์ที่ตัดและนำมาเพาะเลี้ยงไว้แทน. เซลล์ที่เพาะเลี้ยงในหลอดทดลอง ต้องการสารอาหารที่จะป้อนให้ในรูปซีรัม (serum ซึ่งเป็นน้ำเลือดที่ไม่มีเม็ดเลือด). โกลด์สไตน์และบราวน์ สังเกตว่าการทำงานของรีดักเตสถูกควบคุมจากอะไรบางอย่างในซีรัม คือ พอให้ซีรัม การทำงานของรีดักเตสลดลง แต่พอเอาซีรัมออก การทำงานของรีดักเตสเพิ่มขึ้นเป็นสิบเท่า. โกลด์สไตน์และบราวน์สงสัย และค้นหาว่าอะไรในซีรัมที่ควบคุมการทำงานของรีดักเตส จนพบว่า ไขมันโปรตีนเบา (low-density lipoprotein คำย่อ LDL) เป็นตัวยับยั้ง (inhibitor) การทำงานของรีดักเตส.
โกลด์สไตน์และบราวน์มีสมมติฐานว่า ผู้ป่วยโรคภาวะไขมันในเลือดสูงทางพันธุกรรม ที่ร่างกายสร้างคอเลสเตอรอลมากเกินไป อาจเพราะมีการกลายพันธุ์ของยีนของรีดักเตส ที่ทำให้มีการสร้างรีดักเตสที่ผิดปกติและไม่ตอบสนองต่อไขมันโปรตีนเบา. ทั้งคู่ทำการทดลอง และพบว่า เซลล์จากผู้ป่วยโรคภาวะไขมันในเลือดสูงทางพันธุกรรม มีการทำงานของรีดักเตสมากกว่าเซลล์ปกติ สี่สิบถึงหกสิบเท่า และไขมันโปรตีนเบาไม่มีผลต่อการทำงานของรีดักเตส. แต่การทดลองต่อมาของทั้งคู่ กลับไม่พบความผิดปกติในตัวเอนไซม์รีดักเตสของผู้ป่วย ซึ่งชี้ว่า สมมติฐานรีดักเตสผิดปกติไม่ถูกต้อง.
ไขมันโปรตีนเบายับยั้งการทำงานของรีดักเตสในเซลล์ปกติ แต่ไม่ทำให้เซลล์ผู้ป่วย. รีดักเตสของเซลล์ผู้ป่วยไม่ได้ผิดปกติ. ดังนั้น น่าจะต้องมีอะไรระหว่างกลาง ที่เป็นปัจจัย. ไขมันโปรตีนเบา จะประกอบไปด้วยโปรตีน ที่เรียกว่าลิโปโปรตีน และไขมัน ซึ่งรวมถึงคอเลสเตอรอล. โกลด์สไตน์และบราวน์ ทดลองป้อนเฉพาะคอเลสเตอรอล โดยไม่มีลิโปโปรตีน และพบว่า คอเลสเตอรอลยับยั้งการทำงานของรีดักเตสอย่างชัดเจน ทั้งในเซลล์ปกติและเซลล์ผู้ป่วย. นั่นคือ รีดักเตสของผู้ป่วยทำงานได้ปกติ ถูกควบคุมด้วยคอเลสเตอรอลได้เหมือนกับรีดักเตสปกติ แต่ถูกควบคุมไม่ได้ถ้าคอเลสเตอรอลอยู่ในรูปไขมันโปรตีนเบา.
ไขมันโปรตีนเบาจับตัวได้ดีกับเซลล์ปกติ แต่ไม่จับกับเซลล์ของผู้ป่วย. เซลล์ปกติมีรีเซปเตอร์สำหรับจับตัวกับไขมันโปรตีนเบา แต่เซลล์ของผู้ป่วยไม่มี. โกลด์สไตน์และบราวน์ ศึกษากลไกนี้ และพบว่า ลิโปโปรตีนของไขมันโปรตีนเบา นำคอเลสเตอรอลไปให้เซลล์ โดยตัวลิโปโปรตีนจะจับตัวกับรีเซปเตอร์ไขมันโปรตีนเบา (LDL receptors) และคอเลสเตอรอลจะถูกแยกออกจากโปรตีนตอนที่เข้าไปอยู่ในเซลล์ ซึ่งคอเลสเตอรอลจะสามารถเข้าควบคุมการทำงานของรีดักเตสได้.
นั่นคือ ในเซลล์ปกติ ไขมันโปรตีนเบา (ซึ่งมีคอเลสเตอรอลอยู่) จับกับรีเซปเตอร์ไขมันโปรตีนเบา และส่งผลยับยั้งการทำงานของรีดักเตส. แต่ในเซลล์ของผู้ป่วยโรคภาวะไขมันในเลือดสูงทางพันธุกรรม ไขมันโปรตีนเบา (ซึ่งมีคอเลสเตอรอลอยู่) ไม่สามารถส่งคอเลสเตอรอลเข้าไปในเซลล์ได้ การทำงานของรีดักเตสไม่ถูกยับยั้ง และส่งผลให้มีการสังเคราะห์คอเลสเตอรอลออกมาอย่างมาก มากกว่าในเซลล์ปกติหกสิบเท่า.
ช่วงเวลาใกล้เคียงกัน อากีระ เอนโด๊ะ (Akira Endo) ที่ขณะนั้นทำงานกับบริษัทยาซันเคียว ในโตเกียว ญี่ปุ่น พยายามค้นหาสารประกอบเพื่อยับยั้งการทำงานของรีดักเตส. เอนโด๊ะมีประสบการณ์จากงานก่อนหน้า ที่เขาค้นพบเอนไซม์จากรา เพื่อย่อยเนื้อผลไม้ที่ปนมาในไวน์และเหล้าผลไม้. เอนโด๊ะรู้เรื่องของราบางชนิด ที่มีโมเลกุลเออโกสเตอรอล (ergosterol) เป็นส่วนประกอบสำคัญของเยื่อหุ้มเซลล์ แทนที่จะเป็นคอเลสเตอรอล เขาเลยคิดว่า ราบางชนิดน่าจะมีสารประกอบที่ยับยั้งกระบวนการสังเคราะห์คอเลสเตอรอลได้.
เอนโด๊ะกับทีมงานค้นหาสารประกอบที่อยากได้ โดยค้นหาจากราประมาณ \(6000\) ชนิด และทดสอบดูว่า น้ำจากราแต่ละชนิด จะยับยั้งการทำงานของรีดักเตสได้หรือไม่ จากการค้นหาอยู่สองปี เอนโด๊ะกับทีมงาน พบสารออกฤทธิ์สกัดจากราสองชนิดที่ยับยั้งการทำงานของรีดักเตสได้ ตัวหนึ่งได้จากรา ไพเธียม อัลติมัม (Pythium ultimum) ซึ่งกลายเป็นยาปฏิชีวนะที่รู้จักกันอยู่แล้ว ชื่อ ซิตรินิน (citrinin). ซิตรินินยับยั้งการทำงานของรีดักเตสได้ แต่เป็นพิษมาก. อีกตัวหนึ่งได้จากรา เพนนิซิเลียม ซิตรินัม (Penicillium citrinum) ซึ่งมาจากสกุลเดียวกับราที่ใช้สกัดยาเพนนิซิลิน.
สำหรับศึกษาและพัฒนาความเป็นยาต่อ เอนโด๊ะกับทีมงานต้องเพาะเลี้ยงเพนนิซิเลียมซิตรินัมมากถึง \(600\) ลิตร เพื่อที่จะสกัดสารประกอบมาได้ปริมาณ \(23\) มิลลิกรัม และพบว่า โมเลกุล ML-236B ซึ่งภายหลังคือ คอมแพคติน (Compactin หรือชื่ออื่น เมวาสแตติน Mevastatin) เป็นสารออกฤทธิ์. เอนโด๊ะกับทีมงานเผยแพร่การค้นพบนี้ และพัฒนาคอมแพคตินต่อเพื่อเป็นยา ซึ่งคือการทดลองในสัตว์. การทดลองในหนู แม้ว่าไม่พบผลเป็นพิษ แต่คอมแพคตินไม่ช่วยลดคอเลสเตอรอลในกระแสเลือดของหนูเลย ไม่ว่าจะให้ยาอยู่เจ็ดวัน หรือใช้ขนาดยาสูงอยู่ถึงห้าสัปดาห์.
ผิดหวัง แต่เอนโด๊ะยังไม่ยอมแพ้. จากการทดลองที่ผ่าน ๆ มา เอนโด๊ะสงสัยว่า ที่คอมแพคตินไม่เป็นผลกับหนู อาจเป็นเพราะ ร่างกายของหนูมีกลไกควบคุมคอเลสเตอรอลที่ต่างไป และเอนโด๊ะจึงเริ่มการทดลองใหม่ในไก่ ซึ่งได้ผลดีมาก และผลในลิงและผลในสุนัข ก็พบการลดลงของคอเลสเตอรอลอย่างเด่นชัด. โอกาสของคอมแพคตินเริ่มสดใส และซันเคียวก็ให้การสนับสนุนอย่างเต็มที่. แต่ นักพิษวิทยาเห็นความผิดปกติในเซลล์ตับของหนูที่ให้คอมแพคตินที่ขนาดยาสูงมาก สุดท้ายหลังจากไตร่ตรองอยู่หลายเดือน ซันเคียวก็ตัดสินใจจะดำเนินการทดสอบทางคลีนิค. แต่แล้ว ซันเคียว ก็สั่งหยุดการพัฒนาคอมแพคตินทันที หลังจาก นักพิษวิทยาของบริษัทสงสัยว่า สุนัขที่ให้คอมแพคตินที่ขนาดยาสูงติดต่อกันสองปี จะมีเนื้องอกในลำไส้.
ในช่วงนั้น บริษัทยาต่าง ๆ รู้เรื่องการพัฒนาคอมแพคตินของซันเคียว. รอย วาเจโลส (Roy Vagelos) หัวหน้าฝ่ายวิจัยของบริษัทเมอร์ค อยากจะเปลี่ยนวิธีการค้นหายา จากเดิมที่การค้นหาสารประกอบทำด้วยการทดลองกับเซลล์หรือจุลชีพ วาเจโลสอยากจะเปลี่ยนเป็นการทดลองกับโมเลกุลเป้าหมาย.
จากงานของโกลด์สไตน์และบราวน์ และการค้นพบคอมแพคตินของเอนโด๊ะ วาเจโลสเห็นโอกาสที่จะได้ลองวิธีใหม่นี้. วาเจโลสและทีมงานที่เมอร์ค ค้นหายาแบบคอมแพคตินจากราชนิดอื่น ๆ และสุดท้าย พบสารประกอบจากรา อัสเพอร์จิลลัส เทอเรียส (Aspergillus terreus) ซึ่งภายหลังคือ โลวาสแตติน (Lovastatin). แต่หลังจากที่เมอร์ครู้ข่าวซันเคียวยกเลิกการพัฒนาคอมแพคติน เมอร์คก็ตัดสินใจยกเลิกการพัฒนาโลวาสแตตินด้วย.
โกลด์สไตน์และบราวน์เองก็รู้เรื่องงานของเอนโด๊ะ. ทั้งคู่สนใจ ติดต่อกับเอนโด๊ะ และได้ตัวอย่างคอมแพคตินมาทดลอง ซึ่งผลการทดลอง นอกจากแสดงในเห็นว่า เมื่อใช้คอมแพคติน การทำงานของรีดักเตสลดลงชัดเจนแล้ว. สิ่งที่โกลด์สไตน์และบราวน์พบใหม่ก็คือ เซลล์สร้างรีดักเตสเพิ่มขึ้น.
ในขณะที่การสังเคราะห์คอเลสเตอรอล ถูกควบคุมด้วยการทำงานของรีดักเตส การสังเคราะห์รีดักเตสเองก็ถูกควบคุมยับยั้งด้วยปริมาณคอเลสเตอรอล. ผลการทดลองที่โกลด์สไตน์และบราวน์พบ แสดงให้เห็นถึง อิทธิพลภาคเสธคู่ (double-negative effect) ในการควบคุมปริมาณคอเลสเตอรอล. นั่นคือ การยับยั้งการทำงานของรีดักเตส ส่งผลให้ไม่มีคอเลสเตอรอลผลิต เมื่อไม่มีคอเลสเตอรอล ก็ไม่มีอะไรยับยั้งการสังเคราะห์รีดักเตส ดังนั้นปริมาณรีดักเตสจึงเพิ่มขึ้น. หมายเหตุ แม้ปริมาณของรีดักเตสเพิ่มขึ้น แต่รีดักเตสไม่ได้ทำงาน.
โกลด์สไตน์และบราวน์ ดีใจมากกับการค้นพบนี้ เพราะว่า งานวิจัยก่อนหน้านี้ทำให้ทั้งคู่รู้ว่า การสังเคราะห์รีดักเตสและรีเซปเตอร์ไขมันโปรตีนเบาถูกควบคุมไปพร้อม ๆ กัน ดังนั้น การเห็นการสังเคราะห์รีดัสเตสเพิ่ม ก็อาจหมายถึงการสังเคราะห์รีเซปเตอร์ไขมันโปรตีนเบาเพิ่มด้วย. การเพิ่มรีเซปเตอร์ไขมันโปรตีนเบา ก็น่าจะทำให้เซลล์สามารถดึงไขมันโปรตีนเบาจากกระแสเลือดเข้าเซลล์ได้มากขึ้น และลดระดับคอเลสเตอรอลในกระแสเลือด ที่เป็นสาเหตุของอาการหัวใจวาย.
นั่นคือ โกลด์สไตน์และบราวน์ วางสมมติฐานว่า สำหรับผู้ป่วยโรคภาวะไขมันในเลือดสูงทางพันธุกรรม รีเซปเตอร์ไขมันโปรตีนเบามีจำนวนน้อย ทำให้คอเลสเตอรอลในกระแสเลือดมีปริมาณมาก. แต่เมื่อใช้คอมแพคตินแล้ว การทำงานของรีดักเตสลด การสังเคราะห์คอเลสเตอรอลในเซลล์ลด การสังเคราะห์รีดักเตสและรีเซปเตอร์ไขมันโปรตีนเบาเพิ่ม รีเซปเตอร์ไขมันโปรตีนเบามีจำนวนเพิ่มขึ้น สามารถรับไขมันโปรตีนเบาจากกระแสเลือดเข้ามาในเซลล์ได้ ช่วยให้ภายในเซลล์มีคอเลสเตอรอลใช้ และทำให้คอเลสเตอรอลในกระแสเลือดมีปริมาณลดลง.
ทั้งคู่ทดสอบสมมติฐาน โดยขอตัวอย่างโลวาสแตตินมาจากเมอร์ค และทดลองกับสุนัข. ผลคือ ทั้งรีเซปเตอร์ไขมันโปรตีนเบามีจำนวนเพิ่มขึ้น และคอเลสเตอรอลในกระแสเลือดมีปริมาณลดลง. ทั้งคู่มั่นใจกับผลการทำงาน แต่จะหายามาให้ผู้ป่วยจากไหน ในเมื่อทั้งซันเคียวและเมอร์คก็ระงับการพัฒนา เนื่องจากกลัวความเสี่ยงของการเกิดเนื้องอกในลำไส้. โกลด์สไตน์และบราวน์ตัดสินใจไปญี่ปุ่นเพื่อปรึกษากับเอนโด๊ะ. ตอนนั้นเอนโด๊ะไม่ได้ทำงานให้ซันเคียวแล้ว เอนโด๊ะย้ายไปทำงานที่มหาวิทยาลัยเกษตรและเทคโนโลยีโตเกียว. เอนโด๊ะ เชื่อว่านักพิษวิทยาอาจจะตีความผลที่เห็นในสุนัขผิด และคิดว่าสิ่งที่นักพิษวิทยาเห็นในลำไส้ อาจจะไม่ใช่เนื้องอก อาจจะเป็นยาที่ไม่ย่อยมากกว่า เพราะว่า การทดลองใช้ขนาดยาที่สูงมาก ซึ่งมากกว่าที่จะใช้ในคนถึงร้อยเท่า.
ค่อนข้างมั่นใจกับยา และด้วยโลวาสแตตินที่ได้มา โกลด์สไตน์และบราวน์ร่วมกับเพื่อนอีกสองคน ทดสอบยากับผู้ป่วยโรคภาวะไขมันในเลือดสูงทางพันธุกรรมจำนวนหกคน และผลที่ได้ คือรีเซปเตอร์ไขมันโปรตีนเบามีจำนวนเพิ่มขึ้น และคอเลสเตอรอลในกระแสเลือดลดลงประมาณ \(27\%\). ผลที่ได้นี้ ช่วยให้เมอร์คตัดสินใจกลับมาพัฒนาโลวาสแตตินต่อ. แต่ผู้บริหารของเมอร์ค ก็ยังกังวลกับความเสี่ยงจากเนื้องอกอยู่. เพื่อทำประเด็นเรื่องเนื้องอกให้ชัดเจน และโอกาสในการใช้ยากับผู้ป่วยภาวะไขมันในเลือดสูงทั่วไป เอ็ดเวิร์ด สโคนิค (Edward Skolnick) หัวหน้าฝ่ายวิจัยพื้นฐานของเมอร์ค ตั้งทีมงานเฉพาะขึ้นมา เพื่อศึกษาผลทางพิษวิทยาให้สมบูรณ์. สโคนิคปรึกษากับโกลด์สไตน์และบราวน์ และโกลด์สไตน์และบราวน์ได้แนะนำวิธีการทดสอบ เพื่อระบุว่า สิ่งที่เห็นในสัตว์ทดลองว่าเป็นผลจากยาจริง ๆ หรือว่าแค่มาจากการทดสอบด้วยขนาดยาสูงมาก ซึ่งสามารถป้องกันได้ง่าย ๆ. ทีมงานนักวิจัยของสโคนิคทดลอง และไม่พบผลร้ายจากยา. สโคนิคโล่งอก และเมอร์คมั่นใจในความปลอดภัยของยา.
ผลจากการทดสอบอยู่สองปี ยืนยันว่า โลวาสแตตินช่วยลดคอเลสเตอรอลในกระแสเลือดได้กว่า \(20\%\) เมอร์คยื่นจดทะเบียนยา และได้เริ่มขายโลวาสแตตินในปี ค.ศ. 1987. ทั้งโลวาสแตติน และคอมแพคติน รวมไปถึงยาที่พัฒนาขึ้นมาภายหลังตัวอื่น ๆ ในกลุ่มนี้ จะเรียกว่า กลุ่มยาสแตติน (Statins). เพื่อการติดตามผลการใช้ยา เมอร์คสนับสนุนการศึกษาห้าปี กับผู้ป่วยระดับคอเลสเตอรอลในกระแสเลือดสูง จำนวน \(4,444\) คน ที่ใช้ยาซิมวาสเตติน (ซึ่งเป็นยาในกลุ่มสแตติน ที่พัฒนาขึ้นมาภายหลัง) และพบว่า ยาช่วยลดอัตราการตายจากหัวใจวายของผู้ป่วยลง \(42\%\). ปัจจุบัน มีีผู้ใช้ยาในกลุ่มสแตตินมากกว่ายี่สิบห้าล้านคนทั่วโลก และอัตราการตายจากหัวใจวายของชาวอเมริกันลดลงเกือบหกสิบเปอร์เซ็นต์ (นับจากที่ อันเซิล คีส์ พบอันตรายจากคอเลสเตอรอล).
อุตสาหกรรมยา การค้นหาและพัฒนายา. โรนัล คริสโตเฟอร์ (Ronald Christopher) จากบริษัทยาอารีนา บรรยายเรื่อง การเลือกสารประกอบและการศึกษาก่อนคลีนิก ว่า การค้นหายาเป็นกิจกรรมที่อัตราการล้มเหลวสูงมาก ประมาณหนึ่งในพัน นั่นคือ จากขั้นตอนแรก ๆ อาจมีสารประกอบที่สนใจอยู่ประมาณห้าพันถึงหนึ่งหมื่นตัว สุดท้ายจะเหลือแค่ประมาณสิบตัวที่ผ่านกระบวนการไปจนถึงการทดสอบทางคลีนิกกับมนุษย์ได้. ระยะเวลาในการค้นหายา โดยเฉลี่ย จะประมาณสิบสองปี และค่าใช้จ่ายในการพัฒนายาแต่ละตัว ประมาณ \(1.3\) พันล้านดอลล่าร์ หรือประมาณสี่แสนล้านบาท ต่อการค้นหาและพัฒนายาที่จะได้รับการขึ้นทะเบียนหนึ่งตัว. (หมายเหตุ คณะของดิมาสี ประมาณตัวเลขอยู่ที่ \(2.87\) พันล้านดอลล่าร์ แต่ประสาตและมายลานคอดิ ประมาณค่าใช้จ่ายอยู่ที่ \(648\) ล้านดอลล่าร์ซึ่งต่ำกว่ามาก. อย่างไรก็ตาม แมทธิว เฮอร์เปอร์ ได้เขียนบทความ “The Cost Of Developing Drugs Is Insane. That Paper That Says Otherwise Is Insanely Bad” Oct 16, 2017,10:58am EST ในเวปไซต์ http://www.forbes.com ซึ่งวิจารณ์วิธีประเมินของประสาตและมายลานคอดิ โดยเฉพาะเรื่องที่ประสาตและมายลานคอดิ ไม่ได้รวมค่าใช้จ่ายของความล้มเหลวในกระบวนการค้นหายาเข้าไปด้วย. เฮอร์เปอร์วิจารณ์ว่า ผลสรุปของประสาตและมายลานคอดิเป็นลักษณะของความลำเอียงไปทางคนที่รอด survivorship bias. ความลำเอียงไปทางคนที่รอด หมายถึง การวิเคราะห์ที่ใช้ผลสรุปแทนภาพรวมทั้งหมด แต่ใช้ข้อมูลเฉพาะจากกลุ่มข้อมูลที่ทำได้ดีหรือกลุ่มผู้รอด. ไม่ว่าจะอย่างไร กิจกรรมการค้นหาพัฒนายาเป็นกิจกรรมที่ลงทุนมหาศาล อาศัยเครื่องมือขั้นสูงและทักษะกับความทุ่มเทอย่างยิ่งยวดของบุคคลากรที่เกี่ยวข้อง.)
โรนัล คริสโตเฟอร์ อธิบายการเลือกสารประกอบมาเป็นยาว่า มีเกณฑ์ในการพิจารณาอย่าง ๆ หลาย เช่น คุณสมบัติทางเภสัชวิทยา ได้แก่ การออกฤทธิ์ที่ดี สมรรถนะการเลือกที่สูง (สารประกอบจับตัวกับเป้าหมายดีกว่าจับตัวกับชีวะโมเลกุลอื่นในร่างกาย มากกว่าพันเท่า) ประสิทธิผลที่ดีในการทดลองกับสัตว์ (แสดงให้เห็นว่ามันได้ผล). นอกจากนั้น ก็ยังพิจารณาเรื่อง เมแทบอลิซึมของยา และคุณสมบัติทางเภสัชจลนศาสตร์ (ร่ายกายตอบสนองต่อยาอย่างไร) รวมถึง การปฏิสัมพันธ์ระหว่างยากับยา (drug–drug interactions) ว่ายาตัวใหม่นี้จะไม่ไปกวนยาอื่นที่ผู้ป่วยใช้อยู่ และปัจจัยด้านความปลอดภัย เช่น ผลการศึกษาด้านความปลอดภัยในทางที่ดีทั้งการศึกษาในหลอดทดลอง และในสัตว์ทดลอง.
คริสโตเฟอร์ยกตัวอย่างประสบการณ์การพัฒนายาอโลกลิบติน สำหรับบำบัดโรคเบาหวาน. โรคเบาหวาน เป็นภาวะที่ร่างกายมีน้ำตาลในเลือดสูง. ระดับน้ำตาลในเลือด (blood glucose) ถูกควบคุมด้วยอินซูลิน (insulin). การปล่อยอินซูลินถูกควบคุมด้วยฮอร์โมนอินคริตินส์ (incretins) การควบคุมอินคริตินส์ถูกควบคุมด้วยดีพีพีสี่ (Dipeptidyl peptidase-4 คำย่อ DPP-4). การควบคุมในร่ายกายมีอยู่สองแบบหลัก ๆ ได้แก่ การควบคุมเชิงบวก คือการสนับสนุนหรือกระตุ้น และควบคุมเชิงลบ คือการลดหรือยับยั้ง. อินซูลินควบคุมระดับน้ำตาลในเลือดในเชิงลบ อินคริตินส์ควบคุมอินซูลินในเชิงบวก ดีพีพีสี่ควบคุมอินคริตินส์ในเชิงลบ. นั่นคือ หากอินซูลินเพิ่มขึ้น ระดับน้ำตาลในเลือดจะลดลง. หากอินคริตินส์เพิ่มขึ้น อินซูลินจะเพิ่มขึ้น. แต่หากดีพีพีสี่ทำงาน อินคริตินส์จะลดลง ส่งผลให้อินซูลินลดลง ส่งผลให้ระดับน้ำตาลในเลือดเพิ่มขึ้น. ยาบางตัว เช่น เอ็กซีนาไทด์ (Exenatide) เลือกเป้าหมายเป็นรีเซปเตอร์ของอินคริตินส์. ตัวยาจะไปจับกับรีเซปเตอร์ของอินคริตินส์ เพื่อส่งผลเหมือนการเพิ่มของอินคริตินส์. เอ็กซีนาไทด์ เป็นยาฉีดและมีผลข้างเคียงค่อนข้างมาก. ทีมงานของคริสโตเฟอร์ เลือกเป้าหมายเป็นดีพีพีสี่ และต้องการหาโมเลกุลที่ยับยั้งดีพีพีสี่ (DPP4 inhibitor). การยับยั้งดีพีพีสี่ เท่ากับเพิ่มการทำงานของอินคริตินส์ อินคริตินส์ทำงานมากขึ้นจะไปเพิ่มอินซูลิน อินซูลินเพิ่มขึ้นจะไปลดระดับน้ำตาลในเลือด.
ตอนนั้น มียาที่ยับยั้งดีพีพีสี่ในตลาดอยู่หลายตัวแล้ว เช่น วิลดากลิปทิน. ทีมงานของคริสโตเฟอร์ ศึกษาโครงสร้างทางเคมีของดีพีพีสี่ ซึ่งเป็นงานที่มีขั้นตอนที่ซับซ้อนมาก ตั้งแต่การโคลนดีพีพีสี่ และทำกระบวนการต่าง ๆ ที่จะทำให้ดีพีพีสี่ตกผลึก และถ่ายภาพดีพีพีสี่ที่ตกผลึกด้วยเอ็กซ์เรย์ ซึ่งต้องใช้เครื่องซินโครตรอน. ภาพถ่ายที่ได้จะเป็นภาพของรูปแบบการกระเจิงของเอ็กซ์เรย์ ซึ่งต้องใช้นักชีววิทยาโครงสร้างอ่าน ตีความ และแปลงออกมาเป็นแบบจำลองคอมพิวเตอร์ของโครงสร้างเคมีสามมิติ ที่นักเคมีสามารถใช้วิเคราะห์ได้ต่อไป. นักเคมีในทีมงานของคริสโตเฟอร์ ดูโครงสร้างดีพีพีสี่ และการเข้าอู่จับตัวกับวิลดากลิปทิน แล้วพบว่า ในการจับตัวกันของวิลดากลิปทินและดีพีพีสี่ มีการจับด้วยพันธะโควาเลนท์อยู่. พันธะโควาเลนท์ทำให้โมเลกุลยาจับตัวกับดีพีพีสี่แน่น. การจับดีพีพีสี่แน่นเกินไป อาจก่อให้เกิดผลข้างเคียงต่อระบบภูมิคุ้มกัน. ทีมงานของคริสโตเฟอร์ ต้องการจะพัฒนายาใหม่ที่จับดีพีพีสี่ โดยไม่มีพันธะโควาเลนท์.
การค้นหาออกแบบและพัฒนายาของทีมของคริสโตเฟอร์ ทำโดยอาศัยโครงสร้างโมเลกุล. ในการค้นยาออกแบบยา โดยทั่วไป จะมีสองแนวทางหลัก ๆ คือ อาศัยลิแกนต์ (ligand-based) หรืออาศัยโครงสร้าง (structure-based). วิธีอาศัยลิแกนต์ ไม่จำเป็นต้องรู้โครงสร้างทางเคมีสามมิติของเป้าหมาย แต่ต้องรู้จักบางลิแกนต์ของเป้าหมาย แล้วสร้างแบบจำลองทำนายการจับตัว และค้นหาโมเลกุลที่อาจเป็นยาได้จากแบบจำลองทำนาย (ที่สร้างโดยอาศัยข้อมูลลิแกนต์เหล่านั้น). วิธีอาศัยโครงสร้าง ต้องรู้โครงสร้างของโมเลกุลเป้าหมาย. ยา มักเป็นโมเลกุลขนาดเล็ก แต่เป้าหมาย เช่น โปรตีน เป็นโมเลกุลขนาดใหญ่. การหาโครงสร้างสามมิติของโมเลกุลขนาดใหญ่เป็นเรื่องซับซ้อนและใช้ทักษะสูง แต่หากได้โครงสร้างสามมิติของโมเลกุลเป้าหมายมาแล้ว นักเคมีจะดูโครงสร้างของตำแหน่งจับตัวในโปรตีนเป้าหมาย แล้วจึงพิจารณาหาลิแกนต์ โดยอาจเริ่มจากส่วนเล็ก ๆ ของโครงสร้างทางเคมีที่ต้องการ แล้วค่อยค้นหาโมเลกุลของลิแกนต์ตามนั้น หรืออาจจะค้นหาจากสารประกอบที่มีอยู่ในฐานข้อมูล ด้วยวิธีการกลั่นกรองเสมือน หรืออาจจะออกแบบโครงสร้างของลิแกนต์ขึ้นมาใหม่เลยก็ได้.
วิธีการกลั่นกรองเสมือน (virtual screening คำย่อ vs) เป็นการใช้คอมพิวเตอร์เข้ามาช่วยค้นหาโมเลกุลต่าง ๆ จากฐานข้อมูล เพื่อหาโมเลกุลที่มีโอกาสสูงในการนำมาพัฒนาต่อเป็นยา. โมเลกุลต่าง ๆ ที่อาจเป็นยาได้ มีจำนวนมหาศาล. การทดสอบแต่ละโมเลกุลกับเป้าหมายในหลอดทดลองมีค่าใช้จ่ายสูง. การใช้คอมพิวเตอร์ช่วยกลั่นกรองเลือกโมเลกุลต่าง ๆ ก่อน แล้วค่อยเลือกทดสอบโมเลกุลที่ผ่านการกลั่นกรองขั้นต้นกับเป้าหมายในหลอดทดลอง จะช่วยลดค่าใช้จ่าย เวลา และทรัพยากรบุคคลในการพัฒนายาลงได้มาก. ในทางปฏิบัติ วิธีการกลั่นกรองเสมือนก็ไม่ได้ค้นหากับทุกโมเลกุลที่เป็นไปได้ แต่อาจจะเลือกจากฐานข้อมูลของยาที่ได้มีการทดสอบแล้ว อาจเลือกจากรายการของสารประกอบที่มีอยู่ในคลังของบริษัทแล้ว อาจเลือกจากฐานข้อมูลจากผู้ขาย เป็นต้น โดยอาจลำดับความสำคัญของการค้นหา จากยาที่มีการทดสอบแล้ว ต่อด้วยสารต่าง ๆ ที่มีอยู่คลัง แล้วไปสารต่าง ๆ ที่สามารถจัดซื้อได้ จนสุดท้ายถึงค้นหาสารต่าง ๆ ที่จะต้องสังเคราะห์ขึ้นใหม่. หากพบโมเลกุลจากฐานข้อมูลยาที่มีการทดสอบแล้ว จะช่วยลดค่าใช้จ่ายในการศึกษาหลาย ๆ อย่างที่มีผลการศึกษาอยู่แล้ว. สารที่มีอยู่แล้วในคลังก็จัดหาได้ง่ายกว่า และสารที่สามารถหาซื้อได้ ก็สะดวกและมักเสียค่าใช้จ่ายน้อยกว่าการสังเคราะห์สารขึ้นมาเองใหม่.
วิธีการกลั่นกรองเสมือน อาจใช้การทำนายการเข้าอู่ (docking) ซึ่ง จะทำนายรูปร่างและทิศทางการวางตัวของโมเลกุล เมื่อโมเลกุลจับตัวกับเป้าหมาย ซึ่งผลการทำนายนี้อาจใช้ประกอบ เพื่อทำนายอัตราการจับตัวกัน (binding affinity). อัตราการจับตัวกัน เป็นโอกาสของการจับตัวกันระหว่างลิแกนต์กับเป้าหมาย. แบบจำลองที่ทำนายอัตราการจับตัวกัน จะเรียกว่า ฟังก์ชันคะแนน (scoring function). ฟังก์ชันคะแนน อาจทำนายโอกาสของการจับตัว ด้วยพลังงานรวมของการจับตัวกัน โดยคำนวณจากทฤษฎีสนามแรง ซึ่งอาศัยรูปร่างและทิศทางการวางตัวของโมเลกุลที่จับตัวกัน. ค่าพลังงานที่ต่ำกว่า หมายถึงผลการจับตัวที่มีเสถียรภาพมากกว่า และโอกาสที่มากว่าของการจับตัวกัน. การใช้แบบจำลองการเรียนรู้ของเครื่องเป็นอีกแนวทางหนึ่งที่สามารถนำมาใช้สร้างฟังก์ชันคะแนนได้. หมายเหตุ ตัวอย่างในแบบฝึกหัด 1.1.0.2.2 เป็นแค่การทำนายการจับตัวกัน ไม่ได้มีการประเมินโอกาสจับตัวกันออกมาเป็นตัวเลข ซึ่งฐานข้อมูลดียูดีไม่มีข้อมูลนี้อยู่. แต่หากมีข้อมูลอัตราการจับตัวกัน ซึ่งมักวัดเป็นเปอร์เซ็นต์การจับตัวต่อความเข้มข้นของสารละลายของลิแกนต์ (%binding per molar concentration) ก็สามารถนำมาสร้างเป็นแบบจำลองได้ โดยการทำนายลักษณะนี้เป็นการทำนายค่าต่อเนื่อง และเหมาะที่จะวางกรอบเป็นแบบจำลองการหาค่าถดถอย.
การค้นหาและพัฒนายา มักดำเนินการในลักษณะการวนทวนกลั่นกรอง นั่นคือ เป็นลักษณะวนค้นหา ปรับปรุง และสลับกันไป จนกว่าจะได้ลิแกนต์ที่มีลักษณะความเป็นยาสูงออกมา.
หลังจากได้ลิแกนต์ที่ผ่านรอบแรกมา ทีีมพัฒนาจะปรับปรุงโมเลกุล โดยอาจจะค้นหาโมเลกุลอื่น ๆ ที่ใกล้เคียงกับลิแกนต์เหล่านั้น หรืออาจจะปรับโครงสร้างบางส่วนของลิแกนต์เหล่านั้น เพื่อให้มีคุณสมบัติทางยาต่าง ๆ ดีขึ้น. คุณสมบัติทางยาต่าง ๆ ที่ปรับปรุง ได้แก่ อัตราการจับตัวกับเป้าหมาย (\(IC_{50} \leq 100\) นาโนโมลาร์ ซึ่งค่า \(IC_{50}\) วัดจากความเข้มข้นของลิแกนต์ที่สามารถจับกับเป้าหมายได้ครึ่งหนึ่ง), สมรรถนะการเลือก (ลิแกนต์มีการจับตัวกับเป้าหมายได้ดีกว่าจับตัวกับโมเลกุลอื่นที่คล้ายเป้าหมายหนึ่งพันเท่า), รวมถึงการออกฤทธิ์ของยา คุณสมบัติเมแทบอลิซึมของยา คุณสมบัติทางเภสัชจลนศาสตร์และเภสัชพลศาสตร์ เป็นต้น. ในขั้นตอนการพัฒนายา อาจมีการใช้แบบจำลองทำนาย เช่น ความสัมพันธ์เชิงปริมาณระหว่างโครงสร้างและกิจกรรม (Quantitative Structure-Activity Relationship คำย่อ QSAR) เข้ามาช่วย. ความสัมพันธ์เชิงปริมาณระหว่างโครงสร้างและกิจกรรม เป็นการทำนายกิจกรรมหรือคุณสมบัติของโมเลกุล จากโครงสร้างของโมเลกุล ซึ่งกิจกรรมที่ทำนาย อาจเป็น ผลกับเป้าหมายหลังการจับตัว (ว่าเป็น ผลทำการ agonism ที่ทำให้เป้าหมายทำงานมากขึ้น หรือผลต่อต้าน antagonism ที่ลดการทำงานของเป้าหมายลง), ชีวปริมาณออกฤทธิ์ (bioavailability), การละลายน้ำ (solubility), สมรรถนะการเลือก, การออกฤทธิ์ เป็นต้น. ความสัมพันธ์เชิงปริมาณระหว่างโครงสร้างและกิจกรรม อาจสร้างจากพื้นฐานทางฟิสิกส์และเคมี หรืออาจจะสร้างตามแนวทางการเรียนรู้ของเครื่องโดยอาศัยข้อมูลก็ได้ โดย คล้ายกับแบบฝึกหัด 1.1.0.2.2 โครงสร้างทางเคมีจะถูกแปลงเป็นลักษณะสำคัญเชิงเลข ที่อาจเรียกว่า ตัวบอก (descriptor) เพื่อให้สามารถใช้คำนวณในแบบจำลองได้.
หลังจากทีมงานของคริสโตเฟอร์ทำงานอย่างหนัก กระบวนการค้นหาออกแบบและพัฒนาโมเลกุลเสร็จสิ้น ทีมงานได้อโลกลิบติน (Aloglibtin). อโลกลิบตินเข้าอู่จับตัวกับดีพีพีสี่ได้ และไม่มีพันธะที่เป็นพันธะโควาเลนท์. อโลกลิบตินจับตัวกับดีพีพีสี่สักพักแล้วก็หลุด และกลับไปจับตัวใหม่ สลับกันไป เปิดโอกาสให้ดีพีพีสี่เป็นอิสระเป็นพัก ๆ ลดความเสี่ยงของผลข้างเคียงต่อระบบภูมิคุ้มกัน.
ทีมงานทดสอบอโลกลิบตินในหลอดทดลอง และพบว่าอโลกลิบตินมีการออกฤทธิ์ที่ดี (\(IC_{50} = 6.9\) ซึ่ง \(IC_{50}\) สำหรับการออกฤทธิ์ของตัวยับยั้ง วัดจากความเข้มข้นของสารละลายยา ที่เพียงพอที่จะยับยั้งการทำงานของเป้าหมายได้ \(50\%\). ดังนั้นตัวเลขน้อยกว่า หมายถึงการออกฤทธิ์ที่ดีกว่า). ยาตัวอื่นในกลุ่มเดียวกันที่อยู่ในตลาด มีการออกฤทธิ์วัดด้วย \(IC_{50}\) เป็น \(23.8\) และ \(12.1\) ซึ่งทั้งหมดจัดว่ามีการออกฤทธิ์ที่ดี.
ผลการทดสอบสมรรถนะการเลือกของอโลกลิบตินก็ออกมาดี. อโลกลิบติน มีอัตราการจับตัวกับดีพีพีสี่ ดีกว่าการจับตัวกับโปรตีนที่ใกล้เคียงมากกว่าหนึ่งแสนเท่า สำหรับโปรตีนที่ใกล้เคียงแต่ละตัว ซึ่งได้แก่ DPP-2, DPP-8, DPP-9, FAP, PREP, และ Tryptase.
การทดสอบกับสัตว์ทดลอง แสดงผลที่ดีเช่นกัน. ผลในลิง แสดง (1) ความเข้มข้นของยาในกระแสเลือดหลังจากรับยาเข้าไป โดยความเข้มข้นเพิ่มจนไปถึงจุดสูงสุด ใช้เวลาประมาณหนึ่งชั่วโมง หลังจากนั้นค่อย ๆ ลดลง และความเข้มข้นของยาในกระแสเลือดเป็นไปตามขนาดยาที่ได้ ซึ่งนี่เป็นการดูการตอบสนองของร่างกายต่อยา ซึ่งผลเป็นไปตามที่ทีมงานคาด และ (2) เปอร์เซ็นต์การยับยั้งการทำงานของดีพีพีสี่ หลังรับยาเข้าไป ซึ่งเปอร์เซ็นต์ยับยั้งสูงสุดอยู่ที่ประมาณ \(90\)% หลังจากรับยาไปราว ๆ สองถึงสามชั่วโมง แต่โดยรวมเปอร์เซ็นต์ยับยั้งค่อนข้างคงที่ต่อเวลาในรอบยี่สิบสี่ชั่วโมง และยังค่อนข้างคงที่ต่อขนาดยาที่ทดสอบด้วย (2mg/kg, 10mg/kg, และ 30 mg/kg) ซึ่งทีมงานก็พอใจ.
ผลทดสอบกับหนูทดลอง ที่มีกลุ่มควบคุม (ไม่เป็นโรค) และกลุ่มที่หนูเป็นโรคเบาหวาน (Neonatally streptozotocin-induced diabetic rats คำย่อ N-STZ-1.5 rats) ก็ได้ผลที่ดี. ผลกับการทำงานของดีพีพีสี่ แสดงการลดลงของเปอร์เซ็นต์การทำงานของดีพีพีสี่ตามขนาดยาที่ใช้. ผลกับปริมาณของอินคริตินส์ แสดงการเพิ่มขึ้นของระดับอินคริตินส์ตามขนาดยาที่ใช้. ผลกับอินซูลินในกระแสเลือดต่อเวลา แสดงการเพิ่มขึ้นของอินซูลินต่อเวลา ตามขนาดยาที่ใช้. ผลกับกลูโคสในกระแสเลือดต่อเวลา แสดงการลดลงของกลูโคสต่อเวลา ตามขนาดยาที่ใช้.
นอกจากการทดสอบการลดระดับน้ำตาลในเลือดแล้ว สำหรับโรคเบาหวาน ยังต้องทดสอบด้วยว่ายาจะไม่ทำให้เกิดอาการน้ำตาลต่ำ (hypoglycemia). นั่นคือ ต้องทดสอบว่า ยาจะไม่ไปลดน้ำตาลในเลือดมากเกินไป. จากการทดลองกับหนูที่อดอาหาร และกินอโลกลิบตินเข้าไปที่ขนาดยาสูง (30mg/kg และ 100mg/kg) เปรียบเทียบกับกลุ่มควบคุม และเปรียบเทียบกับกลุ่มที่กินนาทิไกลไนด์ ยาซึ่งทีมงานรู้ว่าให้ผลด้านนี้ไม่ดี ทีมงานไม่พบว่า อโลกลิบตินทำให้ระดับน้ำตาลลดต่ำเกินไปหรือระดับอินซูลินสูงเกินไป.
การทดลองต่าง ๆ ข้างต้นเป็นการให้ยาครั้งเดียว การศึกษาสภาพทนทาน (robustness) ของยา จะทดสอบโดยให้ยาติดต่อกันเป็นเวลานาน ซึ่งผลที่ได้ แสดงการลดลงของการทำงานของดีพีพีสี่ตามขนาดยา การเพิ่มขึ้นของอินคริตินส์ตามขนาดยา เมื่อใช้ยาติดต่อกัน สำหรับหนูทดลองหลาย ๆ ชนิด. ผลสภาพทนทานเป็นไปด้วยดี.
การศึกษาเมแทบอลิซึมของยา พบว่ายาถูกย่อยสลายด้วยเอนไซม์ CYP-2D6 และ CYP-3A4 และยามีผลกระทบต่อการยับยั้งหรือกระตุ้นเอนไซม์ทั้งสองน้อยมาก. นอกจากนั้น ผลศึกษาแสดงการจับของยากับโปรตีนในน้ำเลือดต่ำมาก และไม่พบปฏิสัมพันธ์กับยาตัวอื่น เมื่อทดสอบกับยาเบาหวานตัวอื่น ๆ. ทีมงานโล่งใจกับผลทดสอบนี้.
การทดสอบเพื่อวัดข้อมูลเภสัชจลนศาสตร์ แสดงชีวปริมาณออกฤทธิ์ที่น่าพอใจ (F เป็น 87% ในลิงที่ให้อโลกลิบตินขนาด 10mg/kg หนึ่งครั้ง ซึ่ง F เป็นสัดส่วนของยาที่ดูดซึมเข้าไปในกระแสเลือดต่อยาที่กินเข้าไป). ค่าครึ่งอายุที่ 5.7 ชั่งโมง (ในลิง และค่าครึ่งอายุ เป็นดัชนีที่บอกเวลาที่ยาลดความเข้มข้นเหลือครึ่งหนึ่งจากความเข้มข้นสูงสุด) ซึ่งคริสโตเฟอร์รู้สึกว่าน้อยไปนิดและอยากได้ที่แปดชั่วโมง เพื่อที่ผู้ป่วยจะสามารถกินยาครั้งเดียวต่อวันได้ แต่ก็หวังว่าค่าครึ่งอายุในมนุษย์จะมากขึ้นกว่านี้. เส้นทางการขับถ่ายยาออกจากร่างกายคือผ่านปัสสาวะและอุจจาระ.
การทดลองด้านความปลอดภัยของยา ซึ่งทีมงานของคริสโตเฟอร์ต้องทำการศึกษามากกว่ายี่สิบการทดสอบ และใช้งบประมาณไปหลักสิบล้านดอลล่าร์ ผลที่ได้สรุปว่า ไม่พบความเป็นพิษต่อระบบประสาทกลาง ไม่พบความเป็นพิษต่อหัวใจและหลอดเลือด ไม่พบความเป็นพิษกับระบบปอดและทางเดินหายใจ ไม่พบความพิษทางพันธุกรรม ไม่พบความเป็นพิษเมื่อใช้ต่อเนื่อง (กับยาขนาด 200mg/kg ในสุนัข โดยให้ติดต่อกันทุกวันเป็นเวลา 9 เดือน) ซึ่งจากผลที่ได้ทีมงานสามารถนำไปคำนวณความปลอดภัยในมนุษย์ ซึ่งผลที่ได้ถือว่าปลอดภัยมาก.
หลังจากได้ผลที่น่าพอใจกับสัตว์ทดลองแล้ว ยาจึงจะมีโอกาสได้ทดสอบทางคลีนิกกับมนุษย์ได้ต่อไป ก่อนที่จะได้รับการพิจารณาเพื่อการรับรองขึ้นทะเบียนยา.
“Whatever you do may seem insignificant to you,
but it is most important that you do it.”—Mohandas Karamchand Gandhi
“อะไรก็ตามที่เราทำ มันอาจดูเล็กน้อยไม่สำคัญ
แต่มันสำคัญที่เราทำมัน.”—มหาตมา คานธี
3.1.0.3.1 แบบฝึกหัด
จากเรื่องการหยุดก่อนกำหนด ในหัวข้อ [sec: ann applications] จงเขียนโปรแกรม เพื่อสร้างข้อมูล และฝึกโครงข่ายประสาทเทียมสองชั้น ขนาด \(100\) หน่วยย่อย และทดลอง และเปรียบเทียบผลการทดลอง กับผลที่แสดงในรูป [fig: early stopping motivation]. สำหรับข้อมูล ให้สร้างจากความสัมพันธ์ \(y = x + 0.3 \sin (2 \pi x) + 0.3 \epsilon\) เมื่อ \(\epsilon \sim \mathcal{U}(0,1)\). สร้าง \(40\) จุดข้อมูลสำหรับการฝึก และ \(20\) จุดข้อมูลสำหรับการทดสอบ. หลังจากนั้น ให้เพิ่มเงื่อนไขการหยุดก่อนกำหนด พร้อมแบ่งข้อมูลส่วนหนึ่งออกมาจากข้อมูลฝึก มาเป็นข้อมูลตรวจสอบ ทดลองฝึกแบบจำลอง ที่มีการหยุดก่อนกำหนด เปรียบเทียบผล สรุป และอภิปราย.
หมายเหตุ ตัวอย่างในรูป [fig: early stopping motivation] ใช้การกำหนดค่าน้ำหนักเริ่มต้น ที่ดัดแปลงมาจากวิธีเหงี่ยนวิดโดรว์ เพื่อให้เห็นภาพชัดเจนขึ้น และลดเวลาในการฝึก. การใช้การกำหนดค่าน้ำหนักเริ่มต้นจากการสุ่มค่า อาจต้องทำการฝึกนานกว่าจำนวนสมัยฝึกที่เห็นในรูป [fig: early stopping motivation].
3.1.0.3.2 แบบฝึกหัด
จากเรื่องเส้นโค้งเรียนรู้ ในหัวข้อ [sec: learning curve] จงเขียนโปรแกรม เพื่อทดลองสร้างเส้นโค้งเรียนรู้. จงสร้างข้อมูลขึ้นมา \(40\) จุดสำหรับฝึก และ \(25\) จุดสำหรับทดสอบ จากความสัมพันธ์ \(y = x + 8 \sin(x) + \epsilon\) เมื่อ \(x \in [0, 4\pi]\) และ \(\epsilon \sim \mathcal{N}(0,1)\). แล้ว สร้างเส้นโค้งเรียนรู้สำหรับ (ก) โครงข่ายประสาทเทียมสองชั้น ที่มี \(2\) หน่วยซ่อน, (ข) โครงข่ายประสาทเทียมสองชั้น ที่มี \(8\) หน่วยซ่อน และ (ค) โครงข่ายประสาทเทียมสองชั้น ที่มี \(64\) หน่วยซ่อน โดยดำเนินการฝึกและทดสอบแบบจำลอง \(5\) ครั้ง ครั้งแรกใช้ข้อมูลฝึก \(8\) จุด ต่อมาใช้ \(16\), \(24\), \(32\), และ \(40\) จุดตามลำดับ. วัดค่ารากที่สองของค่าเฉลี่ยค่าผิดพลาดกำลังสองของทั้งข้อมูลทดสอบ และข้อมูลฝึก. นำเสนอ (ดูตัวอย่างรูป [fig: learning-curve tests] และ [fig: real learning curves]) อภิปรายผลที่ได้ และสรุป.
หมายเหตุ ให้ฝึกโครงข่ายประสาทเทียมให้สมบูรณ์ดีทุกครั้ง อาจใช้วิธีเหงี่ยนวิดโดรว์ ช่วยในการกำหนดค่าน้ำหนักเริ่มต้น เพื่อช่วยลดเวลาในการฝึกลงได้.
3.1.0.3.3 แบบฝึกหัด
จากวิธีคำนวณค่าเกรเดียนต์เชิงเลข ด้วย \[\begin{eqnarray} \nabla_{\theta} E(\boldsymbol{\theta}) = \begin{bmatrix} \frac{\partial E}{\partial \theta_1} \\ \frac{\partial E}{\partial \theta_2} \\ \vdots \\ \frac{\partial E}{\partial \theta_M} \\ \end{bmatrix} \mbox{ และ } \frac{\partial E}{\partial \theta_i} \approx \frac{E(\begin{bmatrix} \vdots \\ \theta_{i-1} \\ \theta_i + \epsilon \\ \theta_{i+1} \\ \vdots \\ \end{bmatrix}) - E(\begin{bmatrix} \vdots \\ \theta_{i-1} \\ \theta_i \\ \theta_{i+1} \\ \vdots \\ \end{bmatrix})}{\epsilon} \label{eq: one-sided numerical grad} \end{eqnarray}\] เมื่อ \(E(\boldsymbol{\theta})\) คือค่าฟังก์ชันจุดประสงค์ และ \(\boldsymbol{\theta} = \{\theta_1, \ldots, \theta_M \}\) คือพารามิเตอร์ของแบบจำลอง ที่มีจำนวนพารามิเตอร์ทั้งหมด \(M\) ตัว.
จงตรวจสอบค่าเกรเดียนต์ที่คำนวณจากวิธีแพร่กระจายย้อนกลับ เปรียบเทียบกับค่าเกรเดียนต์ที่คำนวณจากวิธีการเชิงเลข โดยให้ใช้ค่า \(\epsilon\) เป็น \(1\), \(0.01\) และ \(0.0001\) ตามลำดับ. จงสรุปและอภิปรายผล.
รายการ [code: nGrad] แสดงตัวอย่างโปรแกรมคำนวณเกรเดียนต์เชิงเลยแบบทางเดียว (one-sided numerical gradient calculation) ตามสมการ \(\eqref{eq: one-sided numerical grad}\). ตัวอย่างการใช้งาน คือ
dE = nGrad_oneside(cross_entropy, x, y, net, epsilon=1e-4)เมื่อ cross_entropy คือฟังก์ชันจุดประสงค์. ตัวแปร x และ y เป็นข้อมูล. ตัวแปร net เป็นแบบจำลองของโครงข่ายประสาทเทียม นิยามดังที่ได้อภิปราย. ผลลัพธ์ dE เป็นไพธอนดิกชันนารี ที่เก็บค่าเกรเดียนต์ของค่าน้ำหนักและไบอัส ที่เรียกได้ เช่น dE['weight1'] และ dE['bias1'] คือ เกรเดียนต์ของค่าน้ำหนักและไบอัสของชั้นคำนวณที่หนึ่ง.
def nGrad_oneside(lossf, datX, datY, net, epsilon=1e-4):
num_layers = net['layers']
ngrad = {'layers': num_layers}
yc = mlp(net, datX)
lossc = lossf(yc, datY)
for i in range(1, num_layers):
# weight
w = net['weight%d'%i]
gradw = np.zeros(w.shape)
nr, nc = gradw.shape
for r in range(nr):
for c in range(nc):
wu = w.copy()
wu[r, c] += epsilon
net_ = net.copy()
net_['weight%d'%i] = wu
yu = mlp(net_, datX)
lossu = lossf(yu, datY)
gradw[r,c] = (lossu - lossc)
ngrad['weight%d'%i] = gradw/epsilon
# bias
b = net['bias%d'%i]
gradb = np.zeros(b.shape)
nr, _ = gradb.shape
for r in range(nr):
bu = b.copy()
bu[r] += epsilon
net_ = net.copy()
net_['bias%d'%i] = bu
yu = mlp(net_, datX)
lossu = lossf(yu, datY)
gradb[r,0] = (lossu - lossc)
ngrad['bias%d'%i] = gradb/epsilon
return ngrad