2 พื้นฐาน
“Divide each difficulty into as many parts as is feasible and necessary to resolve it.”
—René Descartes
“แตกปัญหาออกเป็นส่วนย่อย ๆ เท่าที่จะทำได้และจำเป็นที่จะแก้มันได้”
—เรอเน เดการ์ต
ศาสตร์การรู้จำรูปแบบและการเรียนรู้ของเครื่อง อาศัยพื้นฐานจากหลาย ๆ ศาสตร์ การทำความเข้าใจศาสตร์นี้ และพัฒนาการ จำเป็นต้องอาศัยศาสตร์พื้นฐาน. บทนี้จะทบทวนศาสตร์พื้นฐานที่สำคัญ คือ พีชคณิตเชิงเส้น ความน่าจะเป็น และการหาค่าดีที่สุด.
2.1 พีชคณีตเชิงเส้น
การรู้จำรูปแบบและการเรียนรู้ของเครื่อง เกี่ยวข้องกับข้อมูลและตัวแปรจำนวนมาก. พีชคณีตเชิงเส้น 1 มีเครื่องมือและทฤษฎีต่าง ๆ ที่ช่วยอำนวยความสะดวก ในทำงานกับตัวแปรจำนวนมาก ดังนั้น จึงเป็นเป็นพื้นฐานที่สำคัญ
สเกล่าร์ (scalar) หมายถึง ตัวเลขเดี่ยว เช่น ตัวเลข \(3\) ตัวเลข \(0\) ตัวเลข \(-0.42\) ตัวเลข \(168.79\). กำหนดให้ \(\mathbb{R}\) แทนเซตของจำนวนจริง. ดังนั้น สัญกรณ์ เช่น \(x \in \mathbb{R}\) ระบุว่า ตัวแปร \(x\) เป็นสเกล่าร์ของจำนวนจริง.
เวกเตอร์ (vector) หมายถึง ลำดับของตัวเลข. เวกเตอร์ ในพีชคณีตเชิงเส้น มีสองชนิด คือ เวกเตอร์แนวนอน และเวกเตอร์แนวตั้ง. เวกเตอร์แนวนอน แสดงด้วยลำดับในแนวนอน เช่น
\([103.4, \; -28.6, \; 0, \; 9.99]\) เป็นเวกเตอร์แนวนอน ที่เป็นลำดับของตัวเลขสี่ตัว. ตำราเล่มนี้จะใช้เวกเตอร์แนวตั้งเป็นหลัก นั่นคือ หากกล่าวถึง เวกเตอร์ โดยไม่ได้ระบุเฉพาะเจาะจงแล้ว จะหมายถึง เวกเตอร์แนวตั้ง ที่แสดงด้วยลำดับในแนวตั้ง ดังแสดงใน สมการ \(\eqref{eq: linalg vector}\) \[\begin{eqnarray}
\boldsymbol{x} = \begin{bmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{bmatrix}
\label{eq: linalg vector}
\end{eqnarray}\] เมื่อ \(x_1, \ldots, x_n\) แทนตัวเลขสเกล่าร์ และ \(x_i\) เรียกว่าเป็น ส่วนประกอบที่ \(i\) ของเวกเตอร์ \(\boldsymbol{x}\). สัญกรณ์ เช่น \(\boldsymbol{x} \in \mathbb{R}^n\) ระบุว่า ตัวแปร \(\boldsymbol{x}\) เป็นเวกเตอร์ ที่มีส่วนประกอบจำนวน \(n\) ตัว ซึ่งส่วนประกอบแต่ละตัวเป็นจำนวนจริง. หมายเหตุ สัญลักษณ์ \(\boldsymbol{0}\) หมายถึง เวกเตอร์ที่ส่วนประกอบทุกตัวเป็นศูนย์. นั่นคือ \(\boldsymbol{0} = [0, 0, \ldots, 0]^T\).
เมทริกซ์ (matrix) หมายถึง โครงสร้างสองมิติของลำดับของตัวเลข ดังแสดงในสมการ \(\eqref{eq: linalg matrix}\) \[\begin{eqnarray} \boldsymbol{A} = \begin{bmatrix} A_{11} & A_{12} & \cdots & A_{1n} \\ A_{21} & A_{22} & \cdots & A_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ A_{m1} & A_{m2} & \cdots & A_{mn} \\ \end{bmatrix} \label{eq: linalg matrix} \end{eqnarray}\] เมื่อ \(\boldsymbol{A}\) เป็นเมทริกซ์ขนาดมิติ \(m \times n\) และ \(A_{11}, \ldots, A_{mn}\) แทนตัวเลขสเกล่าร์ และ \(A_{ij}\) เป็น ส่วนประกอบของเมทริกซ์ ที่ดัชนีตำแหน่ง แถว \(i\) และสดมภ์ \(j\). ดัชนี อาจเขียนโดยใช้ตัวห้อย โดยมีเครื่องหมายจุลภาคคั่น เช่น \(A_{i,j}\) หรือเครื่องหมายจุลภาคคั่นอาจถูกละไว้ได้ เช่น \(A_{ij}\) ในกรณีที่ความหมายชัดเจน. เมทริกซ์สามารถถูกระบุขนาดมิติ ได้จาก สัญกรณ์ \(\boldsymbol{A} \in \mathbb{R}^{m \times n}\).
นอกจากนี้ ศาสตร์การเรียนรู้ของเครื่อง นิยมใช้สัญกรณ์จุดคู่ ดังปฏิบัติใน . นั่นคือ กำหนดให้ สัญกรณ์ \(\boldsymbol{A}_{i,:}\) หมายถึง เมทริกซ์ย่อย ที่ได้จากส่วนประกอบที่แถว \(i\) ของเมทริกซ์ \(\boldsymbol{A}\) คือ \(\boldsymbol{A}_{i,:} = [A_{i1}, \; A_{i2}, \; \ldots, \; A_{in}]\) เรียกว่า แถว \(i\) ของ \(\boldsymbol{A}\). ทำนองเดียวกัน สัญกรณ์ \(\boldsymbol{A}_{:,j}\) หมายถึง เมทริกซ์ย่อย ที่ได้จากส่วนประกอบที่สดมภ์ \(j\) ของเมทริกซ์ \(\boldsymbol{A}\) เรียกว่า สดมภ์ \(j\) ของ \(\boldsymbol{A}\).
การสลับเปลี่ยน (transpose) เป็นการดำเนินการจัดเรียงลำดับใหม่. สำหรับเวกเตอร์ การสลับเปลี่ยนของเวกเตอร์แนวนอน จะได้เวกเตอร์แนวตั้ง และการสลับเปลี่ยนของเวกเตอร์แนวตั้ง จะได้เวกเตอร์แนวนอน และใช้สัญกรณ์ เช่น \(\boldsymbol{x}^T\) คือ การสลับเปลี่ยนของเวกเตอร์ \(\boldsymbol{x}\) เช่น จากสมการ \(\eqref{eq: linalg vector}\) เวกเตอร์ \(\boldsymbol{x}^T = [x_1, \; x_2, \; \ldots, \; x_n]\) หรือ ในทางกลับกัน สมการ \(\eqref{eq: linalg vector}\) อาจเขียนใหม่ได้ในรูป \(\boldsymbol{x} = [x_1, \; x_2, \; \ldots, \; x_n]^T\)
สำหรับเมทริกซ์ การสลับเปลี่ยนของเมทริกซ์ ซึ่งใช้สัญกรณ์ เช่น \(\boldsymbol{A}^T\) คือ การเปลี่ยนตำแหน่งของส่วนประกอบ โดย ส่วนประกอบที่ตำแหน่ง \((i,j)\) จะถูกเปลี่ยนไปอยู่ตำแหน่ง \((j,i)\) ซึ่งผลที่ได้เสมือนกับการสลับตำแหน่งรอบแนวทะแยงมุมของเมทริกซ์. สมการ \(\eqref{eq: linalg transpose}\) แสดงการสลับเปลี่ยนของเมทริกซ์ \(\boldsymbol{A}\). \[\begin{eqnarray} \boldsymbol{A}^T = \begin{bmatrix} A_{11} & A_{21} & \cdots & A_{m1} \\ A_{12} & A_{22} & \cdots & A_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ A_{1n} & A_{2n} & \cdots & A_{mn} \\ \end{bmatrix} \label{eq: linalg transpose} \end{eqnarray}\] การสลับเปลี่ยนของเมทริกซ์ จะทำให้ขนาดมิติของเมทริกซ์เปลี่ยนไป เช่น จากตัวอย่าง ขนาดมิติของเมทริกซ์ \(\boldsymbol{A}\) คือ \(m \times n\) แต่ ขนาดมิติของเมทริกซ์ \(\boldsymbol{A}^T\) คือ \(n \times m\) (สังเกตจาก \(\boldsymbol{A}^T\) มี \(n\) แถว และ \(m\) สดมภ์)
2.1.0.0.1 มิติ และลำดับชั้น.
โครงสร้างของเวกเตอร์ มีหนึ่งมิติของลำดับ ในลักษณะที่ลำดับของข้อมูลดำเนินไปได้แนวเดียว. โครงสร้างของเมทริกซ์ มีสองมิติ ในลักษณะที่ลำดับของข้อมูลดำเนินไปได้สองแนว. ภาพขาวดำ 2 หรือภาพสเกลเทา (gray-scale image) ก็มีลักษณะโครงสร้างสองมิติของลำดับ นั่นคือ มีโครงสร้างสองมิติของลำดับค่าพิกเซล ตามลำดับแนวตั้ง และตามลำดับแนวนอน. การเขียนโปรแกรมจะใช้โครงสร้างข้อมูล เช่น อาร์เรย์ (array) ขนาดสองมิติ ในการแทนข้อมูลภาพสเกลเทานี้.
ข้อมูลอาจมีโครงสร้างมิติของลำดับที่ซับซ้อนมากได้. ภาพสี (color image) มีโครงสร้างสามมิติของลำดับค่าพิกเซล ตามลำดับแนวตั้ง ตามลำดับแนวนอน และตามชุดของช่องสี แดง เขียว น้ำเงิน. (แม้ช่องสีไม่ได้มีความสัมพันธ์ในเชิงลำดับ ในลักษณะที่ช่องสีแดง ไม่จำเป็นต้องมาก่อนช่องสีเขียว เป็นต้น แต่ข้อมูลของช่องสีต่าง ๆ แยกออกเป็นลักษณะของตัวเอง). การเขียนโปรแกรมจะใช้โครงสร้างข้อมูล เช่น อาร์เรย์ ขนาดสามมิติ ในการแทนข้อมูลภาพสี. ข้อมูลวิดีโอ (video) เป็นข้อมูลเป็นลักษณะโครงสร้างสี่มิติของลำดับค่าพิกเซล ตามลำดับแนวตั้ง ตามลำดับแนวนอน ตามชุดของช่องสี และตามลำดับเวลา. การเขียนโปรแกรมจะใช้โครงสร้างข้อมูล เช่น อาร์เรย์ ขนาดสี่มิติ ในการแทนข้อมูลวิดีโอ และข้อมูลวิดีโอ ที่กล่าวถึงนี้ ยังไม่ได้รวมข้อมูลช่องเสียงด้วย ซึ่งหากเป็นช่องเสียงเดี่ยว (monophonic sound channel) ก็ต้องการมิติของอาร์เรย์อีกหนึ่งมิติ หรือหากเป็นช่องเสียงสเตอริโอ (steriophonic sound channel) ก็ต้องการมิติของอาร์เรย์อีกสองมิติ หรือหากแยกช่องเสียงพูด ออกจากเสียงประกอบอื่น ๆ หรือมีข้อมูลคำบรรยายภาษาต่าง ๆ ประกอบ ก็ต้องการมิติของอาร์เรย์เพิ่มขึ้นอีก.
อย่างไรก็ตาม หากกล่าวถึง “มิติ” นั้นจะสังเกตว่า ภาพสเกลเทาสองมิติ เป็นข้อมูลโครงสร้างลำดับสองมิติ. ภาพสีสองมิติ เป็นข้อมูลโครงสร้างลำดับสามมิติ. วิดีโอ (ของภาพสองมิติไม่รวมข้อมูลเสียง) เป็นข้อมูลโครงสร้างลำดับสี่มิติ. นอกจากนั้น เมื่อกล่าวถึง ปริภูมิค่า (vector space) ซึ่ง ใช้บอกถึง ขนาดความเป็นไปได้ของลักษณะข้อมูล และ มิติของปริภูมิจะใช้บอกขนาด และความซับซ้อนของปริภูมินั้น ๆ เช่น ข้อมูลสเกล่าร์ที่เป็นค่าจริง จะมีปริภูมิค่า เป็น \(\mathbb{R}\) เป็นปริภูมิค่าหนึ่งมิติ. แต่ละจุดข้อมูล อ้างถึงได้ด้วยตัวเลขตัวเดียว. การค้นหาจุดข้อมูลที่สนใจ ในปริภูมิ ทำได้โดยการค้นหาบนเส้นจำนวนจริง. ข้อมูลเวกเตอร์ที่มีส่วนประกอบเป็นค่าจริงสองค่า จะมีปริภูมิค่า เป็น \(\mathbb{R}^2\). แต่ละจุดข้อมูล อ้างถึงได้ด้วยตัวเลขสองตัว. การค้นหาจุดข้อมูลที่สนใจ ในปริภูมิ ทำได้โดยการค้นหาบนระนาบจำนวนจริง. ข้อมูลเวกเตอร์ที่มีส่วนประกอบเป็นค่าจริงสี่ค่า จะมีปริภูมิค่า เป็น \(\mathbb{R}^4\). แต่ละจุดข้อมูล อ้างถึงได้ด้วยตัวเลขสี่ตัว. การค้นหาจุดข้อมูลที่สนใจ ในปริภูมิ ทำได้โดยการค้นหาในปริภูมิขนาดสี่มิติ. ข้อมูลเมทริกซ์ขนาด \(2 \times 2\) จะมีปริภูมิค่า เป็น \(\mathbb{R}^{2\times2}\). แต่ละจุดข้อมูล อ้างถึงได้ด้วยตัวเลขสี่ตัว. การค้นหาจุดข้อมูลที่สนใจ ในปริภูมิ ทำได้โดยการค้นหาบนปริภูมิขนาดสี่มิติ เช่นเดียวกับ ข้อมูลเวกเตอร์ที่มีส่วนประกอบสี่ค่าจริง. นั่นคือ เวกเตอร์ที่มีส่วนประกอบสี่ค่าจริง มีความสามารถในการแทนข้อมูลเทียบเท่ากับ เมทริกซ์ขนาด \(2 \times 2\) เพียงแต่ ข้อมูลที่เก็บในเวกเตอร์ที่มีส่วนประกอบสี่ค่าจริง ไม่ได้มีโครงสร้างลำดับ เหมือนกับ ข้อมูลที่เก็บในเมทริกซ์ขนาด \(2 \times 2\) และโครงสร้างลำดับเช่นนี้ โดยเฉพาะหากเป็นโครงสร้างตามธรรมชาติของข้อมูล สามารถนำมาใช้ในประโยชน์ และช่วยในการรู้จำรูปแบบอย่างมีประสิทธิภาพได้ (ดังเช่น ที่จะได้อภิปรายในบท [chapter: Deep Learning] ต่อไป)
อย่างไรก็ตาม เพื่อลดความสับสน จากนี้ไป เมื่อกล่าวถึง “มิติ” จะมีการระบุอย่างชัดเจนว่า หมายถึง มิติในความหมายใด เช่น คำว่า มิติ ใช้ในความหมาย มุมมอง ซึ่งเป็นเป็นความหมายกว้าง ๆ ของมิติ และใช้ในความหมายของมิติโดยทั่วไป. คำว่า มิติปริภูมิค่า ใช้ในความหมายของ มิติของปริภูมิค่า และคำว่า ลำดับชั้น (rank) ใช้ในความหมายของ มิติของโครงสร้างลำดับ. ตัวอย่าง ภาพสเกลเทาขนาด \(600 \times 800\) พิกเซล เป็น ภาพสองมิติ ที่เป็นข้อมูลลำดับชั้นสอง (มีลำดับตามแนวตั้ง และตามแนวนอน) หรือสามารถแทนด้วย เมทริกซ์ ขนาดมิติ \(600 \times 800\) และมีมิติปริภูมิค่า เป็น \(480000\). สัญกรณ์ \(\{0, \ldots, 255\}^{ุ600 \times 800}\) จะระบุชัดเจนทั้งจากมุมมองของลำดับชั้น และมิติปริภูมิค่า. นอกจากนั้น สัญกรณ์นี้ยังระบุช่วงค่าที่เป็นไปได้ของข้อมูลด้วย ว่า แต่ละค่าเป็นจำนวนเต็มที่มีค่าระหว่าง \(0\) ถึง \(255\).
เทนเซอร์ (tensor) หมายถึง โครงสร้างลำดับชั้นของตัวเลข. สเกล่าร์ คือ เทนเซอร์ ลำดับชั้นศูนย์ (rank-0 tensor). เวกเตอร์ คือ เทนเซอร์ ลำดับชั้นหนึ่ง (rank-1 tensor). เมทริกซ์ คือ เทนเซอร์ ลำดับชั้นสอง (rank-2 tensor). ข้อมูลที่แทนด้วยอาร์เรย์ขนาด \(n\) มิติ คือ เทนเซอร์ ลำดับชั้น \(n\) (rank-n tensor). ตัวเลขแต่ละตัวในเทนเซอร์ เป็น ส่วนประกอบของเทนเซอร์ และอ้างอิงได้โดยใช้ดัชนี ตามลำดับชั้น.
ตัวอย่าง เทนเซอร์ลำดับชั้นสี่ \(\boldsymbol{A} \in \mathbb{R}^{1 \times 2 \times 2 \times 3}\) มีค่า \[\boldsymbol{A} = \begin{bmatrix} \begin{bmatrix} [[1.2], \; [3]] & [[-8.7], \; [6]] \end{bmatrix} & \begin{bmatrix} [[0.9], \; [-1]] & [[4], \; [1]] \end{bmatrix} & \begin{bmatrix} [[11], \; [5]] & [[0.1], \; [0]] \end{bmatrix} \end{bmatrix}\] และ \(A_{1,1,1,1} = 1.2\); \(A_{1,1,1,2} = 0.9\); ... \(A_{1,2,2,2} = 1\); \(A_{1,2,2,3} = 0\).
หมายเหตุ รูปแบบอักษรที่ใช้ คือ ฟังก์ชันจะใช้สัญลักษณ์ เช่น \(f\) หรือ \(\sigma\) หรือ \(\mathrm{calc}\) โดยไม่มีการทำแบบอักษรตัวหนา ไม่ว่าฟังก์ชันจะให้ค่าออกมาเป็นสเกล่าร์ หรือเมทริกซ์ หรือเทนเซอร์ เช่น \(f: \mathbb{R} \rightarrow \mathbb{R}\) และ \(\sigma: \mathbb{R}^n \rightarrow \mathbb{R}^{m_1 \times m_2 \times m_3}\) และ \(\mathrm{calc}: \mathbb{R}^{n \times m} \rightarrow \mathbb{R}^q\). สัญกรณ์ เช่น \(f: \rho_1 \rightarrow \rho_2\) ระบุว่าฟังก์ชัน \(f\) รับค่าตัวแปรที่อยู่ในเซต \(\rho_1\) เพื่อไปทำการคำนวณ และให้ผลลัพธ์การคำนวณออกมาเป็นค่าที่อยู่ในเซต \(\rho_2\). ตัวอย่างเช่น \(g: \mathbb{R}^n \rightarrow \mathbb{R}\) จะบอกว่า ฟังก์ชัน \(g\) รับตัวแปรเข้าเป็นเวกเตอร์ที่มี \(n\) ส่วนประกอบ และจะให้ผลลัพธ์ออกมาเป็นสเกล่าร์.
2.1.0.0.2 การคำนวณเมทริกซ์.
การบวกลบเมทริกซ์กับเมทริกซ์ จะทำได้ ก็ต่อเมื่อ เมทริกซ์มีขนาดมิติเท่ากัน และผลลัพธ์คำนวณได้จากค่าของส่วนประกอบทั้งสองที่ตำแหน่งเดียวกัน เช่น \(\boldsymbol{C} = \boldsymbol{A} + \boldsymbol{B}\) โดย \(C_{ij} = A_{ij} + B_{ij}\). การคำนวณสเกล่าร์กับเมทริกซ์ กำหนดให้ เป็นการคำนวณค่าสเกล่าร์นั้น ๆ กับส่วนประกอบของเมทริกซ์แต่ละตัว เช่น \(\boldsymbol{D} = a \cdot \boldsymbol{B} + c\) โดย \(D_{ij} = a \cdot B_{ij} + c\). การคำนวณเวกเตอร์กับเวกเตอร์ และการคำนวณสเกล่าร์กับเวกเตอร์ ก็ทำในทำนองเดียวกัน. (ดูตัวอย่าง จากแบบฝึกหัด [ex: linalg addition python])
2.1.0.0.3 การคูณกันของเมทริกซ์.
การคูณเมทริกซ์ (matrix product) จะดำเนินการได้ เมื่อเมทริกซ์สองเมทริกซ์ที่จะคูณกัน ต้องมีขนาดมิติที่เข้ากันได้ นั่นคือ จำนวนสดมภ์ของเมทริกซ์ตัวหน้า เท่ากับ จำนวนแถวของเมทริกซ์ตัวหลัง และใช้สัญกรณ์ เช่น \(\boldsymbol{A} \boldsymbol{B}\) หรือ \(\boldsymbol{A} \cdot \boldsymbol{B}\) โดย เมทริกซ์ \(\boldsymbol{A}\) มีขนาดมิติ \(m \times p\) เมทริกซ์ \(\boldsymbol{B}\) มีขนาดมิติ \(p \times n\) และ ผลลัพธ์ \(\boldsymbol{C} = \boldsymbol{A} \cdot \boldsymbol{B}\) จะมีขนาดมิติ \(m \times n\) และ \(C_{ij} = \sum_k A_{ik} \cdot B_{kj}\).
นอกจากการคูณเมทริกซ์แล้ว การดำเนินการ การคูณแบบตัวต่อตัว (element-wise product หรือ Hadamard product) ก็มีการใช้อย่างกว้างขวาง. การคูณแบบตัวต่อตัว จะดำเนินการได้ ก็ต่อเมื่อ เมทริกซ์สองเมทริกซ์ที่จะคูณกัน ต้องมีขนาดมิติที่เท่ากัน และใช้สัญกรณ์ เช่น \(\boldsymbol{A} \odot \boldsymbol{B}\) โดย เมทริกซ์ \(\boldsymbol{A}\) มีขนาดมิติ \(m \times n\) เมทริกซ์ \(\boldsymbol{B}\) มีขนาดมิติ \(m \times n\) และ ผลลัพธ์ \(\boldsymbol{C} = \boldsymbol{A} \odot \boldsymbol{B}\) จะมีขนาดมิติ \(m \times n\) และ \(C_{ij} = A_{ij} \cdot B_{ij}\). การคูณกันของเวกเตอร์ จะแสดงเสมือนกับการดำเนินการเมทริกซ์ เช่น \(z = \boldsymbol{x}^T \cdot \boldsymbol{y}\) เมื่อ \(\boldsymbol{x}\) และ \(\boldsymbol{y}\) มีสัดส่วนเท่ากัน และ \(z = \sum_i x_i \cdot y_i\). สังเกต \(z = \boldsymbol{x}^T \cdot \boldsymbol{y} = \boldsymbol{y}^T \cdot \boldsymbol{x}\). (ดูตัวอย่าง จากแบบฝึกหัด [ex: linalg matrix mult python])
2.1.0.0.4 คุณสมบัติของการคูณเมทริกซ์.
การคูณเมทริกซ์ มีคุณสมบัติการกระจาย (distributive properties) เช่น \(\boldsymbol{A} (\boldsymbol{B} + \boldsymbol{C}) = \boldsymbol{A} \boldsymbol{B} + \boldsymbol{A} \boldsymbol{C}\) มีคุณสมบัติการเปลี่ยนกลุ่ม (associative properties) เช่น \(\boldsymbol{A} (\boldsymbol{B} \boldsymbol{C}) = (\boldsymbol{A} \boldsymbol{B}) \boldsymbol{C}\) แต่ การคูณเมทริกซ์ไม่มีคุณสมบัติการสลับที่.
2.1.1 ระบบสมการ
เมทริกซ์ เวกเตอร์ และการดำเนินการต่าง ๆ ที่กล่าวมา นอกจากจะช่วยการอ้างถึง และการจัดการกับข้อมูลทำได้อย่างสะดวกแล้ว ยังอำนวยความสะดวกในการอ้างถึง และจัดการกับปัญหาระบบสมการ หรือปัญหาที่มีตัวแปรไม่ทราบค่า และสมการที่เกี่ยวข้องจำนวนมาก ตัวอย่าง เช่น \[\begin{eqnarray} x + y + z &=& 6 \label{eq: lin alg ex 1} \\ 2 x + 2 y - z &=& 3 \label{eq: lin alg ex 2} \\ y + z &=& 5 \label{eq: lin alg ex 3} \end{eqnarray}\] เป็นระบบสมการเชิงเส้น และสามารถเขียนได้กระทัดรัด ด้วยสัญกรณ์ ของเมทริกซ์ และเวกเตอร์ ดังนี้ \[\begin{eqnarray} \begin{bmatrix} 1 & 1 & 1 \\ 2 & 2 & -1 \\ 0 & 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 6 \\ 3 \\ 5 \end{bmatrix} \nonumber \end{eqnarray}\] และกระทัดรัดขึ้นอีก เป็น \[\begin{eqnarray} \boldsymbol{A} \boldsymbol{x} = \boldsymbol{b} \label{eq: lin alg example lin sys} \end{eqnarray}\] หาก นิยาม \[\begin{eqnarray} \boldsymbol{A} = \begin{bmatrix} 1 & 1 & 1 \\ 2 & 2 & -1 \\ 0 & 1 & 1 \end{bmatrix} \mbox{ นิยาม } \boldsymbol{x} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} \mbox{ และนิยาม } \boldsymbol{b} = \begin{bmatrix} 6 \\ 3 \\ 5 \end{bmatrix} \label{eq: lin alg matrix example} \end{eqnarray}\]
เมทริกซ์เอกลักษณ์ (identity matrix) ที่นิยมใช้สัญญลักษณ์ \(\boldsymbol{I}\) (หรือ \(\boldsymbol{I}_n\) เมื่อต้องการระบุขนาดมิติ \(n \times n\)) เป็นเมทริกซ์ที่มีค่าตามแนวทะแยงมุมเป็นหนึ่ง และค่าอื่น ๆ เป็นศูนย์ เช่น เมทริกซ์เอกลักษณ์ ขนาดมิติ \(3 \times 3\) คือ \[\boldsymbol{I} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]
เมทริกซ์เอกลักษณ์ มีคุณสมบัติสำคัญ คือ เมื่อคูณกับเมทริกซ์ใด หรือคูณกับเวกเตอร์ใด แล้วจะได้เมทริกซ์นั้น หรือเวกเตอร์นั้น ตัวเดิม. นั่นคือ \(\boldsymbol{A} \cdot \boldsymbol{I} = \boldsymbol{A}\).
เมทริกซ์ผกผัน (matrix inverse) คือ เมทริกซ์คู่คูณ ที่เมื่อคูณกับคู่ของมันแล้ว ผลลัพธ์จะได้เป็นเมทริกซ์เอกลักษณ์ ใช้สัญญลักษณ์เป็นเมทริกซ์ที่มีตัวยกลบหนึ่ง เช่น \(\boldsymbol{A}^{-1}\) หมายถึง เมทริกซ์ผกผัน ที่เป็นคู่ผกผันกับ \(\boldsymbol{A}\) นั่นคือ \(\boldsymbol{A}^{-1} \cdot \boldsymbol{A} = \boldsymbol{I}\). จากตัวอย่าง เมทริกซ์ผกผัน ที่เป็นคู่ของ \(\boldsymbol{A}\) ในสมการ \(\eqref{eq: lin alg matrix example}\) คือ \[\begin{eqnarray} \boldsymbol{A}^{-1} = \begin{bmatrix} 1 & 0 & -1 \\ -0.6666667 & 0.3333333 & 1 \\ 0.6666667 & -0.3333333 & 0 \end{bmatrix} \label{eq: lin alg example inv} \end{eqnarray}\] จากเมทริกซ์ผกผัน สมการ \(\eqref{eq: lin alg example lin sys}\) สามารถแก้ได้โดย \(\boldsymbol{x} = \boldsymbol{A}^{-1} \boldsymbol{b}\) ซึ่งเมื่อแทนค่าเข้าไป จะได้ \(\boldsymbol{x} = [1, \; 2, \; 3]^T\) ซึ่งหมายถึง ตัวแปร \(x = 1\) ตัวแปร \(y = 2\) และตัวแปร \(z = 3\). (ตัวอย่างวิธีการหาเมทริกซ์ผกผัน สามารถดูได้จากแบบฝึกหัด [ex: linalg mat inverse])
2.1.1.0.1 ความเป็นอิสระเชิงเส้น.
สังเกตว่า ระบบสมการในตัวอย่างข้างต้น (สมการ \(\eqref{eq: lin alg ex 1}\) ถึง \(\eqref{eq: lin alg ex 3}\)) มีสามสมการ และมีตัวแปรที่ไม่ทราบค่า (unknown variables) สามตัว ซึ่งทำให้เมทริกซ์สัมประสิทธิ์ \(\boldsymbol{A}\) (สมการ \(\eqref{eq: lin alg matrix example}\)) มีจำนวนแถวเท่ากับจำนวนสดมภ์ ซึ่งเรียกว่า เมทริกซ์จตุรัส (square matrix).
โดยทั่วไปแล้ว ถ้าหากมีจำนวนสมการน้อยเกินไป (จำนวนแถวของเมทริกซ์ น้อยกว่า จำนวนสดมภ์ หรือ เมทริกซ์ที่มีสัดส่วนเตี้ยกว้าง) คำตอบของระบบสมการจะมีได้หลายค่า เช่น ตัวอย่างระบบสมการ \[\begin{eqnarray} x + y + z &=& 6 \nonumber \\ 2 x + 2 y - z &=& 3 \nonumber \end{eqnarray}\] จะได้ \[\begin{eqnarray} \boldsymbol{A} = \begin{bmatrix} 1 & 1 & 1 \\ 2 & 2 & -1 \end{bmatrix} \mbox{ เวกเตอร์ตัวแปร } \boldsymbol{x} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} \mbox{ และเวกเตอร์ค่าคงที่ } \boldsymbol{b} = \begin{bmatrix} 6 \\ 3 \end{bmatrix} \nonumber \end{eqnarray}\] ซึ่งมีคำตอบหลายชุด เช่น \(x = 1, y = 2, z = 3\) หรือ \(x = 2, y = 1, z = 3\) หรือ \(x = 3, y = 0, z = 3\) หรือ \(x = 2.5, y = 0.5, z = 3\) เป็นต้น. (จริง ๆ คือ ทุกชุดค่า ที่ \(x + y = 3\) และ \(z = 3\) สามารถเป็นคำตอบได้ทั้งหมด)
แต่หากมีจำนวนสมการน้อยเกินไป (จำนวนแถวของเมทริกซ์ มากกว่า จำนวนสดมภ์ หรือ เมทริกซ์ที่มีสัดส่วนสูงแคบ) อาจจะไม่สามารถหาคำตอบของระบบสมการได้ เช่น ตัวอย่างระบบสมการ \[\begin{eqnarray} x + y + z &=& 6 \label{eq: lin alg example long mat 1} \\ 2 x + 2 y - z &=& 3 \label{eq: lin alg example long mat 2} \\ y + z &=& 5 \label{eq: lin alg example long mat 3} \\ x + z &=& 5 \label{eq: lin alg example long mat 4} \end{eqnarray}\] จะได้ \[\begin{eqnarray} \boldsymbol{A} = \begin{bmatrix} 1 & 1 & 1 \\ 2 & 2 & -1 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{bmatrix} \mbox{ เวกเตอร์ตัวแปร } \boldsymbol{x} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} \mbox{ และเวกเตอร์ค่าคงที่ } \boldsymbol{b} = \begin{bmatrix} 6 \\ 3 \\ 5 \\ 5 \end{bmatrix} \nonumber \end{eqnarray}\] ซึ่งไม่สามารถหาคำตอบของสมการได้ (สังเกตว่า \(x = 1, y = 2, z = 3\) ที่เป็นคำตอบของสามสมการแรก \(\eqref{eq: lin alg example long mat 1}\) ถึง \(\eqref{eq: lin alg example long mat 3}\) ขัดแย้งกับสมการที่สี่ \(\eqref{eq: lin alg example long mat 4}\))
2.1.1.0.2 เมทริกซ์เอกฐาน.
ถึงแม้ เมทริกซ์จะเป็นเมทริกซ์จตุรัส ก็ไม่ใช่ทุกเมทริกซ์จตุรัส ที่จะสามารถหาเมทริกซ์ผกผันคู่ของมันได้. เมทริกซ์ที่หาคู่ผกผันไม่ได้ จะเรียกว่า เมทริกซ์เอกฐาน (singular matrix). เช่น ตัวอย่างระบบสมการ \[\begin{eqnarray} x + y + z &=& 6 \label{eq: lin alg example singular 1} \\ 2 x + 2 y + 2 z &=& 12 \label{eq: lin alg example singular 2} \\ y + z &=& 5 \label{eq: lin alg example singular 3} \end{eqnarray}\] จะได้ \[\begin{eqnarray} \boldsymbol{A} = \begin{bmatrix} 1 & 1 & 1 \\ 2 & 2 & 2 \\ 0 & 1 & 1 \end{bmatrix} \mbox{ เวกเตอร์ตัวแปร } \boldsymbol{x} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} \mbox{ และเวกเตอร์ค่าคงที่ } \boldsymbol{b} = \begin{bmatrix} 6 \\ 12 \\ 5 \end{bmatrix} \nonumber \end{eqnarray}\] เมทริกซ์สัมประสิทธิ์ที่ได้จะเป็นเมทริกซ์เอกฐาน. สังเกต สมการแรก \(\eqref{eq: lin alg example singular 1}\) กับสมการที่สอง \(\eqref{eq: lin alg example singular 2}\) จะเห็นว่า สมการที่สอง มีค่าเท่ากับสมการแรกคูณสอง ซึ่งหมายความว่า ถึงแม้จะมีสองสมการ แต่ก็ให้ข้อมูลเทียบเท่ากับการมีแค่สมการเดียว และสัมประสิทธิ์ของสมการ ทำให้ \(\boldsymbol{A}_{1,:}\) และ \(\boldsymbol{A}_{2,:}\) ไม่เป็นอิสระเชิงเส้นแก่กัน. (ดูแบบฝึกหัด [ex: lin alg lin equation nxn repeat column] สำหรับตัวอย่างของสดมภ์ไม่เป็นอิสระเชิงเส้นแก่กัน)
เซตของเวกเตอร์ \(\{\boldsymbol{v}_1, \boldsymbol{v}_2, \ldots, \boldsymbol{v}_k\}\) จะเป็นอิสระเชิงเส้นกัน (linearly independent) ถ้า \[\begin{eqnarray} a_1 \boldsymbol{v}_1 + a_2 \boldsymbol{v}_2 + \ldots + a_k \boldsymbol{v}_k = \boldsymbol{0} \nonumber \end{eqnarray}\] ก็ต่อเมื่อ ทุก ๆ ค่าสัมประสิทธิ์ \(a_1, \ldots, a_k\) ต้องเป็นศูนย์ทั้งหมดเท่านั้น.
นอกจากความสัมพันธ์เชิงเส้นระหว่างเวกเตอร์แล้ว ถ้ามีสเกล่าร์ \(a_1, a_2, \ldots, a_k\) ที่ทำให้ \(\boldsymbol{v} = a_1 \boldsymbol{v}_1 + a_2 \boldsymbol{v}_2 + \ldots + a_k \boldsymbol{v}_k\) แล้วจะเรียกว่า \(\boldsymbol{v}\) เป็นผลรวมเชิงเส้น ของ \(\boldsymbol{v}_1, \boldsymbol{v}_2, \ldots, \boldsymbol{v}_k\). การที่แถวใดของเมทริกซ์ เป็นผลรวมเชิงเส้นของแถวอื่น ๆ ก็จะทำให้เมทริกซ์เป็นเอกฐาน.
2.1.1.0.3 ดีเทอร์มิแนนต์.
ลักษณะเฉพาะที่สำคัญอย่างหนึ่งของเมทริกซ์จตุรัส คือ ดีเทอร์มิแนนต์ (determinant). ค่าของดีเทอร์มิแนนต์สามารถช่วยบอกได้ว่าเมทริกซ์จตุรัสนั้นเป็นเอกฐานหรือไม่.
ดีเทอร์มิแนนต์ของเมทริกซ์จตุรัส \(\boldsymbol{A}\) ขนาดมิติ \(n \times n\) เป็นค่าสเกล่าร์ และใช้สัญญลักษณ์ เช่น \(|\boldsymbol{A}|\) หรือ \(\mathrm{det}\; \boldsymbol{A}\) โดย ดีเทอร์มิแนนต์ มีคุณสมบัติ
ดีเทอร์มิแนนต์ ของเมทริกซ์ \(\boldsymbol{A}\) เป็นฟังก์ชันเชิงเส้นของแต่ละสดมภ์ของ \(\boldsymbol{A}\). นั่นคือ ถ้า \(\boldsymbol{A}=[\boldsymbol{a}_1, \; \boldsymbol{a}_2, \; \ldots, \; \boldsymbol{a}_n]\) เมื่อ \(\boldsymbol{a}_i\) เป็นสดมภ์ที่ \(i^{th}\) ของเมทริกซ์ แล้ว \[\begin{eqnarray} \;& \; & \mathrm{det}\; [\boldsymbol{a}_1, \; \ldots, \boldsymbol{a}_{k-1}, \; \alpha \boldsymbol{a}_k + \beta \boldsymbol{v}, \; \boldsymbol{a}_{k+1}, \; \ldots, \; \boldsymbol{a}_n] \nonumber \\ \;& \; & = \alpha \cdot \mathrm{det}\; [\boldsymbol{a}_1, \; \ldots, \boldsymbol{a}_{k-1}, \; \boldsymbol{a}_k, \; \boldsymbol{a}_{k+1}, \; \ldots, \; \boldsymbol{a}_n] \nonumber \\ \;& \; & + \beta \cdot \mathrm{det}\; [\boldsymbol{a}_1, \; \ldots, \boldsymbol{a}_{k-1}, \; \boldsymbol{v}, \; \boldsymbol{a}_{k+1}, \; \ldots, \; \boldsymbol{a}_n] \label{eq: lin alg det prop 1} \end{eqnarray}\] เมื่อ \(\alpha\) และ \(\beta\) เป็นจำนวนจริงใด ๆ และ \(\boldsymbol{v} \in \mathbb{R}^n\) เป็นเวกเตอร์ที่มีส่วนประกอบเป็น \(n\) ค่าจริงใด ๆ
ถ้ามีสดมภ์ที่มีค่าเท่ากัน ค่าดีเทอร์มิแนนต์จะเป็นศูนย์. นั่นคือ ถ้ามี \(\boldsymbol{a}_i = \boldsymbol{a}_j\) โดย \(i \neq j\) แล้ว \[\begin{eqnarray} \mathrm{det}\; [\boldsymbol{a}_1, \; \ldots, \boldsymbol{a}_i, \; \ldots, \boldsymbol{a}_j, \; \ldots, \; \boldsymbol{a}_n] = \mathrm{det}\; [\boldsymbol{a}_1, \; \ldots, \boldsymbol{a}_i, \; \ldots, \boldsymbol{a}_i, \; \ldots, \; \boldsymbol{a}_n] = 0 \label{eq: lin alg det prop 2} \end{eqnarray}\]
ค่าดีเทอร์มิแนนต์ ของเมทริกซ์เอกลักษณ์ เป็นหนึ่ง. นั่นคือ \[\begin{eqnarray} \mathrm{det}\; \boldsymbol{I} = 1 \label{eq: lin alg det prop 3} \end{eqnarray}\]
จากคุณสมบัติพื้นฐานทั้งสาม ทฤษฎีการขยายปัจจัยร่วม (cofactor expansion theorem) ถูกพัฒนาขึ้น และ ค่าดีเทอร์มิแนนต์ ของเมทริกซ์ \(\boldsymbol{A}\) ขนาดมิติ \(n \times n\) สามารถคำนวณได้จาก \[\begin{eqnarray} \mathrm{det}\; \boldsymbol{A} &=& A_{k1} \cdot C_{k1} + A_{k2} \cdot C_{k2} + \ldots + A_{kn} \cdot C_{kn} \nonumber \\ &=& A_{1k} \cdot C_{1k} + A_{2k} \cdot C_{2k} + \ldots + A_{nk} \cdot C_{nk} \nonumber \\ &=& \sum_j A_{kj} \cdot C_{kj} = \sum_j A_{ik} \cdot C_{ik} \label{eq: lin alg det cofactor} \end{eqnarray}\] เมื่อ \(k\) เป็นดัชนีที่เลือกตรึงให้คงที่ (\(k \in \{1, \ldots, n\}\)) และ ปัจจัยร่วม (cofactor) \(C_{ij} = (-1)^{i+j} \cdot M_{ij}\) โดย \(M_{ij}\) เป็นค่าดีเทอร์มิแนนต์ของเมทริกซ์ย่อยจาก \(\boldsymbol{A}\) โดยการตัดแถวที่ \(i\) และตัดสดมภ์ที่ \(j\) ออก. ตัวอย่าง \[\begin{eqnarray} \boldsymbol{A} = \begin{bmatrix} 1 & 4 & 3 \\ 8 & 2 & 7 \\ 0 & 5 & 9 \end{bmatrix} \mbox{ เมื่อเลือกตรึงแถว } k = 1 \mbox{ จะได้ } \mathrm{det}\; \boldsymbol{A} = 1 \cdot \begin{vmatrix} 2 & 7 \\ 5 & 9 \end{vmatrix} -4 \cdot \begin{vmatrix} 8 & 7 \\ 0 & 9 \end{vmatrix} + 3 \cdot \begin{vmatrix} 8 & 2 \\ 0 & 5 \end{vmatrix} \nonumber \end{eqnarray}\] และ \[\begin{vmatrix} 2 & 7 \\ 5 & 9 \end{vmatrix} = 2 \cdot |9| - 7 \cdot |5| = -17. \; \begin{vmatrix} 8 & 7 \\ 0 & 9 \end{vmatrix} = 8 \cdot |9| - 7 \cdot |0| = 72. \; \begin{vmatrix} 8 & 2 \\ 0 & 5 \end{vmatrix} = 8 \cdot |5| - 2 \cdot |0| = 40.\] ดังนั้น \(\mathrm{det}\; \boldsymbol{A} = -17 -4 \cdot 72 + 3 \cdot 40 = -185.\)
คุณสมบัติที่ตามมาของดีเทอร์มิแนนต์ มีหลายอย่าง แต่ที่สำคัญ คือ \(\mathrm{det}\; \boldsymbol{A} = \mathrm{det}\; \boldsymbol{A}^T\) ดังนั้น การที่ระบบสมการมีสมการที่ไม่เป็นอิสระเชิงเส้นต่อกัน (แถวของเมทริกซ์ ไม่เป็นอิสระเชิงเส้นต่อกัน) จะทำให้ เมทริกซ์สัมประสิทธิ์ มีค่าดีเทอร์มิแนนต์เป็นศูนย์ ซึ่งหมายถึง เมทริกซ์เป็นเอกฐาน.
2.1.1.0.4 นอร์ม.
ดีเทอร์มิแนนต์่ บอกคุณสมบัติที่สำคัญของเมทริกซ์จัตุรัส. เวกเตอร์ก็ต้องการค่าบอกคุณสมบัติ. นอร์ม (norm) เป็นการวัดขนาดของเวกเตอร์. จำนวนส่วนประกอบของเวกเตอร์ อาจจะบอกขนาดมิติปริภูมิของเวกเตอร์ แต่นอร์มจะบอกขนาดของเวกเตอร์ และเป็นคุณสมบัติที่สำคัญอันหนึ่งของเวกเตอร์ สามารถใช้เปรียบเทียบสองเวกเตอร์ที่อยู่ปริภูมิค่าเดียวกัน (เวกเตอร์ที่อยู่ปริภูมิค่าเดียวกัน จะมีจำนวนส่วนประกอบเท่ากัน แต่อาจมีขนาดไม่เท่ากัน). นอร์มอาจวัดได้หลายวิธี แต่วิธีที่นิยม คือ \(L^p\) นอร์ม โดย \(L^p\) นอร์ม กำหนดเป็น \[\begin{eqnarray} \|\boldsymbol{x}\|_p = \left(\sum_i |x_i|^p \right)^{\frac{1}{p}} \end{eqnarray}\] เมื่อ \(p \in \mathbb{R}, p \geq 1\).
งานส่วนใหญ่มักเลือกใช้ \(L^2\) นอร์ม (\(p=2\)) หรือเรียกว่า ยูคลีเดียนนอร์ม (Euclidean norm) หรือ ระยะทางยูคลีเดียน (Euclidean distance) ที่ใช้สัญกรณ์ \(\|\boldsymbol{x}\|_2\). ความนิยมของ \(L^2\) นอร์ม ทำให้บ่อยครั้ง สัญกรณ์อาจละตัวห้อยออก เป็น \(\|\boldsymbol{x}\|\). นอกจากนั้น บางครั้ง เพื่อความสะดวกและลดการคำนวณ ค่า \(L^2\) นอร์มกำลังสอง ได้แก่ \(\|\boldsymbol{x}\|_2^2 = \sum_i x_i^2 = \boldsymbol{x}^T \cdot \boldsymbol{x}\) ก็นิยมใช้วัดขนาดเวกเตอร์
ตัวอย่างเช่น \(\boldsymbol{v} = [0.5,\; -8, \; 11]^T\) จะมี \(L^2\) นอร์มเป็น \(\|\boldsymbol{v}\| = \sqrt{\sum_i v_i^2}\) \(= \sqrt{0.25 + 64 + 121}\) \(= 13.61\). สังเกตว่า ส่วนประกอบที่มีค่าใกล้ ๆ ศูนย์ จะมีขนาดผลเล็กลง เมื่อคำนวณด้วย \(L^2\) นอร์ม (สังเกต ส่วนประกอบ \(0.5\) มีขนาดผลลดลงเป็น \(0.25\)) ดังนั้น สำหรับบางภาระกิจที่ไม่ต้องการพฤติกรรมเช่นนี้ แต่ต้องการ พฤติกรรมที่ผลของส่วนประกอบมีอัตราส่วนคงที่ ซึ่งจะช่วยให้เห็นความแตกต่างระหว่างศูนย์ กับค่าที่ไม่เป็นศูนย์ได้ดีกว่า ภาระกิจเหล่านั้นอาจเลือกใช้ \(L^1\) นอร์ม ตัวอย่างเช่น \(\|\boldsymbol{v}\|_1\) \(= \sum_i |v_i|\) \(=0.5 + 8 + 11\) = \(19.5\).
เวกเตอร์ใดก็ตามที่มี \(L^2\) นอร์มเป็นหนึ่ง จะเรียกว่า เวกเตอร์หนึ่งหน่วย (unit vector) นั่นคือ ถ้า \(\| \boldsymbol{u} \|_2 = 1\) จะเรียกว่า \(\boldsymbol{u}\) เป็นเวกเตอร์หนึ่งหน่วย. ตัวอย่าง เช่น เวกเตอร์ \(\boldsymbol{v}_1 = [1, 0, 0]^T\) เวกเตอร์ \(\boldsymbol{v}_2 = [0, 0, 1]^T\) และเวกเตอร์ \(\boldsymbol{v}_3 = [0.7428, 0.5571, -0.3714]^T\) เป็นเวกเตอร์หนึ่งหน่วย. แต่เวกเตอร์ \(\boldsymbol{v}_4 = [1, 1, 0]^T\) (ขนาดเป็น \(1.414\)) และเวกเตอร์ \(\boldsymbol{v}_5 = [0.7, 0.2, 0.1]^T\) (ขนาดเป็น \(0.735\)) ไม่ใช่เวกเตอร์หนึ่งหน่วย.
เวกเตอร์ใด ๆ \(\boldsymbol{v} \in \mathbb{R}^n\) จะมีเวกเตอร์หนึ่งหน่วย \(\boldsymbol{u} \in \mathbb{R}^n\) ที่ชี้ไปทิศทางเดียวกับมัน และ \[\begin{eqnarray} \boldsymbol{u} = \frac{\boldsymbol{v}}{\|\boldsymbol{v}\|} \label{eq: linalg unit vec} \end{eqnarray}\] จากตัวอย่างข้างต้น เวกเตอร์ \(\boldsymbol{v}_4 = [1, 1, 0]^T\) มีีเวกเตอร์หนึ่งหน่วย \([ 0.7071, 0.7071, 0]^T\) ที่ชี้ไปทางเดียวกับมัน และเวกเตอร์ \(\boldsymbol{v}_5 = [0.7, 0.2, 0.1]^T\) มีีเวกเตอร์หนึ่งหน่วย \([0.9526, 0.2722, 0.1361]^T\) ที่ชี้ไปทางเดียวกับมัน.
2.1.2 ภาพฉายเชิงตั้งฉาก
การเปลี่ยนมุมมอง รวมถึงการแยกปัจจัยประกอบออก เป็นหนึ่งในวิธีที่ช่วยในการทำความเข้าใจเรื่องราวต่าง ๆ รวมถึงการทำความเข้าใจกลุ่มของตัวแปรต่าง ๆ และทำความเข้าใจข้อมูล. การทำภาพฉายเชิงตั้งฉาก เป็นเสมือนการเปลี่ยนมุมมองวิธีหนึ่ง
รูป 1.2 แสดงตัวอย่างการทำภาพฉายเชิงตั้งฉาก. เวกเตอร์ \(\boldsymbol{x} = [3, \; 4]^T\) เมื่อฉายลงบนทิศทางของของเวกเตอร์ \(\boldsymbol{u} = [1, \; 0]^T\) แล้ว จะมีขนาดเป็น \(3\) บนทิศทางของ \(\boldsymbol{u}\) และเมื่อฉายลงบน \(\boldsymbol{v} = [0,\; 1]^T\) จะมีขนาดเป็น \(4\) บนทิศทางของ \(\boldsymbol{v}\). ขนาดของการฉายเวกเตอร์ใด ๆ \(\boldsymbol{z}\) ลงบนทิศทางของเวกเตอร์หนึ่งหน่วย \(\boldsymbol{u}\) จะคำนวณได้จาก \[\begin{eqnarray} z_u = \boldsymbol{z}^T \boldsymbol{u} \label{eq: linalg vector projection} \end{eqnarray}\] เมื่อ \(z_u\) เป็นขนาดของเวกเตอร์ \(\boldsymbol{z}\) ที่ฉายลงบนทิศทางของเวกเตอร์หนึ่งหน่วย \(\boldsymbol{u}\).
รูป 1.3 แสดงตัวอย่างการทำภาพฉายเชิงตั้งฉากของเวกเตอร์เดิม \(\boldsymbol{x} = [3, 4]^T\) แต่ฉายลงบนเวกเตอร์ \(\boldsymbol{u} = [0.9578, 0.2873]^T\) และเวกเตอร์ \(\boldsymbol{v} = [-0.2873, 0.9578]^T\). ดังนั้น ขนาดของ \(\boldsymbol{x}\) ที่ฉายลงบน \(\boldsymbol{u}\) จะเป็น \(\boldsymbol{x}^T \boldsymbol{u}\) \(=4.023\) และขนาดที่ฉายลงบน \(\boldsymbol{u}\) จะเป็น \(\boldsymbol{x}^T \boldsymbol{u}\) \(=2.969\). สังเกตว่า ในตัวอย่างนี้ เวกเตอร์ \(\boldsymbol{v}\) ตั้งฉากกับเวกเตอร์ \(\boldsymbol{u}\) และเวกเตอร์ที่ตั้งฉากกัน (orthogonal vectors) จะมีผลคูณเวกเตอร์เป็นศูนย์ หรือ \(\boldsymbol{v}^T \boldsymbol{u} = 0\).
การแปลงเชิงเส้น (linear transformation) ก็คือการคูณตัวแปรที่ต้องการแปลง ด้วยเมทริกซ์แปลง (transformation matrix). นั่นคือ การแปลงเชิงเส้น \(T(\boldsymbol{x}) = \boldsymbol{A} \boldsymbol{x}\). การหาเวกเตอร์ตั้งฉาก อาจมองเป็นการแปลงเวกเตอร์ไปเป็นเวกเตอร์ที่ตั้งฉากกับต้นฉบับ ซึ่งตัวอย่างข้างต้นนี้ใช้เมทริกซ์แปลง \[\begin{eqnarray} \boldsymbol{A} = \begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix} \nonumber \end{eqnarray}\] และจากตัวอย่าง \(\boldsymbol{u} = [0.9578, 0.2873]^T\) ซึ่งเมื่อทำการแปลงเชิงเส้นด้วย \(\boldsymbol{A} \boldsymbol{u} = [-0.2873, 0.9578]^T\) ผลลัพธ์คือเวกเตอร์ที่ตั้งฉากกับเวกเตอร์ต้นฉบับ.
![fig: การฉายภาพ. (ก) การฉายภาพของเวกเตอร์ \boldsymbol{x} = [a, b]^T ลงบนเวกเตอร์ \boldsymbol{u} = [1, 0]^T คือ การฉายภาพจากเวกเตอร์ที่สนใจ ในแนวตั้งฉากไปลงบน แนวของกับเวกเตอร์ที่ฉายลง และ (ข) การฉายภาพของเวกเตอร์ \boldsymbol{x}= [a, b]^T ลงบน เวกเตอร์ \boldsymbol{u}=[1,0]^T กับเวกเตอร์ \boldsymbol{v}=[0,1]^T โดยมีขนาดเป็น a เมื่อฉายบนเวกเตอร์ \boldsymbol{u} และมีขนาดเป็น b เมื่อฉายบนเวกเตอร์ \boldsymbol{v}. ทั้ง \boldsymbol{u} และ \boldsymbol{v} เป็นเวกเตอร์หนึ่งหน่วย.](02Background/linalg/orthoproj1a_xOntoU.png) |
![fig: การฉายภาพ. (ก) การฉายภาพของเวกเตอร์ \boldsymbol{x} = [a, b]^T ลงบนเวกเตอร์ \boldsymbol{u} = [1, 0]^T คือ การฉายภาพจากเวกเตอร์ที่สนใจ ในแนวตั้งฉากไปลงบน แนวของกับเวกเตอร์ที่ฉายลง และ (ข) การฉายภาพของเวกเตอร์ \boldsymbol{x}= [a, b]^T ลงบน เวกเตอร์ \boldsymbol{u}=[1,0]^T กับเวกเตอร์ \boldsymbol{v}=[0,1]^T โดยมีขนาดเป็น a เมื่อฉายบนเวกเตอร์ \boldsymbol{u} และมีขนาดเป็น b เมื่อฉายบนเวกเตอร์ \boldsymbol{v}. ทั้ง \boldsymbol{u} และ \boldsymbol{v} เป็นเวกเตอร์หนึ่งหน่วย.](02Background/linalg/orthoproj1a_xOntoUV.png) |
| ก | ข |
![เวกเตอร์ \boldsymbol{x} = [3, 4]^T ฉายลงบน เวกเตอร์หนึ่งหน่วย \boldsymbol{u} = [0.9578, 0.2873]^T และ \boldsymbol{v} = [-0.2873, 0.9578]^T โดย \boldsymbol{a} เป็นเวกเตอร์ตามทิศทาง \boldsymbol{u} แต่มีขนาดเท่ากับที่เวกเตอร์ \boldsymbol{x} ฉายลงบน \boldsymbol{u} และทำนองเดียวกัน \boldsymbol{b} ก็เป็นเวกเตอร์ที่ได้จากการฉาย \boldsymbol{x} ลงบน \boldsymbol{v}. นั่นคือ \boldsymbol{a} = 4.023 \boldsymbol{u} =[3.853, 1.156]^T และ \boldsymbol{b} = 2.969 \boldsymbol{v} =[-0.853, 2.844]^T.](02Background/linalg/orthoproj2b_vec.png)
เวกเตอร์ \(\boldsymbol{x} \in \mathbb{R}^n\) เรียกว่า \(\boldsymbol{x}\) อยู่ในปริภูมิ \(\mathbb{R}^n\) นั่นคือ ถ้า \(\mathbb{R}^n\) เป็นเสมือนแผนที่ เวกเตอร์ \(\boldsymbol{x}\) ใด ๆ ที่อยู่ในปริภูมิ ก็เปรียบเสมือนเป็นจุด ๆ หนึ่งบนแผนที่นั้น. จุดใด ๆ ในปริภูมิ \(\mathbb{R}^n\) จะสามารถอ้างอิงถึงได้โดยใช้ตัวเลข \(n\) ตัว (นั่นคือ \(n\) มิติปริภูมิค่า)
2.1.2.0.1 ปริภูมิย่อย.
เซตย่อย (subset) \(\rho\) ของ \(\mathbb{R}^n\) จะเป็นปริภูมิย่อย (subspace) ของ \(\mathbb{R}^n\) เมื่อ \(\rho\) เป็นเซตปิด (closed set) ภายใต้การดำเนินการบวกของเวกเตอร์ และการคูณกับสเกล่าร์. นั่นคือ ถ้า \(\boldsymbol{a}\) และ \(\boldsymbol{b}\) เป็นเวกเตอร์ในปริภูมิย่อย \(\rho\) แล้ว \(\boldsymbol{a} + \boldsymbol{b}\) และ \(\alpha \boldsymbol{a}\) ก็ต้องอยู่ในปริภูมิย่อย \(\rho\) สำหรับทุก ๆ ค่า \(\alpha\).
ตัวอย่าง เช่น จากรูป 1.3 เวกเตอร์ \(\boldsymbol{x}\) อยู่ใน \(\mathbb{R}^2\) และเวกเตอร์ \(\boldsymbol{u}\) และเวกเตอร์ \(\boldsymbol{v}\) และเวกเตอร์ \(\boldsymbol{a}\) และเวกเตอร์ \(\boldsymbol{b}\) ก็อยู่ในปริภูมิ \(\mathbb{R}^2\) ด้วย. สมมติให้ \(\rho_1\) เป็นปริภูมิย่อยของ \(\mathbb{R}^2\) โดยมี เวกเตอร์ \(\boldsymbol{u}\) อยู่ใน \(\rho_1\) แต่ไม่มีเวกเตอร์ \(\boldsymbol{v}\) ในปริภูมิย่อย \(\rho_1\). นั่นคือ ปริภูมิย่อย \(\rho_1\) เป็นเซตปิด สำหรับ เวกเตอร์ในแนว \(\boldsymbol{u}\) เช่น \(\boldsymbol{u}\) และ \(\boldsymbol{a}\) อยู่ใน \(\rho_1\).
มองจากอีกมุมหนึ่ง ถ้ากำหนดให้ \(\{\boldsymbol{c}_1, \boldsymbol{c}_2, \ldots, \boldsymbol{c}_k\}\) เป็นเซตของเวกเตอร์ใด ๆ ในปริภูมิ \(\mathbb{R}^n\) แล้ว ผลรวมเชิงเส้นทุกแบบของเวกเตอร์เหล่านี้ จะเป็นเซตของเวกเตอร์ ที่เรียกว่า การแผ่ทั่ว (span) ของเวกเตอร์ \(\boldsymbol{c}_1, \boldsymbol{c}_2, \ldots, \boldsymbol{c}_k\) และใช้สัญกรณ์ 3
\[\begin{eqnarray} \mathrm{span}[\boldsymbol{c}_1, \; \boldsymbol{c}_2, \; \ldots, \; \boldsymbol{c}_k] = \left\{ \sum_{i-1}^k \alpha_i \boldsymbol{c}_i : \alpha_1, \ldots, \alpha_k \in \mathbb{R} \right\} \end{eqnarray}\] และ ปริภูมิย่อยคือ การแผ่ทั่วของเซตของเวกเตอร์. ตัวอย่างเช่น ปริภูมิย่อย \(\rho_1\) ในตัวอย่างข้างต้น ก็คือการแผ่ทั่วของ \(\{\boldsymbol{u}\}\) และปริภูมิ \(\mathbb{R}^2\) ก็คือการแผ่ทั่วของ \(\{\boldsymbol{u}, \boldsymbol{v}\}\).
สังเกตว่าในขณะที่ การอ้างถึงตำแหน่งบนปริภูมิ \(\mathbb{R}^2\) ต้องการตัวเลข \(2\) ตัว (สองมิติปริภูมิค่า) แต่การอ้างถึงตำแหน่งบนปริภูมิย่อย \(\rho_1\) ต้องการตัวเลขแค่ตัวเดียว (ปริภูมิย่อย มีหนึ่งมิติปริภูมิค่า). จำนวนมิติปริภูมิค่า ของปริภูมิใด ๆ (รวมถึงปริภูมิย่อยใด ๆ) จะเท่ากับจำนวนของเวกเตอร์ที่เป็นอิสระเชิงเส้นกัน ที่อยู่ในปริภูมิ. ตัวอย่างเช่น ปริภูมิ \(\mathbb{R}^2\) มีสองเวกเตอร์ที่เป็นอิสระเชิงเส้น ไม่ว่าจะเลือก \(\boldsymbol{u}\) กับ \(\boldsymbol{v}\) หรือเลือกชุด \([1, 0]^T\) กับ \([1, 1]^T\) หรือเลือกชุด \([1, -1]^T\) กับ \([0, 1]^T\) หรือชุดอื่น ๆ ของเวกเตอร์สองตัวที่ตั้งฉากกัน. ดังนั้น \(\mathbb{R}^2\) จึงมีสองมิติ(ปริภูมิค่า). ปริภูมิ \(\rho_1\) มีแค่เวกเตอร์เดียวที่เป็นอิสระเชิงเส้น ดังนั้น \(\rho_1\) จึงมีหนึ่งมิติ(ปริภูมิค่า).
2.1.2.0.2 การแยกส่วนประกอบเชิงตั้งฉาก.
ถ้ากำหนด \(\rho\) เป็นปริภูมิย่อยของ \(\mathbb{R}^n\) และกำหนดให้ \(\rho^\perp\) เป็นส่วนเติมเต็มเชิงตั้งฉาก (orthogonal complement) ของ \(\rho\) โดย \(\rho^\perp\) ประกอบด้วยเวกเตอร์ทั้งหมด ที่แต่ละเวกเตอร์ตั้งฉากกับทุกเวกเตอร์ใน \(\rho\). นั่นคือ \[\begin{eqnarray} \rho^\perp = \{ \boldsymbol{x} : \boldsymbol{x}^T \boldsymbol{v} = 0 \mbox{ for all } \boldsymbol{v} \in \rho \} \end{eqnarray}\]
เซต \(\rho^\perp\) เองก็เป็นปริภูมิย่อยของ \(\mathbb{R}^n\) ด้วย. เวกเตอร์ทั้งหมดจากทั้งสองเซต \(\rho\) และ \(\rho^\perp\) แผ่ทั่ว \(\mathbb{R}^n\). นั่นคือ เวกเตอร์ใด ๆ \(\boldsymbol{x} \in \mathbb{R}^n\) สามารถแยกส่วนประกอบออกได้ \[\begin{eqnarray} \boldsymbol{x} = \boldsymbol{x}_1 + \boldsymbol{x}_2 \nonumber \end{eqnarray}\] เมื่อ \(\boldsymbol{x}_1 \in \rho\) และ \(\boldsymbol{x}_2 \in \rho^\perp\). การแยกส่วนประกอบแบบนี้ จะเรียกว่า การแยกส่วนประกอบเชิงตั้งฉาก (orthogonal decomposition) ของ \(\boldsymbol{x}\) ตาม \(\rho\) และ \(\boldsymbol{x}_1\) และ \(\boldsymbol{x}_2\) เป็นภาพฉายตั้งฉาก (orthogonal projections) ของ \(\boldsymbol{x}\) ลงบนปริภูมิย่อย \(\rho\) และ \(\rho^\perp\).
จากตัวอย่างในรูป 1.3 จะเห็นว่า \[\begin{eqnarray} \boldsymbol{x} &=& [3, 4]^T = \boldsymbol{a} + \boldsymbol{b} \nonumber \\ &=& 4.023 \boldsymbol{u} + 2.969 \boldsymbol{v} \nonumber \end{eqnarray}\] หรือ \(\boldsymbol{x}\) ถูกแยกออก เป็น ส่วนประกอบแรก \(4.023\) และส่วนประกอบที่สอง \(2.969\). หัวข้อ [sec: PCA] อภิปรายวิธีการวิเคราะห์ส่วนประกอบหลัก (Principal Component Analysis) ซึ่งเป็นวิธีที่ใช้แนวคิดหลัก จากการฉายภาพเชิงตั้งฉาก เพื่อลดมิติปริภูมิของข้อมูล ซึ่งจะช่วยการประมวลผล และช่วยการนำเสนอภาพของข้อมูลได้
2.1.3 เวกเตอร์ลักษณะเฉพาะและค่าลักษณะเฉพาะ
การแปลงข้อมูลเชิงเส้นมีการใช้อย่างกว้างขวาง และเครื่องมือสำคัญที่นิยมใช้ในการวิเคราะห์การแปลงข้อมูลเชิงเส้น คือ เวกเตอร์ลักษณะเฉพาะ และ ค่าลักษณะเฉพาะ.
กำหนดให้ \(\boldsymbol{A}\) เป็น \(n \times n\) เมทริกซ์. ค่าสเกล่าร์ \(\lambda\) และเวกเตอร์ \(\boldsymbol{v}\) โดย \(\boldsymbol{v} \neq \boldsymbol{0}\) จะเรียกว่า ค่าลักษณะเฉพาะ (eigenvalue) และเวกเตอร์ลักษณะเฉพาะ (eigenvector) ของ \(\boldsymbol{A}\) เมื่อ \[\begin{eqnarray} \boldsymbol{A} \boldsymbol{v} = \lambda \boldsymbol{v} \label{eq: linalg eigen} \end{eqnarray}\]
ตัวอย่าง เช่น \[\begin{eqnarray} \boldsymbol{A} = \begin{bmatrix} 9.8 & 3.6 \\ 3.6 & 2.5 \end{bmatrix} \nonumber \end{eqnarray}\] มีค่าลักษณะเฉพาะค่าหนึ่ง คือ \(\lambda_1 = 11.277\) และมีเวกเตอร์ลักษณะเฉพาะที่คู่กัน \(\boldsymbol{v}_1 = [-0.925, -0.379]^T\). เมื่อตรวจสอบ จะพบว่าทางซ้ายมือ (\(\boldsymbol{A} \boldsymbol{v}\)) จะได้ \[\begin{eqnarray} \begin{bmatrix} 9.8 & 3.6 \\ 3.6 & 2.5 \end{bmatrix} \cdot \begin{bmatrix} -0.925 \\ -0.379 \end{bmatrix} = \begin{bmatrix} -10.433 \\ -4.279 \end{bmatrix} \nonumber \end{eqnarray}\] ซึ่ง เท่ากับทางขวามือ คือ \(\lambda_1 \cdot \mathbf{v}_1\). ดังนั้น \(\lambda_1\) และ \(\mathbf{v}_1\) คือ ค่าลักษณะเฉพาะ และเวกเตอร์ลักษณะเฉพาะ ของ \(\boldsymbol{A}\).
2.1.3.0.1 การหาค่าลักษณะเฉพาะและเวกเตอร์ลักษณะเฉพาะ.
จาก \(\boldsymbol{A} \boldsymbol{v} = \lambda \boldsymbol{v}\) ดังนั้น \((\boldsymbol{A} - \lambda \boldsymbol{I}) \boldsymbol{v} = \boldsymbol{0}\) เมื่อ \(\boldsymbol{I}\) เป็นเมทริกซ์เอกลักษณ์. กรณีที่ \(\boldsymbol{v} = \boldsymbol{0}\) เป็นกรณีที่ชัดเจนแต่ไม่น่าสนใจ (trivial). พิจารณากรณีที่ \(\boldsymbol{v} \neq \boldsymbol{0}\) สำหรับกรณีนี้ \(\mathrm{det} [\boldsymbol{A} - \lambda \boldsymbol{I}] = 0\) (เพราะว่า ถ้าดีเทอร์มิแนนต์นี้ไม่เท่ากับศูนย์ จะแก้สมการได้เป็น \(\boldsymbol{v} = [\boldsymbol{A} - \lambda \boldsymbol{I}]^{-1} \boldsymbol{0} = \boldsymbol{0}\) ซึ่งจะเป็นกรณีแรก ที่ชัดเจนแต่ไม่น่าสนใจ)
จาก \(\mathrm{det} [\boldsymbol{A} - \lambda \boldsymbol{I}] = 0\) แทนค่าและแก้สมการหาค่า \(\lambda\) แล้วใช้ค่า \(\lambda\) ที่ได้แทนค่าลงใน \((\boldsymbol{A} - \lambda \boldsymbol{I}) \boldsymbol{v} = \boldsymbol{0}\) และแก้สมการหาค่าของเวกเตอร์ \(\boldsymbol{v}\).
เช่น จากตัวอย่างข้างต้น \[\begin{eqnarray} \mathrm{det} \begin{bmatrix} 9.8 - \lambda & 3.6 \\ 3.6 & 2.5 - \lambda \end{bmatrix} &=& 0 \nonumber \\ (3.6)(3.6) - (9.8 - \lambda)(2.5 - \lambda) &=& 0 \nonumber \\ \lambda^2 - 12.3 \lambda + 11.54 &=& 0 \nonumber \end{eqnarray}\] จะได้เป็นสมการพหุนาม (polynomial equation) ของตัวแปร \(\lambda\) ที่ในตัวอย่างนี้เป็นสมการกำลังสอง (quadratic equation) ซึ่งมีรูปทั่วไปคือ \(a x^2 + b x + c = 0\) และผลเฉลยของสมการ มีสองค่าคือ \(x_1 = \frac{-b+\sqrt{b^2 - 4 a c}}{2 a}\) และ \(x_2 = \frac{-b-\sqrt{b^2 - 4 a c}}{2 a}\) และเมื่อแทนค่า \(a = 1, b = -12.3, c = 11.54\) แล้วจะได้ค่าลักษณะเฉพาะสองค่าคือ \(\lambda_1 = 11.28\) และ \(\lambda_2 = 1.02\). นำค่าลักษณะเฉพาะแต่ละค่า ไปหาเวกเตอร์ที่คู่กัน ได้แก่ สำหรับ \(\lambda_1 = 11.28\) คำนวณหาเวกเตอร์ลักษณะเฉพาะ \(\boldsymbol{v}_1\) จาก \[\begin{eqnarray} \underbrace{\begin{bmatrix} 9.8 & 3.6 \\ 3.6 & 2.5 \end{bmatrix}}_{\boldsymbol{A}} \cdot \underbrace{\begin{bmatrix} a \\ b \end{bmatrix}}_{\boldsymbol{v}_1} &=& \underbrace{11.28}_{\lambda_1} \cdot \underbrace{\begin{bmatrix} a \\ b \end{bmatrix}}_{\boldsymbol{v}_1} \nonumber \end{eqnarray}\] และจะได้สมการ \[\begin{eqnarray} 9.8 a + 3.6 b &=& 11.28 a \nonumber \\ 3.6 a + 2.5 b &=& 11.28 b \nonumber \end{eqnarray}\] ซึ่งสองสมการนี้ไม่เป็นเชิงเส้นต่อกัน (เพราะว่า นี่คือ กรณี \(\mathrm{det} [\boldsymbol{A} - \lambda \boldsymbol{I}] = 0\)) ดังนั้น คำตอบที่ได้จะไม่ได้มีแค่หนึ่งเดียว. สมมติเลือกสมการแรกมา \(9.8 a + 3.6 b = 11.28 a\) และแก้สมการจะได้ \(b = 0.41 a\) ดังนั้นเวกเตอร์ลักษณะเฉพาะคือ \([1, 0.41]^T\) หรือ \([2, 0.82]^T\) หรือ \([3, 1.32]^T\) หรือ เวกเตอร์ใด ๆ ที่อยู่ในรูป \(\alpha [1, 0.41]^T\) เมื่อ \(\alpha\) เป็นจำนวนจริงใด ๆ ที่ \(\alpha \neq 0\). สังเกตว่า เวกเตอร์ทั้งหมดที่ได้จะชี้ไปทิศทางเดียวกัน (หรือตรงกันข้ามก็ได้ แต่ไม่ชี้ไปทางอื่น) แต่ต่างขนาดกันเท่านั้น.
เพื่อความสะดวก เวกเตอร์ลักษณะเฉพาะมักจะเลือกให้เป็นเวกเตอร์ขนาดหนึ่งหน่วย. ดังนั้น จากเวกเตอร์ \([1, 0.41]^T\) จะได้เวกเตอร์หนึ่งหน่วยเป็น \(\frac{1}{\sqrt{1^2 + 0.41^2}} [1, 0.41]^T\) \(=[0.93, 0.38]^T\). นั่นคือ ได้เวกเตอร์ลักษณะเฉพาะ \(\boldsymbol{v}_1 = [0.93, 0.38]^T\) คู่กับค่าลักษณะเฉพาะ \(\lambda_1 = 11.28\) และในทำนองเดียวกัน ได้เวกเตอร์ลักษณะเฉพาะ \(\boldsymbol{v}_2 = [0.38, -0.93]^T\) คู่กับค่าลักษณะเฉพาะ \(\lambda_2 = 1.02\). หมายเหตุ ถึงแม้จะเลือกเวกเตอร์ลักษณะเฉพาะ ให้เป็นเวกเตอร์หนึ่งหน่วยแล้วก็ตาม แต่เวกเตอร์ลักษณะเฉพาะก็ยังอาจเลือกได้หลายแบบอยู่ เช่น \(\boldsymbol{v}_1 = [-0.93, -0.38]^T\) หรือ \(\boldsymbol{v}_2 = [-0.38, 0.93]^T\) ที่อยู่ในแนวเดียวกัน มีขนาดเป็นหนึ่งเหมือนกัน เพียงแต่มีทิศตรงกันข้าม.
2.2 ความน่าจะเป็น
ปัจจัยสำคัญเรื่องหนึ่ง โดยเฉพาะกับงานการรู้จำรูปแบบและการเรียนรู้ของเครื่อง คือความไม่แน่นอน (uncertainty). ความไม่แน่นอนอาจจะมาจากหลายสาเหตุ เช่น ความไม่เที่ยงของเครื่องมือ หรือวิธีการวัด หรือวิธีการเก็บข้อมูล หรืออาจมาจากสัญญาณรบกวน หรือมาจากขนาดของข้อมูลที่จำกัด หรือแม้แต่ธรรมชาติความหลากหลายและความแปรปรวนของข้อมูลเอง. ทฤษฎีความน่าจะเป็น (probability theory) เป็นแนวทางหนึ่งที่ให้กรอบวิธีการสำหรับการวัด และการจัดการกับความไม่แน่นอน. ดังนั้น ทฤษฎีความน่าจะเป็น 4 จึงเป็นพื้นฐานที่สำคัญสำหรับการเรียนรู้ของเครื่องและการรู้จำรู้แบบ.
2.2.1 เซต
ทฤษฎีความน่าจะเป็นจะมองรูปแบบต่าง ๆ เป็นเหตุการณ์ (event) และทฤษฎีความน่าจะเป็นจะใช้เซตในการอธิบายความหมายของเหตุการณ์.
เซต (set) แทนกลุ่มของค่าต่าง ๆ ที่สนใจ. เซต อาจแสดงด้วยสัญกรณ์ เช่น \(\{24, 98, 16, 53 \}\) ที่หมายถึง เซตที่มีสมาชิกสี่ตัว ได้แก่ ค่า \(24\) ค่า \(98\) ค่า \(16\) และค่า \(53\) โดยลำดับของสมาชิกที่ปรากฎในเซตไม่ได้มีความหมาย ซึ่งต่างจากลำดับของส่วนประกอบในเวกเตอร์ เมทริกซ์ หรือเทนเซอร์ ที่อภิปรายในหัวข้อ 1.1. นอกจากนั้นสมาชิกของเซต ก็ไม่ได้จำกัดเฉพาะตัวเลข ตัวอย่างเช่น \(\{ \mbox{`ธ'}, \mbox{`ท'}, \mbox{`ถ'}, \mbox{`ต'}, \mbox{`ด'}\}\) เป็นเซตของพยัญชนะห้าตัว. สัญกรณ์ เช่น \(a \in A\) ระบุว่า \(a\) เป็นสมาชิกของเซต \(A\).
ถ้าเซต \(A\) มีสมาชิกที่ทุกตัว เป็นสมาชิกของเซต \(B\) แล้วจะเรียกว่า เซต \(A\) เป็นเซตย่อย (subset) ของเซต \(B\) และใช้สัญกรณ์ \(A \subset B\). นั่นคือ ถ้า \(A \subset B\) แล้ว \(a \in A\) หมายถึง \(a \in B\) ด้วย แต่อาจมีสมาชิกของ \(B\) ที่ไม่ได้เป็นสมาชิกของ \(A\) ก็ได้. สัญกรณ์ \(b \notin A\) หมายถึง ค่า \(b\) ไม่ได้เป็นสมาชิกของเซต \(A\). สัญลักษณ์ \(\emptyset\) จะใช้แทนเซตว่าง (empty set) หรือเซตที่ไม่มีสมาชิกอยู่. นั่นคือ \(\emptyset = \{ \}\). สัญลักษณ์ \(\Omega\) มักใช้แทนเซตของค่าที่เป็นไปได้ทั้งหมด.
2.2.1.0.1 การดำเนินการเซต.
อินเตอร์เซกชัน (intersection) แทนด้วยสัญกรณ์ เช่น \(A \cap B\) ซึ่งหมายถึง การดำเนินการที่ผลลัพธ์จะเป็นเซตที่มีสมาชิกที่เป็นทุกสมาชิกของ \(A\) และ \(B\) ที่มีค่าเหมือนกัน. นั่นคือ ถ้า \(a \in A\) และ \(b \in B\) และ \(a = b\) แล้ว \(a \in A \cap B\) และในทางกลับกัน ถ้า \(c \in A \cap B\) แล้ว \(c \in A\) และ \(c \in B\).
ยูเนียน (union) แทนด้วยสัญกรณ์ เช่น \(A \cup B\) ซึ่งหมายถึง การดำเนินการที่ผลลัพธ์จะเป็นเซตที่มีสมาชิกทั้งหมดของ \(A\) และสมาชิกทั้งหมดของ \(B\). นั่นคือ ถ้า \(a \in A\) แล้ว \(a \in A \cup B\) และถ้า \(b \in B\) แล้ว \(b \in A \cup B\) และในทางกลับกัน ถ้า \(c \in A \cup B\) แล้ว \(c \in A\) หรือ \(c \in B\) หรือทั้ง \(c \in A\) และ \(c \in B\).
ผลต่างเซต (set difference) แทนด้วยสัญกรณ์ เช่น \(A \setminus B\) ซึ่งหมายถึง การดำเนินการที่ผลลัพธ์จะเป็น เซตที่สมาชิกทั้งหมด เป็นสมาชิกของ \(A\) แต่ไม่มีสักตัวที่เป็นสมาชิกของ \(B\). นั่นคือ ถ้า \(c \in A \setminus B\) แล้ว \(c \in A\) และ \(c \notin B\) และในทางกลับกัน ถ้า \(a \in A\) และ \(a \notin B\) แล้ว \(a \in A \setminus B\).
ส่วนเติมเต็ม (complement) แทนด้วยสัญกรณ์ เช่น \(A^c\) ซึ่งหมายถึง เซตของค่าทั้งหมดที่เป็นไปได้ แต่ไม่ได้เป็นสมาชิกของ \(A\). นั่นคือ \(A^c = \Omega \setminus A\).
ตัวอย่างเช่น ถ้า \(A = \{1, 3, 8, 9, 12, 16, 20\}\) และ \(B = \{7, 8, 12, 20, 32\}\) แล้วจะได้
\(A \cap B = \{8, 12, 20\}\) และ \(A \cup B = \{1, 3, 7, 8, 9, 12, 16, 20, 32\}\) และ \(A \setminus B = \{1, 3, 9, 16\}\) และ \(B \setminus A = \{7, 32\}\).
2.2.2 ความน่าจะเป็น
ความน่าจะเป็น (probability) เป็นค่าที่ใช้ประมาณโอกาสที่เหตุการณ์ที่สนใจจะเกิดขึ้น. ทฤษฏีความน่าจะเป็น พิจารณาเหตุการณ์ ในบริบทของผลลัพธ์ต่าง ๆ (outcomes) ทั้งหมดทุกแบบที่อาจเกิดขึ้นได้.
เซตของผลลัพธ์แบบต่าง ๆ ที่เป็นไปได้ทั้งหมด จะเรียกว่า ปริภูมิตัวอย่าง (sample space). เหตุการณ์ (event) คือเซตย่อยของปริภูมิตัวอย่าง หรือกล่าวง่าย ๆ เหตุการณ์ คือ กลุ่มของผลลัพธ์ที่เป็นไปได้ (ผลลัพธ์ทีี่กล่าว คือผลลัพธ์ในเรื่องที่สนใจ).
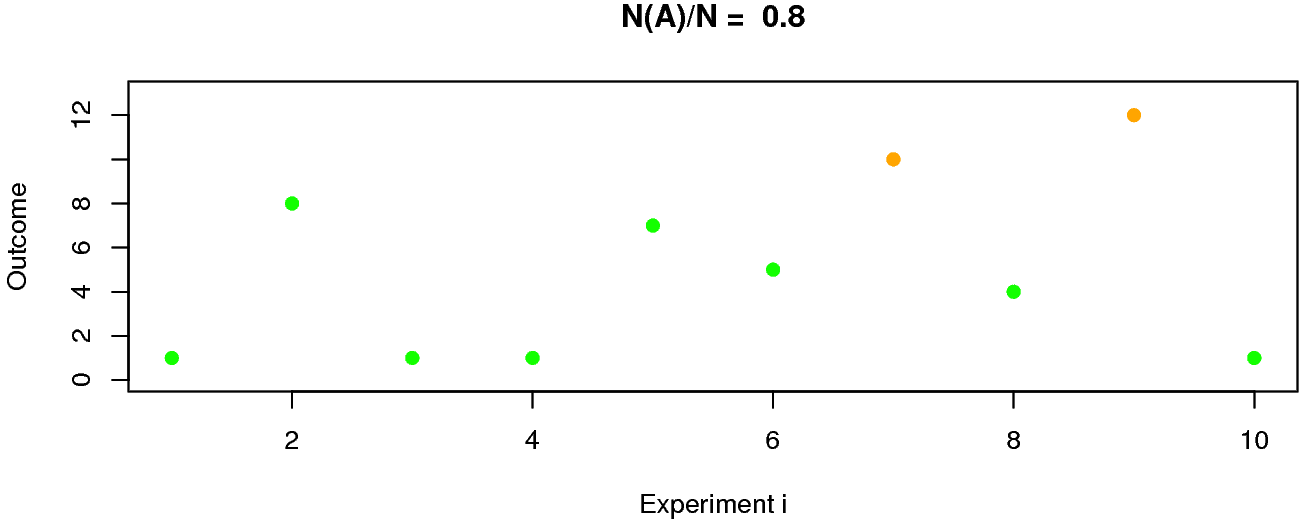
ความน่าจะเป็น อาจอธิบายง่าย ๆ จากตัวอย่าง 5 หากสมมติว่า การทดลองทำซ้ำ ๆ เป็นจำนวน \(N\) ครั้ง โดยให้สภาพแวดล้อมเหมือนเดิมมากที่สุด. กำหนดให้ \(A\) เป็นเหตุการณ์ที่สนใจ โดย \(A\) อาจจะเกิดขึ้นหรือไม่เกิดก็ได้ ในแต่ละซ้ำ. หากสิ่งที่พบคือ เมื่อจำนวนทำซ้ำ \(N\) ใหญ่ขึ้น อัตราส่วนของจำนวนครั้งที่จะเกิด \(A\) ในแต่ละซ้ำ จะมีค่าเข้าใกล้ค่า ๆ หนึ่งมากขึ้น. ค่าที่อัตราส่วนเข้าใกล้มากขึ้นเมื่อจำนวนซ้ำมากขึ้น คือค่าความน่าจะเป็นของ \(A\).
ขยายความคือ หากกำหนดให้ \(N(A)\) แทนจำนวนครั้งที่จะเกิดเหตุการณ์ \(A\) ในการทำซ้ำทั้งหมด \(N\) ครั้ง อัตราส่วน \(\frac{N(A)}{N}\) จะค่อย ๆ ลู่เข้าสู่ค่าค่าหนึ่ง เมื่อ \(N\) เพิ่มขึ้น. ค่าที่อัตราส่วนลู่เข้า จะเรียกว่า ความน่าจะเป็นที่เหตุการณ์ \(A\) จะเกิดขึ้น. ค่าความน่าจะเป็นของเหตุการณ์ \(A\) แทนด้วยสัญลักษณ์ \(\mathrm{Pr}(A)\) และความน่าจะเป็นจะมีค่าอยู่ระหว่าง \(0\) กับ \(1\). นั่นคือ \(\mathrm{Pr}(A) \in [0,1]\) โดย \(0\) หมายถึงเหตุการณ์นั้นไม่มีโอกาสเกิดขึ้นเลย และ \(1\) หมายถึงเหตุการณ์นั้นเกิดขึ้นอย่างแน่นอน.
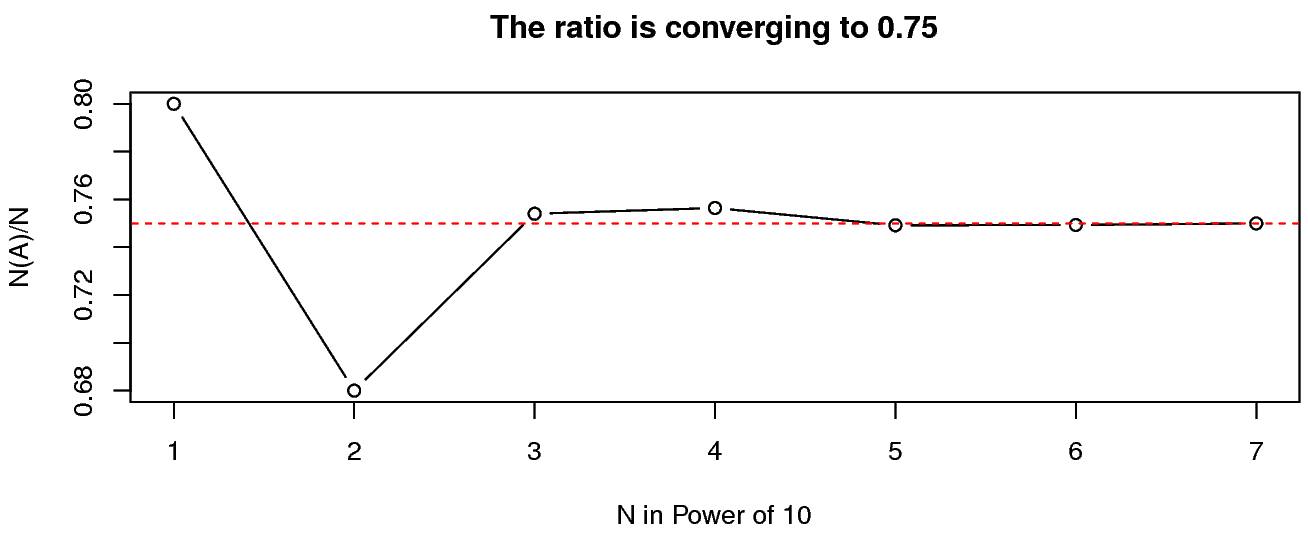
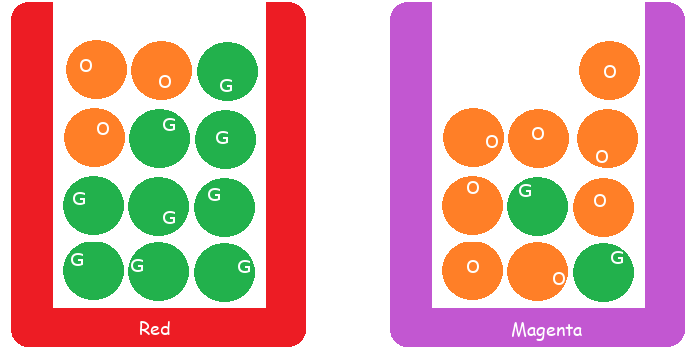
ตัวอย่างเช่น ลังใส่ลูกบอลสีต่าง ๆ ดังแสดงในรูป 1.4 หากสุ่มหยิบลูกบอล ออกมาจากลัง \(1\) ลูก และกำหนดให้ \(A\) เป็นเหตุการณ์ที่หยิบได้ลูกบอลสีเขียว. สมมติทำการทดลอง(สุ่มหยิบ)ซ้ำ \(N = 10\) ผลการจำลองเหตุการณ์ (simulation) ดังแสดงในรูป 1.5 ซึ่งบอกได้ว่า อัตราส่วนที่หยิบได้ลูกบอลสีเขียว เป็น \(\frac{N(A)}{N} = \frac{8}{10} = 0.8\). หากเพิ่มจำนวนการทำซ้ำ \(N\) จาก \(10\) เป็น \(100\) แล้วเพิ่มเป็น \(1000\) แล้วเป็น \(10000\) แล้วทำต่อ ๆ ไป จะเริ่มเห็นว่าอัตราส่วน \(\frac{N(A)}{N}\) ลู่เข้าสู่ค่าค่าหนึ่ง ดังแสดงในตาราง 1.2. เมื่อนำค่าต่าง ๆ ไปวาดกราฟ จะได้ดังรูป 1.6 ซึ่งจะเห็นว่าค่าที่ อัตราส่วน \(\frac{N(A)}{N}\) ลู่เข้าหาคือ \(0.75\). นั่นคือ ความน่าจะเป็นของการสุ่มหยิบได้ลูกสีเขียว \(\mathrm{Pr}(A) = 0.75\). มองจากอีกมุมหนึ่ง ในลังมีลูกบอล \(12\) ลูก และเป็นลูกสีเขียวอยู่ \(9\) ลุูก หากสุ่มหยิบอย่างยุติธรรม (แต่ละลูกมีโอกาสถูกหยิบเท่า ๆ กัน) โอกาสที่จะหยิบได้ลูกเขียวจะเป็น \(\frac{9}{12} = 0.75\) ซึ่งค่าที่คำนวณนี้สอดคล้องกับค่าความน่าจะเป็นที่ได้จากผลการจำลองเหตุการณ์ข้างต้น.
2.2.2.0.1 มุมมองของความน่าจะเป็น.
เหตุการณ์อาจมองได้ในหลาย ๆ ระดับ เช่น เหตุการณ์ระดับล่าง ได้แก่ เหตุการณ์ที่หยิบได้ลูกบอลลูกที่หนึ่ง \(a_1\) (ซึ่งเป็นสีเขียว) ไปจนถึง เหตุการณ์ที่หยิบได้ลูกบอลลูกที่สิบสอง \(a_{12}\) (ซึ่งเป็นสีส้ม) หรือเหตุการณ์ระดับที่สูงขึ้น ได้แก่ เหตุการณ์ที่หยิบได้ลูกบอลสีเขียว \(A\) เหตุการณ์ที่หยิบได้ลูกบอลสีส้ม \(B\) เป็นต้น. ทฤษฎีความน่าจะเป็นมองเซตจากมุมมองที่ต่างออกไป ดังแสดงในตาราง 1.1.
| สัญญลักษณ์ทั่วไป | ภาษาเฉพาะในเรื่องเซต | ภาษาเฉพาะในเรื่องความน่าจะเป็น |
|---|---|---|
| \(\Omega\) | กลุ่มของค่าที่เป็นไปได้ทั้งหมด | ปริภูมิตัวอย่าง หรือผลลัพธ์ทั้งหมดที่เป็นไปได้ |
| \(a \in \Omega\) | ค่าหนึ่งที่เป็นไปได้ | รูปแบบของผลลัพธ์ของเรื่องที่สนใจ หรือเหตุการณ์พื้นฐาน |
| \(A \subset \Omega\) | เซตย่อยของ \(\Omega\) | เหตุการณ์ที่ผลลัพธ์ใน \(A\) เกิดขึ้น |
| \(A^c\) | ส่วนเติมเต็มของ \(A\) | เหตุการณ์ที่ ผลลัพธ์ใน \(A\) ไม่เกิด |
| \(A \cap B\) | อินเตอร์เซกชัน | เหตุการณ์ที่มีผลลัพธ์ทั้งใน \(A\) และ \(B\) เกิดขึ้น |
| \(A \cup B\) | ยูเนียน | เหตุการณ์ที่มีผลลัพธ์ใน \(A\) หรือ \(B\) หรือในทั้งคู่เกิดขึ้น |
| \(A \setminus B\) | ผลต่าง | เหตุการณ์ที่ผลลัพธ์ใน \(A\) เกิดขึ้น แต่ผลลัพธ์ใน \(B\) ไม่เกิด |
| \(\emptyset\) | เซตว่าง | เหตุการณ์ที่เป็นไปไม่ได้ |
[tbl: prob set jargon]

| \(N\) | \(10\) | \(100\) | \(1000\) | \(10^4\) | \(10^5\) | \(10^6\) | \(10^7\) |
|---|---|---|---|---|---|---|---|
| \(\frac{N(A)}{N}\) | \(0.8\) | \(0.68\) | \(0.754\) | \(0.7564\) | \(0.74917\) | \(0.749291\) | \(0.7499472\) |
[tbl: prob demo N(A)/N]
 |
 |
| (a) | (b) |
2.2.2.0.2 คุณสมบัติของความน่าจะเป็น.
ความน่าจะเป็นมีคุณสมบัติที่น่าสนใจหลายอย่าง เช่น ความน่าจะเป็นที่จะเกิดผลลัพธ์จากกลุ่มผลลัพธ์ทั้งหมดทุกแบบที่เป็นไปได้ คือ ต้องพบแน่นอน ความน่าจะเป็นมีค่าสูงสุด. นั่นคือ \(\mathrm{Pr}(\Omega) = 1\). ความน่าจะเป็นที่จะพบเหตุการณ์ที่เป็นไปไม่ได้ คือ ต้องไม่พบแน่นอน ความน่าจะเป็นมีค่าต่ำสุด. นั่นคือ \(\mathrm{Pr}(\emptyset) = 0\). สัมพันธ์ด้านความน่าจะเป็นของเหตุการณ์ \(A\) กับ \(A^c\) คือ \(\mathrm{Pr}(A) = 1 - p(A^c)\) และ \(\mathrm{Pr}(A \cup A^c) = 1\) และ \(\mathrm{Pr}(A \cap A^c) = 0\). ความน่าจะเป็นของยูเนียน คือ \(\mathrm{Pr}(A \cup B) = \mathrm{Pr}(A \setminus B) + \mathrm{Pr}(B \setminus A) + \mathrm{Pr}(A \cap B)\) หรือ \(\mathrm{Pr}(A \cup B) = \mathrm{Pr}(A) + \mathrm{Pr}(B) - \mathrm{Pr}(A \cap B)\). ความน่าจะเป็นของผลต่าง คือ \(\mathrm{Pr}(A \setminus B) = \mathrm{Pr}(A) - \mathrm{Pr}(A \cap B)\).
2.2.2.0.3 เหตุการณ์ที่ไม่มีส่วนร่วมกัน.
ถ้า \(A \cap B = \emptyset\) แล้วจะเรียกว่า เหตุการณ์ \(A\) และเหตุการณ์ \(B\) ไม่มีส่วนร่วมกัน (disjoint) และยูเนียนของเหตุการณ์ที่ไม่มีส่วนร่วมกัน จะมีความน่าจะเป็น \(\mathrm{Pr}(A \cup B) = \mathrm{Pr}(A) + \mathrm{Pr}(B)\).
2.2.2.0.4 กฎของการรวมความน่าจะเป็น.
ถ้า \(B_1 \cup B_2 \cup \ldots \cup B_n = \Omega\) และ \(B_i \cap B_j = \emptyset\) สำหรับทุกๆค่าของ \(i \neq j\) ตั้งแต่ \(1, \ldots, n\) แล้ว กฎของความน่าจะเป็นรวม (law of total probability) กล่าวว่า \[\begin{eqnarray} \mathrm{Pr}(A) = \sum_{i=1}^n \mathrm{Pr}(A \cap B_i) \label{eq: prob law of total prob} \end{eqnarray}\] จากกฎของความน่าจะเป็นรวม กรณีพิเศษ คือ \(\mathrm{Pr}(A) = \mathrm{Pr}(A \cap B) + \mathrm{Pr}(A \cap B^c)\).
2.2.2.0.5 ตัวแปรสุ่ม.
เพื่อความสะดวก เหตุการณ์อาจถูกระบุด้วย ตัวแปรสุ่ม เช่น จากตัวอย่าง เหตุการณ์ที่หยิบได้ลูกบอลสีเขียว และเหตุการณ์ที่หยิบได้ลูกบอลสีส้ม จะสามารถถูกอ้างถึงได้สะดวก และชัดเจนกว่า ถ้ากำหนด ตัวแปรสุ่ม \(B\) แทนสีของลูกบอลที่ถูกสุ่มหยิบขึ้นมา. เหตุการณ์ที่หยิบได้ลูกบอลสีเขียว สามารถ เขียนเป็น \(B = 0\) เมื่อ \(0\) แทนสีเขียว และ เหตุการณ์ที่หยิบได้ลูกบอลสีส้ม สามารถ เขียนเป็น \(B = 1\) เมื่อ \(1\) แทนสีส้ม. ตัวแปรสุ่ม (random variable) อาจถูกนิยามว่า เป็นตัวแปรที่ค่าของมันขึ้นกับผลลัพธ์ของเรื่องที่สนใจ เมื่อเรื่องที่สนใจเป็นกระบวนการที่มีความไม่แน่นอนอยู่.
หมายเหตุ ตัวแปรสุ่มเป็นการแทนเหตุการณ์ด้วยค่าตัวเลข โดยสำหรับธรรมชาติของเหตุการณ์ที่ไม่ได้เป็นตัวเลข การใช้งานตัวแปรสุ่มนี้อาจทำได้โดยการกำหนดความหมายให้กับตัวเลข เช่น \(0\) แทนสีเขียว และ \(1\) แทนสีส้ม. แต่หลาย ๆ ครั้งเพื่อความสะดวกและชัดเจน อาจมีการใช้สัญลักษณ์ เช่น \(\mbox{`g'}\) แทนตัวเลข \(0\) ในกรณีที่ระบุถึงสีเขียว.
ฟังก์ชันการแจกแจง (distribution function) ของตัวแปรสุ่ม \(X\) คือฟังก์ชัน \(F: \mathbb{R} \rightarrow [0,1]\) โดย \(F(x) = \mathrm{Pr}(X \leq x)\).
ตัวแปรสุ่มอาจมีได้หลายแบบขึ้นกับลักษณะของค่าของมัน ซึ่งค่าของมันก็คือลักษณะของผลลัพธ์ที่เป็นไปได้. ตัวแปรสุ่มวิยุต (discrete random variable) คือตัวแปรสุ่มที่ค่าของมัน อยู่ในเซตจำกัด (finite set) หรืออยู่ในเซตไม่จำกัดแต่นับได้ (countably infinite set). ตัวอย่าง ตัวแปรสุ่มสีของลูกบอล \(B\) นี้เป็นตัวแปรสุ่มวิยุต เนื่องจากค่าของมันมาจากเซตจำกัด ได้แก่ \(\{0, 1\}\) (มีจำนวนสมาชิกน้อยกว่าค่าอนันต์ \(\infty\)). ตัวแปรสุ่มจำนวนต้นทุเรียน ก็เป็นตัวแปรสุ่มวิยุต เนื่องจากค่าของมันมาจากเซตไม่จำกัดแต่นับได้ ได้แก่ \(\{0, 1, 2, 3, \ldots \}\). แต่ตัวแปรสุ่มปริมาณน้ำในอ่างเก็บน้ำ ไม่ใช่ตัวแปรสุ่มวิยุต เพราะว่า ค่าของมันมาจาก \(\mathbb{R}^+\) ตัวแปรสุ่มปริมาณน้ำในอ่างเก็บน้ำ จะเป็นตัวแปรสุ่มต่อเนื่อง. หัวข้อ 1.2.4 อภิปรายตัวแปรสุ่มต่อเนื่องเพิ่มเติม.
ตัวแปรสุ่มวิยุต \(X\) จะมีฟังก์ชันมวลความน่าจะเป็น (probability mass function คำย่อ pmf) \(f: \mathbb{R} \rightarrow [0,1]\) โดย \(f(x) = \mathrm{Pr}(X = x)\).
ค่าคาดหมาย (expectation หรือ expected value) เป็นค่าเฉลี่ยของตัวแปรสุ่ม และใช้สัญกรณ์ เช่น \(E[X]\) สำหรับค่าคาดหมายของตัวแปรสุ่ม \(X\). โดยสำหรับตัวแปรสุ่มวิยุตที่เป็นตัวเลข ค่าคาดหมายสามารถคำนวณได้จาก \[\begin{eqnarray} E[X] &=& \sum_x x \cdot \mathrm{Pr}(X=x) \label{eq: prob expectation}. \end{eqnarray}\]
ความแปรปรวน (variance) ของตัวแปรสุ่ม ใช้สัญกรณ์ เช่น \(\mathrm{var}[X]\) ซึ่งค่าความแปรปรวน คำนวณได้จาก \[\begin{eqnarray} \mathrm{var}[X] &=& E[(X -E[X])^2] \label{eq: prob variance} \end{eqnarray}\]
2.2.2.0.6 ความน่าจะเป็นร่วม.
เมื่อใช้ตัวแปรสุ่มอธิบายเหตุการณ์ ในกรณีที่สนใจเหตุการณ์ที่เกี่ยวข้องกับตัวแปรสุ่มตั้งแต่สองตัวขึ้นไป ความน่าจะเป็นที่ใช้ จะเรียกว่า ความน่าจะเป็นร่วม (joint probability) และใช้สัญกรณ์ เช่น \(\mathrm{Pr}(X, Y)\) หรือความน่าจะเป็นร่วมของตัวแปรสุ่ม \(X\) และตัวแปรสุ่ม \(Y\) และความน่าจะเป็นร่วม \(\mathrm{Pr}(X, Y) = \mathrm{Pr}(X \cap Y)\). นั่นคือ \(\mathrm{Pr}(X = x, Y = y)\) หมายถึง ความน่าจะเป็นที่ ตัวแปรสุ่ม \(X\) จะมีค่าเป็น \(x\) และตัวแปรสุ่ม \(Y\) จะมีค่าเป็น \(y\).
ความแปรปรวนร่วมเกี่ยว (covariance) ของตัวแปรสุ่มสองตัว ใช้สัญกรณ์ เช่น \(\mathrm{cov}[X, Y]\) ซึ่งค่าความแปรปรวนร่วมเกี่ยว คำนวณได้จาก \[\begin{eqnarray} \mathrm{cov}[X, Y] &=& E_{X,Y}[(X - E[X])(Y - E[Y])] \nonumber \\ &=& E_{X,Y}[XY] - E[X]E[Y] \label{eq: prob covariance} \end{eqnarray}\] เมื่อ \(E_{X,Y}\) หมายถึงค่าคาดหมาย ที่คิดโดยคำนึงถึงความน่าจะเป็นร่วมของ \(X\) และ \(Y\). นั่นคือ สำหรับตัวแปรสุ่มวิยุต \(\mathrm{cov}[X, Y] = \sum_x \sum_y (x - E[X])(y - E[Y]) \cdot \mathrm{Pr}(X=x, Y=y)\).
2.2.3 ความน่าจะเป็นแบบมีเงื่อนไข
ความน่าจะเป็นแบบมีเงื่อนไข (conditional probability) ประมาณโอกาสที่จะเกิดเหตุการณ์ที่สนใจ ในกรณีที่รู้ผลลัพธ์ของเงื่อนไข. ความน่าจะเป็นแบบมีเงื่อนไขจะเน้นบริบทของเงื่อนไข. สัญกรณ์ เช่น \(\mathrm{Pr}(A|B)\) แทนความน่าจะเป็นแบบมีเงื่อนไข ที่หมายถึง ความน่าจะเป็นของเหตุการณ์ \(A\) ในกรณีที่เหตุการณ์ \(B\) เป็นจริง. เหตุการณ์ \(B\) เป็นเงื่อนไข และเป็นบริบทเสริม เป็นข้อมูลเสริมในการประมาณความน่าจะเป็น.
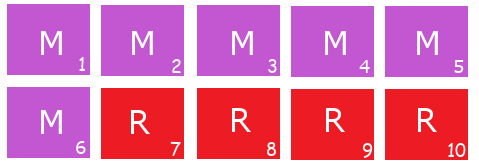
จากตัวอย่างของรูป 1.4 พิจารณาตัวอย่างที่คราวนี้ มีลังอยู่ \(10\) ลัง ซึ่ง เป็นลังสีแดง \(4\) ลัง และเป็นลังสีบานเย็น \(6\) ลัง ดังรูป 1.8. ถ้าสุ่มยกมาหนึ่งลัง โอกาสที่จะเป็นลังที่ 7 คือ \(1/10\) แต่ถ้าเห็นว่าลังที่สุ่มมาเป็นสีแดง โอกาสที่จะเป็นลังที่ 7 คือ \(1/4\) เพราะว่า มีแค่ลังที่ 7 ถึงลังที่ 10 ที่เป็นสีแดงอยู่แค่ \(4\) ลัง. ถ้าเห็นว่าลังที่สุ่มมาสีบานเย็น โอกาสที่จะเป็นลังที่ 7 ไม่มีเลย หรือโอกาสเป็น \(0\) เพราะลังที่ 7 สีแดง. ข้อมูลพิเศษ หรือบริบทเพิ่มเติมนี้ คือเงื่อนไขที่ใช้ประกอบการประมาณโอกาสของเหตุการณ์.
2.2.3.0.1 การคำนวณ.
ความน่าจะเป็นแบบมีเงื่อนไข สามารถคำนวณได้จาก \[\begin{eqnarray} \mathrm{Pr}(A|B) = \frac{\mathrm{Pr}(A \cap B)}{\mathrm{Pr}(B)} \label{eq: prob cond prob relation} \end{eqnarray}\] เมื่อ \(\mathrm{Pr}(B) > 0\). จากสมการ \(\eqref{eq: prob cond prob relation}\) จะได้ \[\begin{eqnarray} \mathrm{Pr}(X, Y) = \mathrm{Pr}(X|Y) \cdot \mathrm{Pr}(Y) \label{eq: prob product rule} \end{eqnarray}\] เมื่อ \(X\) และ \(Y\) คือตัวแปรสุ่ม. สมการ \(\eqref{eq: prob product rule}\) มักเรียกว่า กฎผลคูณ (product rule). นอกจากนั้น พิจารณาสมการ \(\eqref{eq: prob law of total prob}\) และ \(\eqref{eq: prob product rule}\) จะพบว่า \[\begin{eqnarray} \mathrm{Pr}(X) = \sum_y \mathrm{Pr}(X, Y=y) = \sum_y \mathrm{Pr}(X|Y = y) \cdot \mathrm{Pr}(Y = y) \label{eq: prob sum rule} \end{eqnarray}\] ซึ่ง สมการนี้มักเรียกว่า กฎผลรวม (sum rule). สังเกตว่า การใช้กฎผลรวม จะลดตัวแปรสุ่มลงไป ซึ่งการทำเช่นนี้ จึงอาจถูกเรียกว่า การสลายปัจจัย (marginalization).
กฎผลคูณสามารถใช้ต่อเนื่องกัน ในลักษณะลูกโซ่ \[\begin{eqnarray} \mathrm{Pr}(X_1, X_2, \ldots, X_n) &=& \mathrm{Pr}(X_1) \cdot \mathrm{Pr}(X_2, \ldots, X_n|X_1) \nonumber \\ &=& \mathrm{Pr}(X_1) \cdot \mathrm{Pr}(X_2|X_1) \cdot \mathrm{Pr}(X_3, \ldots, X_n|X_1, X_2) \nonumber \\ &\vdots& \nonumber \\ &=& \mathrm{Pr}(X_1) \cdot \mathrm{Pr}(X_2|X_1) \cdot \mathrm{Pr}(X_3|X_1, X_2) \cdot \mathrm{Pr}(X_4|X_1, X_2, X_3) \cdot \cdots \nonumber \\ &\;& \; \cdots \mathrm{Pr}(X_n|X_1, \ldots, X_{n-1}) \label{eq: prob chain rule} \end{eqnarray}\] ซึ่งสมการ \(\eqref{eq: prob chain rule}\) มักจะถูกเรียกว่า กฎลูกโซ่ของความน่าจะเป็น (chain rule of probability).
กฎของเบส์ (Bayes’ rule หรือ Bayes’ theorem) คือ \[\begin{eqnarray} \mathrm{Pr}(Y|X) &=& \frac{\mathrm{Pr}(X|Y) \cdot \mathrm{Pr}(Y)}{\mathrm{Pr}(X)} \label{eq: prob Bayes' 1} \\ &=& \frac{\mathrm{Pr}(X|Y) \cdot \mathrm{Pr}(Y)}{\sum_y \mathrm{Pr}(X|Y=y) \cdot \mathrm{Pr}(Y=y)} \label{eq: prob Bayes' 2} \end{eqnarray}\] จากความสัมพันธ์ที่ได้จากกฎของเบส์ การอนุมานค่าที่สนใจจากข้อมูล มักจะเรียกชื่อพจน์ต่าง ๆ ในสมการ \(\eqref{eq: prob Bayes' 1}\) เพื่อความสะดวก ดังนี้ ถ้ากำหนดให้ตัวแปรสุ่ม \(Y\) แทนเป้าหมายของการอนุมาน และตัวแปรสุ่ม \(X\) แทนข้อมูลประกอบ แล้ว \(\mathrm{Pr}(Y)\) จะเรียกว่า ความน่าจะเป็นก่อน (prior probability คำย่อ prior) ซึ่งหมายถึง ก่อนการนำข้อมูลประกอบมาคิด \(\mathrm{Pr}(Y|X)\) จะเรียกว่า ความน่าจะเป็นภายหลัง (posterior probability คำย่อ posterior) ซึ่งหมายถึง ภายหลังการนำข้อมูลประกอบมาคิด และ หาก \(\mathrm{Pr}(X|Y)\) เขียนอยู่ในรูปฟังก์ชัน \(f(y) = \mathrm{Pr}(X|Y=y)\) ก็จะถูกเรียกว่า ฟังก์ชันควรจะเป็น (likelihood function คำย่อ likelihood). ดังนั้น จากกฎของเบส์ และชื่อพจน์ต่าง ๆ อาจสรุปความสัมพันธ์ได้เป็น \(\mathrm{posterior} \propto \mathrm{likelihood} \cdot \mathrm{prior}\).
2.2.3.0.2 ตัวอย่างการคำนวณ.
กลับมาที่รูป 1.8 อีกครั้ง คราวนี้จะสุ่มเลือกลัง และพอได้ลังแล้วก็จะสุ่มหยิบลูกบอลออกมา. โอกาสที่จะสุ่มได้ลังแดงเป็น \(\frac{4}{10}\) หรือความน่าจะเป็นที่จะได้ลังสีแดง \(\mathrm{Pr}(C = \mbox{`r'}) = 0.4\) โดย \(C = \mbox{`r'}\) แทนเหตุการณ์ที่จะได้ลังสีแดง. ในทำนองเดียวกัน ความน่าจะเป็นที่จะได้ลังสีบานเย็น \(\mathrm{Pr}(C = \mbox{`m'}) = 0.6\).
ถ้ารู้ว่าเป็นลังสีแดง เมื่อสุ่มหยิบลูกบอลมา โอกาสที่จะหยิบได้ลูกบอลสีเขียว คือ \(\frac{9}{12} = 0.75\) หรือเขียนเป็นสัญกรณ์ ได้ว่า \(\mathrm{Pr}(B = \mbox{`g'}|C = \mbox{`r'}) = 0.75\) โดย \(B = \mbox{`g'}\) แทนเหตุการณ์ที่จะหยิบได้ลูกบอลสีเขียว. ทำนองเดียวกัน ก็จะได้ความน่าจะเป็นแบบมีเงื่อนไขอื่น ๆ ดังนี้
\(\mathrm{Pr}(B = \mbox{`o'}|C = \mbox{`r'}) = 0.25\),
\(\mathrm{Pr}(B = \mbox{`g'}|C = \mbox{`m'}) = 0.20\),
\(\mathrm{Pr}(B = \mbox{`o'}|C = \mbox{`m'}) = 0.80\). \(\square\)
สังเกตว่า ความน่าจะเป็นที่จะหยิบได้ลูกบอลสีเขียวเมื่อรู้ว่าลังสีแดง \(\mathrm{Pr}(B = \mbox{`g'}|C = \mbox{`r'})\) ไม่เหมือนกับความน่าจะเป็นที่จะหยิบลูกบอลสีเขียวและสุ่มได้ลังสีแดง \(\mathrm{Pr}(B = \mbox{`g'}, C = \mbox{`r'})\). สำหรับ \(\mathrm{Pr}(B = \mbox{`g'}|C = \mbox{`r'}) = 0.75\) นั้นไม่ต้องสนใจเลยว่าโอกาสที่จะได้ลังสีแดงเป็นเท่าไร. ในขณะที่ \(\mathrm{Pr}(B = \mbox{`g'}, C = \mbox{`r'})\) จะประกอบด้วยโอกาสที่จะได้ลังสีแดง \(\mathrm{Pr}(C = \mbox{`r'}) = 0.4\) และโอกาสที่จะหยิบได้ลูกบอลสีเขียวจากลังนั้น \(\mathrm{Pr}(B = \mbox{`g'}|C = \mbox{`r'}) = 0.75\) ซึ่งจากกฎผลคูณ (สมการ \(\eqref{eq: prob product rule}\)) จะได้ \[\begin{eqnarray} \mathrm{Pr}(B = \mbox{`g'}, C = \mbox{`r'}) &=& \mathrm{Pr}(C = \mbox{`r'}) \cdot \mathrm{Pr}(B = \mbox{`g'}|C = \mbox{`r'}) \nonumber \\ &=& (0.4) \cdot (0.75) = 0.3 \nonumber . \end{eqnarray}\]
ในทำนองเดียวกันก็จะได้ค่าความน่าจะเป็นต่าง ๆ ดังแสดงในตาราง 1.3.
ทบทวน (1) ผลรวมของความน่าจะเป็นของทุก ๆ เหตุการณ์เป็น \(1\). นั่นคือ \[\begin{eqnarray} \mathrm{Pr}(\Omega) &=& \mathrm{Pr}(C = \mbox{`r'}, B = \mbox{`g'}) + \mathrm{Pr}(C = \mbox{`r'}, B = \mbox{`o'}) \nonumber \\ &\;& + \mathrm{Pr}(C = \mbox{`b'}, B = \mbox{`g'}) + \mathbb{P}(C = \mbox{`b'}, B = \mbox{`o'}) \nonumber \\ &=& 0.3 + 0.1 + 0.12 + 0.48 = 1 \nonumber . \end{eqnarray}\] ธรรมชาตินี้เป็นคุณสมบัติพื้นฐานของความน่าจะเป็น. ทบทวน (2) ความน่าจะเป็นของเหตุการณ์ \(X\) เท่ากับผลรวมของความน่าจะเป็นของเหตุการณ์ \(X\) และ \(Y\) สำหรับทุก ๆ ความเป็นไปได้ของ \(Y\) ดังเช่น \[\begin{eqnarray} \mathrm{Pr}(C = \mbox{`r'}) &=& \mathrm{Pr}(C = \mbox{`r'}, B = \mbox{`g'}) + \mathrm{Pr}(C = \mbox{`r'}, B = \mbox{`o'}) \nonumber \\ &=& 0.3 + 0.1 = 0.4 \nonumber \\ \mathrm{Pr}(C = \mbox{`m'}) &=& \mathrm{Pr}(C = \mbox{`m'}, B = \mbox{`g'}) + \mathrm{Pr}(C = \mbox{`m'}, B = \mbox{`o'}) \nonumber \\ &=& 0.12 + 0.48 = 0.6 \nonumber . \end{eqnarray}\] ธรรมชาตินี้คือกฎผลบวก (สมการ \(\eqref{eq: prob sum rule}\)).
จากกฎของการบวก จะได้ ความน่าจะเป็นที่จะหยิบได้ลูกบอลสีเขียว และสีส้ม (โดยไม่สนใจสีของลัง) \[\begin{eqnarray} \mathrm{Pr}(B = \mbox{`g'}) &=& \mathrm{Pr}(C = \mbox{`r'}, B = \mbox{`g'}) + \mathrm{Pr}(C = \mbox{`m'}, B = \mbox{`g'}) \nonumber \\ &=& 0.3 + 0.12 = 0.42 \nonumber \\ \mathrm{Pr}(B = \mbox{`o'}) &=& \mathrm{Pr}(C = \mbox{`r'}, B = \mbox{`o'}) + \mathrm{Pr}(C = \mbox{`m'}, B = \mbox{`o'}) \nonumber \\ &=& 0.1 + 0.48 = 0.58 \nonumber . \end{eqnarray}\] และความน่าจะเป็นของลังถ้าหากรู้สีของลูกบอลที่สุ่มหยิบออกมาหนึ่งลูก \[\begin{eqnarray} \mathrm{Pr}(C = \mbox{`r'}|B = \mbox{`g'}) &=& \frac{\mathrm{Pr}(B = \mbox{`g'}|C = \mbox{`r'}) \cdot \mathrm{Pr}(C = `r')}{\mathrm{Pr}(B = \mbox{`g'})} \nonumber \\ &=& \frac{(0.75) (0.4)}{0.42} = 0.71 \nonumber . \end{eqnarray}\] ความน่าจะเป็นแบบมีเงื่อนไข และทฤษฎีของเบส์ ช่วยให้สามารถหาค่าความน่าจะเป็นที่สนใจได้ จากค่าของความน่าจะเป็นอื่นที่ประเมินความน่าจะเป็นได้ง่ายกว่า เช่น \(\mathrm{Pr}(B|C)\) จะประเมินได้ง่าย เพราะว่า ลูกบอลอยู่ในลัง ดังนั้นจะนับได้ง่ายว่า ในลังแต่ละสี มีลูกบอลสีไหนจำนวนเท่าไร ต่อจำนวนลูกบอลทั้งหมดในลัง. \(\mathrm{Pr}(C)\) ก็ประเมินได้ง่าย แต่ \(\mathrm{Pr}(C|B)\) ประเมินตรง ๆ ได้ยาก เพราะลูกบอลแต่สีกระจายไปทุก ๆ ลัง.
| ลัง | ลูกบอล \(B\) | |
| \(C\) | เขียว ‘g’ | ส้ม ‘o’ |
| แดง ‘r’ | 0.3 | 0.1 |
| บานเย็น ‘m’ | 0.12 | 0.48 |
[tbl: prob cond prob table]
2.2.3.0.3 การตีความและความสับสนที่พบได้บ่อย.
เพื่อหาความน่าจะเป็นที่จะได้ลูกบอลสีเขียว \(\mathrm{Pr}(B = \mbox{`g'})\) บ่อยครั้งมักถูกคำนวณด้วย \(11/22 = 0.5\) ซึ่งได้จากการนับลูกบอลสีเขียว เทียบกับลูกบอลทั้งหมด. กรณีนี้ ค่าที่ถูกต้อง \(\mathrm{Pr}(B = \mbox{`g'}) = 0.42\) ไม่เท่ากับ \(11/22 = 0.5\) ซึ่ง \(11/22\) ได้จากการนับลูกบอล โดยเสมือนว่าไม่มีลัง. กรณีหลังนั้น คือสถานการณ์ที่เทลูกบอลทั้งหมดออกจากลัง และสุ่มหยิบลูกไหนก็ได้. ในขณะที่ตัวอย่างนี้ ต้องเลือกลังก่อน ถ้าเลือกลังแล้ว ต้องสุ่มหยิบลูกจากในลังที่เลือก.
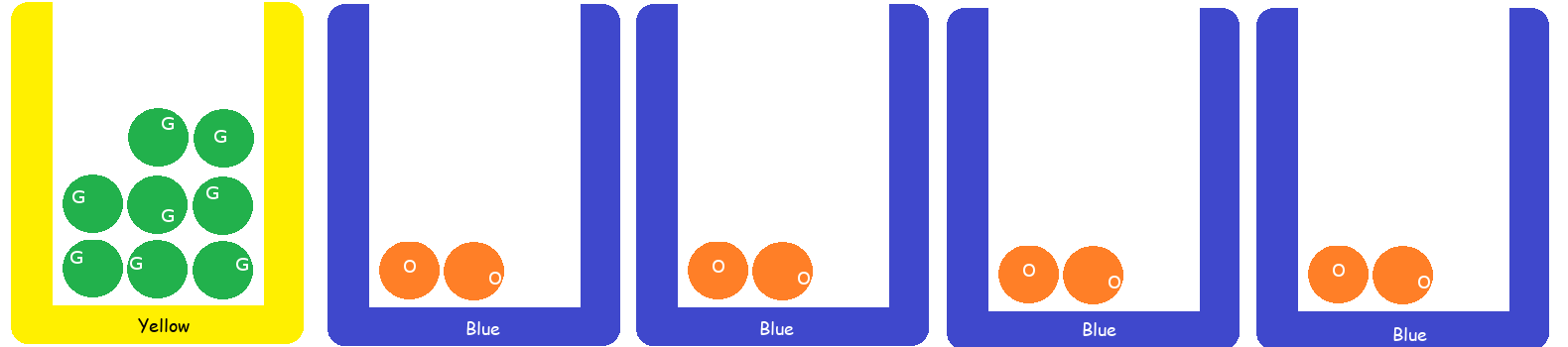
สองกรณีนี้ จะเห็นต่างกันชัดเจนมาก ถ้าพิจารณากรณี เช่น ตัวอย่างในรูป 1.9 มีลังสีเหลืองแค่ \(1\) ลัง มีลังสีฟ้า \(4\) ลัง แต่ลังสีเหลืองมีลูกบอล \(8\) ลูก ที่ทั้งหมดสีเขียว และลังสีฟ้ามีลูกบอล \(2\) ลูก ที่ทั้งหมดสีส้ม. เมื่อคิดความน่าจะเป็นแล้วจะพบว่า กรณีนี้ ถ้าเทลูกบอลทั้งหมดออกจากลัง แล้วสุ่มหยิบโอกาสที่จะได้สีเขียวเป็น \(8/16 = 1/2\) แต่ถ้าสุ่มเลือกลังก่อน ลังสีเหลืองมีโอกาสแค่ \(1/5\) แล้วโอกาสได้ลูกบอลสีเขียวจากลังนี้เป็น \(1\) ในขณะที่โอกาสที่จะได้ลังสีฟ้าเป็น \(4/5\) แต่โอกาสได้ลูกบอลสีเขียวเป็น \(0\) ดังนั้นโอกาสได้ลูกบอลสีเขียวจะเป็นแค่ \((1/5) \cdot 1 + (4/5) \cdot 0 = 1/5\).
ภาพความเกี่ยวเนื่องของเหตุการณ์ และความน่าจะเป็นร่วม และความน่าจะเป็นแบบมีเงื่อนไข แสดงในรูป 1.10 สำหรับสองเหตุการณ์ และรูป 1.11 สำหรับสามเหตุการณ์.


2.2.3.0.4 ความเป็นอิสระต่อกัน.
เหตุการณ์ \(A\) และเหตุการณ์ \(B\) จะเป็นอิสระต่อกัน (independent) ก็ต่อเมื่อ \(\mathrm{Pr}(A \cap B) = \mathrm{Pr}(A) \cdot \mathrm{Pr}(B)\). ดังนั้น จากกฎผลคูณ \(\mathrm{Pr}(A \cap B) = \mathrm{Pr}(A|B) \cdot \mathrm{Pr}(B)\) จะได้ว่า \(\mathrm{Pr}(A|B) = \mathrm{Pr}(A)\) เมื่อ \(A\) และ \(B\) เป็นอิสระต่อกัน. ความหมายก็คือ ถ้าเหตุการณ์ \(A\) และเหตุการณ์ \(B\) เป็นอิสระต่อกันแล้ว การรู้หรือไม่รู้ข้อมูลของ \(B\) ก็ไม่ได้เปลี่ยนการประมาณค่าของ \(A\).
2.2.3.1 ตัวอย่างการใช้งานความน่าจะป็นแบบมีเงื่อนไข
2.2.3.1.1 ปัญหาการตรวจเต้านมด้วยภาพเอ็กซเรย์.
สมมติว่า ผู้หญิงอายุสี่สิบปีคนหนึ่ง ไปทำการตรวจเต้านมด้วยภาพเอ็กซเรย์ (mammogram) แล้วผลตรวจเป็นบวก (positive ซึ่งหมายถึง เครื่องตรวจบอกว่าเป็นมะเร็ง) โอกาสที่ผู้หญิงคนนี้จะเป็นมะเร็งจริง ๆ เป็นเท่าไร
สมมติว่าข้อมูลประกอบ คือ วิธีการตรวจเต้านมด้วยเอ็กซเรย์มีค่าความไว (sensitivity) ที่ \(80\%\) ซึ่งหมายความว่า ถ้าคนที่เป็นมะเร็งไปทำการตรวจแล้ว โอกาสที่จะได้ผลเป็นบวก คือ \(0.8\). นั่นคือ \(\mathrm{Pr}(M = 1|C = 1) = 0.8\) เมื่อ \(M = 1\) แทนผลตรวจเป็นบวก (ถ้า \(M = 0\) คือผลตรวจเป็นลบ) และ \(C = 1\) แทนผู้รับการตรวจเป็นมะเร็งจริง ๆ (ถ้า \(C = 0\) คือผู้รับการตรวจไม่ได้เป็นมะเร็ง).
ความเข้าใจผิดอย่างหนึ่งที่พบบ่อย คือ การสรุปว่า ผู้หญิงคนนั้นมีโอกาสเป็นมะเร็ง \(80\%\) ซึ่งผิด เพราะการสรุปนี้ ไม่ได้คำนึงถึงความน่าจะเป็นก่อน นั่นคือ โอกาสที่ผู้หญิงอายุสี่สิบปี จะเป็นมะเร็งเต้านม ซึ่งจากสถิติ 6 คือ \(17\%\). นั่นคือ \(\mathrm{Pr}(C = 1) = 0.17\).
นอกจากนั้น การสรุปยังต้องการข้อมูลว่า วิธีการตรวจมีผลบวกผิด (false positive หรือสัญญาณหลอก false alarm) เป็นเท่าไร ถ้าวิธีการตรวจมีผลบวกผิด เป็น \(10\%\). นั่นคือ \(\mathrm{Pr}(M = 1|C = 0) = 0.1\).
ดังนั้น เมื่อรวมหลักฐานทุกอย่างเข้าด้วยกัน โดยใช้กฎของเบส์ จะได้ว่า \[\begin{eqnarray} \mathrm{Pr}(C = 1|M = 1) &=& \frac{\mathrm{Pr}(M = 1|C = 1) \mathrm{Pr}(C = 1)}{\mathrm{Pr}(M = 1|C = 0) \mathrm{Pr}(C = 0) + \mathrm{Pr}(M = 1|C = 1) \mathrm{Pr}(C = 1)} \nonumber \\ &=& \frac{0.8 \cdot 0.17}{0.1 \cdot 0.83 + 0.8 \cdot 0.17} = 0.62 \nonumber . \end{eqnarray}\] ดังนั้นคำตอบที่ถูกคือ \(62\%\).
2.2.3.1.2 ปัญหามอนตี้ฮอล.
ปัญหามอนตี้ฮอล (Monty Hall Problem) เป็นสถานการณ์การตัดสินใจของผู้เข้าแข่งขันเกมส์โชว์มอนตี้ฮอล. ผู้เข้าแข่งขันต้องเลือกเปิดประตูหนึ่งในสามประตู. มีประตูหนึ่งที่ซ่อนรางวัลใหญ่ไว้. อีกสองประตูมีแต่ของปลอบใจ. ผู้เข้าแข่งขันจะได้อะไรก็ตามที่อยู่หลังประตูกลับบ้าน. แต่หลังจากผู้เข้าแข่งขันเลือกประตูไปแล้ว แทนที่พิธีกรจะเปิดประตูนั้นออกทันที. พิธีกรจะเดินไปที่ประตู และเลือกเปิดประตูหนึ่ง ที่ผู้เข้าแข่งขันไม่ได้เลือก. ประตูที่พิธีกรเปิด จะไม่มีรางวัลอยู่ และเสนอโอกาสให้ผู้เข้าแข่งขันเปลี่ยนใจ ไปเลือกประตูที่เหลืออยู่. ผู้เข้าแข่งขันควรจะเลือกยืนยันประตูเก่า หรือควรจะเลือกเปลี่ยนไปประตูใหม่
ปัญหานี้ ในมุมมองของความน่าจะเป็นแบบมีเงื่อนไข คือ การหาค่าความน่าจะเป็นที่ประตูใหม่จะมีรางวัล เปรียบเทียบกับการหาค่าความน่าจะเป็นที่ประตูเก่าจะมีรางวัล.
กำหนดให้ \(\mathrm{Pr}(R = 3|C = 1, H = 2)\) แทน การหาค่าความน่าจะเป็นที่รางวัลจะอยู่ประตูที่สาม เมื่อผู้เข้าแข่งขันเลือกประตูที่หนึ่ง และพิธีกรเปิดประตูที่สอง โดย \(R\) แทนประตูที่มีรางวัล \(C\) แทนประตูที่เลือก และ \(H\) แทนประตูที่พิธีกรเปิด.
พิจารณา กรณี \[\begin{eqnarray} \mathrm{Pr}(R = 1| C = 1, H = 2) &=& \frac{\mathrm{Pr}(R = 1, H = 2| C = 1)}{\mathrm{Pr}(H = 2| C = 1)} \label{eq: prob monty hall stay} \end{eqnarray}\] ซึ่งเป็นตัวแทนของโอกาส ในกรณีผู้เข้าแข่งขันไม่เปลี่ยนใจแล้วได้รางวัล เปรียบเทียบกับกรณี \[\begin{eqnarray} \mathrm{Pr}(R = 3| C = 1, H = 2) &=& \frac{\mathrm{Pr}(R = 3, H = 2| C = 1)}{\mathrm{Pr}(H = 2| C = 1)} \label{eq: prob monty hall change} \end{eqnarray}\] ซึ่งเป็นตัวแทนของโอาส ในกรณีผู้เข้าแข่งขันเปลี่ยนใจแล้วได้รางวัล.
เพื่อแก้สมการ \(\eqref{eq: prob monty hall stay}\) และ \(\eqref{eq: prob monty hall change}\) กฎของเบส์ ต้องการข้อมูลเพิ่มเติม. โอกาสที่รางวัลจะอยู่ประตูไหน มีเท่า ๆ กัน. นั่นคือ \(\mathrm{Pr}(R = 1) = \mathrm{Pr}(R = 2) = \mathrm{Pr}(R = 3) = 1/3\) และ เพราะประตูที่มีรางวัลเป็นอิสระกับประตูที่ผู้แข่งขันเลือก ดังนั้น \(\mathrm{Pr}(R) = \mathrm{Pr}(R|C)\). นั่นคือ \(\mathrm{Pr}(R = 1|C = 1) = \mathrm{Pr}(R = 2|C = 1) = \mathrm{Pr}(R = 3|C = 1) = 1/3\).
แต่พิธีกรต้องไม่เปิดประตูที่ผู้แข่งขันเลือก หรือไม่เปิดประตูที่มีรางวัล ดังนั้น
| \(\mathrm{Pr}(H = 2|C = 1, R = 1) = 1/2\) | เพราะ พิธีกรเลือกเปิดประตูที่สองหรือที่สามก็ได้ |
| \(\mathrm{Pr}(H = 2|C = 1, R = 2) = 0\) | เพราะ พิธีกรเปิดประตูที่มีรางวัลไม่ได้ |
| \(\mathrm{Pr}(H = 2|C = 1, R = 3) = 1\) | เพราะ พิธีกรเปิดประตูที่สองได้เท่านั้น |
จากข้อมูลประกอบเหล่านี้ อนุมานได้ว่า \[\begin{eqnarray} \mathrm{Pr}(R = 1, H = 2| C = 1) &=& \mathrm{Pr}(H =2 | C = 1, R = 1) \cdot \mathrm{Pr}(R = 1| C= 1) \nonumber \\ &=& (1/2) (1/3) = 1/6 \nonumber \\ \mathrm{Pr}(R = 2, H = 2| C = 1) &=& \mathrm{Pr}(H =2 | C = 1, R = 2) \cdot \mathrm{Pr}(R = 2| C= 1) \nonumber \\ &=& (0) (1/3) = 0 \nonumber \\ \mathrm{Pr}(R = 3, H = 2| C = 1) &=& \mathrm{Pr}(H =2 | C = 1, R = 3) \cdot \mathrm{Pr}(R = 3| C= 1) \nonumber \\ &=& (1) (1/3) = 1/3 \nonumber \end{eqnarray}\] ซึ่งเท่านี้ก็เพียงพอแล้ว จะสรุปได้ว่า โอกาสที่จะได้รางวัล ถ้าผู้แข่งขันเปลี่ยนประตู จะมากกว่า โอกาสถ้าผู้แข่งขันไม่เปลี่ยน (เพราะว่า สมการ \(\eqref{eq: prob monty hall stay}\) และ \(\eqref{eq: prob monty hall change}\) มีตัวหารเท่ากัน).
อย่างไรก็ตาม ค่า \(\mathrm{Pr}(H = 2|C = 1)\) ก็สามารถอนุมานได้จากกฎผลรวม. นั่นคือ \[\begin{eqnarray}
\mathrm{Pr}(H = 2|C = 1)
&=& \mathrm{Pr}(R = 1, H = 2|C = 1) +
\mathrm{Pr}(R = 2, H = 2|C = 1)
\nonumber \\
&\;& \quad
+
\mathrm{Pr}(R = 3, H = 2|C = 1)
\nonumber \\
&=& 1/6 + 0 + 1/3 = 3/6 = 1/2
\nonumber .
\end{eqnarray}\] ดังนั้น สรุปได้ว่า
| โอกาสเมื่อยืนยันประตูเดิม | \(\mathrm{Pr}(R = 1|C =1, H = 2) = (1/6)/(1/2) = 1/3\) |
| โอกาสเมื่อเปลี่ยนประตูใหม่ | \(\mathrm{Pr}(R = 3|C =1, H = 2) = (1/3)/(1/2) = 2/3\). |
2.2.4 ตัวแปรสุ่มต่อเนื่อง
ตัวแปรสุ่ม \(X\) จะเรียกว่า เป็นตัวแปรสุ่มต่อเนื่อง (continuous random variable) ก็ต่อเมื่อ ฟังก์ชันการแจกแจง ที่อาจเรียก ฟังก์ชันการแจกแจงสะสม (cumulative distribution function คำย่อ cdf) สามารถแสดงได้ในรูป \[\begin{eqnarray} F(x) = \int_{-\infty}^x f(u) du \quad x \in \mathbb{R} \label{eq: prob continuous rv} \end{eqnarray}\] สำหรับบางฟังก์ชันที่สามารถหาปริพันธ์ได้ (integrable function) \(f: \mathbb{R} \rightarrow [0, \infty)\). ฟังก์ชัน \(f\) นี้จะเรียกว่า ฟังก์ชันความหนาแน่นความน่าจะเป็น (probability density function บางครั้งอาจเรียก ฟังก์ชันความหนาแน่น density function คำย่อ pdf) ของ \(X\).
2.2.4.0.1 สิ่งที่มักสับสน.
ตัวแปรสุ่มต่อเนื่อง มีีคุณสมบัติหลายอย่างที่มักถูกเข้าใจผิด. ทั้งตัวแปรสุ่มวิยุตและตัวแปรสุ่มต่อเนื่องใช้บรรยายเหตุการณ์ ซึ่งเหตุการณ์จะสามารถนำไปหาค่าความน่าจะเป็นได้. ความน่าจะเป็น ยังมีคุณสมบัติเหมือนเดิม ไม่ว่า จะเป็น ความน่าจะเป็นของเหตุการณ์ที่บรรยายด้วยตัวแปรสุ่มวิยุต หรือด้วยตัวแปรสุ่มต่อเนื่อง. นั่นคือ ความน่าจะเป็น มีค่าระหว่างศูนย์ถึงหนึ่ง และผลรวมของความน่าจะเป็นทั้งหมดเป็นหนึ่ง.
แต่ตัวแปรสุ่มวิยุตและตัวแปรสุ่มต่อเนื่องมีคุณสมบัติหลาย ๆ อย่างต่างกัน. กำหนดให้ \(D\) เป็นตัวแปรสุ่มวิยุต และ \(C\) เป็นตัวแปรสุ่มต่อเนื่อง สำหรับตัวแปรสุ่มวิยุต ความน่าจะเป็นของแต่ละผลลัพธ์ คือค่าฟังก์ชันมวลความน่าจะเป็นของค่าผลลัพธ์นั้น นั่นคือ \(\mathrm{Pr}(D = d) = \mathrm{pmf}(d)\). แต่สำหรับตัวแปรสุ่มต่อเนื่อง ความน่าจะเป็นของแต่ละผลลัพธ์เป็นศูนย์เสมอ ไม่ว่าค่านั้นจะเป็นเท่าไร นั่นคือ \(\mathrm{Pr}(C = c) = 0\).
แม้ว่า ความน่าจะเป็นของแต่ละค่าเป็นศูนย์ แต่ความน่าจะเป็นของช่วงค่าสามารถหาได้. วิธีประเมินความน่าจะเป็น ในกรณีตัวแปรสุ่มต่อเนื่อง จะใช้ฟังก์ชันการแจกแจง \(F(c) = \mathrm{Pr}(C \leq c)\) และความน่าจะเป็น \(\mathrm{Pr}(C > c) = 1 - F(c)\). เมื่อต้องการประเมินความน่าจะเป็นเป็นช่วง ก็สามารถทำได้โดย \(\mathrm{Pr}(c_0 < C \leq c_1) = F(c_1) - F(c_0)\). หากต้องการประเมินความน่าจะเป็นบริเวณรอบ ๆ ค่าใดก็สามารถทำได้โดย \(\mathrm{Pr}(c - \epsilon < C \leq c + \epsilon) = F(c + \epsilon) - F(c - \epsilon)\) เมื่อ \(\epsilon\) ระบุระยะของบริเวณรอบ ๆ. ข้อควรระวัง ถ้า \(\epsilon\) เล็กมาก ๆ แล้ว \(\mathrm{Pr}(c - \epsilon < C \leq c + \epsilon)\) จะใกล้กับศูนย์ (ความน่าจะเป็นของค่าจุดจุดหนึ่งของตัวแปรสุ่มต่อเนื่องเป็นศูนย์).
ตัวแปรสุ่มวิยุตมี \(\mathrm{pmf}\) แต่ไม่มี \(\mathrm{pdf}\). ตัวแปรสุ่มต่อเนื่องมี \(\mathrm{pdf}\) ไม่มี \(\mathrm{pmf}\). ค่าของ \(\mathrm{pmf}(d) \in [0,1]\) สำหรับทุก ๆ ค่า \(d\) เพราะว่าค่าของ \(\mathrm{pmf}(d)\) คือค่าความน่าจะเป็น. แต่ค่าของ \(\mathrm{pdf}(c) \geq 0\) ซึ่งอาจจะใหญ่กว่า \(1\) ได้. อย่างไรก็ตาม \[\begin{eqnarray} \int_{-\infty}^{\infty} \mathrm{pdf}(c) dc &=& F(\infty) = \mathrm{Pr}(C \leq \infty) = 1 \nonumber \end{eqnarray}\]
ตาราง 1.4 สรุปคุณสมบัติของตัวแปรสุ่มต่อเนื่อง ที่มักถูกเข้าใจผิด เปรียบเทียบกับคุณสมบัติของตัวแปรสุ่มวิยุตในประเด็นเดียวกัน.
| ประเด็น | ตัวแปรสุ่มวิยุต \(D\) | ตัวแปรสุ่มต่อเนื่อง \(C\) |
|---|---|---|
| ฟังก์ชัน | \(\mathrm{pmf}\) | \(\mathrm{pdf}\) |
| ช่วงค่า | \(\mathrm{pmf}: \mathbb{R} \rightarrow [0, 1]\) | \(\mathrm{pdf}: \mathbb{R} \rightarrow [0, \infty)\) |
| ความน่าจะเป็น | \(\mathrm{Pr}(D = d) = \mathrm{pmf}(d)\) | \(\mathrm{Pr}(C = c) = 0\) |
| \(\mathrm{pdf}\) ไม่ใช่ค่าความน่าจะเป็น | ||
| ฟังก์ชันการแจกแจง | \(F(d) = \mathrm{Pr}(D \leq d)\) | \(F(c) = \mathrm{Pr}(C \leq c)\) |
| \(F(d)= \sum_{u \leq d} \mathrm{pmf}(u)\) | \(F(c)= \int_{-\infty}^c \mathrm{pdf}(u) du\) | |
| ค่าคาดหมาย | \(E[D] = \sum_d d \cdot \mathrm{pmf}(d)\) | \(E[C] = \int_{-\infty}^{\infty} c \cdot \mathrm{pdf}(c) dc\) |
[tbl: prob continuous rv]
2.2.4.0.2 การแจกแจงเกาส์เซียน.
คุณสมบัติที่สำคัญของตัวแปรสุ่ม \(X\) ก็คือ การแจกแจง \(F(x) = \mathrm{Pr}(X \leq x)\). การแจกแจงแบบต่อเนื่อง ชนิดหนึ่งที่สำคัญ คือ การแจกแจงเกาส์เซียน (Gaussian distribution) หรืออาจเรียกว่า การแจกแจงปกติ (normal distribution).
การแจกแจงเกาส์เซียน อธิบายการแจกแจงของตัวแปรสุ่มต่อเนื่อง \(X\) ด้วยฟังก์ชันความหนาแน่น \[\begin{eqnarray} f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( - \frac{(x - \mu)^2}{2 \sigma^2} \right), \quad -\infty < x < \infty \label{eq: prob gaussian pdf} \end{eqnarray}\] เมื่อ \(\mu\) และ \(\sigma^2\) เป็นพารามิเตอร์ของแบบจำลอง 7. ฟังก์ชันการแจกแจงของการแจกแจงเกาส์เซียน ไม่มีรูปแบบปิด (closed form ซึ่งในคณิตศาสตร์ หมายถึง นิพจน์ที่สามารถเขียนโดยใช้การคำนวณพื้นฐานได้) และฟังก์ชันการแจกแจง มักเขียนในรูป \[\begin{eqnarray} F(x) = \frac{1}{2} \left( 1 + \mathrm{erf} \left(\frac{x - \mu}{\sigma \sqrt{2}} \right) \right) \label{eq: prob gaussian cdf} \end{eqnarray}\] เมื่อ \[\begin{eqnarray} \mathrm{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x \exp \left( -t^2 \right) dt \label{eq: prob gaussian erf}. \end{eqnarray}\]
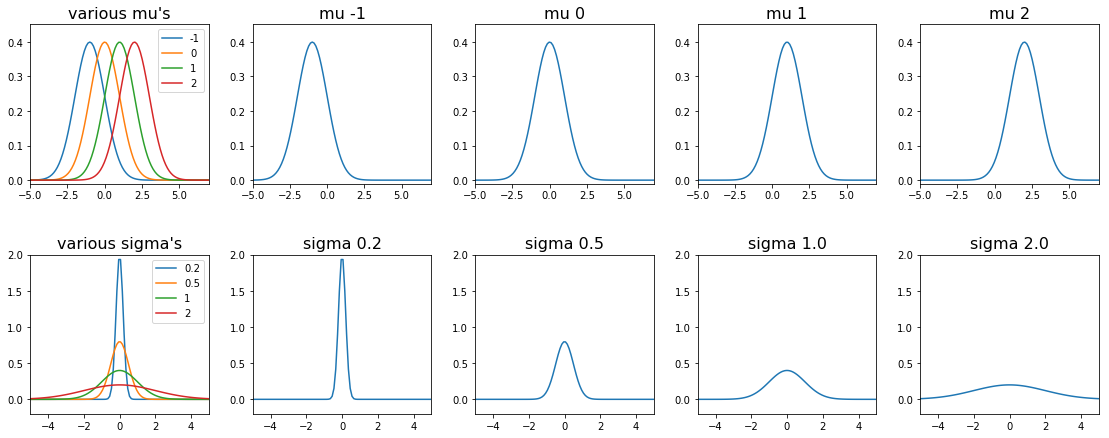
รูป 1.12 แสดงความสัมพันธ์ระหว่างพารามิเตอร์ \(\mu\) กับ \(\sigma\) และผลต่อค่าความหนาแน่นความน่าจะเป็นของการแจกแจงเกาส์เซียน. ค่า \(\mu\) จะควบคุมตำแหน่งที่มีความหนาแน่นสูงสุด. ค่า \(\sigma\) ควบคุมการแผ่. สังเกตว่า ความหนาแน่นความน่าจะเป็น มีค่าเกินหนึ่งได้ (ภาพล่างที่สองจากซ้าย \(\sigma = 0.2\)).
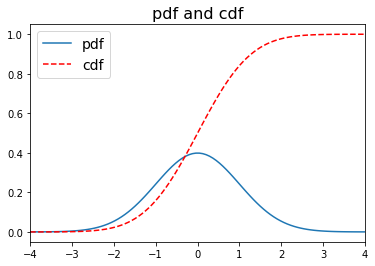
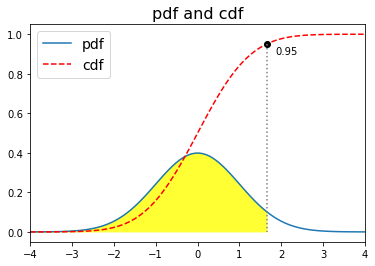
รูป 1.14 แสดงความหนาแน่นความน่าจะเป็น (pdf) และการแจกแจงความน่าจะเป็น (cdf). สังเกตว่า การแจกแจงความน่าจะเป็น จะเป็นฟังก์ชันเพิ่ม (increasing function) เพราะว่า การแจกแจงความน่าจะเป็น \(F(x) = \mathrm{Pr}(X \leq x)\) ดังนั้น ที่ค่ามากขึ้น ความน่าจะเป็นจะไม่มีทางน้อยลง และที่อนันต์ \(F(\infty) = 1\). การแจกแจงความน่าจะเป็น เป็นค่าปริพันธ์ (integral) ของความหนาแน่นความน่าจะเป็น ดังนั้น พื้นที่ใต้กราฟของความหนาแน่นความน่าจะเป็น จนถึง ณ จุดที่สนใจ จะเท่ากับค่าการแจกแจงความน่าจะเป็น.
 |
 |
| ก | ข |
2.3 การหาค่าดีที่สุด
การรู้จำรูปแบบ และการเรียนรู้ของเครื่อง ถูกสร้างบนพื้นฐานของศาสตร์การหาค่าดีที่สุด 8 การรู้จำรูปแบบ ต้องการค้นหารูปแบบที่สนใจออกมา และต้องการให้ผลการค้นหานั้นผิดพลาดน้อยที่สุด. การเรียนรู้ของเครื่อง ต้องการที่จะทำภาระกิจที่ได้รับมอบหมาย ให้ได้สมรรถนะสูงสุด จากประสบการณ์ที่มี.
การหาค่าดีที่สุด (optimization) คือ การหาค่าของปัจจัย (แทนด้วยตัวแปร) ที่มีผลให้เป้าหมาย (แทนด้วยฟังก์ชันของตัวแปร) มีค่าน้อยที่สุด (หรือมีค่ามากที่สุด ขึ้นกับเป้าหมายที่ต้องการ). ปัจจัยที่ต้องการเลือก เรียกว่า ตัวแปรตัดสินใจ (decision variable) และฟังก์ชันแทนเป้าหมาย ซึ่งประมาณความสัมพันธ์ระหว่างค่าของตัวแปรตัดสินใจและเป้าหมายที่ต้องการ เรียกว่า ฟังก์ชันจุดประสงค์ (objective function).
ตัวอย่าง ปัญหาการหาค่าดีที่สุด เช่น การเลือกอุณหภูมิบ่มทุเรียน และเป้าหมายคือได้ทุเรียนสุก ซึ่งวัดจากปริมาณน้ำตาล. ถ้าปัจจัยค่าอุณหภูมิ แทนด้วยตัวแปร \(x\) และถ้ามีฟังก์ชัน \(h\) ที่สามารถใช้ในการประมาณความสัมพันธ์ ระหว่างอุณหภูมิที่บ่มกับปริมาณน้ำตาลที่ได้ ดังนั้นตัวแปร \(x\) คือตัวแปรตัดสินใจ และฟังก์ชัน \(h\) คือฟังก์ชันจุดประสงค์. ถ้าปริมาณน้ำตาลที่ได้มาก เป็นดัชนีบอกว่าทุเรียนสุกดี กรณีนี้คือ การหาค่า \(x\) ที่ทำให้ได้ค่าฟังก์ชัน \(h\) ที่มากที่สุด.
2.3.0.0.1 ปัญหาค่ามากที่สุด และปัญหาค่าน้อยที่สุด.
การหาค่าตัวแปรตัดสินใจ ที่ทำให้ได้ฟังก์ชันจุดประสงค์มีค่ามากที่สุด นั้นเรียกว่า ปัญหาค่ามากที่สุด (maximization problem). ตัวอย่างปัญหาการเลือกอุณหภูมิบ่มทุเรียน ข้างต้นเป็น การหาค่าดีที่สุดแบบปัญหาค่ามากที่สุด. \[\textit{ปัญหาค่ามากที่สุด} ใช้สัญกรณ์ \begin{eqnarray} \underset{x}{\mathrm{maximize}} & h(x) \label{eq: opt max prob} \end{eqnarray}\] หรือ อาจเขียนย่อเป็น \(\mathrm{max}_x \; h(x)\) ซึ่งระบุว่า ต้องการหาค่าของตัวแปรตัดสินใจ \(x\) ที่ทำให้ฟังก์ชันจุดประสงค์ \(h(x)\) มีค่ามากที่สุด.
ทำนองเดียวกัน การหาค่าตัวแปรตัดสินใจ ที่ทำให้ได้ฟังก์ชันจุดประสงค์มีค่าน้อยที่สุด นั้นเรียกว่า ปัญหาค่าน้อยที่สุด (minimization problem). ตัวอย่างปัญหาค่าน้อยที่สุด เช่น การหาเส้นทางขับรถจากขอนแก่นไปร้อยเอ็ด ที่ใช้เวลาเดินทางน้อยที่สุด (ตัวแปรตัดสินใจเลือกเส้นทาง และฟังก์ชันจุดประสงค์ประมาณเวลาเดินทาง) การหาทำเลตั้งเสาสัญญาณวิทยุ ที่ใช้งบประมาณรวมน้อยที่สุด (ตัวแปรตัดสินใจเลือกตำแหน่งที่ตั้งเสาสัญญาณ และฟังก์ชันจุดประสงค์ประเมินงบประมาณรวม) การหารูปแบบการจัดรูปร่างของโปรตีน ที่ใช้พลังงานน้อยที่สุด (ตัวแปรตัดสินใจเลือกรูปร่างของโปรตีน และฟังก์ชันจุดประสงค์คำนวณพลังงานที่ใช้). \[\textit{ปัญหาค่าน้อยที่สุด} ใช้สัญกรณ์ \begin{eqnarray} \underset{x}{\mathrm{minimize}} & h(x) \label{eq: opt min prob} \end{eqnarray}\] หรือ อาจเขียนย่อเป็น \(\mathrm{min}_x \; h(x)\) ซึ่งระบุว่า ต้องการหาค่าของตัวแปรตัดสินใจ \(x\) ที่ทำให้ฟังก์ชันจุดประสงค์ \(h(x)\) มีค่าน้อยที่สุด. บางครั้ง สัญกรณ์อาจระบุเซตของค่าตัวแปรตัดสินใจที่ใช้ค้นหา เช่น \(\mathrm{min}_{x \in \mathbb{R}} \; h(x)\) ซึ่งระบุว่า ค่าของตัวแปรตัดสินใจสามารถเป็นจำนวนจริงใด ๆ หรือ \(\mathrm{min}_{\boldsymbol{x} \in \mathbb{R}^2} \; h(\boldsymbol{x})\) ระบุว่า ค่าของตัวแปรตัดสินใจเป็นเวกเตอร์ที่มีสองส่วนประกอบจำนวนจริง.
ปัญหาค่าน้อยที่สุดและปัญหาค่ามากที่สุด จริง ๆ แล้ว เป็นเสมือนเรื่องเดียวกันที่มองจากคนละมุม. ปัญหาค่าน้อยที่สุดและปัญหาค่ามากที่สุด สามารถแปลงไปมาระหว่างกันได้. นั่นคือ การหาตัวแปรตัดสินใจ \(x\) ที่ทำให้ฟังก์ชันจุดประสงค์ \(h(x)\) มีค่ามากที่สุด จะเทียบเท่ากับการหาค่า \(x\) ที่ทำให้ \(-h(x)\) มีค่าน้อยที่สุด. นั่นคือ \(\mathrm{max}_x \; h(x)\) \(\equiv\) \(\mathrm{min}_x \; -h(x)\). รูป 1.15 แสดงภาพเปรียบเทียบค่าฟังก์ชัน \(h(x)\) และ \(-h(x)\) ที่เปรียบเสมือนภาพภูเขา และเงาของภาพภูเขาที่สะท้อนน้ำ โดยค่าของฟังก์ชันจะพลิกกลับรอบ ๆ ค่าศูนย์ (ค่าบวกเปลี่ยนเป็นลบ ค่าลบเปลี่ยนเป็นบวก ค่าศูนย์อยู่ที่เดิม ค่าบวกมากอยู่สูงจะเปลี่ยนเป็นค่าลบมากอยู่ต่ำ เป็นต้น).
ดังนั้นเพื่อความสะดวก ตำรานี้จะอ้างถึง ปัญหาค่าน้อยที่สุด แทนปัญหาการหาค่าดีที่สุด โดยเฉพาะ เมื่ออภิปรายถึงวิธีการที่ใช้แก้ปัญหา ซึ่งเมื่อปัญหาทั้งสองแบบเทียบเท่ากัน วิธีต่าง ๆ ที่แก้ปัญหาค่าน้อยที่สุดได้ ก็สามารถใช้แก้ปัญหาค่ามากที่สุดได้เช่นกัน.
หมายเหตุ ฟังก์ชันจุดประสงค์ อาจถูกเรียกด้วยชื่ออื่น ๆ เช่น ฟังก์ชันค่าใช้จ่าย (cost function), ฟังก์ชันความสูญเสีย (loss function), ฟังก์ชันพลังงาน (energy function), ฟังก์ชันผลประโยชน์ (utility function) และ ฟังก์ชันคุณค่า (value function). ชื่อเหล่านี้ คือฟังก์ชันจุดประสงค์. แต่ชื่อของฟังก์ชันเหล่านี้ อาจบ่งบอกได้ชัดเจนกว่าว่า ปัญหาเป็นปัญหาค่าน้อยที่สุด (เช่น ฟังก์ชันค่าใช้จ่าย, ฟังก์ชันความสูญเสีย และฟังก์ชันพลังงาน) หรือปัญหาเป็นปัญหาค่ามากที่สุด (เช่น ฟังก์ชันผลประโยชน์ และฟังก์ชันคุณค่า). ชื่อเหล่านี้ มีการใช้อย่างกว้างขวางตามศาสตร์ ตามสาขาวิชา และตามงานประยุกต์ใช้งานด้านต่าง ๆ เช่น เศรษฐศาสตร์ มักใช้ฟังก์ชันผลประโยชน์, ศาสตร์การวิจัยปฏิบัติการ (operation research) มักพบคำว่า ฟังก์ชันค่าใช้จ่าย. ศาสตร์การเรียนรู้ของเครื่อง มักเลือกใช้คำว่า ฟังก์ชันความสูญเสีย. ส่วนคำว่า ฟังก์ชันพลังงาน อาจพบเห็นได้บ้าง ในงานทางด้านการประมวลผลภาพ.
ผลลัพธ์จากการหาค่าดีที่สุด คือ ค่าของตัวแปรตัดสินใจ ที่ทำให้ฟังก์ชันจุดประสงค์มีค่าน้อยที่สุด. ค่าที่ได้นี้ เรียกว่า ค่าทำให้น้อยที่สุด (minimizer) และนิยมใช้สัญลักษณ์เป็นตัวแปรตัดสินใจตามด้วยตัวยกที่เป็นดาว เช่น \(x^\ast\) เพื่อระบุว่า กำลังกล่าวถึง ค่าทำให้น้อยที่สุดที่หามาเสร็จแล้ว ไม่ใช่ \(x\) ที่เป็น ตัวแปรตัดสินใจ ที่อาจใช้ค่าใด ๆ ก็ได้. หมายเหตุ ค่าทำให้น้อยที่สุด โดยทั่วไปจะไม่ใช่ค่าที่น้อยที่สุด. รูป 1.16 แสดงแกนนอนแทนค่าของตัวแปรตัดสินใจ \(x\) และแกนตั้งแทนค่าของฟังก์ชันจุดประสงค์ \(f(x)\). ค่า \(x\) ที่น้อยที่สุด แทนด้วยสัญกรณ์ \(x_{\min}\) คือ \(-\infty\) เพราะว่า \(-\infty\) เป็นค่าที่น้อยที่สุดของจำนวนจริง และไม่ได้มีข้อจำกัดค่าของ \(x\) (ดูหัวข้อ 1.3.2 สำหรับกรณีปัญหาแบบมีข้อจำกัด). ค่าทำให้น้อยที่สุด \(x^\ast = x_1\) เพราะว่า ที่ค่า \(x_1\) ทำให้ฟังก์ชันจุดประสงค์มีค่าน้อยที่สุด นั่นคือ \(f(x_1) = f_{\min}\) หรือ \(f(x_1) \leq f(x)\) สำหรับทุก ๆ ค่าของ \(x\).
สัญกรณ์ \(\mathrm{min}_x \; f(x)\) นี้ใช้เพื่อระบุเป้าหมายและตัวแปรที่เกี่ยวข้องเท่านั้น. หากต้องการระบุความสัมพันธ์ในสมการ อาจใช้สัญกรณ์ เช่น \(v = \arg\min_x f(x)\) เพื่อระบุว่า ค่า \(v = x^\ast\) ที่หาได้จากการแก้ปัญหา \(\min_x f(x)\). หากต้องการระบุค่าฟังก์ชันจุดประสงค์ที่น้อยที่สุด อาจระบุด้วยสัญกรณ์ เช่น \(f(x^\ast)\) หรือ สัญลักษณ์ เช่น \(f_{\min}\) เป็นต้น.
2.3.0.0.2 ค่าทำให้น้อยที่สุดท้องถิ่น และค่าทำให้น้อยที่สุดทั่วหมด.
จากรูป 1.16 สังเกตว่า แม้ \(x_1\) จะเป็นค่าทำให้น้อยที่สุด แต่ \(x_2, x_3, x_4, x_5, x_6\) ก็มีลักษณะที่น่าสนใจ. ค่า \(x_1, x_2, x_3, x_4, x_5, x_6\) ทั้งหมด จะเป็น ค่าทำให้น้อยที่สุดท้องถิ่น. ค่าทำให้น้อยที่สุดท้องถิ่น (local minimizers) คือ ค่าของตัวแปรตัดสินใจ ที่ทำให้ฟังก์ชันจุดประสงค์มีค่าน้อยกว่าหรือเท่ากับค่าฟังก์ชันจุดประสงค์จากบริเวณรอบ ๆ. กล่าวอีกอย่างได้ว่า ค่าทำให้น้อยที่สุดท้องถิ่น คือ ค่าที่ทำให้ฟังก์ชันจุดประสงค์มีค่าน้อยที่สุดในท้องถิ่น (ไม่มีใครในละแวกที่น้อยเกิน). ค่า \(x_1, x_2, x_3, x_4, x_5, x_6\) ต่างก็ทำให้ค่าฟังก์ชันจุดประสงค์น้อยกว่าหรือเท่ากับค่าจากบริเวณรอบ ๆ แต่ค่า \(x_1\) นอกจากจะทำให้ \(f(x_1)\) มีค่าน้อยกว่าค่าจากบริเวณรอบ ๆ แล้ว (ซึ่งทำให้ \(x_1\) เป็นค่าทำให้น้อยที่สุดท้องถิ่น) ค่า \(f(x_1)\) ยังน้อยที่สุดทุกที่ด้วย. ค่าตัวแปรตัดสินใจ ที่ทำให้ฟังก์ชันจุดประสงค์มีค่าน้อยกว่าหรือเท่ากับ ฟังก์ชันจุดประสงค์ของค่าตัวแปรทุกตัวที่เป็นไปได้ เรียกว่า ค่าทำให้น้อยที่สุดทั่วหมด (global minimizer). กล่าวอีกอย่างได้ว่า ค่าทำให้น้อยที่สุดทั่วหมด คือ ค่าที่ทำให้ฟังก์ชันจุดประสงค์มีค่าน้อยที่สุดทั่วหมดทุกที่ (ไม่มีใครในหล้าที่น้อยเกิน). ค่าทำให้น้อยที่สุดทั่วหมด จะเป็นค่าทำให้น้อยที่สุดท้องถิ่นด้วยเสมอ. แต่ค่าทำให้น้อยที่สุดท้องถิ่น อาจไม่ใช่ค่าทำให้น้อยที่สุดทั่วหมด. สถานการณ์ที่ การแก้ปัญหาค่าดีที่สุด แล้วได้ค่าทำให้น้อยที่สุดท้องถิ่น แต่ไม่ใช่ค่าทำให้น้อยที่สุดทั่วหมด มักถูกอ้างถึงว่าเป็น สถานการณ์ที่ดีที่สุดท้องถิ่น (local optimum).
สังเกตว่า บริเวณ \(x_3\) และ \(x_4\) จะเป็นที่เสมือนที่ราบ ซึ่งนอกจาก \(x_3\) และ \(x_4\) ค่าบริเวณนั้นก็จะให้ฟังก์ชันจุดประสงค์ที่เท่ากัน ค่า \(x\) บริเวณที่ราบนั้น ก็จะเรียกว่าเป็น ค่าทำให้น้อยที่สุดท้องถิ่นได้ทั้งหมด เพราะว่า รอบ ๆ ข้างไม่มีใครทำให้ฟังก์ชันจุดประสงค์น้อยเกินได้. ค่า \(x_5\) ก็เป็นค่าทำให้น้อยที่สุดท้องถิ่น แต่เป็นลักษณะที่เรียกว่า จุดอานม้า (saddle point).
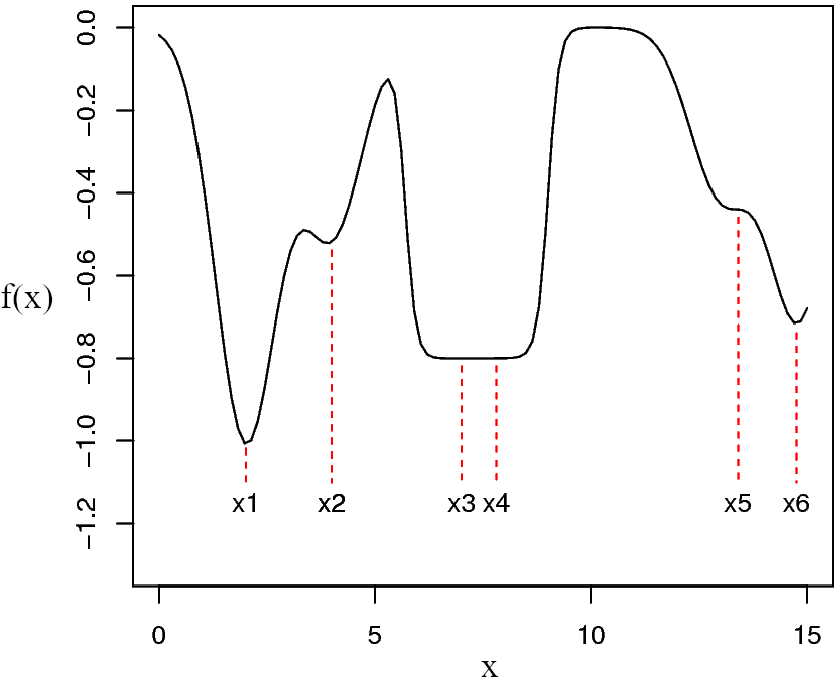
2.3.1 การแก้ปัญหาด้วยวิธีลงเกรเดียนต์
ศาสตร์การหาค่าดีที่สุดนั้นกว้างขวาง และมีการประยุกต์ใช้ที่หลากหลาย. สำหรับการประยุกต์ใช้กับงานการรู้จำรูปแบบ และการเรียนรู้ของเครื่อง ลักษณะปัญหา มักจะถูกตีกรอบออกมาให้ตัวแปรตัดสินใจ \(\boldsymbol{v} \in \mathbb{R}^n\) เมื่อ \(n\) เป็นจำนวนเต็มมีค่าตั้งแต่หนึ่งขึ้นไป และฟังก์ชันจุดประสงค์ \(g\) เป็นฟังก์ชันที่สามารถหาอนุพันธ์ได้ (differentiable function). การมีฟังก์ชันจุดประสงค์ที่สามารถหาอนุพันธ์ได้ ช่วยให้สามารถใช้ขั้นตอนวิธีแก้ปัญหาค่าน้อยที่สุด ที่มีประสิทธิภาพได้.
วิธีลงเกรเดียนต์ (gradient descent algorithm) เป็นขั้นตอนวิธี (algorithm) สำหรับปัญหาค่าน้อยที่สุด. วิธีลงเกรเดียนต์เป็นขั้นตอนวิธีที่เรียบง่าย และใช้ได้ผลดี โดยเฉพาะกับปัญหาขนาดไม่ใหญ่มาก. แนวคิดของวิธีลงเกรเดียนต์ คือ การใช้ค่าเกรเดียนต์ ช่วยในการหาค่าของตัวแปรตัดสินใจ โดย การเริ่มต้นด้วย ค่าของตัวแปรตัดสินใจ ค่าหนึ่ง และคำนวณค่าเกรเดียนต์ ณ จุดนั้นออกมา แล้วใช้ค่าเกรเดียนต์ที่ได้ บอกทิศทางในการปรับค่าของตัวแปรตัดสินใจ ว่าควรปรับเพิ่มหรือลด มากน้อยเท่าไร ดำเนินการปรับค่าตัวแปรตัดสินใจ และวนทำไปเรื่อย ๆ จนพบจุดที่เป็นค่าทำให้น้อยที่สุด.
เกรเดียนต์ ซึ่งเป็นอนุพันธ์ของฟังก์ชันจุดประสงค์ต่อตัวแปรตัดสินใจ จะบอกอัตราการเปลี่ยนค่าของฟังก์ชันจุดประสงค์ เมื่อตัวแปรตัดสินใจเพิ่มค่าขึ้น. ดังนั้นหากเกรเดียนต์เป็นบวกและมีค่ามาก นั่นหมายถึง ถ้าเพิ่มค่าตัวแปรตัดสินใจขึ้น แล้วฟังก์ชันจุดประสงค์จะมีค่าเพิ่มขึ้นมาก. หากค่าของเกรเดียนต์เป็นบวกแต่มีขนาดเล็ก การเพิ่มค่าตัวแปรตัดสินใจขึ้น จะไปเพิ่มค่าฟังก์ชันจุดประสงค์ขึ้น แต่ไม่มาก และหากเกรเดียนต์เป็นลบ เมื่อเพิ่มค่าตัวแปรตัดสินใจขึ้น ค่าฟังก์ชันจุดประสงค์จะลดลง. ดังนั้นเกรเดียนต์จึงสามารถใช้เป็นเสมือนเงื่อนงำ ที่บอกทิศทางที่จะปรับค่าตัวแปรตัดสินใจ เพื่อลดค่าฟังก์ชันจุดประสงค์ลงไปเรื่อย ๆ จนไปถึงค่าฟังก์ชันจุดประสงค์ที่น้อยที่สุดได้. สมการ \(\eqref{eq: opt gd}\) แสดงการคำนวณค่าตัวแปรตัดสินใจ ด้วยวิธีลงเกรเดียนต์ \[\begin{eqnarray} \boldsymbol{v}^{(k+1)} &=& \boldsymbol{v}^{(k)} - \alpha \nabla g(\boldsymbol{v}^{(k)}) \label{eq: opt gd} \end{eqnarray}\] เมื่อ ตัวแปร \(\boldsymbol{v}^{(k+1)}\) เป็นค่าใหม่ของตัวแปรตัดสินใจ (ที่ได้จากการคำนวณครั้งที่ \(k+1\)) และ ตัวแปร \(\boldsymbol{v}^{(k)}\) เป็นค่าเดิมของตัวแปรตัดสินใจ (ที่ได้จากการคำนวณครั้งที่ \(k\)) และ เกรเดียนต์ \(\nabla g(\boldsymbol{v}^{(k)})\) คือค่าเกรเดียนต์ของฟังก์ชันจุดประสงค์ ที่ค่าเดิมของตัวแปรตัดสินใจ (ค่าตัวแปรตัดสินใจที่ได้จากการคำนวณครั้งที่ \(k\)) และค่าสเกล่าร์ \(\alpha > 0\) เรียกว่า ขนาดก้าว (step size) เป็นค่าที่ใช้ควบคุมอัตราเร็วในการปรับค่าของตัวแปรตัดสินใจ.
แนวคิดนี้ อุปมาเหมือน คนที่อยู่บนยอดเขาสูง ที่หมอกลงมากจนมองอะไรไม่เห็น และต้องการกลับบ้านที่อยู่พื้นล่าง. เปรียบฟังก์ชันจุดประสงค์ เป็นเหมือนระดับความสูงของพื้นที่ ณ จุดที่ยืนอยู่ และตัวแปรตัดสินใจเป็นเหมือนตำแหน่งเส้นรุ้งเส้นแวง (latitude-longitude location) ณ จุดที่ยืนอยู่ ตัวแปร \(\boldsymbol{v}^{(k)}\) ก็เสมือนตำแหน่งที่ยืนอยู่ปัจจุบัน และเกรเดียนต์ \(\nabla g(\boldsymbol{v}^{(k)})\) ก็เหมือนความชัน ณ ตำแหน่งที่ยืนปัจจุบัน ที่บอกว่าทิศทางไหนที่รู้สึกว่าพื้นชันขึ้น. ถ้าต้องการกลับบ้าน หรือไปตำแหน่งที่ระดับความสูงที่ต่ำที่สุด วิธีคือ ขยับจากจุดที่ยืนปัจจุบันไปจุดใหม่ โดยขยับไปในทิศทางลง (ซึ่งคือ ทิศทางตรงข้ามกับทิศที่พื้นชันขึ้น ได้แก่ ทิศ \(-\nabla g(\boldsymbol{v}^{(k)})\)) โดยต้องค่อย ๆ เดิน ค่อย ๆ ก้าวเล็ก ๆ เพราะถ้าก้าวยาวเกินไป อาจก้าวข้ามทางเดินลงเขาแคบ ๆ ที่จะกลับบ้านได้ และขนาดก้าว \(\alpha\) ก็เป็นค่าที่ใช้คุมไม่ให้ก้าวยาวเกินไป หลังจากก้าวไปแล้ว ตอนนี้ ตำแหน่งที่ยืนก็จะเปลี่ยนใหม่เป็น \(\boldsymbol{v}^{(k+1)}\) และก็ขยับแบบนี้อีก ทำซ้ำเรื่อย ๆ จนกลับถึงบ้าน.
2.3.1.0.1 ตัวอย่าง.
การหาค่าทำให้น้อยที่สุดของ \(f(x) = - e^{ - (x-5)^2 }\) ด้วยวิธีลงเกรเดียนต์.
เริ่มต้นด้วยการเลือกจุดเริ่มต้น สมมติเลือก \(x^{(0)} = 6.5\) และเลือกใช้ค่าขนาดก้าว สมมติเลือกเป็น \(\alpha = 0.5\). เกรเดียนต์สามารถวิเคราะห์การคำนวณไว้ได้ \[\begin{eqnarray} \nabla f(x) &=& \frac{d f(x)}{d x} = - e^{ - (x-5)^2 } \cdot (-2 x + 10). \nonumber \end{eqnarray}\]
ปรับค่าตัวแปรตัดสินใจ ตามสมการ \(\eqref{eq: opt gd}\)
\[\begin{eqnarray} %(k=1) &\;& \mbox{การคำนวณครั้งแรก } (k=1) \nonumber \\ x^{(1)} &=& x^{(0)} - (0.5) \cdot \nabla f (x^{(0)}) = 6.5 - (0.5) \cdot \nabla f (6.5) \nonumber \\ &=& 6.5 - (0.5) \cdot \left(- e^{ - (6.5-5)^2 } \cdot (-2 \cdot (6.5) + 10) \right) = 6.3419. \nonumber \\ %(k=2) &\;& \mbox{การคำนวณที่สอง } (k=2) \nonumber \\ x^{(2)} &=& x^{(1)} - (0.5) \cdot \nabla f (x^{(1)}) = 6.3419 - (0.5) \cdot \nabla f (6.3419) = 6.1202 \nonumber \\ &\;& \mbox{การคำนวณต่อ ๆ มา} \nonumber \\ x^{(3)} &=& 6.1202 - (0.5) \cdot \nabla f (6.1202) = 5.8009 \nonumber \\ x^{(4)} &=& 5.8009 - (0.5) \cdot \nabla f (5.8009) = 5.3792 \nonumber \end{eqnarray}\] และ \(x^{(5)} = 5.0508\); \(x^{(6)} = 5.0001\); \(x^{(7)} = 5.0000\); \(x^{(8)} = 5.0000\).และผลลู่เข้าสู่ \(x = 5\) ซึ่งคือค่าทำให้น้อยที่สุด. ส่วน \(f(5) = -1\) เป็นค่าฟังก์ชันจุดประสงค์ที่น้อยที่สุด และค่าเกรเดียนต์ ณ จุดนี้คือ \(\nabla f(5) = 0\). \(\square\)
สังเกตว่า ที่ค่าทำให้น้อยที่สุด \(x^\ast\) จะทำให้เกรเดียนต์ \(\nabla f(x^\ast) = 0\) และนี่คือ ธรรมชาติ 9 ของค่าทำให้น้อยที่สุด ซึ่งคือ ณ จุดค่าทำให้น้อยที่สุด เกรเดียนต์จะมีค่าเป็นศูนย์ 10 ดังนั้น ถึงแม้จะคำนวณต่อ ค่าของตัวแปรตัดสินใจก็จะยังคงติดอยู่ที่ค่าทำให้น้อยที่สุด.
2.3.1.0.2 การใช้งานวิธีลงเกรเดียนต์.
วิธีลงเกรเดียนต์ มีอภิมานพารามิเตอร์ เป็นค่าขนาดก้าว. อภิมานพารามิเตอร์ (meta-parameter หรือ hyper-parameter) หมายถึง ปัจจัยระดับสูงของวิธีการคำนวณ แต่ละวิธี ที่ผู้ใช้ต้องเลือกให้เหมาะสม. สำหรับวิธีลงเกรเดียนต์ ผู้ใช้ต้องเลือกค่าของขนาดก้าว. ถ้าเลือกใช้ขนาดก้าวที่มีค่าเล็กพอ วิธีลงเกรเดียนต์ จะรับประกันการลู่เข้าได้ 11. การลู่เข้า (convergence) หมายถึง พฤติกรรมที่ดีของผลการคำนวณ สำหรับการคำนวณลักษณะการวนซ้ำขัดเกลา (iterative refinement computation) นั่นคือ ค่าของผลการคำนวณของแต่ละรอบคำนวณ มีการเปลี่ยนแปลงน้อยลง เมื่อรอบการคำนวณเพิ่มมากขึ้น อาจกล่าวได้ว่า การลู่เข้าคือพฤติกรรมที่ ผลลัพธ์จากการคำนวณเปลี่ยนแปลงค่าเข้าหา(ลู่เข้าหา)ค่าใดค่าหนึ่ง ในลักษณะคงที่ เมื่อรอบการคำนวณเพิ่มมากขึ้น.
ขนาดก้าวที่ใหญ่เกินไป อาจทำให้การคำนวณล้มเหลวได้ แต่ขนาดก้าวที่เล็กเกินไป อาจทำให้ต้องทำการคำนวณหลายรอบมาก ๆ ซึ่งมีผลให้ใช้เวลาในการคำนวณนาน (ดูแบบฝึกหัด [ex: opt gd step size] ประกอบ). ในทางปฏิบัติ เพื่อให้ไม่เสียเวลาคำนวณมากเกินไป เงื่อนไขการจบการคำนวณ (terminating condition) มักถูกใช้ประกอบ. เงื่อนไขการจบที่นิยมใช้กับวิธีลงเกรเดียนต์ ได้แก่ เงื่อนไขจำนวนรอบสูงสุด (maximum number of iterations) และ เงื่อนไขความคลาดเคลื่อนยินยอม (tolerance).
เงื่อนไขจำนวนรอบสูงสุด จะกำหนดจำนวนรอบที่จะหยุดทำการคำนวณ ไม่ว่าการคำนวณนั้น จะดำเนินไปถึงสิ้นสุดหรือไม่ จะได้ค่าทำให้น้อยที่สุดแล้วหรือไม่. นั่นคือ กำหนด \(\boldsymbol{v}^{(k+1)} = \boldsymbol{v}^{(k)} - \alpha \nabla g (\boldsymbol{v}^{(k)})\) สำหรับ \(k = 1, \ldots, N_{\max}\) เมื่อ \(N_{\max}\) คือจำนวนรอบคำนวณที่มากที่สุด และการใช้เงื่อนไขนี้ จะทำให้ผู้ใช้ต้องกำหนดจำนวนรอบสูงสุดนี้ด้วย. ดังนั้นอภิมานพารามิเตอร์ จะมีจำนวนรอบสูงสุดขึ้นอีกตัว.
เงื่อนไขความคลาดเคลื่อนยินยอม กำหนดค่าความคลาดเคลื่อนที่ยอมรับได้ ซึ่งอาจเลือกใช้เงื่อนไข ขนาดของเกรเดียนต์ \(\epsilon = \|\nabla g(\boldsymbol{v}^{(k+1)})\|\). แบบฝึกหัด [ex: opt gd simple code] แสดงตัวอย่างโปรแกรมวิธีลงเกรเดียนต์อย่างง่าย ที่ใช้เงื่อนไขการจบแค่จำนวนรอบสูงสุด. แบบฝึกหัด [ex: opt gd termination code] แสดงตัวอย่างโปรแกรมวิธีลงเกรเดียนต์ที่ใช้เงื่อนไขคลาดเคลื่อนยินยอม.
วิธีลงเกรเดียนต์ประยุกต์ใช้ได้ง่าย ต้องการแค่เกรเดียนต์ และค่าเริ่มต้น. ค่าเริ่มต้นก่อนการคำนวณของตัวแปรตัดสินใจ อาจเป็นค่าใดก็ได้ 12 แต่โดยทั่วไป มักนิยมใช้การกำหนดค่าเริ่มต้น (initialization) ให้กับตัวแปรตัดสินใจ ด้วยค่าที่สุ่มขึ้นมา. (ดูแบบฝึกหัด [ex: opt gd random.norm init])
ปัญหาที่ตัวแปรตัดสินใจมีหลาย ๆ ตัว สามารถใช้วิธีลงเกรเดียนต์ได้ โดยการจัดหลาย ๆ ตัวแปรตัดสินใจ เข้ามารวมกันเป็นเวกเตอร์ตัวแปรตัดสินใจเวกเตอร์เดียว และวิธีลงเกรเดียนต์เตรียมการมาสำหรับกรณีนี้อยู่แล้ว (สมการ \(\eqref{eq: opt gd}\)). สังเกตว่า ตัวแปรตัดสินใจเขียนเป็นเวกเตอร์ และอัตราการเปลี่ยนก็ใช้เกรเดียนต์ แต่การนำวิธีลงเกรเดียนต์ ไปเขียนโปรแกรมเพื่อทำงานกับเวกเตอร์ จะต้องระวังเรื่องของตัวแปรเป็นพิเศษ. (ดูแบบฝึกหัด [ex: opt gd vec code] ประกอบ) นอกจากนั้น เพื่อช่วยให้สามารถตรวจสอบความก้าวหน้า ในการหาค่าทำให้น้อยที่สุดได้อย่างมีประสิทธิภาพ ควรตรวจสอบค่าฟังก์ชันจุดประสงค์ทุก ๆ รอบคำนวณ. ตัวอย่างต่อไปนี้ แสดงการคำนวณของวิธีลงเกรเดียนต์ เมื่อตัวแปรตัดสินใจมีสองค่า.
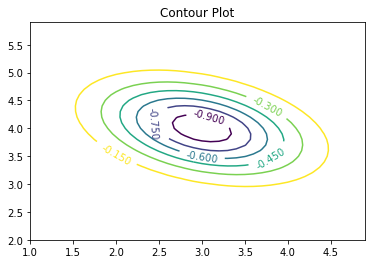 |
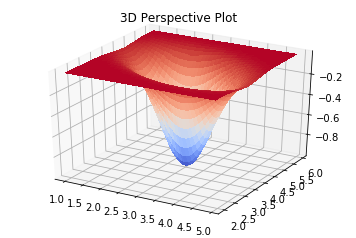 |
| ก | ข |
2.3.1.0.3 ตัวอย่าง เมื่อตัวแปรตัดสินใจเป็นเวกเตอร์.
ปัญหา เช่น \(\min_{\boldsymbol{v}} \; g\) เมื่อ \(\boldsymbol{v} =[v_1, v_2]^T\) และ \(g(\boldsymbol{v}) = -e^{-53-v_1^2 -2v_2^2-v_1 v_2 + 10 v_1 + 19 v_2}\) ซึ่งรูป 1.18 แสดงฟังก์ชันจุดประสงค์ในรูปคอนทัวร์ (contour plot) และในรูปสามทัศนมิติ (3d perspective plot) ปัญหานี้สามารถแก้ด้วยวิธีลงเกรเดียนต์ ดังนี้.
เลือกอภิมานพารามิเตอร์ ได้แก่ ค่าขนาดก้าว \(\alpha = 0.01\)
เตรียมฟังก์ชันคำนวณเกรเดียนต์ \[\begin{eqnarray} \nabla g(\boldsymbol{v}) &=& \begin{bmatrix} \frac{\partial g}{\partial v_1} \\ \frac{\partial g}{\partial v_2} \end{bmatrix} = \begin{bmatrix} g(\boldsymbol{v}) \cdot (-2 v_1 - v_2 + 10) \\ g(\boldsymbol{v}) \cdot (-4 v_2 - v_1 + 19) \end{bmatrix} = g(\boldsymbol{v}) \cdot \begin{bmatrix} -2 v_1 - v_2 + 10 \\ -4 v_2 - v_1 + 19 \end{bmatrix} \nonumber . \end{eqnarray}\] สังเกต ค่าฟังก์ชันจุดประสงค์ \(g(\boldsymbol{v})\) เป็นสเกล่าร์ แต่ค่าเกรเดียนต์ \(\nabla g(\boldsymbol{v})\) เป็นเวกเตอร์ ที่มีสัดส่วน (จำนวนส่วนประกอบ) เท่ากับสัดส่วนของตัวแปรตัดสินใจ \(\boldsymbol{v}\).
สุ่มเลือกค่าเริ่มต้น สมมติว่าสุ่มได้ \(\boldsymbol{v}^{(0)} = [2.5, 3.5]^T\)
ปรับค่าตัวแปรตัดสินใจ ตามสมการ \(\eqref{eq: opt gd}\)
\[\begin{eqnarray} %(k=1) &\;& \mbox{การคำนวณครั้งแรก } (k=1) \nonumber \\ \boldsymbol{v}^{(1)} &=& \boldsymbol{v}^{(0)} - (0.01) \cdot \nabla g (\boldsymbol{v}^{(0)}) \nonumber \\ &=& [2.5, 3.5]^T - 0.01 \cdot (-0.3679) \cdot [-2(2.5)-3.5+10, -4(3.5)-2.5+19]^T \nonumber \\ &=& [2.5, 3.5]^T - 0.01 \cdot [-0.5518, -0.9197]^T = [2.506, 3.509]^T \nonumber \\ &\;& \mbox{การคำนวณที่สอง } (k=2) \nonumber \\ \boldsymbol{v}^{(2)} &=& \boldsymbol{v}^{(1)} - (0.01) \cdot \nabla g (\boldsymbol{v}^{(1)}) \nonumber \\ &=& [2.506, 3.509]^T - 0.01 \cdot [-0.5615, -0.9326]^T = [2.511, 3.519]^T \nonumber \\ &\;& \mbox{การคำนวณที่สาม } (k=3) \nonumber \\ \boldsymbol{v}^{(3)} &=& \boldsymbol{v}^{(2)} - (0.01) \cdot \nabla g (\boldsymbol{v}^{(2)}) \nonumber \\ &=& [2.511, 3.519]^T - 0.01 \cdot [-0.5711, -0.9452]^T = [2.517, 3.528]^T \nonumber \nonumber \end{eqnarray}\]และเมื่อดำเนินการคำนวณต่อไป (ดูแบบฝึกหัด [ex: opt gd vec code] ประกอบ) จะพบว่า \(\boldsymbol{v}^{(300)} = [2.997, 4.001]^T\), \(\boldsymbol{v}^{(400)} = [2.999, 4.000]^T\), \(\boldsymbol{v}^{(500)} = [3.000, 4.000]^T\), \(\boldsymbol{v}^{(600)} = [3.000, 4.000]^T\). ค่าของ \(\boldsymbol{v}\) ปรับน้อยมาก ๆ จนถึงแทบไม่ปรับเลยในรอบคำนวณหลัง ๆ นี่คือ \(\boldsymbol{v}\) ลู่เข้าหา \([3, 4]^T\). รูป 1.19 แสดงการปรับค่าตัวแปรตัดสินใจ ในรูปเส้นทางบนภาพคอนทัวร์ 13 ของฟังก์ชันจุดประสงค์. รูป 1.20 แสดง ความก้าวหน้า (progress) ของการดำเนินการหาค่าทำให้น้อยที่สุด. \(\square\)
จากรูป 1.20 ค่าของตัวแปรตัดสินใจ \(\boldsymbol{v}\) ทั้งสองค่า จะปรับเข้าหา \([3, 4]^T\) นั่นคือคำตอบลู่เข้า. เมื่อดูที่จุดลู่เข้า ดังที่ได้อภิปรายมาแล้ว ขนาดของเกรเดียนต์จะเป็นศูนย์ที่จุดดีที่สุด (optimal point) ซึ่งเป็นจุดที่ตัวแปรตัดสินใจปรับค่าไปอยู่ที่ค่าทำให้น้อยที่สุด. ขนาดของเกรเดียนต์จึงนิยมใช้เป็นเงื่อนไขในการจบโปรแกรม เพื่อไม่ต้องคำนวณมากรอบเกินไป เช่นกรณีนี้ จะเห็นว่าทำการคำนวณแค่ราว ๆ \(500\) รอบก็เห็นการลู่เข้าชัดเจนแล้ว. เมื่อดูที่ฟังก์ชันจุดประสงค์ (ภาพ Loss บนซ้าย) ค่าฟังก์ชันจุดประสงค์จะน้อยลงเรื่อย ๆ ถ้าเลือกค่าขนาดก้าวไม่ใหญ่เกินไป. พฤติกรรมการทำงานของวิธีลงเกรเดียนต์จะมีลักษณะเช่นนี้ คือ ค่าฟังก์ชันจุดประสงค์จะลดลง เมื่อรอบคำนวณเพิ่มขึ้น. การดูค่าฟังก์ชันจุดประสงค์ต่อรอบคำนวณเช่นนี้ สะดวก เพราะสามารถตรวจสอบได้ ไม่ว่าตัวแปรตัดสินใจจะมีจำนวนเท่าใด และถูกใช้เป็นแนวทางปฎิบติ เพื่อติดตามความก้าวหน้า และวิเคราะห์การทำงานของการแก้ปัญหาค่าน้อยที่สุด ว่าดำเนินการได้ดีมากน้อยเพียงใด.
![เส้นทางการหาค่าทำให้น้อยที่สุด จุดวงกลมสีดำแสดงจุดเริ่มต้น (ตำแหน่ง [2.5, 3.5]^T) และจุดดาวสีแดงแสดงจุดสุดท้าย (ตำแหน่ง [3, 4]^T). เส้นทางระหว่างจุดทั้งสอง คือค่าต่าง ๆ ที่ตัวแปรตัดสินใจถูกปรับตั้งแต่รอบคำนวณแรก ๆ ไปจนถึงรอบคำนวณท้าย ๆ.](02Background/opt/code_opt_2Dgd_trajectory.png)
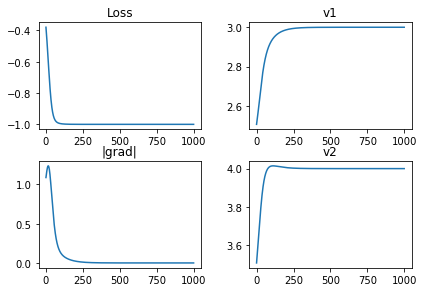
วิธีลงเกรเดียนต์:
“ไม่ว่าเราเริ่มต้นอยู่ที่ไหน ถ้าเราขยับไปทิศทางที่ดีขึ้นเรื่อย ๆ
เราจะไปถึงจุดที่ดีที่สุดได้ เพียงต้องทำเรื่อย ๆ และไม่รีบเกินไป”
2.3.2 การหาค่าดีที่สุดแบบมีข้อจำกัด
การหาค่าดีที่สุดที่ได้อภิปรายมา ค่าของตัวแปรตัดสินใจเป็นค่าจำนวนจริงใด ๆ ซึ่งเขียนเป็นสัญกรณ์ทั่ว ๆ ไป \(\mathrm{min}_{\boldsymbol{v}} g(\boldsymbol{v})\) โดย \(\boldsymbol{v} \in \mathbb{R}^n\) เมื่อ \(n\) เป็นจำนวนเต็มที่มีค่าตั้งแต่หนึ่งเป็นต้นไป การหาค่าดีที่สุดแบบนี้ ไม่ได้มีเงื่อนไขจำกัดค่าของตัวแปรตัดสินใจ (นอกจากเป็นจำนวนจริง) และการหาค่าดีที่สุดแบบนี้ จะเรียกว่า การหาค่าดีที่สุดแบบไม่มีข้อจำกัด (unconstrained optimization).
กรณีที่มีข้อจำกัดของค่าของตัวแปรตัดสินใจ จะเรียกว่า การหาค่าดีที่สุดแบบมีข้อจำกัด (constrained optimization) และจะใช้สัญกรณ์ เพื่อระบุข้อจำกัดอย่างชัดเจน เช่น \[\begin{eqnarray} \underset{\boldsymbol{v}}{\mathrm{minimize}} & g(\boldsymbol{v}) \nonumber \\ \mbox{subject to} & \boldsymbol{v} \in \Omega \label{eq: opt contrained opt} \end{eqnarray}\] เมื่อ \(\boldsymbol{v} \in \mathbb{R}^n\) เป็นตัวแปรตัดสินใจ ฟังก์ชัน \(g: \mathbb{R}^n \rightarrow \mathbb{R}\) เป็นฟังก์ชันจุดประสงค์ และเซต \(\Omega\) เป็นเซตย่อยของ \(\mathbb{R}^n\) ที่ระบุค่าของตัวแปรตัดสินใจในช่วงที่สนใจ หรือกลุ่มค่าที่ยอมรับได้. ค่าคำตอบของ \(\boldsymbol{v}\) ที่ได้จะต้องอยู่ในเซตย่อยนี้. เซต \(\Omega\) นี้ เรียกว่า เซตข้อจำกัด (constraint set หรือ เซตที่เป็นไปได้ feasible set). กรณีที่ \(\Omega = \mathbb{R}^n\) ปัญหาในกรณีนี้จะเป็น การหาค่าดีที่สุดแบบไม่มีข้อจำกัด. สัญกรณ์ \(\eqref{eq: opt contrained opt}\) อาจเขียนย่อเป็น \(\mathrm{min}_{\boldsymbol{v}} \; g(\boldsymbol{v}) \; \mbox{s.t.} \; \boldsymbol{v} \in \Omega\).
จากตัวอย่าง การหาอุณหภูมิบ่มทุเรียน ถ้ากำหนดว่า อุณหภูมิบ่มต้องอยู่ในช่วง \(30\) ถึง \(80\) องศาเซลเซียส (เพราะว่าเตาบ่มที่มี ทำอุณหภูมิได้ในช่วงแค่นั้น) ปัญหานี้จะเป็นการหาค่าดีที่สุดแบบมีข้อจำกัด และอาจเขียนเป็น สัญกรณ์ \(\mathrm{max}_t \; \mathrm{sugar}(t) \; \mbox{s.t.} \; 30 \leq t \leq 80\) เมื่อ \(t\) แทนอุณหภูมิบ่มในหน่วยองศาเซลเซียส ฟังก์ชัน \(\mathrm{sugar}\) ประเมินระดับน้ำตาลที่ได้ จากการบ่มด้วยอุณหภูมิ \(t\) และข้อจำกัด \(30 \leq t \leq 80\) ระบุค่าของ \(t\) ที่ใช้ได้ว่า อยู่ในช่วง \(30\) ถึง \(80\). (ปัญหาค่ามากที่สุดนี้ เทียบเท่า ปัญหาค่าน้อยที่สุด \(\mathrm{min}_t \; -\mathrm{sugar}(t) \; \mbox{s.t.} \; 30 \leq t \leq 80\) )
2.3.2.0.1 ค่าทำให้น้อยที่สุดท้องถิ่น และค่าทำให้มากที่สุดทั่วหมด.
ในกรณีที่มีข้อจำกัด ค่าของตัวแปรตัดสินใจจะพิจารณาจากค่าที่เป็นไปได้ (feasible) เท่านั้น. ค่าทำให้น้อยที่สุดท้องถิ่น คือ ค่าของตัวแปรตัดสินใจ ที่ทำให้ฟังก์ชันจุดประสงค์มีค่าน้อยกว่าหรือเท่ากับค่าฟังก์ชันจุดประสงค์ของค่าที่เป็นไปได้บริเวณรอบ ๆ. นั่นคือ ถ้ากำหนดให้ \(g: \mathbb{R}^n \rightarrow \mathbb{R}\) เป็นฟังก์ชันค่าจริง ที่นิยามสำหรับเซต \(\Omega \subset \mathbb{R}^n\) แล้ว จุด \(\boldsymbol{v}^\ast \in \Omega\) เป็นค่าทำให้น้อยที่สุดท้องถิ่น ของฟังก์ชัน \(g\) บนเซต \(\Omega\) ถ้ามีค่า \(\epsilon > 0\) ที่ \(g(\boldsymbol{v}) \geq g(\boldsymbol{v}^\ast)\) สำหรับทุกค่าของ \(\boldsymbol{v} \in \Omega \setminus \{ \boldsymbol{v}^\ast \}\) และ \(\|\boldsymbol{v} - \boldsymbol{v}^\ast\| < \epsilon\). ส่วนค่าทำให้น้อยที่สุดทั่วหมด คือ ค่าของตัวแปรตัดสินใจ ที่ทำให้ฟังก์ชันจุดประสงค์มีค่าน้อยกว่าหรือเท่ากับค่าฟังก์ชันจุดประสงค์ของค่าที่เป็นไปได้อื่น ๆ ทุกค่า. นั่นคือ จุด \(\boldsymbol{v}^\ast \in \Omega\) จะเป็นค่าทำให้น้อยที่สุดทั่วหมดของฟังก์ชัน \(g\) บนเซต \(\Omega\) ถ้า \(g(\boldsymbol{v}) \geq g(\boldsymbol{v}^\ast)\) สำหรับ ทุกค่าของ \(\boldsymbol{v} \in \Omega \setminus \{ \boldsymbol{v}^\ast \}\).
2.3.2.0.2 วิธีแก้ปัญหาค่าน้อยที่สุดแบบมีข้อจำกัด.
มีสองแนวทางหลักที่ทั่วไปนิยมใช้แก้ปัญหาค่าน้อยที่สุดแบบมีข้อจำกัด คือ แนวทางการแปลงมุมมอง และแนวทางการลงโทษ.
แนวทางการแปลงมุมมอง (projection approach) จะใช้ฟังก์ชัน \(F: \mathbb{R}^n \rightarrow \Omega\) เพื่อแปลงค่าของตัวแปรตัดสินใจมาเป็นค่าที่เป็นไปได้. ตัวอย่าง เช่น เมื่อใชักับวิธีลงเกรเดียนต์ อาจทำโดย \[\begin{eqnarray} \boldsymbol{v}^{(k+1)} = F \left( \boldsymbol{v}^{(k)} - \alpha \cdot \nabla g(\boldsymbol{v}^{(k)}) \right) \label{eq: opt const projection} \end{eqnarray}\] ในทางปฏิบัติแล้ว ฟังก์ชันแปลง \(F\) นี้ อาจจะยากที่หา หรือยากที่จะคำนวณ ในหลาย ๆ สถานการณ์. งานการเรียนรู้ของเครื่อง มักนิยมใช้แนวทางการลงโทษมากกว่า.
แนวทางการลงโทษ (penalty approach) จะใช้การลงโทษ เมื่อค่าตัวแปรตัดสินใจไม่อยู่ในเซตข้อจำกัด โดยการปรับกรอบปัญหาจากเดิม \(\min_{\boldsymbol{v}} g(\boldsymbol{v}) \; \mbox{s.t.} \; \boldsymbol{v} \in \Omega\) ไปเป็นกรอบปัญหาใหม่ \[\begin{eqnarray} \underset{\boldsymbol{v}}{\mathrm{min}} \; g(\boldsymbol{v}) + \lambda P(\boldsymbol{v}) \label{eq: opt const penalty} \end{eqnarray}\] เมื่อ \(\lambda \in \mathbb{R}\) เป็นพารามิเตอร์ลงโทษ (penalty parameter) ซึ่งนิยมเรียกว่า ลากรานจ์พารามิเตอร์ (Lagrange parameter) และฟังก์ชัน \(P: \mathbb{R}^n \rightarrow [0, \infty)\) เป็นฟังก์ชันต่อเนื่อง (continuous function) เรียกว่า ฟังก์ชันลงโทษ (penalty function) โดย ฟังก์ชันลงโทษจะมีค่าเป็นศูนย์ เมื่อค่าตัวแปรตัดสินในอยู่ในเซตข้อจำกัด นั่นคือ \(P(\boldsymbol{v}') = 0\) สำหรับ \(\boldsymbol{v}' \in \Omega\).
ตัวอย่างเช่น ปัญหา \(\min_x \sin (x) /(1 + x^2) \; \mbox{s.t.} \; x \geq 0\). รูป 1.21 แสดงฟังก์ชันจุดประสงค์ และแสดงส่วนที่ไม่ผ่านเงื่อนไขด้วยแรเงาสีเทา. รูปแสดงให้เห็นว่า จุดที่ทำให้ค่าฟังก์ชันจุดประสงค์น้อยที่สุด มีค่าเป็นลบ แต่จุดนี้ละเมิดข้อจำกัด และใช้เป็นคำตอบไม่ได้. การหาคำตอบด้วยวิธีลงโทษ อาจเลือกใช้ฟังก์ชัน \[\begin{eqnarray} P(x) = \left \{ \begin{array}{l l} 0 & \quad \mbox{เมื่อ} \quad x \geq 0, \\ -x & \quad \mbox{เมื่อ} \quad x < 0. \end{array} \right. \label{eq: opt const penalty function} \end{eqnarray}\] ซึ่งเป็นฟังก์ชันต่อเนื่อง (ทำให้สามารถหาอนุพันธ์ได้ และสามารถใช้วิธีแก้ปัญหา เช่น วิธีลงเกรเดียนต์ได้) และฟังก์ชัน \(P\) ลงโทษค่าที่ละเมิดข้อจำกัดตามปริมาณที่ละเมิด. รูป 1.22 แสดงค่าของฟังก์ชันลงโทษในสมการ \(\eqref{eq: opt const penalty function}\) และเมื่อนำฟังก์ชันลงโทษนี้ ไปใช้ร่วมกับฟังก์ชันจุดประสงค์ ฟังก์ชันที่ปรับใหม่จะเปลี่ยนพฤติกรรมไป ดังแสดงในรูป 1.23.
วิธีใช้การลงโทษนี้ ก็คือ การเปลี่ยนจากปัญหาแบบมีข้อจำกัด กลับมาเป็นปัญหาแบบไม่มีข้อจำกัด โดย การดัดแปลงฟังก์ชันจุดประสงค์ใหม่ เพื่อให้คำตอบ อยู่ในช่วงค่าที่เป็นไปได้. ดังนั้น ขั้นตอนการหาคำตอบต่อไป ก็สามารถดำเนินการได้ โดยใช้วิธีแก้ปัญหา แบบเดียวกับปัญหาแบบไม่มีข้อจำกัด.
รูป 1.23 แสดงให้เห็นว่า เมื่อ ค่าของลากรานจ์พารามิเตอร์ใหญ่มากพอ ค่าทำน้อยที่สุดของฟังก์ชันจุดประสงค์ใหม่ จะถูกบังคับให้อยู่ในช่วงค่าที่เป็นไปได้. กลไกการทำงานของการลงโทษ คือ การลงโทษจะทำให้ คำตอบของปัญหาค่าน้อยที่สุดใหม่ ที่รวมการลงโทษเข้าไป จะเป็น 14 คำตอบของปัญหาค่าน้อยที่สุดแบบมีข้อจำกัดเดิม เมื่อลากรานจ์พารามิเตอร์มีค่าใหญ่มากพอ.
ในทางปฏิบัติ การแก้ปัญหาด้วยวิธีลงโทษ จะเลือกค่าของลากรานจ์พารามิเตอร์มาค่าหนึ่ง และดำเนินการแก้ปัญหา แล้วตรวจสอบค่าคำตอบที่ได้ ว่าอยู่ภายใต้ข้อจำกัดหรือไม่ ถ้าคำตอบที่ได้ อยู่ภายใต้ข้อจำกัด นี่ก็คือ คำตอบของปัญหาที่ใช้ได้. แต่ถ้าคำตอบที่ได้ ไม่อยู่ภายใต้ข้อจำกัด จะต้องเพิ่มค่าของลากรานจ์พารามิเตอร์ขึ้น และดำเนินการแก้ปัญหาอีก และทำเช่นนี้ เพิ่มค่าลากรานจ์พารามิเตอร์ขึ้น จนกว่าจะได้คำตอบที่อยู่ภายใต้ข้อจำกัด.
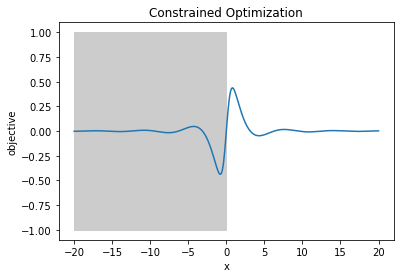
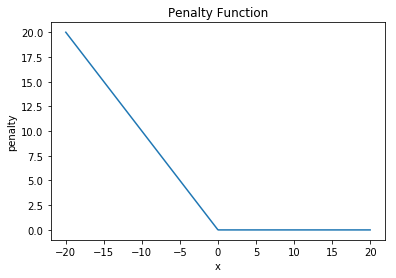
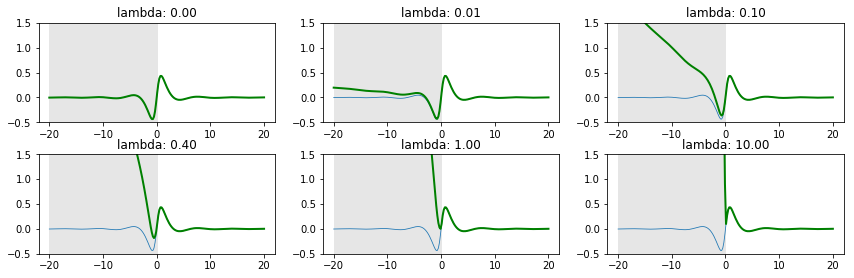
2.3.2.0.3 เกร็ดความรู้ สติปัญญาของลิง
รายการโนวา ออกอากาศสารคดีสติปัญญาของลิงไม่มีหาง เรื่อง “Ape Genius” ทางสถานีโทรทัศน์พีบีเอส ของสหรัฐอเมริกา ในปี ค.ศ. 2008. รายการนำเสนองานศึกษาสติปัญญาของลิงชิมแปนซีและลิงโบโนโบหลาย ๆ งาน (ลิงชิมแปนซีและลิงโบโนโบ มีพันธุ์กรรมต่างจากมนุษย์แค่ประมาณ \(1.2\%\). มนุษย์แต่ละคนมีพันธุ์กรรมแตกต่างกันประมาณ \(0.1\%\)) รายการ พยายามจะตอบคำถาม ที่ถามว่า ลักษณะของสติปัญญาแง่มุมใดที่ต่างกัน และทำให้ชิมแปนซีและโบโนโบไม่สามารถพัฒนาขึ้นมาสร้างอารยธรรม เช่นเดียวกับที่มนุษย์ทำได้.
ความสามารถในการสร้างและใช้เครื่องมือ. มีหลักฐานชัดเจนว่า ลิงชิมแปนซีมีการสร้างและใช้เครื่องมือ เช่น เจน กูดดอล พบลิงชิมแปนซีในแทนซาเนีย ใช้กิ่งไม้ในการล่อมดมากิน และ จิล พริตซ์ พบลิงชิมแปนซีในป่าโฟกอลี ในประเทศเซเนกัล ที่สร้างหอกจากกิ่งไม้ และใช้เป็นเครื่องมือในการล่าหาอาหาร
ความสามารถในการทำงานร่วมกัน. มีหลักฐานหลายอย่างของพฤติกรรมการออกล่าร่วมกันของลิงชิมแปนซี และ สถาบันวิจัยลิงใหญ่ไม่มีหาง (Great Ape Research Institute) ของญี่ปุ่น พบว่า ลิงชิมแปนซีมีความสามารถในการทำงานร่วมกัน มีความสามารถในการขอความช่วยเหลือ และก็สามารถให้ความช่วยเหลือมนุษย์ได้เวลาที่ถูกร้องขอ
ความสามารถในการแก้ปัญหา. การศึกษาหนึ่งทดลอง โดยใส่เมล็ดถั่วไว้ในหลอดยาว ที่ลิงไม่สามารถจะล้วงเข้าไปหยิบได้ และตัวหลอด ก็ยึดติดกับกรงแน่น จนลิงไม่สามารถขยับได้. ลิงใช้เวลาพักหนึ่ง ก่อนจะพบวิธีแก้ปัญหา. มันไปที่บ่อน้ำในกรง อมน้ำแล้วมาพ่นใส่หลอด แล้วอาหารก็ลอยขึ้นบนน้ำ มันเติมน้ำเข้าไป จนอาหารลอยอยู่ในระดับที่เอื้อมถึงได้ สิ่งนี้ แสดงถึงความสามารถในการแก้ปัญหาของลิง.
ความสามารถในการเลียนแบบ. ทีมของนักจิตวิทยาแอนดรู วิทเทนต้องการทดสอบความสามารถในการเลียนแบบของลิง. ทีมสร้างเครื่องกลไกที่ลิงจะต้องทำสองขั้นตอน ได้แก่ หมุนจานให้พอดีช่อง และโยกคันโยก เพื่อจะได้กินอาหาร และนำเครื่องไปทดสอบกับตัวลิง. ลิงไม่สามารถจะหาวิธีทำนี้ได้เอง. แต่ทีมงานค่อย ๆ สอนลิงขึ้นมาตัวหนึ่ง จากนั้นลองให้ลิงตัวอื่นดูลิงตัวนี้ทำงาน แล้วสังเกตว่าลิงตัวอื่น ๆ ก็สามารถเลียนแบบ เพื่อทำงานสองขั้นตอนนี้ได้อย่างง่ายดาย.
ความสามารถทางตัวเลข. เททซูโร มัตซูซาวาแห่งมหาวิทยาลัยเกียวโต นำเสนอผลการทดสอบลิงชิมแปนซีชื่อไอ ที่แสดงความสามารถทางตัวเลข ในการเข้าใจความหมายของตัวเลขอารบิก และยังสามารถรู้ลำดับของตัวเลขได้
ความสามารถทางภาษาและการสื่อสาร. ลิงโบโนโบชื่อคานซี เรียนรู้ภาษาอังกฤษได้เอง โดยไม่ได้ถูกสอนโดยตรง และซู ซาเวจ-รัมบาวแสดงให้เห็นว่าคานซีเข้าใจภาษาอังกฤษและสามารถทำตามคำสั่งได้อย่างถูกต้อง
2.3.2.0.4 ความสามารถที่ลิงไม่มี
ความสามารถที่กล่าวมาข้างต้น เป็นความสามารถที่พบหลักฐานในลิงชิมแปนซีหรือโบโนโบ. แต่ความสามารถที่ลิงชิมแปนซีหรือโบโนโบไม่มี และเป็นปัจจัยสำคัญที่ทำให้ลิงไม่สามารถพัฒนาอารยธรรมขึ้นมาได้ เชื่อว่าคือความสามารถด้านอารมณ์. ลิงชิมแปนซีมีปัญหาที่เห็นได้ชัดเจน คือปัญหาด้านอารมณ์ ทั้งการแก่งแย่งชิงดีกัน ความรุนแรง และที่สำคัญคือ การควบคุมอารมณ์ตัวเอง.
ความสามารถในการควบคุมตัวเอง. การทดลองของแซลลี่ บอยเซนมหาวิทยาลัยรัฐโอไอโอ แสดงให้เห็นโดยให้ลิงเลือกจานอาหารระหว่างจาน สองจาน ที่มีขนมอยู่ไม่เท่ากัน แต่จานที่ลิงเอื้อมมือไปหา จะเป็นจานที่จะไปให้กับลิงอีกตัว. ถ้าเป็นขนมที่อยู่บนจาน ลิงไม่สามารถจะอดใจและเอื้อมไปที่จานที่น้อยกว่าได้ มันจะเอื้อมไปที่จานที่มันเห็นอาหารมากกว่าตลอด. แต่พอแซลลี่ บอยเซนเปลี่ยนจากการที่เอาขนมวางไว้ในจานให้เห็น กลับใช้ตัวเลขซึ่งลิงเข้าใจความหมาย วางไว้แทน. ลิงสามารถเรียนรู้ที่จะเอื้อมไปที่จานที่ตัวเลขน้อยกว่าได้. การทดลองนี้แสดงให้เห็นว่า ลิงชิมแปนซีมีปัญหาในการควบคุมอารมณ์ของตัวมันเอง. เวลาที่มันเห็นอาหารอยู่ มันไม่สามารถควบคุมตัวเพื่อเลือกทางเลือกที่ดีกว่าได้ แต่พอตัดแรงกระตุ้นทางอารมณ์ออก (ใช้ตัวเลขวางแทนอาหารจริง) มันสามารถเลือกทางเลือกที่ดีกว่าได้.
นอกจากการขาดความสามารถในการควบคุมตนเองแล้ว ปัจจัยสำคัญอีกสองอย่างที่รายการสรุปว่า เป็นอุปสรรคที่ทำให้สติปัญญาของลิงไม่อาจสะสม สร้างเสริมไปสู่การพัฒนาในระดับเดียวกับมนุษย์ได้ ก็คือ ความสามารถในการเรียนรู้โดยรับการถ่ายทอดจากคนอื่น (หรือลิงตัวอื่น) และความสามารถในการสอน. แม้เด็กอาจไม่ได้แสดงความสามารถในการแก้ปัญหาได้ดีเท่ากับลิงชิมแปนซี แต่เด็ก ๆ แสดงความสามารถที่สามารถเรียนรู้จากสิ่งที่ถูกสอนได้ดีกว่า สุนัขเองก็ยังมีความสามารถในการเรียนจากการสอนของมนุษย์ได้ดีกว่าลิง.
นอกจากความสามารถในการเรียนจากการถ่ายทอด ความเต็มใจที่จะถ่ายทอด หรือความเต็มใจที่จะสอน ก็เป็นส่วนประกอบสำคัญที่ทำให้การถ่ายทอดความรู้เกิดขึ้นได้ และลิงชิมแปนซีไม่มีทั้งสององค์ประกอบนี้. อารยธรรมของมนุษย์สร้างโดยการส่งผ่านความรู้และปัญญาจากรุ่นสู่รุ่น. แม้ลิงสามารถเรียนรู้จากลิงตัวอื่นได้โดยการเลียนแบบ แต่การเรียนรู้โดยการเลียนแบบนั้นมักจะช้าและตื้นเขิน. บางครั้งยังอาจมีการสูญหายไป จากการเปลี่ยนรุ่นของลิงอีกด้วย. ลิงรุ่นเก่าตายไป ลิงรุ่นใหม่อาจไม่ได้เรียนรู้สิ่งที่ลิงรุ่นเก่ารู้แล้ว หลาย ๆ อย่างที่ลิงรุ่นเก่ารู้แล้ว เช่นวิธีการใช้เครื่องมือ อาจหายไปจากลิงรุ่นใหม่ และอาจใช้เวลาอีกนานกว่าที่ลิงรุ่นใหม่จะพบวิธีใช้เครื่องมืออีกครั้ง.
การควบคุมตัวเอง การเรียนรู้จากการถ่ายทอด และความเต็มใจที่จะสอน เป็นคุณสมบัติที่แยกมนุษย์ออกจากลิง และเป็นพื้นฐานอารยธรรมของมนุษย์.
“... just as a bird needs two wings,
we need both wisdom and compassion.”—Robina Courtin
“... แบบเดียวกับที่นกต้องมีสองปีก
เราต้องมีทั้งปัญญาและเมตตา”—โรบิน่า เคอร์ทิน
2.4 อภิธานศัพท์
- มิติ (dimension):
มุมมอง หรือหมายถึง มิติปริภูมิค่า ที่เป็นจำนวนตัวเลขที่ใช้ เพื่อระบุตำแหน่งของค่าที่สนใจในปริภูมิค่า เช่น เวกเตอร์ \(\boldsymbol{v} \in \mathbb{R}^{12}\) จะอยู่ใน \(12\) มิติปริภูมิค่า หรือหมายถึงลำดับชั้น เช่น เทนเซอร์ \(\boldsymbol{V} \in \mathbb{R}^{2 \times 3 \times 16}\) จะมี \(3\) ลำดับชั้น.
- เทนเซอร์ (tensor):
โครงสร้างลำดับชั้นของตัวเลข.
- นอร์ม (norm):
ขนาดของเวกเตอร์.
- ภาพฉายเชิงตั้งฉาก (orthogonal projection):
การแปลงค่าที่สนใจ ลงไปบนทิศทางใหม่ โดยการคูณกับเวกเตอร์หนึ่งของทิศทางใหม่.
- การแยกส่วนประกอบเชิงตั้งฉาก (orthogonal decomposition):
การแยกส่วนประกอบของค่าที่สนใจออกเป็นส่วน ที่แต่ละส่วนอยู่ในปริภูมิย่อยที่ตั้งฉากกัน โดยปริภูมิย่อยทั้งหมดที่ได้จากการแยกส่วนประกอบ จะแผ่ทั่วปริภูมิเดิม.
- เวกเตอร์ลักษณะเฉพาะ (Eigenvector):
เวกเตอร์ \(\boldsymbol{v} \neq \boldsymbol{0}\) ใด ๆ ที่ทำให้สมการ \(\boldsymbol{A} \boldsymbol{v} = \lambda \boldsymbol{v}\) เป็นจริง เมื่อ \(\boldsymbol{A}\) เป็นเมทริกซ์ที่สนใจ.
- ค่าลักษณะเฉพาะ (Eigenvalue):
ค่าสเกล่าร์ \(\lambda\) ที่คู่กับเวกเตอร์ลักษณะเฉพาะ ในการทำให้สมการ \(\boldsymbol{A} \boldsymbol{v} = \lambda \boldsymbol{v}\) เป็นจริง.
- ความน่าจะเป็น (probability):
ค่าประเมินโอกาสที่จะเกิดเหตุการณ์ที่สนใจ.
- ผลลัพธ์ (outcome):
ผลเฉลย หรือความจริงที่เกิดขึ้น สิ่งที่เกิดขึ้น หรือสิ่งที่ประจักษ์ภายหลัง.
- ปริภูมิตัวอย่าง sample space):
เซตของผลลัพธ์แบบต่าง ๆ ที่เป็นไปได้ทั้งหมด.
- เหตุการณ์ (event):
กลุ่มของผลลัพธ์ที่เป็นไปได้.
- ตัวแปรสุ่ม (random variable):
ตัวแปรที่ใช้อธิบายเหตุการณ์ที่สนใจ ในรูปตัวเลข.
- ฟังก์ชันการแจกแจง (distribution function):
ฟังก์ชันการแจกแจงของตัวแปรสุ่ม \(X\) คือฟังก์ชัน \(F: \mathbb{R} \rightarrow [0,1]\) โดย \(F(x) = \mathrm{Pr}(X \leq x)\).
- ตัวแปรสุ่มวิยุต (discrete random variable):
ตัวแปรสุ่มที่ค่าของมันอยู่ในเซตจำกัด หรืออยู่ในเซตไม่จำกัดแต่นับได้ เช่น \(X \in \{0, \ldots, 255\}\) เซตของเลขศูนย์ถึงสองร้อยห้าสิบห้า หรือ \(Y \in \mathbb{I}\) เซตของเลขจำนวนเต็ม.
- ตัวแปรสุ่มต่อเนื่อง (continuous random variable):
ตัวแปรสุ่ม ที่ฟังก์ชันการแจกแจงของมัน สามารถเขียนได้ในรูป \(F(x) = \int_{-\infty}^x f(u) du\) เมื่อ \(f: \mathbb{R} \rightarrow [0, \infty)\) เป็นฟังก์ชันความหนาแน่น.
- ฟังก์ชันมวลความน่าจะเป็น (probability mass function):
ฟังก์ชันของตัวแปรสุ่มวิยุต ที่ค่าของมันเท่ากับความน่าจะเป็น.
- ฟังก์ชันความหนาแน่นความน่าจะเป็น (probability density function):
ฟังก์ชันของตัวแปรสุ่มต่อเนื่อง ที่ค่าของมันมากกว่าหรือเท่ากับศูนย์. ค่าของฟังก์ชันความหนาแน่น ไม่ใช่ความน่าจะเป็น แต่ค่าปริพันธ์ในช่วงขอบเขตของมัน จะเป็นความน่าจะเป็นของช่วงขอบเขตนั้น.
- ค่าคาดหมาย (expectation):
ค่าเฉลี่ยของตัวแปรสุ่ม.
- ความน่าจะเป็นแบบมีเงื่อนไข (conditional probability):
ค่าประมาณโอกาสที่จะเกิดเหตุการณ์ที่สนใจ เมื่อรู้ผลลัพธ์ของเงื่อนไข.
- ความน่าจะเป็นก่อน (prior probability):
ความน่าจะเป็นของตัวแปรสุ่มที่ต้องการอนุมาน ก่อนที่จะมีข้อมูลประกอบ.
- ความน่าจะเป็นภายหลัง (posterior distribution):
ความน่าจะเป็นของตัวแปรสุ่มที่ต้องการอนุมาน หลังจากรู้ข้อมูลประกอบแล้ว.
- ฟังก์ชันควรจะเป็น (likelihood function):
ฟังก์ชันของค่าของเงื่อนไข ของความน่าจะเป็นแบบมีเงื่อนไข.
- การสลายปัจจัย (marginalization):
การใช้กฎผลรวม เพื่อลดจำนวนตัวแปรสุ่มลง จากความน่าจะเป็นที่พิจารณา.
- การหาค่าดีที่สุด (optimization):
การหาค่าของตัวแปรตัดสินใจ เพื่อให้ได้ค่าเป้าหมายดีที่สุด.
- ตัวแปรตัดสินใจ (decision variable):
ตัวแปรที่ต้องการหาค่าในการหาค่าดีที่สุด.
- ฟังก์ชันจุดประสงค์ (objective function):
ฟังก์ชันที่ใช้ประมาณค่าเป้าหมายในการหาค่าดีที่สุด หรือบางครั้งอาจเรียกว่า ฟังก์ชันสูญเสีย.
- ปัญหาค่าน้อยที่สุด (minimization problem):
การหาค่าดีที่สุด ที่ต้องการให้ค่าฟังก์ชันจุดประสงค์น้อยที่สุด.
- ค่าทำให้น้อยที่สุด (minimizer):
ค่าของตัวแปรตัดสินใจ ที่ทำให้ค่าฟังก์ชันจุดประสงค์น้อยที่สุด.
- ค่าทำให้น้อยที่สุดท้องถิ่น (local minimizer):
ค่าที่ดีกว่า(หรือไม่แย่กว่า)ค่ารอบ ๆ ข้าง ในปัญหาค่าน้อยที่สุด ต่างจากค่าทำให้น้อยที่สุดทั่วหมดที่ดีกว่า(หรือไม่แย่กว่า)ค่าอื่น ๆ ทั้งหมด. ค่าทำให้น้อยที่สุดทั่วหมดจะเป็นค่าทำให้น้อยที่สุดท้องถิ่นด้วยเสมอ แต่ค่าทำให้น้อยที่สุดท้องถิ่นอาจไม่ใช่ค่าทำให้น้อยที่สุดทั่วหมด.
- วิธีลงเกรเดียนต์ (gradient descent algorithm):
ขั้นตอนวิธีหนึ่งในการแก้ปัญหาค่าน้อยที่สุด โดยการคำนวณแบบวนซ้ำ และอาศัยค่าเกรเดียนต์ของฟังก์ชันจุดประสงค์เทียบกับตัวแปรตัดสินใจ.
- ขนาดก้าว (step size):
ค่าสเกล่าร์ที่ใช้ควบคุมความเร็วในการปรับค่าตัวแปรตัดสินใจ ของขั้นตอนวิธีเพื่อแก้ปัญหาค่าน้อยที่สุด เช่น วิธีลงเกรเดียนต์.
- เงื่อนไขการจบ (terminating condition):
เงื่อนไขที่ใช้หยุดการคำนวณ.
- การกำหนดค่าเริ่มต้น (initialization):
การกำหนดค่าเริ่มต้นให้กับตัวแปร.
- การลู่เข้า (convergence):
ผลลัพธ์จากวิธีการคำนวณแบบวนซ้ำที่ค่าของผลลัพธ์เข้าใกล้ค่า ๆ หนึ่งมากขึ้นเรื่อย ๆ เมื่อจำนวนรอบคำนวณเพิ่มขึ้น.