2 แบบฝึกหัด
2.1 แบบฝึกหัดเชิงทฤษฏี
“As to methods there may be a million and then some, but principles are few. The man who grasps principles can successfully select his own methods. The man who tries methods, ignoring principles, is sure to have trouble.”
—Ralph Waldo Emerson
“วิธีการมีเป็นล้านและมากกว่า แต่หลักการมีไม่มาก บุคคลผู้ยึดในหลักการสามารถเลือกวิธีการได้อย่างดี บุคคลผู้ลองแต่วิธีการ ละเลยหลักการ ย่อมแน่นอนว่าจะมีปัญหา”
—ราล์ฟ วัลโด อีเมอร์สัน
2.1.0.0.1 แบบฝึกหัด
จากระบบสมการ \[\begin{eqnarray} x + y + z &=& 6 \label{eq: lin alg exercise singular 1} \\ 2 x + 2 y + 3 z &=& 14 \label{eq: lin alg exercise singular 2} \\ x + y + 4z &=& 15 \label{eq: lin alg exercise singular 3} \end{eqnarray}\] จงวิเคราะห์และอภิปรายว่า ระบบสมการนี้ สามารถหาคำตอบได้หรือไม่ หรือถ้าได้ คำตอบมีชุดเดียว หรือคำตอบมีหลายชุด. สังเกต แต่ละแถว เป็นอิสระเชิงเส้นกัน แต่สดมภ์หนึ่งและสอง (สัมประสิทธิ์ของ \(x\) และ \(y\)) ไม่เป็นอิสระเชิงเส้นกัน จากมุมมองของสารสนเทศที่ได้รับ ถ้าการไม่เป็นอิสระเชิงเส้นกันของแถว หมายถึง สมการที่ได้ไม่ได้ให้สารสนเทศเพียงพอ สมการหนึ่งได้มาจากการแปลงเชิงเส้นของสมการอื่น แล้ว การไม่เป็นอิสระเชิงเส้นกันของสดมภ์ จะหมายถึงอะไร อภิปราย
2.1.0.0.2 แบบฝึกหัด
ความแปรปรวน (variance) เป็นค่าประเมินการแจกแจงของข้อมูลจากค่าเฉลี่ย. ความแปรปรวน อาจถูกสับสนกับเอนโทรปี. เอนโทรปีสารสนเทศ (information entropy) หรือเรียกสั้น ๆ ว่า เอนโทรปี (entropy) เป็นการประมาณค่าคาดหมายของปริมาณสารสนเทศที่ได้รับ. กำหนดให้ตัวแปรสุ่ม \(X\) แทนข้อความที่ได้รับ. ถ้าข้อความที่ได้รับ มีความน่าจะเป็นสูง หมายถึง ข้อมูลมีสารสนเทศน้อย. ถ้า \(\mathrm{Pr}(X = x) = 1\) แปลว่า \(x\) ไม่มีสารสนเทศอะไรอยู่เลย เป็นเรื่องที่รู้กันอยู่แล้ว. ถ้าข้อความที่ได้รับ มีความน่าจะเป็นต่ำ หมายถึง ข้อความมีสารสนเทศมาก เป็นเรื่องใหม่ เป็นเรื่องที่น่าแปลกใจ เป็นข่าวที่คิดไม่ถึง. ปริมาณสารสนเทศของแต่ละข้อความ ถูกนิยามเป็น \(h(x) = -\log_2 \mathrm{Pr}(X = x)\) เมื่อ \(x\) เป็นข้อความที่ได้รับ. ลอการิทึม (logarithm) เป็นฟังก์ชันทางเดียว (monotonic function) และการทำลบ ช่วยให้ได้ความสัมพันธ์ที่ \(h(x)\) ค่าน้อย เมื่อ \(\mathrm{Pr}(X = x)\) ค่ามาก และ \(h(x)\) ค่ามาก เมื่อ \(\mathrm{Pr}(X = x)\) ค่าน้อย นอกจากนั้น ยังช่วยให้ \(h(x)\) มีค่ามากกว่าหรือเท่ากับศูนย์ด้วย. ค่าเฉลี่ย หรือค่าคาดหมายของปริมาณสารสนเทศ \[\begin{eqnarray} H[X] = - \sum_x \mathrm{Pr}(X = x) \cdot \log_2 \mathrm{Pr}(X = x) \label{eq: Entropy} \end{eqnarray}\] จะเรียกว่า เอนโทรปีสารสนเทศ.
จงคำนวณค่าความแปรปรวนและค่าเอนโทรปี ของข้อมูลต่อไปนี้. ข้อมูลชุดที่ 1 มีความน่าจะเป็นดังนี้ \[\begin{eqnarray} \mathrm{Pr}(X = x) = \left\{ \begin{array}{l l} \frac{1}{4} & \quad \mbox{เมื่อ } x = 0 \mbox{ หรือ } x = 1 \mbox{ หรือ } x = 2 \mbox{ หรือ } x = 3, \\ 0 & \quad \mbox{เมื่อ } x \mbox{ เป็นค่าอื่น ๆ}. \end{array} \right. \label{eq: ex prob var entropy dist 1} \end{eqnarray}\]
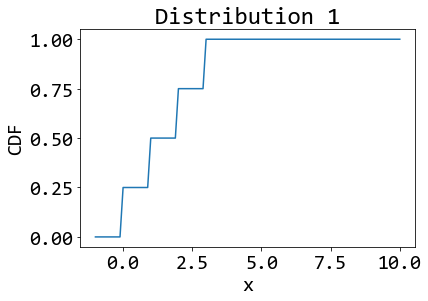
และข้อมูลชุดที่ 2 มีความน่าจะเป็นดังนี้ \[\begin{eqnarray} \mathrm{Pr}(X = x) = \left\{ \begin{array}{l l} \frac{1}{4} & \quad \mbox{เมื่อ } x = 0 \mbox{ หรือ } x = 2 \mbox{ หรือ } x = 4 \mbox{ หรือ } x = 8, \\ 0 & \quad \mbox{เมื่อ } x \mbox{ เป็นค่าอื่น ๆ}. \end{array} \right. \label{eq: ex prob var entropy dist 2} \end{eqnarray}\] รูป 2 แสดงการแจกแจงของข้อมูลทั้งสองชุด. การแจกแจง \(F(x) = \mathrm{Pr}(X \leq x) = \sum_{v \leq x} \mathrm{Pr}(X = v)\). สังเกตผลลัพธ์ของค่าความแปรปรวนและค่าเอนโทรปีที่คำนวณได้. สรุปและอภิปรายค่าความแปรปรวน และค่าเอนโทรปีของข้อมูลสองชุดนี้ พร้อมอภิปรายความต่างกันของค่าความแปรปรวน และค่าเอนโทรปี โดยทั่วไป และยกตัวอย่างลักษณะของข้อมูลที่ทำให้เห็นความต่างชัดเจนประกอบ.
 |
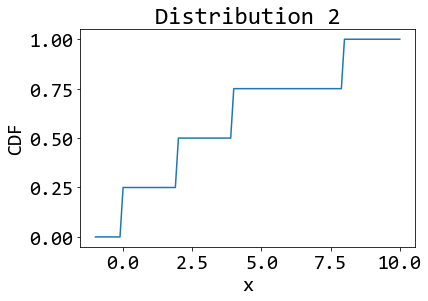 |
คำใบ้ ถ้ากำหนด \(X_1\) เป็นตัวแปรสุ่มของข้อมูลชุดที่ 1 แล้วค่าคาดหมาย \(E[X_1] = \sum_x x \cdot \mathrm{Pr}(X_1 = x) = 0 (1/4) + 1 (1/4) + 2 (1/4) + 3 (1/4) = 1.5\).
2.1.0.0.3 แบบฝึกหัด
จงแก้ปัญหา \(\underset{v}{\mathrm{min}} \; g(v) \mbox{ s.t. } v \leq 2\) เมื่อ \[\begin{eqnarray} % g(v) = 0.2 \log(1 + \exp(-v-3)) % + \frac{1.5}{1 + % \exp(-v +2)} % -2.5 \exp(-0.01 (v - 10)^2) % % g(v) = 0.2 \log(1 + e^{-v-3}) + \frac{1.5}{1 + e^{-v +2}} -2.5 e^{-0.01 (v - 10)^2} % \nonumber \\ \label{eq: ex opt const simple f} \end{eqnarray}\] โดยใช้วิธีการลงโทษ (penalty method) พร้อมอภิปรายว่า (1) กำหนดฟังก์ชันลงโทษเป็นอะไร (2) ฟังก์ชันจุดประสงค์ที่รวมการลงโทษเข้าไปแล้วเป็นอะไร (3) เกรเดียนต์ของฟังก์ชันจุดประสงค์ เกรเดียนต์ของฟังก์ชันลงโทษ และเกรเดียนต์ของฟังก์ชันที่ถูกลงโทษ (ฟังก์ชันจุดประสงค์ ที่รวมการลงโทษเข้าไปแล้ว) เป็นอะไรบ้าง และ (4) คำตอบของปัญหาคืออะไร และเลือกค่าลากรานจ์พารามิเตอร์อย่างไร ยกตัวอย่างค่าที่ทำงานได้ ดูแบบฝึกหัด 1.2.2.0.18 สำหรับผลจากการแก้ปัญหา ด้วยโปรแกรม.
คำใบ้ พจน์แรกในฟังก์ชันจุดประสงค์ ได้แก่ \(0.2 \log(1 + e^{-v-3})\) คือ ฟังก์ชันบวกอ่อน (softplus function) ซึ่งมีรูปพื้นฐานคือ \(\log(1 + e^x)\) และมีอนุพันธ์คือ \(1/(1 + e^{-x})\) ที่เรียกว่า ฟังก์ชันซิกมอยด์ (sigmoid function). พจน์ที่สองได้แก่ \(1.5/(1 + e^{-v +2})\) คือ ฟังก์ชันซิกมอยด์ ที่พึ่งกล่าวไป และฟังก์ชันซิกมอยด์ในรูปพื้นฐาน \(\sigma(x) = 1/(1 + e^{-x})\) มีอนุพันธ์คือ \(e^x / ( 1 + e^x)^2\) หรือเท่ากับ \(\sigma(x) \cdot (1 - \sigma(x))\). พจน์ที่สามได้แก่ \(-2.5 e^{-0.01 (v - 10)^2}\) คือ ฟังก์ชันเกาส์เซียน (Gaussian function) ซึ่งรูปพื้นฐาน \(e^{-x^2}\) มีอนุพันธ์เป็น \(-2 x e^{-x^2}\).
2.1.0.0.4 แบบฝึกหัด
จงแก้ปัญหา \(\underset{v}{\mathrm{min}} \; g(v) \mbox{ s.t. } v \leq -0.5\) เมื่อ \[\begin{eqnarray} g(v) = \left\{ \begin{array}{lcl} -(x + 1) & \mbox{ เมื่อ } & x < -1, \\ x + 1 & \mbox{ เมื่อ } & -1 \leq x < 0, \\ (-x + 1) & \mbox{ เมื่อ } & 0 \leq x < 1, \\ x - 1 & \mbox{ เมื่อ } & x \geq 1. \end{array} \right. \label{eq: ex opt const piecewise f} \end{eqnarray}\]
โดยใช้วิธีการลงโทษ พร้อมอภิปรายว่า (1) กำหนดฟังก์ชันลงโทษเป็นอะไร (2) ฟังก์ชันจุดประสงค์ที่รวมการลงโทษเป็นอะไร (3) เกรเดียนต์ของฟังก์ชันจุดประสงค์ เกรเดียนต์ของฟังก์ชันลงโทษ และเกรเดียนต์ของฟังก์ชันที่ถูกลงโทษ (ฟังก์ชันจุดประสงค์ที่รวมการลงโทษเข้าไปแล้ว) เป็นอะไรบ้าง และ (4) คำตอบของปัญหาคืออะไร และเลือกค่าลากรานจ์พารามิเตอร์อย่างไร ยกตัวอย่างค่าที่ทำงานได้
คำใบ้ อนุพันธ์ของฟังก์ชันต่อเนื่องเป็นช่วง สามารถหาได้ในแต่ละช่วง.
หมายเหตุ ฟังก์ชัน \(g\) เป็นฟังก์ชันต่อเนื่องเป็นช่วง (piecewise continuous function) ซึ่งเป็นกรณีพิเศษ ที่ ณ จุดดีที่สุด ค่าเกรเดียนต์อาจจะไม่เป็นศูนย์.
2.2 แบบฝึกหัดการเขียนโปรแกรม
2.2.1 แบบฝึกหัดไพธอนแก่น
แบบฝึกหัดต่อไปนี้ ทบทวนการเขียนโปรแกรมด้วยภาษาไพธอนพื้นฐาน โดยยังไม่แนะนำให้เรียกใช้มอดูลอื่น ณ ตอนนี้.
2.2.1.0.1 แบบฝึกหัด
จงเขียนฟังก์ชัน add_matrix ที่รับเมทริกซ์สองตัว เป็นอาร์กิวเมนต์ ซึ่งแต่ละตัวเป็นลิสต์ที่มีโครงสร้างสองลำดับมิติ (เหมือนเมทริกซ์) ตรวจสอบ ว่าขนาดของเมทริกซ์เท่ากัน ทำการบวกเมทริกซ์ และรีเทิร์นผลลัพธ์ออกมาในรูปลิสต์ ที่มีโครงสร้างแบบเดียวกัน
2.2.1.0.2 แบบฝึกหัด
จงเขียนฟังก์ชัน mult_matrix ที่รับเมทริกซ์สองตัว เป็นอาร์กิวเมนต์ ซึ่งแต่ละตัวเป็นลิสต์ที่มีโครงสร้างสองลำดับมิติ (เหมือนเมทริกซ์) ตรวจสอบ ว่าขนาดของเมทริกซ์สามารถทำการคูณเมทริกซ์ได้ ทำการคูณเมทริกซ์ และรีเทิร์นผลลัพธ์ออกมาในรูปลิสต์ ที่มีโครงสร้างลักษณะเดียวกัน
2.2.1.0.3 แบบฝึกหัด
การหาเมทริกซ์ผกผัน ด้วยวิธีเกาส์จอร์แดน (Gauss Jordan method) ทำได้โดยขั้นตอนต่อไปนี้. เมื่อต้องการหา \(\boldsymbol{A}^{-1}\) ของเมทริกซ์ \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\)
ขยายเมทริกซ์ \(\boldsymbol{A}\) ด้วยเมทริกซ์เอกลักษณ์. เมทริกซ์ขยาย \(\boldsymbol{A}' \in \mathbb{R}^{n \times 2n}\) จะเป็น \[\begin{eqnarray} \boldsymbol{A}' = \begin{bmatrix} a_{11} & a_{12} & \ldots & a_{1n} & 1 & 0 & \ldots & 0 \\ a_{21} & a_{22} & \ldots & a_{2n} & 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} & 0 & 0 & \ldots & 1 \end{bmatrix} \label{eq: augmented matrix} \end{eqnarray}\]
ดำเนินปฏิบัติการเชิงเส้นกับแถวของ \(\boldsymbol{A}'\) จนส่วนหน้ากลายเป็นเมทริกซ์เอกลักษณ์ ดังเช่น \[\begin{eqnarray} \boldsymbol{B}' = \begin{bmatrix} 1 & 0 & \ldots & 0 & b_{11} & b_{12} & \ldots & b_{1n} \\ 0 & 1 & \ldots & 0 & b_{21} & b_{22} & \ldots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 1 & b_{n1} & b_{n2} & \ldots & b_{nn} \end{bmatrix} \label{eq: linear transformed augmented matrix} \end{eqnarray}\] รายละเอียดการดำเนินปฎิบัติการ คือ (1) ที่แถว \(i\) เพื่อทำให้ส่วนประกอบแนวทะแยงมุมเป็นหนึ่ง ดำเนินการ \(r_{ij} = a_{ij}/a_{ii}\) สำหรับ \(j = 1, \ldots, 2n\) เมื่อ \(r_{ij}\) คือค่าส่วนประกอบภายหลังการคำนวณที่ตำแหน่ง \((i,j)\). (2) ที่แถวอื่น ๆ แถว \(k \neq i\) เพื่อทำให้ส่วนประกอบ ตำแหน่ง \((k,i)\) นอกแนวทะแยงมุมเป็นศูนย์ ดำเนินการ \(s_{kj} = a_{kj} - r_{ij} \cdot a_{ki}\) สำหรับ \(j = 1, \ldots, 2n\) เมื่อ \(s_{ij}\) คือค่าส่วนประกอบภายหลังการคำนวณที่ตำแหน่ง \((i,j)\). (3) ดำเนินการเช่นนี้ โดยทำทุกแถว จากแถว \(i = 1, \ldots, n\) แล้วผลลัพธ์จะได้ \(\boldsymbol{B}'\).
ส่วนหลังของ \(\boldsymbol{B}'\) (สดมภ์ที่ \((n+1)^{th}\) จนถึงสดมภ์สุดท้าย) คือเมทริกซ์ผกผันของ \(\boldsymbol{A}\).
จากโปรแกรมตัวอย่างในรายการ [code: gauss-jordan inverse matrix] จงเขียนโปรแกรมไพธอน เพื่อหาเมตริกผกผันด้วยวิธีเกาส์จอร์แดน และทดสอบผลลัพธ์ที่ได้ โดยใช้การคูณเมทริกซ์ จากแบบฝึกหัด 1.2.1.0.2 แล้วศึกษาโปรแกรม และอภิปรายข้อจำกัด และกรณีที่อาจเสี่ยงทำให้โปรแกรมรันผิดพลาด พร้อมเสนอการปรับปรุงแก้ไข. คำใบ้ การหารด้วยศูนย์จะทำให้โปรแกรมล่มได้.
def gauss_jordan(mat_in):
'''
Do Gauss-Jordan Matrix Inversion.
A: n x n matrix in a list of lists.
Return: Aaug, Ainv
Aaug is the final augmented matrix.
if the front part of Aaug appears to be identity,
Ainv is a valid matrix inversion of A.
'''
# Get dimension
n = len(mat_in)
# Copy a matrix
A = []
for i in range(n):
A.append(mat_in[i].copy())
# Make an identity matrix I
Imat = [[1 * (i == j) for j in range(n)] for i in range(n)]
# Augment A with I
for i in range(n):
A[i].extend(Imat[i])
# Get the front part of A' to identity
for i in range(n):
# Make a diagonal element 1
anchor = A[i][i]
for j in range(i, 2 * n):
A[i][j] /= anchor
# Make an off-diagonal 0
for k in range(n):
if k != i:
target = A[k][i]
for j in range(2 * n):
if target != 0:
A[k][j] = A[k][j] - A[i][j] * target
Ainv = []
for i in range(n):
Ainv.append(A[i][n:])
return A, Ainv
if __name__ == '__main__':
M0 = [[4, 2, 8], [3, 0, 9], [7, 5, 6]]
print('A'); print(M0)
M1, M2 = gauss_jordan(M0)
print('Inverse of A'); print(M2)2.2.2 แบบฝึกหัดไพธอนด้วยนัมไพ
เนื่องจากโปรแกรมการรู้จำรูปแบบ ใช้การคำนวณเชิงเลข (numerical computation) อย่างมาก ดังนั้น การใช้มอดูลการคำนวณเชิงเลขประกอบจึงมีประโยชน์มาก เพื่อช่วยลดภาระ และเพื่อจะได้ทุ่มเทไปที่ศาสตร์ของการรู้จำรูปแบบ และการเรียนรู้ของเครื่องได้เต็มที่มากขึ้น. หัวข้อนี้ แนะนำมอดูลคำนวณเชิงเลข นัมไพ (Numpy) และแมทพล๊อตลิป (Matplotlib) เพื่อช่วยการคำนวณเชิงเลข และการนำไปสร้างภาพให้เห็น (visualization)
นอกจากมอดูลนัมไพ และแมทพล๊อตลิป มีมอดูลที่มีประโยชน์ และนิยมใช้ สำหรับงานรู้จำรูปแบบอีกมาก ซึ่ง ตำรานี้ จะได้แนะนำมอดูลอื่น ๆ อีก ตามเนื้อหาที่เหมาะสมต่อไป
ตัวอย่างโปรแกรมในแบบฝึกหัดต่าง ๆ จากนี้ จะนำเข้ามอดูล numpy และ matplotlib ดัวยคำสั่ง
import numpy as np
from matplotlib import pyplot as pltซึ่งจะนำเข้ามอดูล numpy และ matplotlib.pyplot. มอดูล pyplot เป็นมอดูลย่อย เพื่อใช้ในการวาดกราฟ. การนำเข้านั้น ได้ตั้งชื่อใหม่ให้กับมอดูลทั้งสองเพื่อความสะดวก เป็น np และ plt.
2.2.2.0.1 แบบฝึกหัด
จงสร้างตัวแปร a1 เป็น np.array จาก list เช่น [2, 4, 8, 9] และเรียนรู้คำสั่งต่อไปนี้ คำสั่ง len(a1) คำสั่ง a1.shape คำสั่ง type(a1) คำสั่ง a1.tolist() แล้วสร้าง a2 เป็น np.array จาก list สองมิติ เช่น [[2, 4], [8, 9]] และเรียนรู้คำสั่งแบบเดียวกัน รวมทั้งทดลอง และอภิปรายผลของคำสั่งตัดส่วน (สังเกตชนิด และสัดส่วน ลอง type และ shape) เช่น คำสั่ง a2[0] คำสั่ง a2[0,:] คำสั่ง a2[0][1] และคำสั่ง a2[0,1].
2.2.2.0.2 แบบฝึกหัด
จากคำสั่งต่อไปนี้ ทดลอง ดัดแปลง สังเกต และอภิปรายสิ่งที่ได้เรียนรู้.
คำสั่ง
v1 = np.array([[1,2,3,4]])คำสั่ง
v2 = np.array([[2,4,1,-1]])คำสั่ง
v1 + 5เปรียบเทียบกับคำสั่งv1 + v2และคำสั่งv1 + v2.transpose()คำสั่ง
v1 * 5เปรียบเทียบกับคำสั่งv1 * v2และคำสั่งv1 * v2.transpose()ทดลองแและเปรียบเทียบ การคูณด้วยคำสั่งต่าง ๆ ได้แก่ คำสั่ง
v1*v2คำสั่งnp.dot(v1,v2)คำสั่งnp.multiply(v1,v2)คำสั่งnp.matmul(v1,v2)รวมถึงทดลองเปลี่ยนสัดส่วนของv1และv2เป็นอย่างอื่น (รวมถึงเป็นเมทริกซ์ และเทนเซอร์)
2.2.2.0.3 แบบฝึกหัด
จงทดลองคำสั่งการหาเมทริกซ์ผกผัน np.linalg.inv และหาเมทริกซ์ผกผันต่่อไปนี้ และเปรียบเทียบผลกับแบบฝึกหัด 1.2.1.0.3. \[\begin{eqnarray}
\boldsymbol{A}_1 &=& \begin{bmatrix}
1 & 2 & 4 \\
4 & 0 & 8 \\
7 & 3 & 5
\end{bmatrix}
\nonumber \\
\boldsymbol{A}_2 &=& \begin{bmatrix}
-1 & 2 & 4 \\
4 & 1 & -1 \\
9 & 3 & 8
\end{bmatrix}
\nonumber \\
\boldsymbol{A}_3 &=& \begin{bmatrix}
4 & 0 & 4 \\
1 & 2 & 3 \\
7 & 3 & 10
\end{bmatrix}
\nonumber
\end{eqnarray}\]
2.2.2.0.4 แบบฝึกหัด
จงหาค่าและเวกเตอร์ลักษณะเฉพาะของเมทริกซ์ในแบบฝึกหัด 1.2.2.0.3.
คำใบ้ ฟังก์ชัน numpy.linalg.eig เรียกใช้ เลแพค (LAPACK) ซึ่งเป็นมอดูลที่ได้รับความเชื่่อถือในการคำนวณค่าและเวกเตอร์ลักษณะเฉพาะ. เลแพค ใช้วิธีคำนวณด้วยการแยกตัวประกอบค่าเอกฐาน (singular value decomposition) ที่มีประสิทธิภาพมากกว่า ตัวอย่างวิธีคำนวณที่อภิปรายในหัวข้อ [sec: Eigenvectors and Eigenvalues].
2.2.2.0.5 แบบฝึกหัด
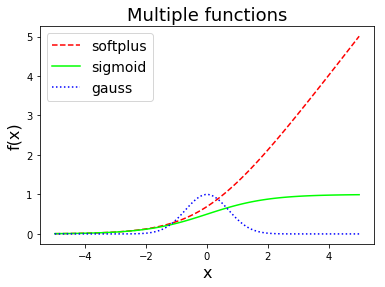
จงเขียนโปรแกรม เพื่อวาดกราฟของฟังก์ชันบวกอ่อน \(f(x) = \log(1 + e^x)\) ฟังก์ชันซิกมอยด์ \(f(x) = 1/(1 + e^{-x})\) และฟังก์ชันเกาส์เซียน \(f(x) = e^{-x^2}\) โดย วาดกราฟทั้งสามให้อยู่ในภาพเดียวกัน ดังแสดงในรูป 3.
คำใบ้ ดูคำสั่ง np.linspace คำสั่ง plt.plot โดยเฉพาะอาร์กิวเมนต์ เช่น color=(1,0.5,0) และ linestyle='--' คำสั่ง plt.legend คำสั่ง plt.title โดยเฉพาะอาร์กิวเมนต์ เช่น fontsize=18.
2.2.2.0.6 แบบฝึกหัด
จงเขียนโปรแกรม โดยใช้มอดูล matplotlib.pyplot เพื่อนำเข้าภาพ (ซึ่งอาจจะเป็นไฟล์นามสกุล .png) แล้วนำมาแสดง ดังตัวอย่างในรูป 5 (ภาพ ก). การดำเนินการนี้ ต้องอ่านภาพเข้ามาก่อน แล้วจึงค่อยแสดงภาพออกหน้าจอ. คำสั่ง เช่น img = plt.imread('t.png') อ่านภาพจากไฟล์ชื่อ 't.png'. ตรวจสอบสัดส่วนข้อมูล และลักษณะข้อมูล เช่น ใช้คำสั่ง print(img.shape) ใช้คำสั่ง print(img). สังเกต plt.imread อ่านภาพ ออกมาเป็นข้อมูลที่มีสัดส่วน \(4\) ลำดับชั้น สำหรับ ช่องสีแดง ช่องสีเขียว ช่องสีน้ำเงิน และช่องอัลฟ่า (alpha channel) และแต่ละพิกเซลมีค่าระหว่าง \(0\) ถึง \(1\). การแสดงภาพทำได้ ด้วยคำสั่ง เช่น plt.imshow(img).
หลังจากนั้นทดลองเปลี่ยนค่าพิกเซลของภาพ แล้วสังเกตผล. ตัวอย่างในรูป 5 ภาพ ข ที่แสดงการเปลี่ยนค่าพิกเซล ด้วยคำสั่ง เช่น img[1000:1010, 1400:1620, 1] = 1 จะเปลี่ยนค่าพิกเซลต่าง ๆ ที่ตำแหน่ง 1000 ถึง 1009 ตามแนวตั้ง และตำแหน่ง 1400 ถึง 1619 ตามแนวนอน ในช่องสีที่หนึ่ง (ช่องสีเขียว) โดยเปลี่ยนค่าเป็นหนึ่ง (ค่ามากที่สุด). เมื่อเปลี่ยนค่าเสร็จแล้ว และนำข้อมูลมาแสดงดูใหม่ จะเห็นเส้นสีเขียวปรากฎขึ้นมา (ภาพ ข มีการเปลี่ยนค่าลักษณะนี้สี่ครั้ง สำหรับสี่เส้นที่เห็นแสดงเป็นกรอบ). หมายเหตุ ถ้ากำหนดค่าใหม่ให้กับพิกเซลแล้ว ภาพนั้นจะมีตำหนิ นั่นคือ เส้นสีเขียวจะไม่สามารถถูกลบออกได้ (แต่ถูกเขียนทับได้). หากต้องการเก็บภาพต้นฉบับไว้ ให้ทำสำเนาไว้ก่อนที่จะมีการดัดแปลงภาพ เช่น marked = img.copy() และดำเนินการเปลี่ยนค่าพิกเซลที่สำเนาแทน.
 |
 |
| ก | ข |
2.2.2.0.7 แบบฝึกหัด
จากค่าฟังก์ชัน \(g(\boldsymbol{v}) = -e^{-53-v_1^2 -2v_2^2-v_1 v_2 + 10 v_1 + 19 v_2}\) จงเขียนโปรแกรม เพื่อวาดภาพคอนทัวร์ และภาพสามทัศนมิติ ดังรูป [fig: opt 2D].
คำใบ้ คำสั่ง plt.contour จะวาดภาพคอนทัวร์ จากค่าพิกัดสามแกนมิติ ดังนั้นเพื่อจากวาดภาพคอนทัวร์ จะต้องคำนวณค่าฟังก์ชัน \(g\) ที่ \(v_1\) และ \(v_2\) ต่าง ๆ ทั้งหมดที่ครอบคลุมบริเวณที่จะวาด. ตัวอย่าง เช่น หากต้องการวาดครอบคลุมบริเวณ \(v_1\) มีค่า \(1\) ถึง \(5\) และ \(v_2\) มีค่า \(2\) ถึง \(6\) โดยวาดให้มีความละเอียดมิติละ \(40\) จุด จะต้องคำนวณค่า ฟังก์ชัน \(g\) ที่ \(v_1\) และ \(v_2\) ในบริเวณนี้ออกมา \(1600\) ค่า. คำสั่ง np.meshgrid อาจช่วยลดภาระการจับคู่ค่า \(v_1\) และ \(v_2\) ได้.
2.2.2.0.8 แบบฝึกหัด
จากปัญหามอนตี้ฮอล ในหัวข้อ [sec: prob cond prob examples] จงเขียนโปรแกรมเพื่อจำลองสถานการณ์ และแสดงให้เห็นว่า โอกาสที่ผู้เข้าแข่งขันจะได้รางวัล หากเลือกที่จะเปลี่ยนประตูเป็น \(2/3\) และโอกาสที่ผู้เข้าแข่งขันจะได้รางวัล หากเลือกประตูเดิมเป็น \(1/3\).
อภิปรายโปรแกรม และผลการทดลอง พร้อมออกแบบวิธีนำเสนอผล ให้ประจักษ์ชัดเจน. รูป 6 แสดงตัวอย่างวิธีนำเสนอผล ซึ่งจากรูปจะเห็นว่า เมื่อจำนวนซ้ำมากขึ้น โอกาสที่จะชนะเมื่อเลือกประตูเดิม (ภาพกลาง) จะประมาณ \(0.33\) หรือ \(1/3\) ในขณะที่ ถ้าเปลี่ยนไปประตูใหม่ โอกาสจะประมาณ \(0.67\) หรือ \(2/3\).
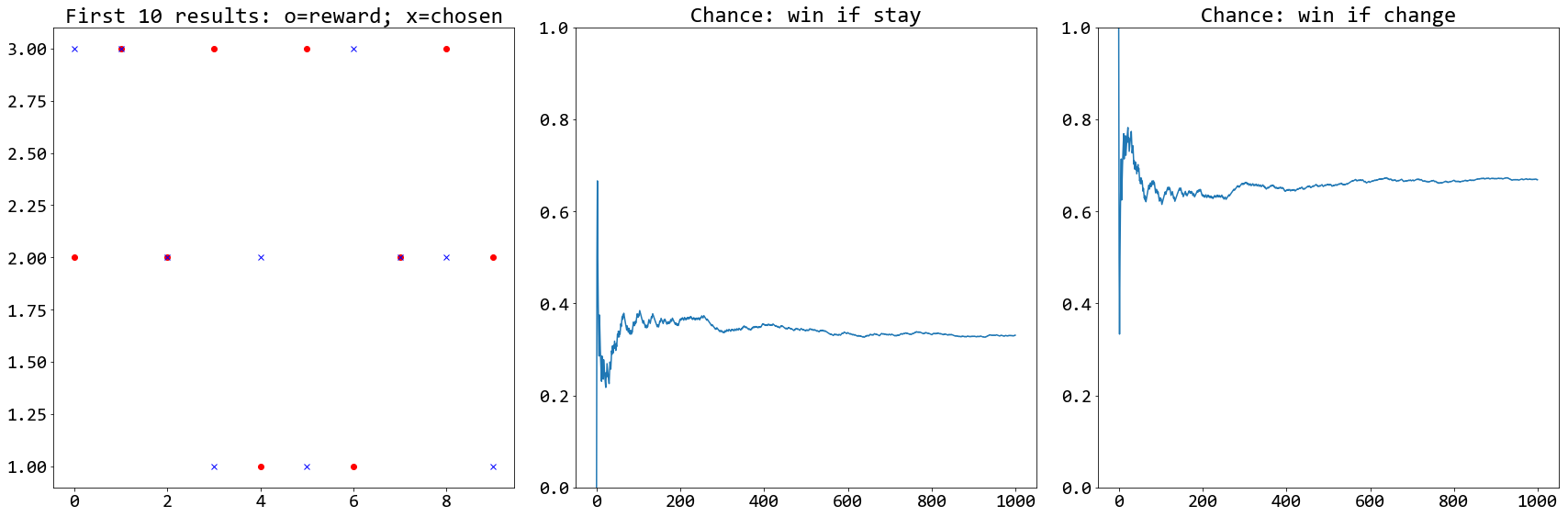
คำใบ้ คำสั่ง np.random.choice ใช้สุ่มเลือกค่าจากลิสต์. รางวัลอาจสุ่มให้อยู่ประตูไหนก็ได้. ประตูที่ผู้เข้าแข่งขันเลือก ก็อาจอยู่ประตูไหนก็ได้. แต่ประตูที่พิธีกรเลือกเปิด จะเป็นประตูที่มีรางวัลไม่ได้ หรือจะเป็นประตูที่ผู้แข่งขันเลือกก็ไม่ได้. การเลือกประตูของพิธีกร ต้องทำหลังจากการเลือกประตูรางวัล และการเลือกประตูของผู้แข่งขัน.
2.2.2.0.9 แบบฝึกหัด
ผลการคำนวณค่าสถิติจากข้อมูลที่จำกัด จะมีความไม่แน่นอนอยู่ 1 ในแง่ที่ว่า หากสุ่มกลุ่มข้อมูลออกมาใหม่ แล้วผลการคำนวณอาจจะเปลี่ยนไป.
หากคำนวณค่าเฉลี่ยของกลุ่มข้อมูลที่สุ่มมาจากการแจกแจงเดียวกัน และนำค่าเฉลี่ยของแต่ละการสุ่มมาวิเคราะห์ จะพบว่า ค่าเบี่ยงเบนมาตราฐานของค่าเฉลี่ย \[\begin{eqnarray} \mathrm{SD}(\mu_N) = \sqrt{\mathrm{var}\left[ \frac{1}{N} \sum_{n=1}^N x_n \right]} = \frac{\sigma}{\sqrt{N}} \label{eq: standard error} \end{eqnarray}\] เมื่อ \(\mu_N\) คือค่าเฉลี่ยที่ของกลุ่มขนาด \(N\) และ \(x_n\) คือจุดข้อมูลในกลุ่มที่สุ่มขึ้นมา และ \(\sigma\) คือ ค่าเบี่ยงเบนมาตราฐานของการแจกแจง.
จากทฤษฎีข้างต้น ยิ่งกลุ่มข้อมูลมีขนาดใหญ่ (\(N\) มีค่ามาก) ค่าเฉลี่ยที่คำนวณได้จะยิ่งมีความแม่นยำใกล้เคียงกับค่าเฉลี่ยจริงของการแจกแจงเท่านั้น.
จงเขียนโปรแกรม เพื่อแสดงในเห็นว่า สมการ \(\eqref{eq: standard error}\) เป็นจริง.
ตัวอย่างการนำเสนอ แสดงในรูป 7. (ไม่จำเป็นต้องทำตามตัวอย่างนี้.) ผลที่ได้ มาจากการจำลอง (simulation) โดย กำหนดการแจกแจงแบบเกาส์เซียน ที่มีค่าเฉลี่ยเป็นศูนย์ และค่าความแปรปรวน \(\sigma^2\) และจำลองการสุ่มกลุ่มจำนวน \(N\) ขึ้นมา. ตัวอย่างนี้ ทดลองค่า \(\sigma\) สามค่าได้แก่ \(0.2\), \(1.0\), และ \(5.0\) แสดงด้วย ภาพซ้าย กลาง และขวา ตามลำดับ.
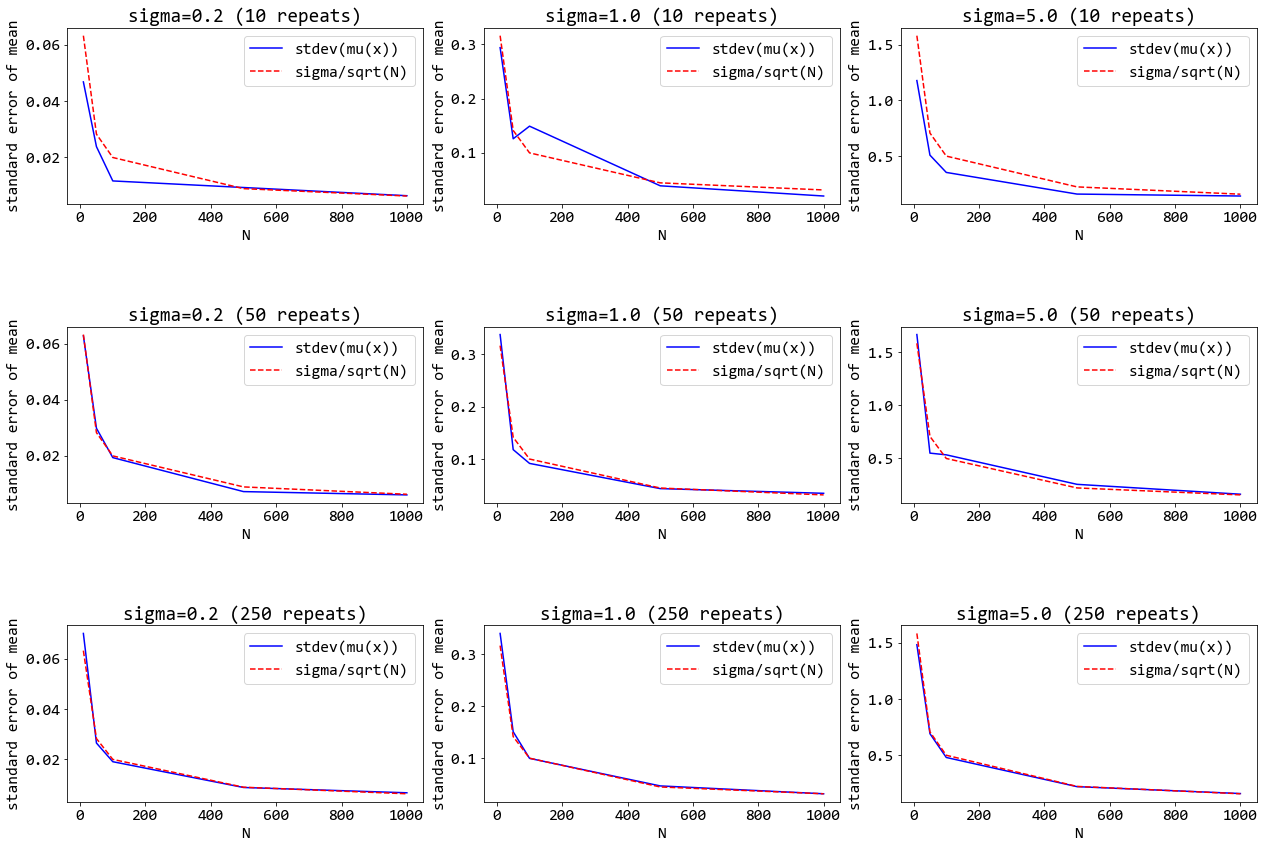
จากนั้น คำนวณค่า \(\mu_N\) ของกลุ่ม โดยทำซ้ำ \(10\) ครั้ง (ผลแสดงในภาพต่าง ๆ แถวบน) ทำซ้ำ \(50\) ครั้ง (แถวกลาง) และทำซ้ำ \(250\) ครั้ง (แถวล่าง). ค่าเฉลี่ยของแต่ละซ้ำจะถูกนำมาคำนวณค่าเบี่ยงเบนมาตราฐาน. นั่นคือ \(\widehat{\mathrm{SE}} = \sqrt{\frac{\sum_{r=1}^R m_r - \bar{m}}{R - 1} }\) เมื่อ \(\widehat{\mathrm{SE}}\) คือค่าเบี่ยงเบนมาตราฐานของค่าเฉลี่ย และ \(R\) คือ จำนวนซ้ำ. ส่วน \(m_r = \frac{1}{N} \sum_{n=1}^N x_n\) คือ ค่าเฉลี่ยของกลุ่มของซ้ำที่ \(r^{th}\) และ \(\bar{m} = \frac{1}{R} \sum_{r=1}^R m_r\). ค่า \(\widehat{\mathrm{SE}}\) (แทนด้วย เส้นทึบสีน้ำเงิน และสัญกรณ์ stdev(mu(x)) ในภาพ) เป็นค่าที่คำนวณจากข้อมูล ส่วน \(\sigma/N\) เป็นค่าที่คำนวณจากทฤษฎี (แทนด้วย เส้นประสีแดง และสัญกรณ์ sigma/sqrt(N) ในภาพ). ในแต่ละภาพ แกนตั้ง แสดงค่าเบี่ยงเบนมาตราฐานของค่าเฉลี่ย และแกนนอน แสดงค่าขนาดของกลุ่ม \(N\) ซึ่งในตัวอย่างใช้ \(10\), \(50\), \(100\), \(500\), และ \(1000\).
ผลที่ได้ แสดงในเห็นว่า (1) เมื่อ \(N\) ขนาดใหญ่ขึ้น ค่าเบี่ยงเบนมาตราฐานของค่าเฉลี่ยมีค่าเล็กลง. (2) ถ้า \(\sigma\) ของการแจกแจง มีค่าใหญ่ ค่าเบี่ยงเบนมาตราฐานของค่าเฉลี่ย ก็จะมีค่าใหญ่ตามสัดส่วน. (3) ค่าเบี่ยงเบนมาตราฐานของค่าเฉลี่ย ที่ได้จากการคำนวณกับข้อมูล เป็นไปตามทฤษฎี และจะเห็นความสอดคล้องได้ชัดเจนมากขึ้น เมื่อจำนวนซ้ำเพิ่มขึ้น.
หมายเหตุ ในทางปฏิบัติ เราไม่รู้ค่า \(\sigma\) ของการแจกแจง. ดังนั้น การประเมินความคลาดเคลื่อนของการคำนวณ เมื่อกลุ่มข้อมูลมีขนาดจำกัด จะไม่สามารถทำได้สะดวกเช่นนี้. ในทางปฏิบัติ เราจะสามารถประเมินความคลาดเคลื่อน ต่อขนาดข้อมูลได้อย่างไร. หรือ ที่น่าสนใจกว่าคือคำถามว่า ทำอย่างไร เราถึงจะสามารถประเมิน ได้ว่าภาระกิจที่กำลังทำอยู่ ต้องการจำนวนข้อมูลเท่าไร. อภิปราย พร้อมให้เหตุผลประกอบ.
2.2.2.0.10 แบบฝึกหัด
จากตัวอย่างปัญหาค่าน้อยที่สุด \(\min_x f(x)\) เมื่อ \(f(x) = -e^{-(x-5)^2}\) ในหัวข้อ [sec: opt grad desc] เราสามารถนำวิธีลงเกรเดียนต์สามารถนำไปเขียนโปรแกรมได้ง่าย ๆ โดยเริ่มจาก เตรียมเกรเดียนต์ของฟังก์ชันจุดประสงค์. นั่นคือ \(\nabla f(x) = -e^{-(x-5)^2} \cdot (-2x + 10)\) และไพธอนฟังก์ชัน grad ดังแสดงในรหัสโปรแกรมข้างล่าง จะทำหน้าที่คำนวณเกรเดียนต์นี้
def grad(x):
return -np.exp(-(x - 5)**2) * (-2*x +10)และหลังจากมีเกรเดียนต์แล้ว โปรแกรมวิธีลงเกรเดียนต์ก็สามารถทำงานได้ ดังแสดงในรายการ [code: gd simple]. โปรแกรมเลือกใช้ค่าขนาดก้าว step_size เป็น \(0.5\) (ตัวแปร \(\alpha\) ในสมการ \(\eqref{eq: opt gd}\)) และใช้เงื่อนไขจบเป็นจำนวนรอบสูงสุด ซึ่งในที่นี้ใช้เป็น \(8\) รอบ ที่ระบุลงไปให้ลูปเลย ด้วย for i in range(8)
ค่าเริ่มต้นของตัวแปรตัดสินใจ เลือกกำหนดให้เป็น \(6.5\) ในบรรทัดที่สอง และคำสั่งในบรรทัดที่สี่ คือการคำนวณสมการ \(\eqref{eq: opt gd}\).
step_size = 0.5
x = 6.5
for i in range(8):
x = x - step_size * grad(x)
print('x = ', x, '; grad = ', grad(x))จากโปรแกรมนี้ ทดลองรัน และเปรียบผลลัพธ์ที่ได้กับตัวอย่าง
2.2.2.0.11 แบบฝึกหัด
การใช้งานวิธีลงเกรเดียนต์ในทางปฏิบัติ นิยมเพิ่มเงื่อนไขการจบ เพื่อให้สามารถเลือกจำนวนรอบสูงสุดไว้มาก ๆ ก่อน โดยไม่ต้องกังวลว่า จะเสียเวลารันโดยไม่จำเป็น (ดูแบบฝึกหัด 1.2.2.0.12 ประกอบ)
จากแบบฝึกหัด 1.2.2.0.10 โปรแกรมวิธีลงเกรเดียนต์ง่าย ๆ ที่แสดงในรายการ [code: gd simple] สามารถเพิ่มเงื่อนไขการจบเข้าไปได้ ดังแสดงในรายการ [code: gd term]. เงื่อนไขจำนวนรอบสูงสุด ควบคุมได้โดยผ่านตัวแปร Nmax. โปรแกรมตัวอย่างนี้ ใช้เงื่อนไขความคลาดเคลื่อนยินยอม วัดค่าผ่าน eps โดย ถ้า eps น้อยกว่าหรือเท่ากับค่าที่ยินยอมได้ ก็จะจบการคำนวณทันที. ค่าที่ยินยอมได้ (tolerance) กำหนดผ่าน tol.
step_size = 0.5
Nmax = 500
tol = 0.00001
x = 6.5
for i in range(Nmax):
x = x - step_size * grad(x)
print(i, ': x = ', x, '; grad = ', grad(x))
eps = np.abs(grad(x))
if eps <= tol:
print('Reach termination criteria.')
breakสังเกตว่า โปรแกรมนี้ มีการคำนวณที่ซ้ำซ้อนมาก ในแต่ละรอบ เช่น grad(x) มีการคำนวณค่าเดียวกันถึงสามครั้ง. ความซ้ำซ้อนนี้สามารถลดลงได้ โดยการเก็บค่าไว้ในตัวแปร เช่น
...
x = 6.5
gradx = grad(x)
for i in range(Nmax):
x = x - step_size * gradx
gradx = grad(x)
print(i, ': x = ', x, '; grad = ', gradx)
eps = np.abs(gradx)
if eps <= tol:
print('Reach termination criteria.')
breakโดย ... แทนโค้ดต่าง ๆ ที่ละไว้ ไม่ได้หมายถึงการพิมพ์จุดสามครั้งเข้าไปในโปรแกรม. ตัวแปร gradx ใช้เก็บค่าเกรเดียนต์ที่คำนวณไว้แล้ว และค่าเกรเดียนต์ที่คำสั่งปรับค่า x = x -step_size * gradx จะเป็นคนละค่ากับที่คำสั่ง print และที่กำหนดค่า eps ดังนั้นตำแหน่งของ gradx = grad(x) จึงต้องอยู่หลังการปรับค่า x และเพื่อให้รอบคำนวณแรกสามารถทำได้ จึงต้องมีคำสั่ง gradx = grad(x) อยู่ก่อนเข้าลูปด้วย.
จากโปรแกรมในรายการ [code: gd term] จงทดลองรัน และเปรียบเทียบผล แล้วทดลองเปลี่ยนค่า tol เป็นค่าอื่น ๆ เช่น 0, 1e-5, 1e-3.
คำถามเพิ่มเติม. ทำไมเงื่อนไขความคลาดเคลื่อน นั่นคือ eps <= tol ถึงเขียนด้วยการเปรียบเทียบน้อยกว่าหรือเท่ากับ ทดลองเปลี่ยนเป็นการเปรียบเทียบน้อยกว่า ได้แก่ eps < tol และทดลองค่า tol ต่าง ๆ อีกครั้ง สังเกตและอภิปรายผล
2.2.2.0.12 แบบฝึกหัด
จากแบบฝึกหัด 1.2.2.0.10 จงทดลองเปลี่ยนจุดเริ่มต้น (บรรทัดที่สอง) เป็นค่าต่าง ๆ เช่น \(4\), \(5\), \(6\), \(7\), \(8\). ทดลองเพิ่มหรือลดจำนวนรอบสูงสุดถ้าจำเป็น ลองรันโปรแกรมในรายการ [code: gd simple] ใหม่ แล้วสังเกตผลที่ได้ ว่าที่ค่าเริ่มต้นต่าง ๆ ต้องคำนวณกี่รอบ ถึงจะได้คำตอบ เช่น จากตัวอย่าง ถ้าใช้ x = 6.5 จะได้คำตอบที่รอบที่เจ็ด (ให้ใช้ค่าขนาดก้าวเท่ากันหมดเป็น \(0.5\) ก่อน)
อภิปรายถึงประเด็นปัญหาที่จะเกิด เมื่อนำโปรแกรมนี้ไปรันในทางปฏิบัติ แล้วทำการทดลองใหม่ โดยรันโปรแกรมในรายการ [code: gd term] และอภิปรายข้อดีของการใช้เงื่อนไขการจบ ที่มีในโปรแกรม [code: gd term].
2.2.2.0.13 แบบฝึกหัด
เงื่อนไขความคลาดเคลื่อนยินยอม จะกำหนดค่าความคลาดเคลื่อนที่ยอมรับได้ ซึ่งอาจทำได้หลายวิธี เช่น ใช้ค่าความคลาดเคลื่อนของตัวแปร \(\epsilon_{\boldsymbol{v}} = \|\boldsymbol{v}^{(k+1)} - \boldsymbol{v}^{(k)}\|\) ใช้ค่าความคลาดเคลื่อนของเกรเดียนต์ \(\epsilon_{\nabla} = \|\nabla g(\boldsymbol{v}^{(k+1)}) - \nabla g(\boldsymbol{v}^{(k)})\|\) หรือใช้ค่าความคลาดเคลื่อนของฟังก์ชันจุดประสงค์ \(\epsilon_g = | g(\boldsymbol{v}^{(k+1)}) - g(\boldsymbol{v}^{(k)})|\) หรือใช้ค่าความคลาดเคลื่อนข้างต้นผสมกัน. อภิปรายเงื่อนไขความคลาดเคลื่อนยินยอมแต่ละแบบ คำใบ้ พิจารณาสมการ \(\eqref{eq: opt gd}\) และความหมายของเกรเดียนต์.
2.2.2.0.14 แบบฝึกหัด
จากตัวอย่าง ปัญหาค่าน้อยที่สุด เมื่อตัวแปรตัดสินใจเป็นเวกเตอร์ \(\min_{\boldsymbol{v}} \; g\) เมื่อ \(\boldsymbol{v} =[v_1, v_2]^T\) และ \(g(\boldsymbol{v}) = -e^{-53-v_1^2 -2v_2^2-v_1 v_2 + 10 v_1 + 19 v_2}\). คล้ายกับแบบฝึกหัด 1.2.2.0.10 วิธีลงเกรเดียนต์ต้องการฟังก์ชันคำนวณค่าเกรเดียนต์ ซึ่งอาจทำได้โดย
def grad(u):
assert type(u) == type(np.array([]))
assert u.shape == (2,1)
gu = g(u)
gradu = gu * np.array([[-2*u[0,0] - u[1,0] + 10],
[-4*u[1,0] - u[0,0] + 19]])
return graduฟังก์ชัน grad นี้ใช้คำสั่ง assert เพื่อจำกัดชนิดของอินพุต u เพื่อป้องกันปัญหาจากชนิดข้อมูล. ตัวแปร u แทนเวกเตอร์ \(\boldsymbol{u} = [u_1, u_2]^T\). ค่าส่วนประกอบ \(u_1\) และ \(u_2\) เข้าถึงได้โดย u[0,0] และ u[1,0] ตามลำดับ. นอกจากนี้ ฟังก์ชัน grad ยังเรียกใช้ฟังก์ชันจุดประสงค์ ซึ่งเขียนได้ดังนี้
def g(u):
assert type(u) == type(np.array([]))
assert u.shape == (2, 1)
loss = -np.exp(-53 - u[0,0] ** 2 - 2 * u[1,0] ** 2 - u[0,0] * u[1,0]
+ 10 * u[0,0] + 19 * u[1,0])
return lossรายการ [code: gd vec] แสดงตัวอย่างโปรแกรม วิธีลงเกรเดียนต์ เมื่อตัวแปรเป็นเวกเตอร์.
step_size = 0.4
Nmax = 1000
tol = 1e-6
v = np.array([[2.5], [3.5]])
losses = []
gradv = grad(v)
for i in range(Nmax):
v = v - step_size * gradv
gradv = grad(v)
loss = g(v)
losses.append(loss)
eps = np.linalg.norm(gradv)
if eps <= tol:
print('Reach termination at i={} with {}'.format(i, eps))
break
print('{}: v = [{:.3f} {:.3f}]; grad = [{:.4f} {:.4f}]'.format(i,v[0,0],v[1,0],gradv[0,0],gradv[1,0]))
print('{}: v = [{} {}]; g = {}'.format(i,v[0,0],v[1,0], loss))สังเกตว่า โปรแกรมบันทึกค่าฟังก์ชันจุดประสงค์ หรือเรียกว่าย่อ ๆ ว่า ค่าสูญเสีย (loss) ของทุกรอบการคำนวณไว้ใน losses. ค่าสูญเสียต่อรอบคำนวณ สามารถนำมาใช้ เพื่อตรวจสอบการทำงานแก้ปัญหาค่าน้อยที่สุดได้ ดังแสดงในภาพขวาบนของรูป [fig: opt gd 2D]. ภาพอื่น ๆ ในรูป [fig: opt gd 2D] ก็จะสามารถทำได้ในแบบเดียวกัน เพียงแต่ต้องบันทึกค่านั้น ๆ ขณะรันด้วย ซึ่งในที่นี้ ขอละไว้เพื่อไม่ให้โปรแกรมดูซับซ้อนเกินไป.
ลองเปรียบเทียบฟังก์ชัน grad กับการคำนวณหาค่าเกรเดียนต์ด้วยมือ และเปรียบเทียบโปรแกรมในรายการ [code: gd vec] เปรียบเทียบกับรายการ [code: gd term] และอภิปรายจุดแตกต่าง
ทดลองรันโปรแกรมในรายการ [code: gd vec] แล้วแก้ไขค่า step_size รัน และตรวจสอบผลที่ได้ กับการคำนวณของตัวอย่างในหัวข้อ [sec: opt contrained opt].
2.2.2.0.15 แบบฝึกหัด
จากปัญหาในแบบฝึกหัด 1.2.2.0.14 ทดลอง เปลี่ยนค่าขนาดก้าว (ตัวแปร step_size) ต่าง ๆ เช่น \(0.1\), \(0.2\), \(0.4\), \(0.8\) แล้วสังเกตผลและอภิปราย และเตรียมหลักฐานเพื่อประกอบการอภิปราย เช่น รูป 8 รูป 9 และรูป 10. ทดลองค่าอภิมานพารามิเตอร์อื่น ๆ เพื่อยืนยันข้อสรุปที่ได้อภิปราย.
รูป 8 แสดงความก้าวหน้าของการแก้ปัญหา (ค่าสูญเสียต่อรอบคำนวณ) เมื่อใช้ค่าขนาดก้าวต่าง ๆ (ตามระบุเหนือภาพ) โดยค่าอภิมานพารามิเตอร์อื่น ๆ คือ ใช้จำนวนรอบสูงสุด \(1000\) รอบ ใช้ค่าตัวแปรตัดสินใจเริ่มต้นเป็น \([2.5,3.5]^T\) และใช้ค่าความคลาดเคลื่อนยินยอม เป็น \(10^{-6}\).

รูป 9 แสดงความก้าวหน้าของการแก้ปัญหา เมื่อใช้ค่าขนาดก้าวต่าง ๆ ในภาพเดียวกัน โดยค่าขนาดก้าวที่ใช้ระบุด้วยสัญลักษณ์ ดังแสดงในกรอบคำอธิบายสัญลักษณ์ (legend). ภาพซ้ายแสดงในช่วง \(80\) รอบคำนวณแรก (เมื่อใช้ขนาดก้าวบางค่า การคำนวณจบก่อน \(80\) รอบ). ภาพขวาแสดงในช่วง \(10\) รอบคำนวณแรก เพื่อให้เห็นชัดเจนว่าที่ค่าขนาดก้าวเท่าใดลู่เข้าสู่คำตอบได้เร็วที่สุด (ค่าสูญเสียลดลงต่ำสุด ในรอบคำนวณที่น้อยที่สุด หมายถึงการลู่เข้าสู่คำตอบได้เร็วที่สุด). ตัวอย่างนี้ จะเห็นว่าขนาดก้าว \(0.4\) ช่วยให้วิธีลงเกรเดียนต์ลู่เข้าเร็วที่สุด และขนาดก้าวที่น้อยลง มีผลให้ลู่เข้าช้าลง. แต่หากใช้ขนาดก้าวที่ใหญ่เกินไป (เช่น \(0.8\) ในตัวอย่างนี้) อาจทำให้วิธีลงเกรเดียนต์ไม่สามารถลู่เข้าสู่คำตอบได้. รูป 10 แสดงค่าของตัวแปรตัดสินใจ \(v_1\) และ \(v_2\) สังเกตว่า เมื่อใช้ขนาดก้าว \(0.1, 0.2, 0.4\) ค่าของตัวแปรตัดสินใจลู่เข้าสู่ค่า \(3\) และ \(4\) ตามลำดับ โดย เมื่อใช้ขนาดก้าว \(0.4\) ค่าของ \(v_1\) และ \(v_2\) มีการส่ายอยู่บ้างก่อนส่ายน้อยลงจนลู่เข้าสู่คำตอบ. แต่เมื่อใช้ขนาดก้าว \(0.8\) ค่าของ \(v_1\) และ \(v_2\) แสดงการส่ายต่อเนื่องไปจนครบ \(1000\) รอบฝึกโดยไม่มีแนวโน้มจะลู่เข้า ขนาดก้าว \(0.8\) เป็นขนาดก้าวที่ใหญ่เกินไปอย่างชัดเจน. อภิปราย พฤติกรรมนี้ พร้อมวาด เสนทางการหาคาทำใหนอยที่สุด (เช่นรูป [fig: opt gd 2D trajectory]) เพื่อประกอบการอภิปราย.
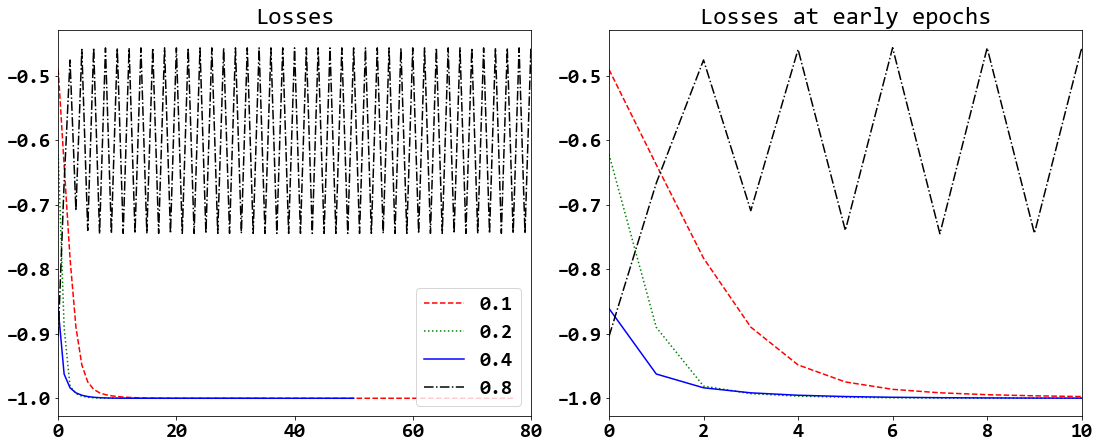
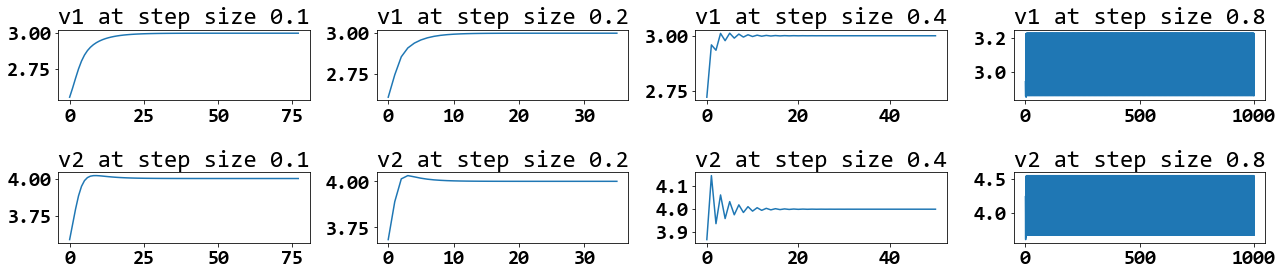
หมายเหตุ อย่างไรก็ตาม ค่าขนาดก้าวนี้ไม่จำเป็นต้องใช้เป็นค่าเดียวกันตลอดทุกรอบการคำนวณ อาจเปลี่ยนขนาดได้ตามความเหมาะสม เช่น อาจปรับให้ขนาดเล็กลง เมื่อจำนวนรอบคำนวณมาก ๆ ได้ หรืออาจใช้กลไกการปรับที่ซับซ้อนขึ้นได้ เช่น วิธีลงเกรเดียนต์ชันที่สุด (steepest gradient descent method ดู เพิ่มเติม สำหรับผู้ที่สนใจ).
2.2.2.0.16 แบบฝึกหัด
จงแก้ปัญหา \(\min_u \cos(2 \pi u - \frac{\pi}{4}) \cdot \exp \left( -\frac{u^2}{\pi}\right)\) ด้วยวิธีลงเกรเดียนต์.
ทดลองค่าเริ่มต้นต่าง ๆ เช่น \(-2, -1, -0.7, 0, 0.12301636938191951, 0.5, 1, 1.5\). เลือกค่าอภิมานพารามิเตอร์อื่น ๆ ให้เหมาะสม รันวิธีลงเกรเดียนต์จนสำเร็จ และสังเกตผลลัพธ์ที่ได้จากการใช้ค่าเริ่มต้นต่าง ๆ. อภิปรายความสัมพันธ์ระหว่างค่าเริ่มต้นต่าง ๆ กับผลลัพธ์ที่ได้. เมื่อใช้ค่าเริ่มต้นเป็น \(0.12301636938191951\) ผลลัพธ์เป็นอย่างไร ทำไมถึงเป็นเช่นนั้น?
รูป 11 แสดงค่าฟังก์ชันจุดประสงค์ \(g(u)\). อภิปรายการใช้งานวิธีลงเกรเดียนต์กับปัญหาลักษณะนี้ โดยเฉพาะในทางปฏิบัติ ที่มักไม่สามารถวาดกราฟของฟังก์ชันจุดประสงค์ได้.
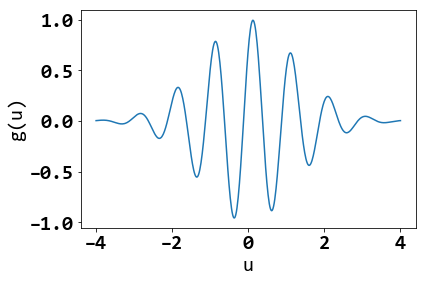
หมายเหตุ ปัญหาในแบบฝึกหัดนี้ จะเรียกว่า ปัญหาหลายภาวะ (multi-modal problem) ซึ่งคือ ปัญหาค่าน้อยที่สุดที่มีค่าทำน้อยที่สุดท้องถิ่นหลายที่ และวิธีลงเกรเดียนต์จะพบคำตอบที่ใกล้ที่สุด ที่ทิศทางเกรเดียนต์ของจุดเริ่มต้นชี้ไป เมื่อใช้ขนาดก้าวเล็กพอ.
2.2.2.0.17 แบบฝึกหัด
จงแก้ปัญหาของแบบฝึกหัด 1.2.2.0.16 โดยใช้การกำหนดค่าเริ่มต้นด้วยวิธีการสุ่ม แล้วทดลอง เพิ่มจำนวนทำซ้ำให้มากขึ้นเท่าตัว. สังเกตผลลัพธ์ที่ได้ อภิปรายว่า การกำหนดค่าเริ่มต้นด้วยวิธีการสุ่ม จะช่วยบรรเทาปัญหาของการติดอยู่ในสถานการณ์ที่ดีที่สุดท้องถิ่นได้อย่างไร
คำใบ้ ลองคำสั่งการสุ่มค่า เช่น คำสั่ง np.random.uniform, คำสั่งnp.random.normal, หรือคำสั่ง np.random.randn.
2.2.2.0.18 แบบฝึกหัด
จากแบบฝึกหัด 1.1.0.0.3 จงเขียนโปรแกรม เพื่อแก้ปัญหาแบบมีีข้อจำกัด และเปรียบเทียบผลที่ได้ กับผลที่แสดงในรูป 12. ผลที่แสดงในรูป 12 ได้จากการคำนวณวิธีลงเกรเดียนต์ โดยใช้ รอบคำนวณสูงสุด เป็น \(5000\) และใช้ค่าขนาดก้าวเป็น \(0.02\).
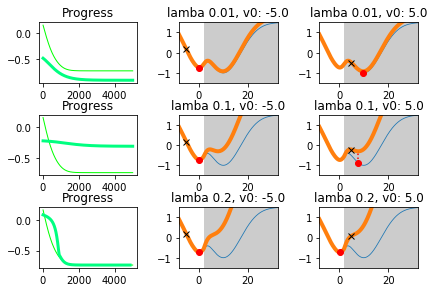
รูป 12 แสดงให้เห็นว่า เมื่อเลือกใช้ค่า \(\lambda\) ขนาดใหญ่มากพอ ไม่ว่าจะเลือกใช้ค่าเริ่มต้นที่ไหน คำตอบที่ได้จะเป็นค่าที่ใช้ได้ (feasible) ดังที่เห็นในแถวล่างสุด ภาพกลางและขวา.
2.2.2.0.19 แบบฝึกหัด
ทฤษฎีบทคารูชคุนทักเกอร์ (Karush-Kuhn-Tucker theorem คำย่อ KKT) 2 กล่าวถึงเงื่อนไขสำหรับค่าทำให้น้อยที่สุดของปัญหา \[\begin{eqnarray} \mathrm{minimize} & f(\boldsymbol{x}) & \nonumber \\ \mbox{subject to} & \boldsymbol{h}(\boldsymbol{x}) & = \boldsymbol{0}, \nonumber \\ & \boldsymbol{g}(\boldsymbol{x}) & \leq \boldsymbol{0}. \nonumber \end{eqnarray}\] เมื่อตัวแปร \(\boldsymbol{x} \in \mathbb{R}^n\). ฟังก์ชันจุดประสงค์ \(f: \mathbb{R}^n \mapsto \mathbb{R}\). ฟังก์ชันข้อจำกัด \(\boldsymbol{h}: \mathbb{R}^n \mapsto \mathbb{R}^m\), \(\boldsymbol{h} = [h_1, \ldots, h_m]^T\). และฟังก์ชันข้อจำกัด \(\boldsymbol{g}: \mathbb{R}^n \mapsto \mathbb{R}^p\), \(\boldsymbol{g} = [g_1, \ldots, g_p]^T\).
ทฤษฎีบทคารูชคุนทักเกอร์ กล่าวว่า หากกำหนดให้ฟังก์ชัน \(f\), \(\boldsymbol{h}\), และ \(\boldsymbol{g}\) เป็นฟังก์ชันที่สามารถหาอนุพันธ์ได้อย่างต่อเนื่อง (continuously differentiable) ซึ่งระบุด้วยสัญกรณ์ \(f, \boldsymbol{h}, \boldsymbol{g} \in \mathcal{C}^1\) และกำหนดให้ \(\boldsymbol{x}^\ast\) เป็นจุดปรกติ และเป็นค่าทำให้น้อยที่สุดท้องถิ่นของปัญหา \(\min f(\boldsymbol{x})\) \(\mbox{ s.t. }\) \(\boldsymbol{h}(\boldsymbol{x}) = \boldsymbol{0},\) \(\boldsymbol{g}(\boldsymbol{x}) \leq \boldsymbol{0}\) แล้วจะต้องมี \(\boldsymbol{\alpha} \in \mathbb{R}^m\) และ \(\boldsymbol{\beta} \in \mathbb{R}^p\) โดยที่
| (หนึ่ง) | \(\boldsymbol{\beta} \geq \boldsymbol{0}\), |
| (สอง) | \(\nabla f(\boldsymbol{x}^\ast) + \boldsymbol{\alpha}^{T} \nabla \boldsymbol{h}(\boldsymbol{x}^\ast) + \boldsymbol{\beta}^{T} \nabla \boldsymbol{g}(\boldsymbol{x}^\ast) = \boldsymbol{0}^T\), และ |
| (สาม) | \(\boldsymbol{\beta}^{T} \boldsymbol{g}(\boldsymbol{x}^\ast) = 0\). |
การประยุกต์ใช้ทฤษฎีบทคารูชคุนทักเกอร์ จะใช้เงื่อนไขทั้งสามนี้ ประกอบกับอีกสองเงื่อนไขข้อจำกัดเดิม ได้แก่ \(\boldsymbol{h}(\boldsymbol{x}^\ast) = \boldsymbol{0}\) และ \(\boldsymbol{g}(\boldsymbol{x}^\ast) \leq \boldsymbol{0}\) เพื่อค้นค่า \(\boldsymbol{x}\)’s ต่าง ๆ ที่มีโอกาสเป็นค่าทำให้น้อยที่สุด \(\boldsymbol{x}^\ast\).
หมายเหตุ จุดปรกติ (regular point) หมายถึง ค่า \(\boldsymbol{x}^\ast\) ที่สอดคล้องกับข้อจำกัดทั้งหมด และมีเกรเดียนต์ของข้อจำกัดที่ทำงานเป็นอิสระเชิงเส้นกัน. นั่นคือ ค่า \(\boldsymbol{x}^\ast\) จะเป็นจุดปรกติ เมื่อ เงื่อนไขดั้งเดิม \(h_1(\boldsymbol{x}^\ast) = 0\), \(\ldots\), \(h_m(\boldsymbol{x}^\ast) = 0\) และเงื่อนไขดั้งเดิม \(g_1(\boldsymbol{x}^\ast) \leq 0\), \(\ldots\), \(g_p(\boldsymbol{x}^\ast) \leq 0\) และเกรเดียนต์เวกเตอร์ \(\nabla h_i(\boldsymbol{x}^\ast)\), \(\nabla g_j(\boldsymbol{x}^\ast)\) สำหรับ \(i=1, \ldots, m\) และ \(j \in J(\boldsymbol{x}^\ast)\) เป็นอิสระเชิงเส้นต่อกัน โดย เซตของดัชนีข้อจำกัดที่ทำงาน \(J(\boldsymbol{x}^\ast) \equiv \{j : g_j(\boldsymbol{x}^\ast) = 0 \}\).
ข้อจำกัดแบบภาวะไม่เท่ากัน \(g_j(\boldsymbol{x}) \leq 0\) จะเรียกว่า ทำงาน (active) ที่ \(\boldsymbol{x}^\ast\) ถ้า \(g_j(\boldsymbol{x}^\ast) = 0\) และข้อจำกัด จะเรียกว่า ไม่ทำงาน (inactive) ที่ \(\boldsymbol{x}^\ast\) ถ้า \(g_j(\boldsymbol{x}^\ast) < 0\).
ความหมายของทฤษฎีบทคารูชคุนทักเกอร์ คือ ด้วยเงื่อนไข \(\beta_j \geq 0\) และข้อจำกัด \(g_j(\boldsymbol{x}^\ast) \leq 0\) ทำให้เงื่อนไข \(\boldsymbol{\beta}^T \boldsymbol{g}(\boldsymbol{x}^\ast) = \beta_1 g_1(\boldsymbol{x}^\ast) + \ldots + \beta_p g_p(\boldsymbol{x}^\ast)\) สามารถอนุมานได้ว่า ถ้า \(g_j(\boldsymbol{x}^\ast) < 0\) แล้ว \(\beta_j = 0\) แต่ถ้า \(g_j(\boldsymbol{x}^\ast) = 0\) แล้ว \(\beta_j\) อาจจะมีค่าเป็นบวกก็ได้ หรือเป็นศูนย์ก็ได้.
จงวิเคราะห์ค่า \(\boldsymbol{x}^\ast\) ด้วยเงื่อนไขจากทฤษฎีบทคารูชคุนทักเกอร์ สำหรับปัญหา \(\min f(\boldsymbol{x})\) s.t. \(\boldsymbol{g}(\boldsymbol{x}) \leq 0\) โดย \(g_1(\boldsymbol{x})= (x_1 - 1.5)^2 + x_2 - 5.5\) และ \(g_2(\boldsymbol{x}) = 0.2 x_1^2 - x_2 + 2.5 \leq 0\) และ \(f(\boldsymbol{x}) = 1.5 (x_1 + c_1)^2 + 1.5 (x_2 + c_2)^2\) เมื่อ
(สถานการณ์ ก) \(c_1 = 3.27\) และ \(c_2 = 4.8\).
(สถานการณ์ ข) \(c_1 = 3.27\) และ \(c_2 = 3.98950997289\).
(สถานการณ์ ค) \(c_1 = 2\) และ \(c_2 = 4\).
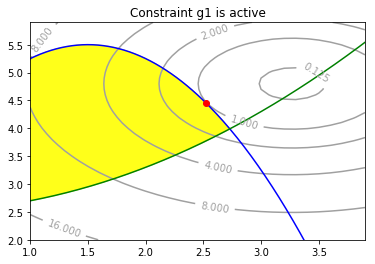
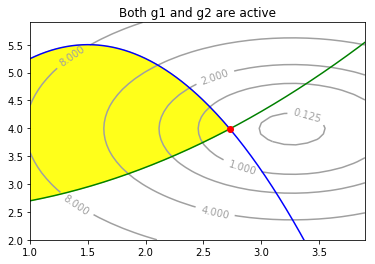
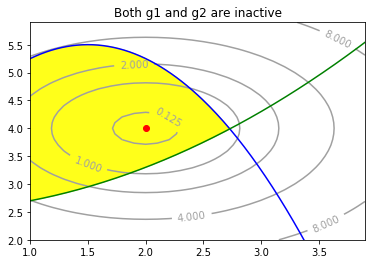
พร้อมเขียนโปรแกรม เพื่อแสดงผลเช่นรูป 15.
ตัวอย่างการตรวจสอบเงื่อนไขคารูชคุนทักเกอร์ พิจารณาสถานการณ์ ก เมื่อ \(f(\boldsymbol{x}) = 1.5 (x_1 + 3.27)^2 + 1.5 (x_2 + 4.8)^2\). จากเงื่อนไขที่หนึ่ง \(\beta_1 \leq 0\) และ \(\beta_2 \leq 0\). เงื่อนไขที่สอง \(\nabla f(\boldsymbol{x}) + \beta_1 \nabla g_1(\boldsymbol{x}) + \beta_2 \nabla g_2(\boldsymbol{x}) = 0\). นั่นคือ \[\begin{bmatrix} 3(x_1 - 3.27) + 2 \beta_1 (x_1 - 1.5) + 0.4 \beta_2 x_1 \\ 3(x_2 - 4.8) + \beta_1 - \beta_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\] และเงื่อนไขที่สาม \(\beta_1 g_1(\boldsymbol{x}) + \beta_2 g_2(\boldsymbol{x}) = 0\). นั่นคือ \(\beta_1 (x_2 + (x_1 - 1.5)^2 - 5.5) + \beta_2 (-x_2 + 0.2 x_1^2 + 2.5) = 0\).
กรณีแรก (a) ถ้า \(\beta_1 = \beta_2 =0\). เมื่อแทนค่า \(\beta_1\) และ \(\beta_2\) เข้าไปในเงื่อนไขที่สองแล้วจะได้ว่า \(\boldsymbol{x}_a = [3.27, 4.8]^T\) แต่เมื่อตรวจสอบเงื่อนข้อจำกัด \(g_1(\boldsymbol{x}_a) = 2.4329\) ซึ่งละเมิดข้อจำกัด \(g_1(\boldsymbol{x}) \leq 0\). ดังนั้น \(\boldsymbol{x}_a\) ไม่ใช่คำตอบ.
กรณีที่สอง (b) ถ้า \(\beta_1 = 0\). เมื่อแทนค่า \(\beta_1\) เข้าไปในเงื่อนไขที่สองและเงื่อนไขที่สาม จะได้สามสมการ ซึ่งสามารถแก้สมการเพื่อหาค่า \(x_1, x_2, \beta_2\) ออกมาได้ หลังจากแก้สมการแล้ว จะได้ \(\boldsymbol{x}_b = [3.348, 4.742]^T\) และ \(\beta_2 = -0.175\) ซึ่งค่า \(\beta_2 < 0\) ละเมิดเงื่อนไขแรก. ดังนั้น \(\boldsymbol{x}_b\) ไม่ใช่คำตอบ.
กรณีที่สาม (c) ถ้า \(\beta_2 = 0\). เมื่อแทนค่า \(\beta_2\) เข้าไปในเงื่อนไขที่สองและเงื่อนไขที่สาม จะได้สามสมการ ซึ่งสามารถแก้สมการเพื่อหาค่า \(x_1, x_2, \beta_2\) ออกมาได้ หลังจากแก้สมการแล้ว จะได้ \(\boldsymbol{x}_c = [2.529, 4.440]^T\) และ \(\beta_1 = 1.079\) ซึ่งค่า \(\beta_1 > 0\) สอดคล้องกับเงื่อนไขแรก และเมื่อตรวจสอบ \(g_1(\boldsymbol{x}_c) = 0\) และ \(g_2(\boldsymbol{x}_c) = -0.661\) ซึ่งก็สอดคล้องกับข้อจำกัด \(\boldsymbol{g}(\boldsymbol{x}) \leq \boldsymbol{0}\). ดังนั้น \(\boldsymbol{x}_c\) สามารถเป็นคำตอบได้.
 |
 |
 |
หมายเหตุ การแก้สมการด้วยมือ เป็นการฝึกทักษะที่ดี. แต่อย่างไรก็ตาม ไพธอนมีเครื่องมือที่สะดวกในการช่วยแก้สมการลักษณะแบบนี้. คำสั่งข้างล่างนี้ แสดงตัวอย่างการใช้ sympy เพื่อช่วยในการแก้สมการ (สถานการณ์ ก กรณี a)
from sympy.solvers import solve
from sympy import Symbol
x1, x2, beta2 = Symbol('x1'), Symbol('x2'), Symbol('beta2')
solve([3*(x1 - 3.27) + 0.4*beta2*x1,
3*(x2-4.8) - beta2,
beta2*(-x2 + 0.2*x1**2 + 2.5)])ในทางปฏิบัติ การแก้ปัญหาแบบมีีข้อจำกัด อาจจะสะดวกกว่าที่จะเลือกใช้วิธีการลงโทษ แต่ทฤษฎีบทคารูชคุนทักเกอร์ ช่วยให้ความเข้าใจเกี่ยวกับคำตอบของปัญหา ซึ่งในหลาย ๆ กรณี ได้นำไปสู่วิธีการแก้ปัญหาที่มีประสิทธิภาพมาก. (หัวข้อ [sec: SVM] อธิบายแบบจำลองจำแนกค่าทวิภาค ที่การพัฒนาใช้ประโยชน์จากทฤษฎีบทคารูชคุนทักเกอร์)
2.2.2.0.20 แบบฝึกหัด
จงเขียนโปรแกรม เพื่อแก้ปัญหาในแบบฝึกหัด 1.2.2.0.19 โดยใช้วิธีการลงโทษ.
คำใบ้ วิธีการลงโทษต้องการฟังก์ชันลงโทษ. ตัวอย่างเช่น ฟังก์ชันลงโทษ \(P_1(\boldsymbol{x})\) สำหรับข้อจำกัด \(g_1(\boldsymbol{x}) \leq 0\) อาจกำหนดเป็น \(P_1(\boldsymbol{x}) = \delta(g_1(\boldsymbol{x})) \cdot g_1(\boldsymbol{x})\) เมื่อ \(\delta\) เป็นฟังก์ชันขั้นบันไดหนึ่งหน่วย (unit step function). นั่นคือ \[\delta(a) = \left\{ \begin{array}{l l} 0 & \quad \mbox{เมื่อ} \quad a < 0, \\ 1 & \quad \mbox{เมื่อ} \quad a \geq 0. \end{array} \right.\]
คำสั่งข้างล่าง แสดงตัวอย่างโปรแกรมเกรเดียนต์ \(\nabla P_1(\boldsymbol{x})\) ของฟังก์ชันลงโทษ \(P_1(\boldsymbol{x})\).
def dPenalized_g1(x):
g1 = x[1,0] + (x[0,0] - 1.5)**2 - 5.5
dP = (g1 > 0) * np.array([[2*(x[0,0]-1.5)],[1]])
return dPสังเกต การเขียนโปรแกรมข้างต้นใช้กลไก (g1 > 0) ซึ่งเทีียบเท่า \((1 - \delta(-g_1))\). การใช้กลไกลักษณะนี้จะให้ค่าเป็นหนึ่ง (ลงโทษ) เมื่อ g1 มากกว่าศูนย์ และให้ค่าเป็นศูนย์ (ไม่มีการลงโทษ) เมื่อ g1 น้อยกว่าหรือเท่ากับศูนย์. เงื่อนไขที่ขอบ (ที่ g1 เท่ากับศูนย์) จะไม่มีเกรเดียนต์. เมื่อเปรียบเทียบกับ (g1 >= 0) ซึ่งเทีียบเท่า \(\delta(g_1)\) ผลลัพธ์อาจต่างกันเพียงเล็กน้อย แต่การรวมเงื่อนไขขอบที่ถูกต้องอาจช่วยให้การทำงานของวิธีลงเกรเดียนต์มีเสถียรภาพมากขึ้น.
หมายเหตุ ปัญหาในแบบฝึกหัด 1.2.2.0.19 มีสองข้อจำกัด แต่ที่นี้แสดงตัวอย่างแค่สำหรับ \(g_1(\boldsymbol{x}) \leq 0\).
2.2.2.0.21 แบบฝึกหัด
หลาย ๆ สถานการณ์พบว่า ปัญหาการหาค่าดีที่สุดแบบมีเงื่อนไข จะมีคู่ปัญหาของมัน. และในกรณีนั้น ปัญหาการหาค่าดีที่สุดแบบมีเงื่อนไขดั้งเดิม จะเรียกว่า ปัญหาปฐม (primal problem) ส่วนปัญหาที่เป็นคู่ของปัญหาปฐม จะเรียกว่า ปัญหาคู่ (dual problem).
สำหรับตัวอย่างของภาวะคู่กัน (duality) พิจารณาปัญหาเชิงเส้นที่เขียนในรูป \[\begin{eqnarray} \underset{\boldsymbol{x}}{\mathrm{minimize}} & \boldsymbol{c}^T \boldsymbol{x} & \nonumber \\ \mbox{subject to} & \boldsymbol{A} \boldsymbol{x} & \geq \boldsymbol{b}, \nonumber \\ & \boldsymbol{x} & \geq \boldsymbol{0}. \nonumber \end{eqnarray}\] ฟังก์ชันจุดประสงค์ \(f(\boldsymbol{x}) = \boldsymbol{c}^T \boldsymbol{x}\) เป็นฟังก์ชันเชิงเส้น และข้อจำกัดต่าง ๆ ก็เป็นฟังก์ชันเชิงเส้น. การหาค่าดีที่สุดแบบมีเงื่อนไข สำหรับปัญหาเชิงเส้น มักถูกอ้างถึงด้วยชื่อ การโปรแกรมเชิงเส้น (linear programming). การโปรแกรมเชิงเส้น เป็นการศึกษาถึงขั้นตอนวิธีต่าง ๆ ที่มีประสิทธิภาพ สำหรับการหาค่าดีที่สุดแบบมีเงื่อนไข เพื่อใช้กับปัญหาเชิงเส้น. รายละเอียดของการโปรแกรมเชิงเส้น สามารถศึกษาเพิ่มเติมได้จาก หรือ .
จากวิธีลากรานจ์ (Lagrange method ศึกษาได้จาก ) ปัญหาเชิงเส้นแบบมีข้อจำกัดข้างต้น สามารถเขียนในรูปปัญหาที่ไม่มีข้อจำกัดได้เป็น \[\underset{\boldsymbol{x}}{\mathrm{min}} \quad \boldsymbol{c}^T \boldsymbol{x} - \boldsymbol{\lambda}_1^T (\boldsymbol{A} \boldsymbol{x} - \boldsymbol{b}) - \boldsymbol{\lambda}_2^T \boldsymbol{x}\] เมื่อ \(\boldsymbol{\lambda}_1 \geq \boldsymbol{0}\), \(\boldsymbol{\lambda}_1 \geq \boldsymbol{0}\), และทั้ง \(\boldsymbol{\lambda}_1\) กับ \(\boldsymbol{\lambda}_2\) มีค่าใหญ่มากพอ. สังเกตว่า หากมีการละเมิดข้อจำกัด เช่น \(\boldsymbol{A} \boldsymbol{x} < \boldsymbol{b}\) จะทำให้พจน์ \(- \boldsymbol{\lambda}_1^T (\boldsymbol{A} \boldsymbol{x} - \boldsymbol{b})\) มีค่าเป็นบวก และเมื่อประกอบกับกลไกของลากรานจ์พารามิเตอร์ \(\boldsymbol{\lambda}_1 \geq \boldsymbol{0}\) ที่หาก \(\boldsymbol{\lambda}_1\) มีขนาดใหญ่มากพอ จะทำให้ ค่าจุดประสงค์รวมมากขึ้น และส่งผลต่อเนื่องทำให้การค้นหาค่า \(\boldsymbol{x}\) จะต้องปรับค่า \(\boldsymbol{x}\) และส่งผลเป็นการแก้ไขการละเมิดดังกล่าว.
วิธีของวิธีลากรานจ์ จะต้องเลือกลากรานจ์พารามิเตอร์ให้เหมาะสม นั่นคือมีค่าใหญ่มากพอที่ข้อจำกัดจะไม่ถูกละเมิด. แต่การเลือกลากรานจ์พารามิเตอร์ที่มีค่าใหญ่มากเกินไป จะไปขัดขวางการค้นหาค่าที่ดีที่สุด (ผลลัพธ์ที่ได้ จะไม่ละเมิดข้อจำกัด แต่จะไม่ใช่ค่าที่ดีที่สุดที่เป็นไปได้ 3 ). ดังนั้น การเลือกขนาดของลากรานจ์พารามิเตอร์เอง ก็สามารถถูกมองเป็นปัญหาการหาค่าดีที่สุดได้. นั่นคือ เลือกขนาดของลากรานจ์พารามิเตอร์ที่ใหญ่ที่สุด ที่จะไม่ทำร้ายจุดประสงค์เดิมของปัญหาปฐม.
เพื่อความสะดวก กำหนดให้ฟังก์ชันจุดประสงค์รวม \[L \equiv \boldsymbol{c}^T \boldsymbol{x} - \boldsymbol{\lambda}_1^T (\boldsymbol{A} \boldsymbol{x} - \boldsymbol{b}) - \boldsymbol{\lambda}_2^T \boldsymbol{x}\] โดย \(\boldsymbol{\lambda}_1 \geq \boldsymbol{0}\) และ \(\boldsymbol{\lambda}_2 \geq \boldsymbol{0}\).
ดังนั้นเกรเดียนต์ \[\nabla_{\boldsymbol{x}} L = \boldsymbol{c}^T - \boldsymbol{\lambda}_1^T \boldsymbol{A} - \boldsymbol{\lambda}_2^T\] และเมื่อพิจารณา ณ จุดดีที่สุด 4 นั่นคือ ที่ \(\nabla_{\boldsymbol{x}} L = 0\) และแก้สมการจะได้ \(\boldsymbol{\lambda}_2^T = \boldsymbol{c}^T - \boldsymbol{\lambda}_1^T \boldsymbol{A}\). ดังนั้น ค่าฟังก์ชันจุดประสงค์รวม ณ จุดดีที่สุด (เมื่อแทนค่า \(\boldsymbol{\lambda}_2\) เข้าไป) จะเป็น \[L' = \boldsymbol{\lambda}_1^T \boldsymbol{b}\] โดย \(\boldsymbol{\lambda}_1 \geq \boldsymbol{0}\) และ \(\boldsymbol{\lambda}_2 \geq \boldsymbol{0}\). และ ณ จุดดีที่สุด เงื่อนไข \(\boldsymbol{\lambda}_2 \geq \boldsymbol{0}\) \(\equiv \boldsymbol{\lambda}_1^T \boldsymbol{A} \leq \boldsymbol{c}^T\). สังเกตว่า (1) \(L\) เป็นค่าฟังก์ชันจุดประสงค์รวม ที่ค่าขึ้นกับ \(\boldsymbol{x}\) แต่ \(L'\) เป็นค่าฟังก์ชันจุดประสงค์รวม ที่ได้เลือก \(\boldsymbol{x}\) ให้ดีที่สุดแล้ว และ (2) \(L'\) ไม่ใช่ฟังก์ชันของ \(\boldsymbol{x}\) แต่เป็นฟังก์ชันของ \(\boldsymbol{\lambda}_1\). การมองจากปัญหาจากมุมมองของ \(\boldsymbol{\lambda}_1\) จะทำให้ได้ปัญหาคู่ ซึ่งเขียนได้เป็น \[\begin{eqnarray} \underset{\boldsymbol{\lambda}_1}{\mathrm{maximize}} & \boldsymbol{\lambda}_1^T \boldsymbol{b} & \nonumber \\ \mbox{subject to} & \boldsymbol{\lambda}_1 & \geq \boldsymbol{0}, \nonumber \\ & \boldsymbol{\lambda}_1^T \boldsymbol{A} & \leq \boldsymbol{c}^T. \nonumber \end{eqnarray}\] สังเกต ข้อจำกัด \(\boldsymbol{\lambda}_1^T \boldsymbol{A} \leq \boldsymbol{c}^T\) เปรียบเสมือน เงื่อนไขที่ควบคุมไม่ให้ \(\boldsymbol{\lambda}_1\) มีค่าใหญ่เกินไปจนไปรบกวนจุุดประสงค์ดั้งเดิมในปัญหาปฐม.
หากเปรียบเทียบ ปัญหาปฐมเป็นเสมือนการหาค่า \(\boldsymbol{x}\) ที่ทำให้จุดประสงค์เดิมเล็กที่สุด แต่การดำเนินการให้จุดประสงค์เดิม \(f\) มีขนาดเล็ก ถูกควบคุมด้วยข้อจำกัดดั้งเดิมต่าง ๆ. ดังนั้น จุดประสงค์เดิมจะเล็กได้เท่าที่ข้อจำกัดเดิมอนุญาต. ในขณะที่ปัญหาคู่ มองจากอีกด้านของมุม มองจากจุดที่ปรับ \(\boldsymbol{x}\) ได้ดีที่สุดแล้ว แต่ต้องการคุมไม่ให้ละเมิดข้อจำกัด. ปัญหาคู่ จึงเสมือนการหาค่า \(\boldsymbol{\lambda}_1\) ที่ทำให้จุดประสงค์รวม \(L'\) (ซึ่งรวมข้อจำกัดเดิม และปรับ \(\boldsymbol{x}\) ดีที่สุดแล้ว) มีค่ามากที่สุด เพื่อรักษาข้อจำกัดเดิมต่าง ๆ ไว้ แต่การดำเนินการให้ \(L'\) ใหญ่ ถูกควบคุมไม่ให้มากเกินไปจนรบกวนจุุดประสงค์ดั้งเดิม.
เมื่อแก้ปัญหาคู่เสร็จ คำตอบจะได้ \(\boldsymbol{\lambda}_1^\ast\) และทำให้สามารถคำนวณ \(\boldsymbol{\lambda}_2^\ast = \boldsymbol{c} - \boldsymbol{A}^T \boldsymbol{\lambda}_1^\ast\). ด้วยความเชื่อมโยงและทฤษฎีบทคารูชคุนทักเกอร์ คำตอบของปัญหาปฐม สามารถพิจารณาได้ดังนี้. ตรวจดูส่วนประกอบต่าง ๆ นั่นคือ \(\boldsymbol{\lambda}_1^\ast = [\lambda_{11}, \ldots, \lambda_{1m}]^T\) และ \(\boldsymbol{\lambda}_2^\ast = [\lambda_{21}, \ldots, \lambda_{2n}]^T\). ถ้า \(\lambda_{1i} > 0\) แปลว่า เงื่อนไขที่ตำแหน่ง \(i^{th}\) ทำงาน นั่นคือ \(\boldsymbol{A}_{i,:} \cdot \boldsymbol{x} = b_i\). ถ้า \(\lambda_{2i} > 0\) แปลว่า \(x_i = 0\). ค่าของ \(\boldsymbol{x}^\ast\) สามารถวิเคราะห์ได้จากสมการที่ได้เหล่านี้.
ตัวอย่างปัญหาเชิงเส้นข้างล่าง \[\begin{eqnarray} \underset{x_1, x_2}{\mathrm{minimize}} & 2 x_2 - x_1 & \nonumber \\ \mbox{subject to} & -4 x_1 - x_2 & \geq -2, \nonumber \\ & x_1 & \geq 0, \nonumber \\ & x_2 & \geq 0. \nonumber \end{eqnarray}\] ซึ่งอยู่ในปฐมรูป (primal form). เปรียบเทียบกับแก้ปัญหา \[\begin{eqnarray} \underset{\lambda_1}{\mathrm{maximize}} & -2 \lambda_1 & \nonumber \\ \mbox{subject to} & \lambda_1 & \geq 0, \nonumber \\ & -4 \lambda_1 & \leq -1, \nonumber \\ & -\lambda_1 & \leq 2. \nonumber \end{eqnarray}\] ซึ่งเป็นรูปคู่ (dual form) ของปัญหาข้างต้น.
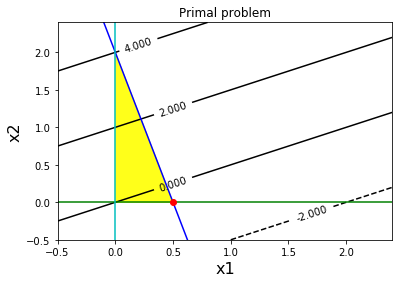
เมื่อแก้ปัญหาคู่เสร็จ ผลลัพธ์คือ \(\lambda_1^\ast = 0.25\). ดังนั้น \(\boldsymbol{\lambda}_2^\ast = [-1, 2]^T - [-4, -1]^T \cdot 0.25\) \(= [0, 2.25]^T\). เนื่องจาก \(\lambda_{22} > 0\) ดังนั้น \(x_2 = 0\). และเนื่องจาก \(\lambda_1 > 0\) ดังนั้น \(-4 x_1 - x_2 = -2\). เมื่อวิเคราะห์ผลทั้งหมดรวมกันจะได้ว่า \(\boldsymbol{x}^\ast = [0.5, 0]^T\). รูป 17 แสดงภาพของภาวะคู่กันในตัวอย่างนี้.
 |
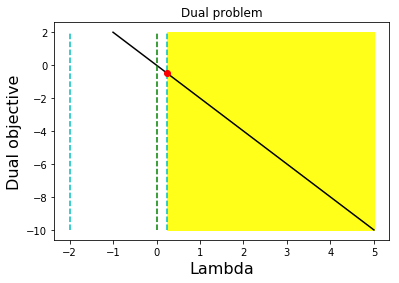 |
จากปัญหาเชิงเส้นข้างล่าง จงแปลงเป็นรูปคู่ แก้ปัญหาทั้งในรูปปฐม และรูปคู่ และตรวจสอบคำตอบ. \[\begin{eqnarray} \underset{x_1, x_2}{\mathrm{minimize}} & 2 x_2 + 2 x_1 & \nonumber \\ \mbox{subject to} & -4 x_1 - x_2 & \geq -2, \nonumber \\ & x_1 & \geq 0, \nonumber \\ & x_2 & \geq 0. \nonumber \end{eqnarray}\]
หมายเหตุ วิธีลงเกรเดียนต์ และวิธีลงโทษสามารถใช้ช่วยหาคำตอบได้ แต่ปัญหาเชิงเส้น เป็นกลุ่มปัญหาที่ได้รับการศึกษาอย่างกว้างขวาง และมีขั้นตอนวิธีต่าง ๆ ที่ได้พัฒนาขึ้นเฉพาะ ซึ่งมีประสิทธิภาพมากกว่าวิธีลงเกรเดียนต์มาก เช่น วิธีซิมเพล็กซ์ (simplex method) และวิธีจุดภายใน (interior-point method). เนื้อหาของปัญหาการหาค่าดีที่สุดสำหรับปัญหาเชิงเส้น เกินขอบเขตของหนังสือเล่มนี้ ผู้อ่านที่สนใจสามารถศึกษาเพิ่มเติมได้จาก .
2.2.3 การคำนวณเชิงเลข
การเขียนโปรแกรมคำนวณเชิงเลข มีปัจจัยด้านข้อจำกัดที่ต้องคำนึงถึง. แบบฝึกหัดต่อไปนี้ แนะนำบางประเด็นที่ควรคำนึงถึง เวลานำทฤษฎีทางคณิตศาสตร์มาเขียนโปรแกรม.
2.2.3.0.1 แบบฝึกหัด
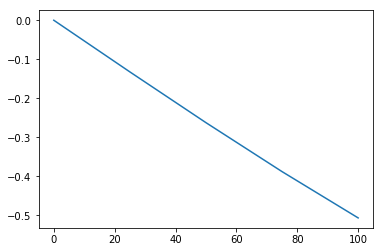
โปรแกรมข้างล่างนี้ใช้วาดรูป 18.
x = np.linspace(0, 100, 5)
plt.plot(x, np.sin(x))จงวิเคราะห์และอธิบายว่า ทำไมรูปที่ได้ไม่เห็นเป็นรูปโค้งขึ้นลง เช่น รูปของค่าพังชั่นไซน์ที่คุ้นเคย
2.2.3.0.2 แบบฝึกหัด
จากโปรแกรมและผลการรันดังแสดงข้างล่างนี้ จงอภิปรายว่าทำไมมี \(x\) บางตัวไม่เท่ากับ \(7 \cdot y\) ทั้ง ๆ ที่ \(y = x/7\). โปรแกรมคำนวณ
x = np.linspace(1,10, 20)
y = x/7
print(x == 7*y)และผลลัพธ์ที่ได้คือ
[ True True True True True True True True True True True True
True False False True True True True True]ทำไม จึงมีผลบางค่าที่เป็น False ทั้ง ๆ ที่ \(\frac{x}{7} \cdot 7\) มีค่าเท่ากับ \(x\) ? จงวิเคราะห์และอธิบายผลของ x == 7*(x/7) กับ x == 7*x/7 ประกอบ พร้อมอภิปรายประเด็นที่ได้เรียนรู้นี้ กับสถานการณ์ที่อาจจะเกิดขึ้น.
2.2.3.0.3 แบบฝึกหัด
จากคณิตศาสตร์ \(\log(\exp(x)) = x\) โปรแกรมข้างล่างนี้
xs = np.linspace(100, 800)
plt.plot(xs, xs/xs, 'r', linewidth=4)
plt.plot(xs, xs/np.log(np.exp(xs)), 'b', linewidth=1.5)วาดกราฟของ \(x/x\) เปรียบเทียบกับ \(x/\log(\exp(x))\) โดย \(x\) มีค่าตั้งแต่ \(100\) ถึง \(799\) ซึ่ง ทั้ง \(x/x\) และ \(x/\log(\exp(x))\) ก็มีค่าเท่ากับ \(1\) เมื่อ \(x > 0\). ดังนั้น ผลลัพธ์น่าจะเห็นเส้นตรงแนวนอนที่ค่าหนึ่ง เท่าเดิมคงที่ตลอดช่วง. แต่ผลที่ได้เป็นดังแสดงในรูป 19. จงสืบกรณีนี้ อธิบายสิ่งที่เกิดขึ้น และอภิปรายผลที่อาจเกิดขึ้นในทางปฏิบัติ จากประเด็นที่ได้เรียนรู้.
คำใบ้ ตรวจดูค่า np.exp(x) ที่ค่า x ต่าง ๆ และลองสืบค้นข้อมูลเรื่อง IEEE754 จากอินเตอร์เนต.

2.2.3.0.4 แบบฝึกหัด
ฟังก์ชันซอฟต์แมกซ์ (softmax function) ซึ่งมักใช้สัญลักษณ์ \(\mathrm{softmax}: \mathbb{R}^n \mapsto \mathbb{R}^n\) นิยามว่า เมื่อ อินพุตของซอฟต์แมกซ์ \(\boldsymbol{v} = [v_1, \ldots, v_n]^T\) แล้วผลลัพธ์ \(\boldsymbol{u} = \mathrm{softmax}(\boldsymbol{v})\) โดย \[\begin{eqnarray} u_i = \frac{\exp(v_i)}{\sum_{j=1}^n \exp(v_j)} \nonumber \end{eqnarray}\] สำหรับ \(i = 1, \ldots, n\) เมื่อ \(u_i\) เป็นส่วนประกอบของ \(\boldsymbol{u}\). ฟังก์ชันซอฟต์แมกซ์นิยมใช้อย่างมาก ในงานรู้จำรูปแบบ. โปรแกรมข้างล่างนี้ เขียนการคำนวณฟังก์ชันซอฟต์แมกซ์แบบง่าย ๆ
def softmax(v):
ev = np.exp(v)
return ev/np.sum(ev)จงทดสอบฟังก์ชันนี้ ด้วยค่า v ต่าง ๆ เช่น softmax(np.array([1, 2, 5])) (ลองผสมค่าหลาย ๆ แบบ ทั้งค่าบวก ค่าลบ และศูนย์) อภิปรายการพฤติกรรมของฟังก์ชันซอฟต์แมกซ์. แล้วลองทดสอบอีกครั้งด้วยค่าขนาดใหญ่ เช่น softmax(np.array([1000, 2000, 5000])) สังเกตผลลัพธ์ที่ได้ อภิปรายถึงปัญหาและสาเหตุ พร้อมเสนอวิธีแก้ปัญหา.
คำใบ้ ปัญหาอยู่ที่ไหน วิธีแก้อาจใช้คณิตศาสตร์ไปช่วยบรรเทาสาเหตุ. (หัวข้อ [sec: ann exercises] อภิปรายวิธีเขียนโปรแกรม ฟังก์ชันซอฟต์แมกซ์ที่ทนทาน (robust) สำหรับใช้งานในทางปฏิบัติ.)